Элементы теории графов

Федеральное агентство по образованию

Ярославский государс венный университет им. П. . Демидова

Êà åäðà òеоретической ин орматики

В. С. ублев

Элементы теории гра ов.

Изомор изм, планарность,

маршруты в гра ах

(ин и и у льны оты • 6 и 7 по исциплин

¾Îñíî û èñêð òíîé ì ò ì òèêè¿)

Ì òî è÷ ñêè óê íèÿ

мендовано

à

Научно-методическим советом

82

екомендовано

едакционно-издательским советом университета

в качестве учебного издания. План 2009/10 года

ка едра теоретической

ецензент

Ярославского государственного

университетин орматикиим. П. . Демидова

ублев, В. С. Элементы

гра ов. Изомор изм,

82

планарность, марш уты в гра ах: метод. указания

/ В. С. ублев; Яросл.

. унтеорииим. П. . Демидова. Яро-

славль: Яр У, 2010. 84гос.

ты индивидуаль

Методические ук зания содержат

íûõ

ïî

Изомор измварипл

арность гра ов ,

Маршруты в гра ах

плины Основы дискретн

ìà

заданий такжтемамнеобхдисц

ìûé

ÿ åå

ÿ

òåльного

âûï

лнения инд видуальных заданий.

Дляматикичеств,

íîãî óсвоения курсаматериалв здании данысамостоподр б

ые определизученияпримеры,ия,

иллюстрации

.

Предназначены для студентов,

обучающихобоснованияпо специаль-

ти 010400.62 Ин ормационные технологии (дисциплина

Îñновы дискретной математики , блок ЕН), очной ормы

обучения.

Ó

519.2

ÁÁÄÊ Â174ÿ73

Ярославский

государственный

университет

мноднозначноеÔóжеств. В общемсоотв

случае,твиеоответствкогданаиболеесоответствиепростыечастныйнебинарныеслучайяв етсяотношениявзаимноункцио

кциональноеэлемент может иметь много

íàãëÿäíîå åãî

ðåä

став ение гра . Представление отношенийобразов,виде

èñïîëü

нальнымзова еще Леонард Эйлер, но как наук

теория гра ов возникла в

30годы прошлого века с вых дом

моногра ии Кениггра Теорияов

ã à

êíèã

Êëî

Áåðæ

Теориякнигой,

ее приложения

ïåð âîäå

ïðî

ессора А.А. Зык

(п триарха ов

íà

ов . В оссии первой

посвященной этой теории, является

ÑÑÑ ),

изданнаяованач

1960-õ ãîä

. Îíà

чтения, äî-

статочное количество эк емпляров эт й книгипространствим етсдля библиотекбывшего

ßð Ó. Ñ òåõ ïîð áûëî

издано

оч нь много у ебников и моногра ий

Конечный гра (в последующемгра истовмин

конечный

всегда бу

теории гра ов как зарубежных,

àê

отечестве ных авторов.

из которых н

ÿ) G

определяетсмножеством вершин

гра а (каждый элемеет

ïî

êàê ïàðà

онечных мно

åñòâ, îä î

вершинадразумеватьсгр зываетса), другое

ÿ êàê

множество

(первого множ

называетсопределяетсмножеством ребер (к ждый эле

мент ребро,

соединяющее

2 вершины

. Таким обрпарзом,вершинîáî-

значении G(X;

ества)U X множество вершин,гра Uа) множество ребер (пар

вершин). Например,

; x

; x

g; ffx

; x

g; fx

; x

g; fx

; x

gg)

G(fx

; x

3

4

1

2

1

2

; x

1

3

3

4

гра , содержащий 4

x

1

; x

; x

4

и 3 ребра.

åî

етрически

2

3

ребра

ãðà à

зображаются точками,

линияìè,

ýòè ðøèíû-

. Ïðè ýòîì

неважно, где

располагаютссоединяющимивершинывершиныïер секаютсяточкиил не пересекаются ребра.

Íà ðèñ. 1 ïðиведены 3 изображения вышеприведенногî ãðà à G.

x

1

x

3

x

1

x

3

e

x

2

x

x

3

x

e

e

e

e

e 1

e

e 4

x

2

x

4

x

4

x

2

èñ. 1

3

вых элементов (вершин), то кажд я такая

изображ

я линией,

ëåéидущей, а соответствующийиз ршины ту ãðàæå

самуюгравершину,ом с петлямипарапотому. Примеромназываетсслужитя пет-

следующий гра G(fx

; x

; x

g; ffx

; x

g; fx

; x

gg);

1

2

3

1

2

2

2

содержащий 3 вершины и 2 рåáðà, одно из которых петля (см. рис. 2).

x

1

x

2

x

3

e

e

e

èñ. 2

Если в определении множества U ребер допуст ть повторяющиеся

элементы

то получим мультигра . Напрèìåð, ãðà

(ребра),G fy ; y

; y

g; ffy

1

; y

g; fy

; y

g; f

3

; y

g; fy

; y

gg)

1

2

3

2

2

3

2

2

3

содержит 3 ребра, соединяюùèõ âершины y

è y

3

(ñì. ðèñ. 3).

y

1

y

2

y

3

2

e

e

e

èñ. 3

Чаще всего мы будем рассматривать гра ы без петель

повторя-

а элеменòû

множества U называютсявляютсдугами. Наприядоченнымиер, оргра

ющих я ребер, которые называют обыкновенными гра ами.

Åñëè

ýëå åíòû ìíîæ òâà U

ÿ óïîð

èëè

парамиа о ,

вершин,

о гра называетñя ориентированным гра о

G(fy

; y

; y

g; f(y

; y

); (y

; y

); (y

; y

)g)

1

2

3

1

2

2

1

2

3

,

содержит 3 вершины

3 дуги, 2 из которых соединяют вершины y

y

2

è èäóò

разных

направлениях. В наглядном изображении

1

à ýòî

а, указывàþùàÿ íàïðавление от вершиныорграначала

äóãи к вершинестрелконца дуги (см. рис. 4).

y3

y1

y2

e

- e

- e

I

èñ. 4

4

шина x являетс

концом ребра u, то гов рят что x

u инциде тны

Вершины(вер ина x èнцидентнаy

ребруÿ êàêu, а реброìåæ ûåu , сли существуетвершинереброx).

fx; yg, связывающее эти вершины (инц дентноинцидентноэтим верши ам). Два

u

v являютсопределяютсмежными,

åñëè îíè

инцидентны од ой той

Степень вершины x определяется как число d(x) ребер,

инцидент-

ребраж вершèíå.

число вершин гра а G(X; U), а

ных x. Обозначим n(G) jXj

m(G) jUj ч ло ребер этого гра а.

Занумеруем

ñе ершины гра а X = fx ; x ; : : : ; x g. Число ребер

и степени вершин связаны следóющим соотношением

n

1

n

1

2

X

d(xi);

m = 2

i=1

åñëè ìû

åì

которое обосновывается следующим

раз, когда мы

ребро

степеобразом:дной из вершин,просуммирукот рой

степени всех вершин,

мы пересчитаем дважды каждое ребро (один

другой вершины, которой оно

î).

В оргра е дугучитываемимеет начало (вершина,

из которой она выхстепениодит)

áûòü äóãè,

выходящие из

инцидент

ÿùèå

вершину. По-

оно инцидент о,

âòî

раз, когда мы учитываем ребро

конец (вершина,

которую она вхо

ò). Â

с этим могут

èñ

(

) ê

соответствииисх дящих из вершины, и

полустепень захода d+(x) как

дуги,вх дящихвершинывершину.еделяют

этому вместо степени вершинывершины,оргра е для

îï

èëè

ж просуммировать все получислоуммироватьтепени зах да. Из этого следует со-

ñ÷

ать все дуги можно, если про

все полустепени исхПода

отношåíèå:

m =

n

n

Xd (xi) = Xd+(xi):

i=1

i=1

изолированной.

Еще несколько определений:

Âåðø

гра а, имеющая степень 0,1 называется

висячей.

ðà

называется полным, если любые 2 его вершины соединены

ребром,

и пустым, если все его вершины изолированы (множество ре-

5

На рис. 5 приведено изображениеx2 e x3ãðàe à K45.

ðà G(X; U)

1

èñ. 5

ex5

ÿ двудольным если мно ество X его вер-

øèí

жет быть разбитоназываетс 2 так х непересекающих я подмножества

(X = X

1

[ X

; X

1

\ X

2

= ;)

äîëè

гра а, что смежными

могут быть

2

; x

g 2 U

^ x

2 X

! x

X

.

толькмоверш

ны разных долей: fx

i

1

j

i

j

2

Íà ðèñ. 6 ïðèведен пример такого гра а с долями: X

1

= fx

; x ; x

g,

X2 = fx4; x5g.

1

ex4

1

2

3

2

x3

e èñ. 6

5

Полный двудольный гра это

дольный гра , у которого лю

бые 2 вершины, принадлежащие разным долям, смежны. Пол ый дву

ä

гра , имеющий n вершиндвупервой доле и m вершиí

âî âòî-

ð

льныйдоле (и потому n m ребер), обознач ется как K

.

если в гра , изображенный на рис. 6, добàвить ребро fx

;Например,x g то мы

получим

полный двудольный

K .

3

4

3;2

n;m

-äîëü ûé ãðà . Îí îïðå-

Обобщением двудольного гра аявляется

деляется разбиением множества вершин на n подмíожеств-долей:

X =

n

[Xi; Xk \ Xj = ; (k =6 j);

i=1

а также смежностью только вершин, принадлежащих соседним до-

ëÿì:

fx; yg 2 U; x 2 X

i

(1 < i < n)

! y 2 X

i+1

_ y 2 X

i 1

:

6

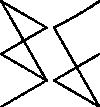
21

x4

76

x3

e

5

ex8

èñ.e7

2 Изомор изм гра ов и алгоритмические спосо-

бы задания гра а

Ñò óêòó

ãðà à

изменится, если переименовать его вершины

и ребра: х

ðàктеристики гра а, такие как количество вершин, коли

ребер, набор степеней

количество элеме тарных цик

честволов заданным

числом вершин

другие не зависят от

-

вершин ребер. Поэтому гра вершин,отличающиеся тольк

åì

вершин

ребер, будем назûâàòü

ìîð íûìè. Â òå ðèè ãðà û

учаются

точностью до

изомор изма. Дадим точноенаименованияпределение

èçî

îð èçìà

ãðà îâ.

(Y; V ) называются изомор ыми, если меж

ðà û G

(X; U) G

1

2

взаимно-

ду множествами их

вершин X и Y можно уста

однозначное соответствие ', сохраняющее смежность,овить. е. такое,

÷òî

8x

; x

j

2 X

fx

; x

g 2 U $ f'(x

); '(x

)g 2 V:

i

i

j

смежным в

i

j

ñîîò-

Таким образом при

ршинам гра а G

1

ветствуют смежные вершины гра а G

, несмежным

вершинам из

G

1

несмежные вершиныизомор измеG .

2

2

Пусть дан гра G(X; U). В силу изомор изма мы можем считать,

÷òî

ество

X = f1; 2; : : : ; ng. Таким образом, для зада

íèÿ

множества вершин

достаточно указать их число n. Множество

ребер можно задать сп

ском ребер как списком m пар номеров

. Ïðè ýòîì

безразличн ,

какой из номеров в паре будет первым,

íû первомk íå áõèëèä ìîвторомподсчитаìåñòüå.количествоТрудоемкостьïàð,такогов которыхалгоритмаk находитсяO(m).

Например, список f1; 2g; f1; 3g; f1; 4g; f2; 4g; f3; 4g

гра с 5 ребрами, где

пень вершины 3 равна 2. Если

определяетж каждое ребро

â ñïèñêå дважды

дин раз, когда од

из вершин стоит на

ðâîì ìå òå, à

второй

раз, к(огда другая

íà

на первом местопределить) этот писок упорядочить первой

вершине,

тогда для

степени

вершины необхподимо подсчит

к личество пар,определенияэта вершина стоит на пе вом месте. Трудоемкосòü

стоитакого алгоритма O(log m

+ max d(i)). Для примера,

написанного

выше, этот список выглядит следующим образом:

i

f1; 2g; f1; 3g; f1; 4g; f2; 1g; f2; 4g; f3; 1g; f3; 4g; f4; 1g; f4; 2g; f4; 3g:

Для оргра а порядок вершин в дуге риентирует ее и потому опре-

деляет порядок в паре. Например, списîê äóã

(1; 2); (1; 4); (2; 4); (3; 1); (4; 3)

ориентацией

определяет оргра с пятью дугами, которые

В случае неориенти ованного гра а

даполученыдобно задавать каж

ребер предыдущего гра а. d+ = 2; d = 1.

ое ребро

4

4

. Например, это упрощаетиног ускоряет алгоритм опре

äеления степени вершины.

Другойдваждыу бный способ задан я гра а G(X; U) матрица смеж-

элемент a

которой

равен 1, если вершиныматрицуi j смежны (есть ребро

ности вершин. Она представляет собой

A размерно

è n n,

ij

fi; jg), или 0, если не смежны (нет такого ребра).

aij

0; fi; jg 2= U:

= 1

М трица смеж ости обыкновенного гра а без петель имеет нулевую

главную диагональ

и является симметрической: aij = aji. В качестве

8

данного выше списком ребер:

0

73

62

4

1

0

0

1

5

1

1

0

Изображение этого гра а приведено на рис. 8.

2

e

1 e

e4

3

e

èñ. 8

ра с петлями имеет на диагонали единицы.

Эле енты матрицы смежности оргра а определяются следующим

образоì:

8

<

1

j; i

aij = :

0; (i; j) 2= U; (j; i) 2= U:

Матрица смежности оргра а является кососимметрической:

a

ji

= a

ij

:

В качестве примера приведем матрицу смежности оргра а, заданного

выше списком дуг:

2

0

1

1

3

6

7

4

1

0

0

1

5

1

1

0

1 eI

R-

e4

3

e

èñ. 9

межности вершин обык

В случае мультигра а элеме т матрицы

новенного гра а мож

иметь значение k, если k дуг связывают вер

Ещесоотведин способòñòвующиезаäàíèя гра а матрица инцидентности. Эле-

øèíû,

индексам элемент

матрицы.

ìåíò b

(i 2 1; n; j 2 1; m) матрицы инцидентности B определяется

ij

следующим образом:

инцидентна ребру j;

bij =

1

0; вершина i

не инцидентна ребру j:

В каждом столбце матрицы инцидентности имеются ровно 2 един цы,

ве шинам, которые являются концами ребра. Ч сло

соответствующиеединиц каждой ст оке

степень соответствующей

верши-

ны. В к честве примера

п ив дем матрицу инцидентности для гра а,

заданного

выше спискомопределяетебер:

0 3

2

1

1

1

0

6

0

0

1

7

0

1

1

4

5

я подобным образом.

Матрица инцидентности оргра а

bij = :

1

вершину i

определяетсвх дуга j;

8

из вершины i исх дит дуга j;

<

0;

В каждом

âершина i

инцидентна дуге j:

îâíî 1

столбце1 мину

ìàòð

û

инциден

ности

оргра а имеются

единица и

èöà,

соответствующие

ршинам, кото ые яв

дой строке определяет полустепеньонцамизах да соответствующей вершины,

ляются вых дящимединвх дящим к

дуги. Число единиц

êàæ-

10