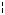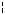Лабораторные работы по курсу общей физики
.pdf
3
Зависимость периода колебаний маятника от положения оси вращения
ивыражение момента инерции через период колебаний
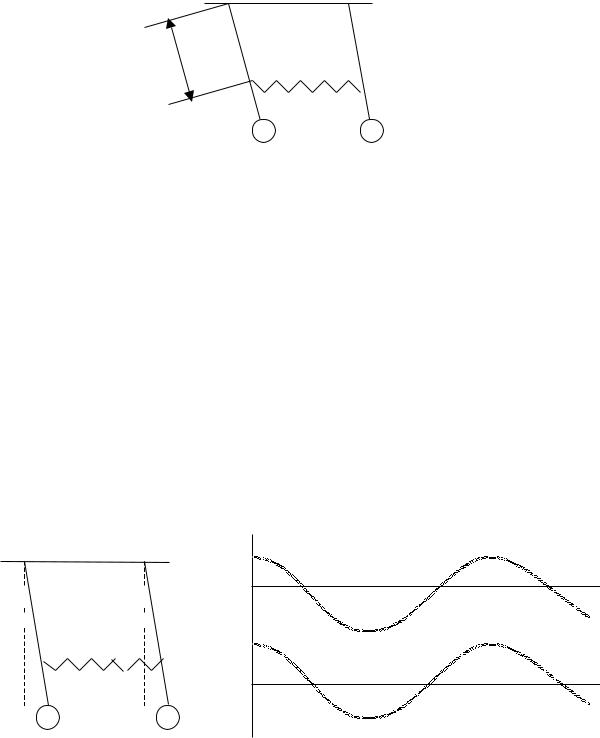
Всоответствии с теоремой Штейнера момент инерции маятника относительно произвольной оси равен моменту инерции относительно параллельной ей оси, проходящей через центр масс плюс произведение массы тела на квадрат расстояния между этими осями, т.е.
I = I0 + ma2
Формулу для периода колебаний теперь запишем в виде |
|
||||
T = 2π |
|
I0 |
+ ma2 |
|
( 7 ) |
|
mga |
||||
|
|
|
|
||
Зависимость периода T от расстояния a , |
т.е. функция T( a ), проходит через |
||||
минимум. Если взять от этой функции первую производную и приравнять ее нулю, то можно найти значение расстояния a , при котором период
минимален. Это расстояние |
a = |
|
|
I0 m |
. |
|
|
|
Подставив это значение a в формулу ( 7 ) , получим |
|
|||||||
|
|
|
|
|
|
|
|
|
Tmin |
= 2π |
4 |
|
4I0 |
. |
( 8 ) |
||
|
mg2 |
|||||||
|
|
|
|
|
|
|||
Если экспериментально определить Tmin , то момент инерции относительно оси , проходящей через центр масс I0 можно вычислить по формуле
I0 = |
mg 2 |
Tmin4 |
(9) |
|
64π 4 |
||||
|
|
|
полученной из выражения ( 8 ). Момент инерции относительно любой другой параллельной оси, смещенной на расстояние a , может быть найден по теореме Штейнера. Если положение центра масс неизвестно, то неизвестно и расстояние a . Тем не менее, момент инерции относительно произвольной оси можно найти и в этом случае, исходя из результатов измерения периода, пользуясь только одним измерительным прибором – секундомером.
Преобразуем формулу ( 7 ) к виду
a2 − |
gT 2 |
a + |
I0 |
= 0 |
( 10 ) |
|
8π 2 |
m |
|||||
|
|
|
|
Это квадратное уравнение, из которого можно определить параметр a , соответствующий измеренному значению периода T . Решение этого
уравнения имеет вид
a = |
|
g |
T 2 ± |
|
g2T 4 |
|
− |
I0 |
|
( 11 ) |
|||
8π 2 |
|
64π 4 |
m |
||||||||||
|
|
|
|
|
|
|
|||||||
С учетом формулы ( 8 ) можно также записать |
|
||||||||||||
a = |
g |
|
T 2 ± |
|
g |
|
|
|
( 12 ) |
||||
|
|
|
T 4 − T 4 |
||||||||||
8π |
2 |
8π 2 |
|||||||||||
|
|
|
|
|
|
min |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
||

5
через заостренные концы винтов 2. На стержне имеются риски, показывающие рекомендуемое расположение осей качания. Рядом с рисками расположены цифры, означающие номера осей. Ось, проходящая через заостренные концы винтов 2, должна совпадать с одной из рисок на стержне маятника.
Задание к работе
1.Измерить период колебаний маятника относительно каждой из предложенных осей. Период определить по формуле T = tn n , где tn - время
n |
колебаний, n -число колебаний . Для увеличения точности измерений |
|
n |
должно быть, по возможности, большим ( например, 100 колебаний ). |
|
2. |
Результаты измерений представить на графике. По вертикальной оси |
|
отложить значения T 4 , |
по горизонтальной – равномерно распределенные |
|
номера осей от 1 до N . |
Tmin4 и по формуле ( 9 ) найти I0 . |
|
3. По графику определить |
||
4. |
Определить момент инерции маятника относительно одной из осей по |
|
указанию преподавателя.
Контрольные вопросы
1.Какова цель работы ?
2.В каком случае при выводе дифференциального уравнения физического маятника потерями энергии можно пренебречь ?
3.Вывести это дифференциальное уравнение в указанном приближении.
4.Какими функциями, кроме приведенной в выражении (4), может описываться решение уравнения (3) ?
5.Как с помощью только одного измерительного прибора – секундомера ( при известной массе тела ) можно определить момент инерции тела ?
6.Формула (13) дает ( с учетом знаков ± внутри формулы ) два значения момента инерции. Как это понимать ? В каком случае использовать
формулу со знаком + , а в каком – со знаком - ?
7.
Литература
1.Трофимова Т.И. Курс физики. - М. : Высшая школа, 1997. - § 140, 141, 142.
2.Детлаф А.А. Яворский Б.М. Курс физики. – М. : Высшая школа , 1999. - § 27.1, 27.2.
3.Савельев И. В. Курс общей физики. – Кн.1.-М. : Наука, Физматлит, 1998. - § 8.5.
1
Лабораторная работа № 20б
СВОБОДНЫЕ КОЛЕБАНИЯ В СИСТЕМЕ ДВУХ СВЯЗАННЫХ МАЯТНИКОВ
Цель работы - в системе двух связанных физических маятников измерить
частоты нормальных колебаний и частоту биений при различной степени связи. Соотношение между частотами и зависимость этих частот от степени связи сравнить с теоретическими.
Гармонические колебания в системе с двумя степенями свободы (нормальные колебания)
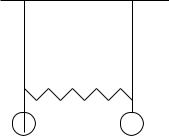
Экспериментальная установка (рис.1) состоит из двух одинаковых физических маятников, соединенных пружиной (П), измерительной шкалы (Ш) и секундомера. Маятники представляют собой стержни (С) с укрепленными на них чечевицами (Ч). Пружину можно перемещать вдоль стержней С. Этим обеспечивается изменение связи между маятниками.
ОО
С |
С |
П
Ч |
|
|
|
|
|
|
|
|
|
|
|
Ч |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ш
Рис. 1
Экспериментальная установка подставляет собой систему с двумя степенями свободы. Это значит, что для фиксирования (определения) положения системы в пространстве (т.е. положения обоих маятников) необходимо задать всего две какие-либо величины. Этими величинами могут быть ( xЛ , xП ) - горизонтальные смещения, или ( yЛ , yП ) –
вертикальные смещения, или (α Л ,α П ) - углы отклонения маятников и т.п.
(Индексы «Л» и «П» у величин указывают принадлежность величины левому или правому маятнику). Какие две величины взять – это в
3
Гармонические колебания также можно наблюдать, если отклонить маятники в разные стороны на одинаковые по величине углы (рис.4).
α П
α0 |
α0 |
t
α Л
t
Рис. 4.
(Этот факт не совсем очевиден, однако можно показать, что это следует из
симметрии первоначальных отклонений маятников от положения равновесия).
Таким образом, в системе связанных маятников могут происходить как гармонические, так и негармонические колебания. Гармонические
колебания в системе с двумя или более степенями свободы называются
нормальными колебаниями системы.
Нормальные колебания представляют особый интерес, поскольку любые негармонические движения являются суперпозициями (или линейными комбинациями) этих нормальных колебаний.
Перейдем теперь к количественному описанию колебательных процессов в экспериментальной установке. Исходными являются основные уравнения вращательного движения.
Пусть каждый из маятников имеет массу m и момент инерции J . Центр инерции каждого из маятников расположен на расстоянии l от оси вращения, пружина жесткости k прикреплена к маятникам на расстоянии r от оси вращения (рис. 2). Массой пружины мы пренебрежем.
На каждый маятник действуют два момента сил: момент силы тяжести и момент сипы связи (предполагаем, что трением в оси колебаний маятников можно пренебречь). Будем считать колебания малыми, т.е. полагаем малыми углы отклонения маятников:
αЛ ,П << 1 |
(1) |
так что |
|
sinαЛ ,П ≈ αЛ ,П , cosαЛ ,П ≈ 1 |
(2) |

4
Деформация пружины равна (см. рис.2):
x = r ×sinαЛ - r ×sinαП » r ×(αЛ -αП ) |
(3) |
Используя при вычислении моментов сил приближенные равенства (2),
основные уравнения динамики вращательного движения можно записать в виде:
J |
d 2αЛ |
|
|
= -mglα |
Л |
- kr |
2 (α |
Л |
-α |
П |
) |
(4) |
||||||||
dt2 |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
J |
d 2αП |
|
|
= -mglα |
П |
+ kr |
2 (α |
Л |
-α |
П |
) |
(5) |
||||||||
dt2 |
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Введем обозначения: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
ω 0 |
= |
|
mgl |
|
, |
δ = |
|
|
kr2 |
|
|
(6) |
||||||
|
|
J |
|
|
J |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Тогда уравнения (4) и (6) |
|
|
после деления на величину J |
перепишутся в |
||||||||||||||||
следующей форме: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
d 2α |
+ω02αЛ +δ 2 (αЛ -αП ) = 0 |
(7) |
|||||||||||||||||
|
|
Л |
|
|
||||||||||||||||
|
|
dt2 |
||||||||||||||||||
|
d 2α |
+ω02αП -δ 2 (αЛ -αП ) = 0 |
(8) |
|||||||||||||||||
|
|
П |
|
|||||||||||||||||
|
|
dt2 |
||||||||||||||||||
Уберем мысленно пружину (положим |
формально жесткость k = 0 ) или |
|||||||||||||||||||
мысленно поднимем пружину совсем вверх ( r = 0 ), т.е. сделаем маятники независимыми друг от друга, не связанными. Тогда третьи члены в уравнениях (7) и (8) обратятся в нуль, и движение каждого из двух маятни-
ков опишется обычным уравнением гармонических колебаний
d 2α |
Л |
|
, |
d 2α |
, |
(9) |
|
|
+ω02αЛ = 0 |
П |
+ω02αП |
||||
dt2 |
|
dt2 |
|||||
где ω0 имеет смысл собственной частоты колебаний одного отдельно взя- того физического маятника.
Различие уравнений (7), (8) и (9) показывает, что при наличии связи между маятниками, т.е. в системе с двумя степенями свободы, движение в общем случае может не происходить по гармоническому закону.
Пусть α Л (0) и αП (0) - начальные угловые отклонения маятников. Тогда
решение уравнений (7), (8) можно записать в следующем виде (проверьте это путем подстановки приведенных решений в уравнения):
αЛ (t) = |
1 |
(αЛ (0) +αП (0))cosω1t + |
1 |
(αЛ (0) -αП (0))cosω2t |
(10) |
|
2 |
2 |
|||||
|
|
|
|
|
|
|
|
|
5 |
|
αП (t) = |
1 |
(αЛ (0) + αП (0))cosω1t − |
1 |
(α Л (0) −αП (0))cosω2t |
(11) |
|
2 |
2 |
|||||
|
|
|
|
Здесь введены обозначения:
|
|
|
ω1 = ω0 , ω2 = ω02 + 2δ 2 |
(12) |
|
Зависимости углов отклонения от времени (10), (11) указывают на тот факт, что в общем случае колебания маятников действительно не являются гармоническими, а представляют собой суперпозицию (комбинацию) двух гармонических колебаний - с частотами ω1 и ω2 . Именно эти гармонические колебания и называются нормальными колебаниями.
Теперь уместно задать вопрос: при каких условиях возбуждения в нашей экспериментальной установке возникают нормальные колебания? Точный количественный ответ, конечно, дают соотношения (10) и (11), из которых видно, что возможны две следующие ситуации (на качественном уровне мы их уже рассмотрели выше):
а) нормальные колебания первого (синфазного) типа
Пусть в начальный момент t = 0 оба маятника были отклонены в одну и ту же сторону на равные углы (см. рис.3):
αЛ (0) = α0 |
, |
αП (0) = α0 |
(13) |
Тогда (см. выражения (10) и (11)): |
|
|
|
αЛ (t) = α0 cosω1t |
, |
αП (t) = α0 cosω1t |
(14) |
Маятники совершают синфазные |
|
гармонические колебания с |
частотой |
ω1 = ω0 . Эта частота не зависит от наличии пружины (пружина "не работает").
б) нормальные колебания второго (противофазного) типа
Пусть в начальный момент t = 0 маятники были отклонены на равные углы, но в разные стороны (см. рис.4):
|
α Л (0) = −α0 |
, |
αП (0) = α0 |
(15) |
Тогда (см. выражения |
(10) и (11)): |
|
|
|
αЛ |
(t) = −α0 cosω2t |
, |
αП (t) = α0 cosω2t |
(16) |
Маятники совершают противофазные гармонические колебания с частотой ω2 . Частота ω2 больше частоты ω1 и она растет с увеличением расстояния r от оси до места закрепления пружины (см. (12)).
Таким образом, в рассматриваемой колебательной системе с двумя степенями свободы возможны два типа нормальных колебаний, и их мож- но возбудить, если отклонить маятники в начальный момент времени в соответствии с рис. 3 и 4.
6
Явление биений.
Всякое отклонение начальных условий от (13) или (15) (т.е. |αЛ (0) |¹|αП (0) |)
возбуждает оба нормальных колебания. Так что движение каждого из маятников будет представлять собой результат суперпозиции (наложения) нормальных колебаний обоих типов. (Имея в виду это иногда говорят о сложении колебаний разных частот, но одного направления колебаний).
Действительно, положим, например, в соотношениях (10), (II)
α Л (0) = 0 , |
αП (0) = α0 |
(17) |
Это значит, что в начальный момент t = 0 |
правый маятник отклонили |
|
вправо на угол α0 , а левый маятник оставили в положении равновесия. При этом выражения (10) и (11) переписываются так
αЛ |
(t) = |
1 |
|
α0 |
(cosω1t - cosω2t) |
(18) |
|||||
2 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
||
α |
П |
(t) = |
1 |
|
α |
|
(cosω t + cosω |
t) |
(19) |
||
2 |
|
|
|||||||||
|
|
|
|
0 |
1 |
2 |
|
|
|||
Преобразуем формулы (18) и (19), используя тригонометрические соотношения:
αЛ (t) = α0 sin( |
ω2 |
−ω1 |
t)×sin( |
ω2 |
+ω1 |
|
t) |
(20) |
|||||
|
2 |
|
|
|
2 |
||||||||
αП (t) =α0 cos( |
ω2 |
−ω1 |
t)×cos( |
ω2 |
+ω1 |
t) |
(21) |
||||||
|
2 |
|
2 |
||||||||||
Видно, что движение маятников не является гармоническим колебанием. В такой записи вторые сомножители описывают колебания с частотой, равной полусумме частот нормальных колебаний:
ω = (ω2 + ω1 ) / 2 |
(22) |
а первые сомножители - колебания с частотой, равной полуразности частот нормальных колебаний:
Ω = (ω2 − ω1 ) / 2 |
(23) |
В нашей установке имеется возможность сделать связь маятников слабой в том смысле, чтобы выполнялось неравенство δ << ω0 , при котором частоты
ω1 и ω2 становятся достаточно близки друг к другу. При этом

|
|
7 |
ω2 ≈ ω1 + δ /ω0 |
= ω1 + kr2 / Jω0 |
(24) |
ω ≈ ω0 , |
Ω ≈ kr2 / 2Jω0 |
(25) |
Так как
Ω << ω , |
(26) |
то первые сомножители в формулах (20) и (21) меняются сравнительно медленно. На этом основании величины
A |
(t) = |
α |
0 |
sin( |
ω2 −ω1 |
|
t) |
= |
|
α |
0 |
sin(Ω t) |
|
|
(27) |
||||||||||
|
|
||||||||||||||||||||||||
|
|
||||||||||||||||||||||||
Л |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
A |
(t) = |
|
α |
0 |
cos( |
ω2 −ω1 |
|
t) |
|
= |
|
α |
0 |
cos(Ω t) |
|
(28) |
|||||||||
|
|
|
|
|
|||||||||||||||||||||
|
|
||||||||||||||||||||||||
П |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
можно назвать периодически изменяющимися амплитудами колебаний, описываемых вторыми сомножителями в соотношениях (20) и (21).
С какой же частотой изменяются сами амплитуды AЛ (t) , AП (t) ?
Очевидно, с частотой 2Ω . В самом деле, частота Ω в выражении α0 sin(Ω t) или α0 cos(Ω t) характеризует периодичность появления "горбов" (или
"впадин") вдоль синусоиды или косинусоиды. Когда мы находим модуль α0 sin(Ω t) или α0 cos(Ω t) , то "горбы" остаются "горбами", а "впадины"
превращаются в "горбы", и в итоге "горбы" будут встречаться вдвое чаще. Это и означает, что амплитуды AЛ (t) и AП (t) периодически меняются с
удвоенной частотой, т.е. с частотой
ωБ = 2Ω = ω2 − ω1 |
(29) |
ωБ = ω2 − ω1 ≈ kr2 / Jω0 |
(30) |
В случае колебаний вида (20), (21) говорят, что происходит явление
биений: маятники |
совершают колебательное движение |
с |
частотой |
|
ω = (ω2 + ω1 ) / 2 ) |
с периодически нарастающими |
и |
убывающими |
|
амплитудами колебаний. Переменные величины |
AЛ (t) |
и AП (t) |
||
называются амплитудами биений, а величина ωБ = (ω2 |
− ω1 ) |
называется |
||
частотой биений. |
|
|
|
|
Явление биений возникает всегда, когда одновременно возбуждают оба типа нормальных колебаний: движение представляет собой не-

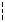 α
α