ГОС / MODUL_11_El_mat

М12 - 1.Основные ф-лы тригон-ии. Тригон-ие Ур-ия и нер-ва и методы их реш-я.

Опр. Если (.)М числовой окруж-ти соотв-т числу t, то абсцисса (.)М наз-т косинусом числа t и обозн-т cos t, а ординату (.)М - синусом числа t и обозначают sin t.

Опр. Отношение синуса числа t к косинусу того же числа наз-т тангенсом числа t и обозн-т tg t. Отношение косинуса числа t к синусу того же числа наз-т котангенсом числа t и обозначают ctg t.

Основные тригон-ие тождества:

1.sin²+cos²=1.

2. cos²=1 -sin²

3. sin²=1- cos²

4.

5.

6.

7.

8.

Формулы сложения.

Т1.

Док-во

Пусть и-произв.числа. Положим для опред-ти

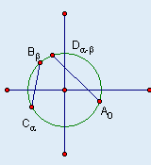
Отметим на числ.окр-ти (.)А,В,С кот. cоотв.числам 0, ,.Постр.(.)D.кот.соотв.числу

.Дуга AD=дуге ВС. Хорда AD=хорде ВС.Найд.коорд.этих (.)

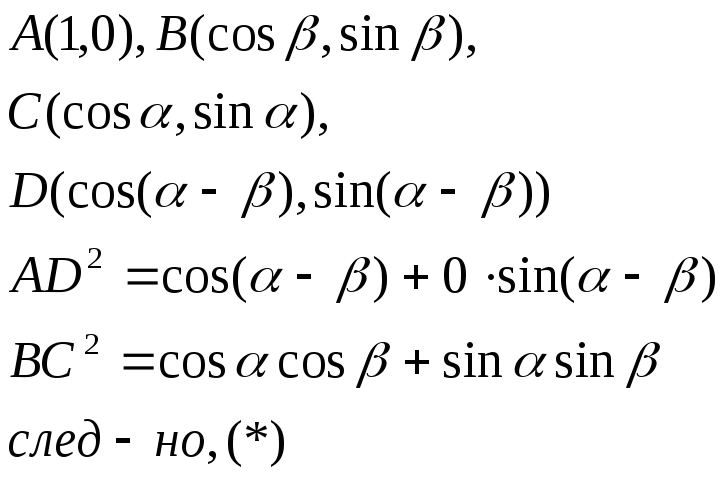
Следствие:

1.

2.

3.

Т2.

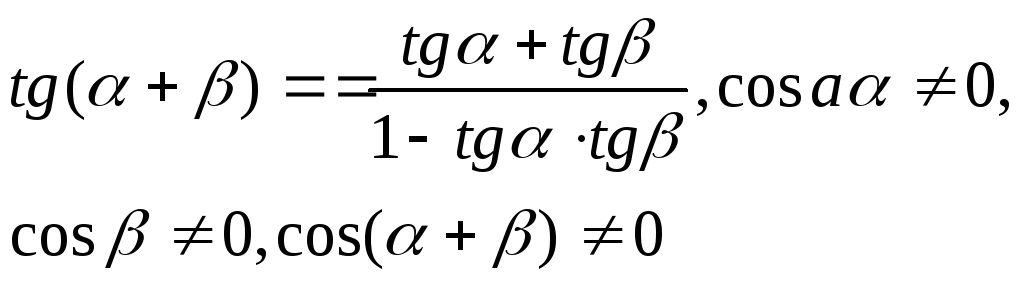
Док-во

Следствие:

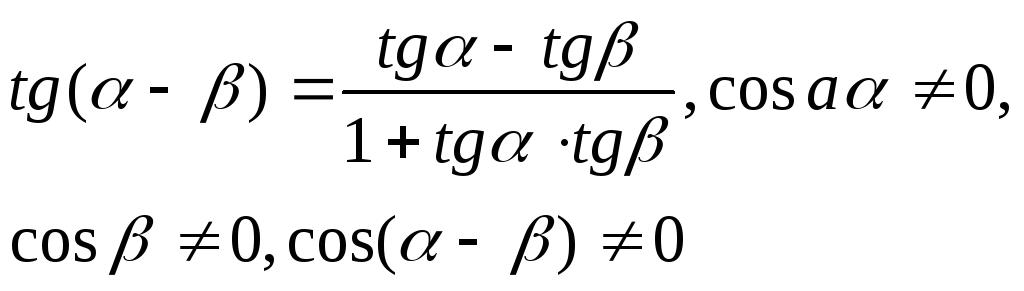
А также:

Ф-лы 2-го и полов-го аргумента

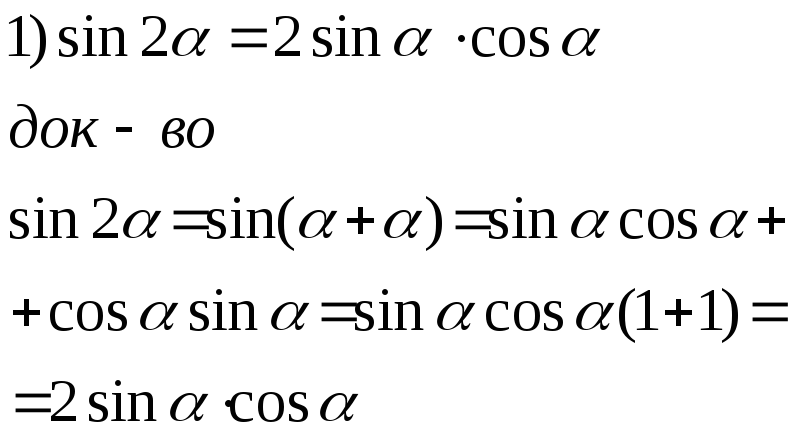
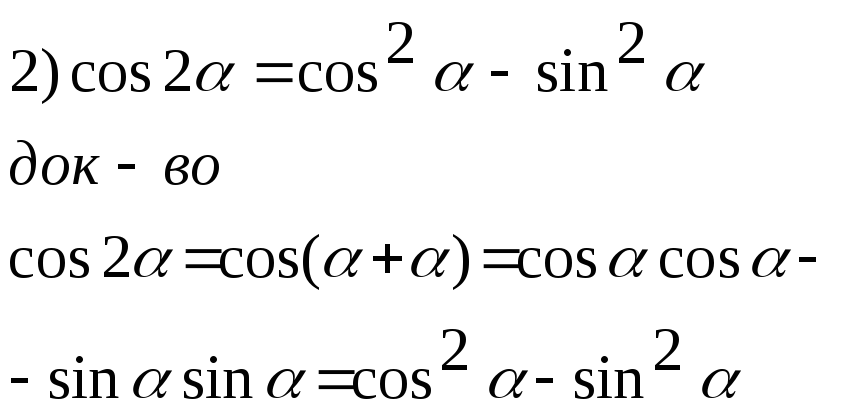
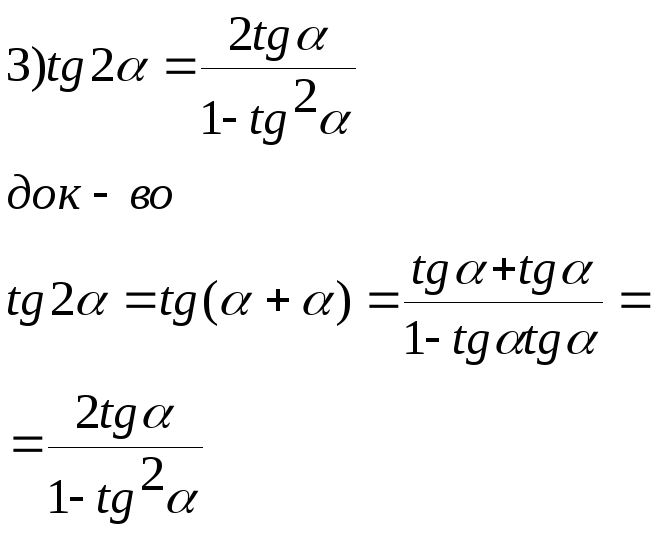
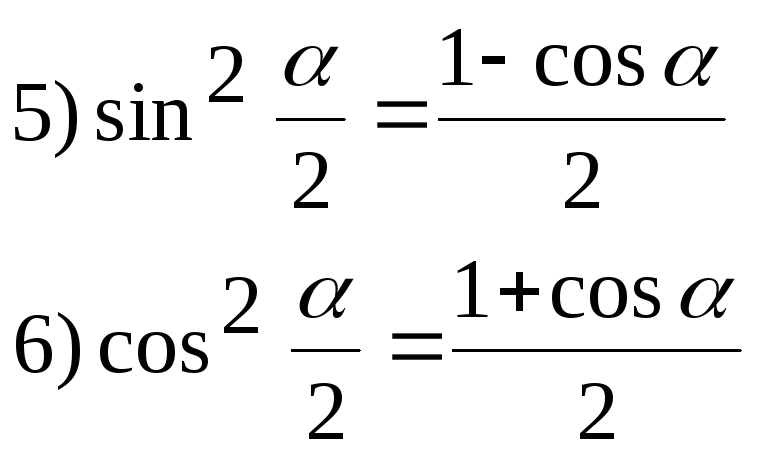
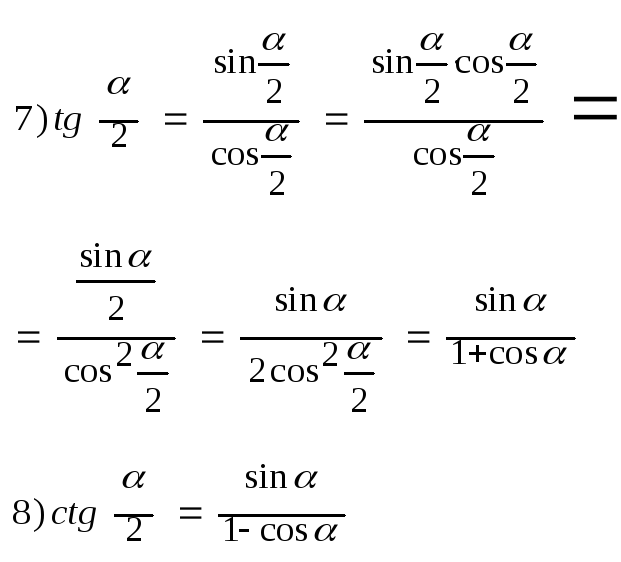
Формулы понижения степени

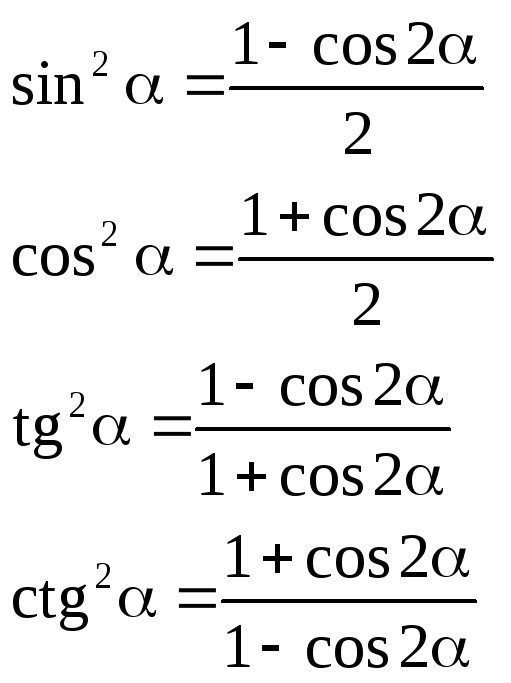
Преобразование суммы и разности одноим-х тригон-их ф-й в произв-е:

Преобраз-е произведение тригоном-х ф-й в суммы и разности одноим-х ф-й:

Док-во

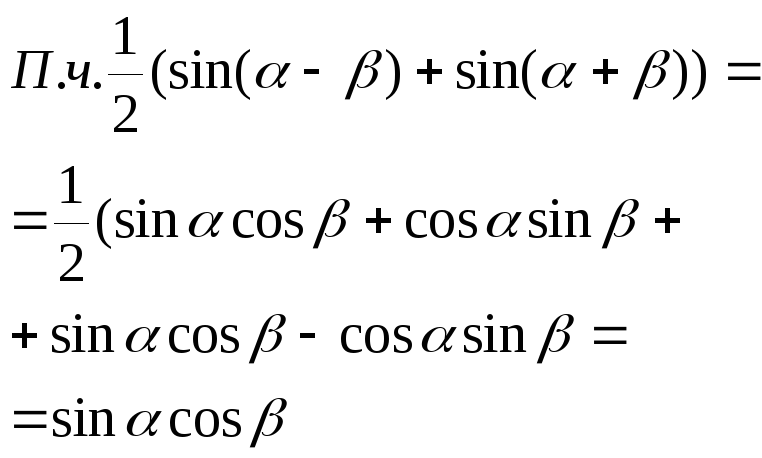
Аналогично:

Универсальная подстановка:

1)

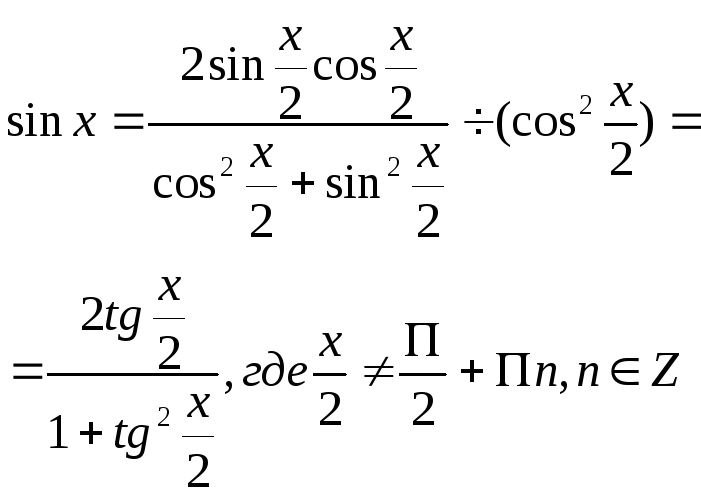
2)

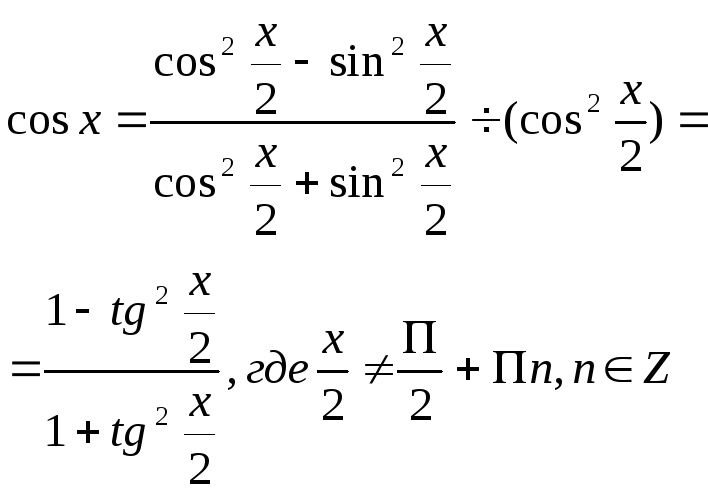
3)

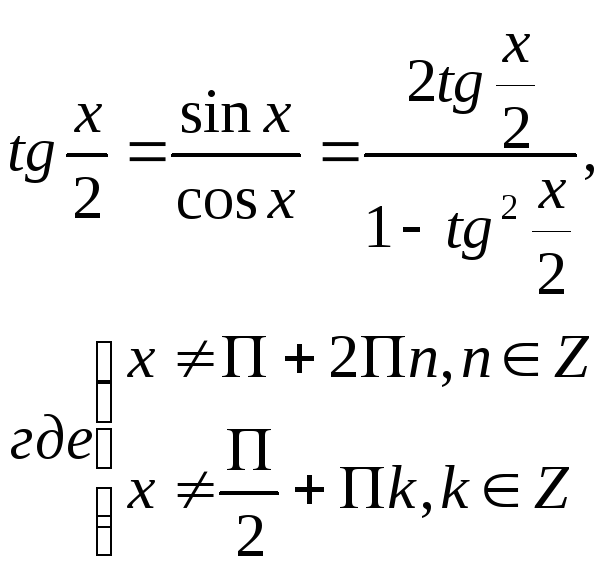
Опр. Триг. наз ур-е, содержащее переменные только под знаком тригонометрической ф-и.

Триг ур отличаются тем, что если область их опр-я условием задачи не ограничена, то они либо имеют бескон-е множество решений, либо решений нет.

Триг ур явл трансцендентными ур-ми, а это значит, что не сущ-т общих методов их реш-я поэтому в школьной практике рассм-ся только те триг ур, алгоритм реш-я к-рых можно явно указать. Процесс реш-я любого триг ур состоит в след-м: реш-ся триг ур относ-но входящих в него триг ф-ций. В рез-те реш-м каждую из них (дизъюнкцию). Объед-е реш-й простейших дает реш-е исходного ур-я.

Осн.виды триг.ур-ий:

1. Простейшие и к ним сводящиеся.

Реш-е простейших ур-й:

1.sin x=a, x=(-1)ⁿarcsin a+2n, nZ. Ур-е имеет реш-е при а1. Реш-е с помощью единичной окр-ти. Реш-й бесконечно много, но на окр-ти обозначены 2-мя точками(из соображений симметрии).

2.cosx=a, x=

3.tg x=a.

4.ctg a=a

2.Ур-я вида:

Решаются заменой переменных

3.Однородные ур-я

a) Однородные ур-я1ст asin(x)+bcos(x)=0, где

Реш-ся делением обеих частей на cos(x) или sin(x)

b) Однородные ур-я2ст

Реш-ся делением обеих частей на cos²(x) или sin²(x).При этом потери корней не будет,т.к.числа вида и корнями не будут.

4.ур-е вида a sin (x)+b cos(x)=c. где

1 сп: сведение к однор

2сп.введ-е вспом. угла

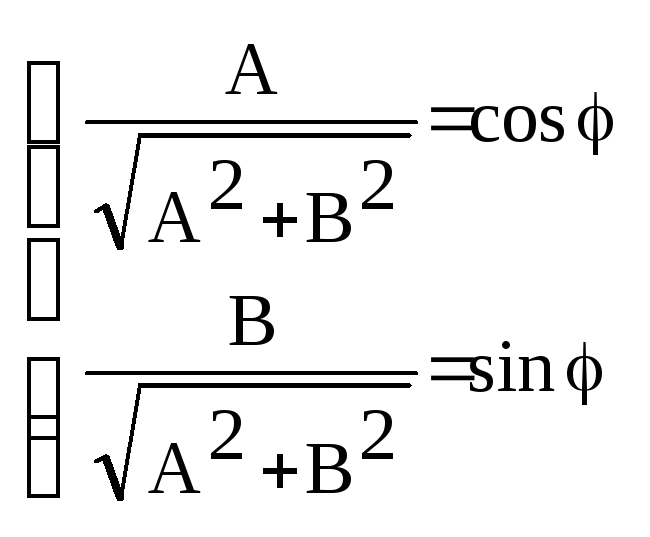
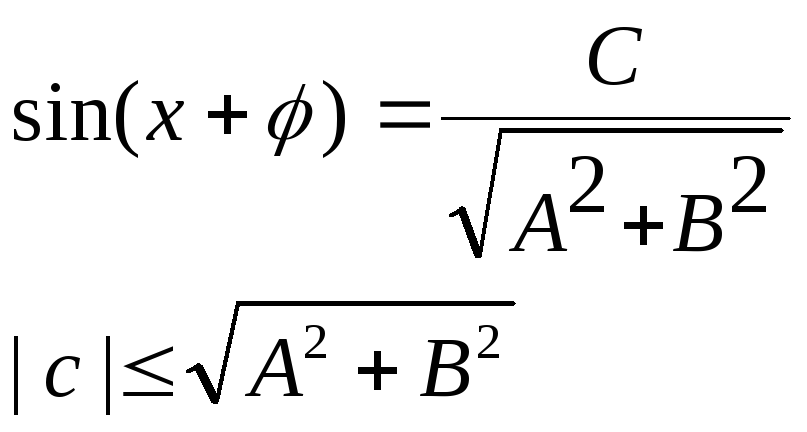
4. Решение с помощью универ.триг.подстановки

5.Ур-я вида

Реш-ся подстановкой

М12 - 2Алгебр-е и тринсц-ые ур-ия, нер-ва и их сис-мы. Равнос-ость. Аналит-й и граф-й методы решения.

Опр1. Ур-е –равенство f(x)=g(x) или f(x)=0, где f и g –ф-ии.Решить ур-е-значит значит найти множество всех его корней или доказать, что их нет

Опр2. Корень ур-я- значение неизвестных, при которых ур-е обращается в тождество

Опр3. Пусть (1) какое-то ур-ие, а ур-ие(2) получено в рез-те нек-ых преобразований. Если сущ-ет такое х₀ , кот-ое явл-ся корнем ур-ия (2), но не яв-ся корнем ур-ия (1), то говорят, что появился посторонний корень.

Опр.4. Два (1) и (2) наз-ся равнос-ыми, если все реш-ия ур-ия (1) явл-ся реш-ми ур-я (2), и наоборот, или когда оба ур-ия не имеют реш-ий.

Опр.5. Если ур-ие (2) содержит все реш-ия ур-ия (1), то ур-ие (2) яв-ся следтвием ур-ия (1), т.е. все реш-ия ур-ия (1) входят в реш-ия ур-ия (2).

Опр.6. Область опр-ия ур-ия есть мн-во область опр-ия f(x), а – обл опр-ия g(x).

Т.1. Если к обеим частям ур-ия (1) прибавить выр-ие , имеющее смысл на мн-ве Х – обл. опр-ия ур-ия, то получим новое ур-ие, равнос-ое данному: (2).

Док-во. Пусть - реш-е ур-ия (1), тогда -верное числовое рав-во, некот-ое число. Если к верному числовому рав-ву прибавить одно и тоже число, то получим верное числовое рав-во: корень ур-ия (2).

Обратно. Пусть - реш-е ур-ия (2), тогда -верное числовое рав-во, -некот-ое число. Если от ур-ия (2) отнять , то получим верное числовое рав-во: прибавить одно и тоже число, то получим верное числовое рав-во: корень ур-ия (1).

Значит мн-во реш-ий (1) и (2) совпадают

Теорема доказана

Т.2. Если обе части ур-ия (1) умножить на одно и тоже выр-е, имеющее смысл на области опр-ия ур-ия Х, и при всех выр-ие , то получим новое ур-ие , равнос-е дан-му.

Т.3.

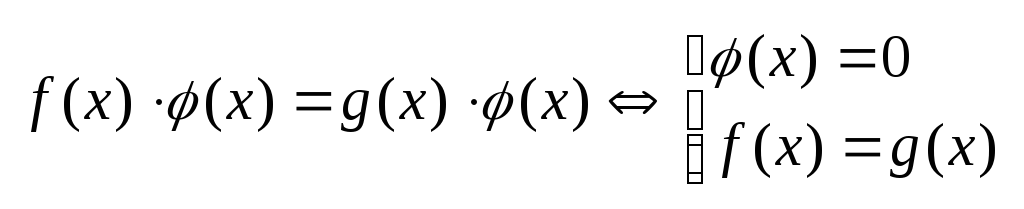
Т.4.

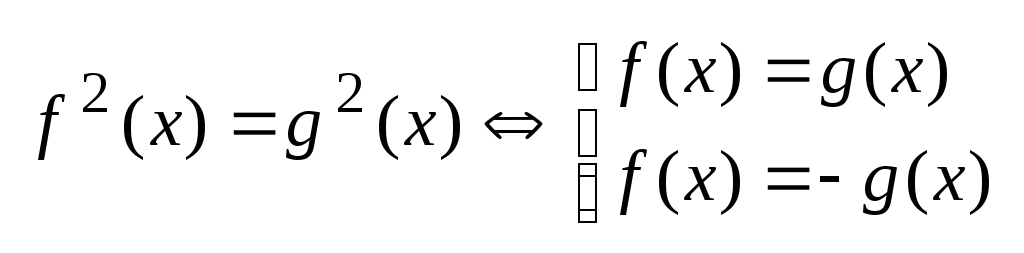
Т.5.

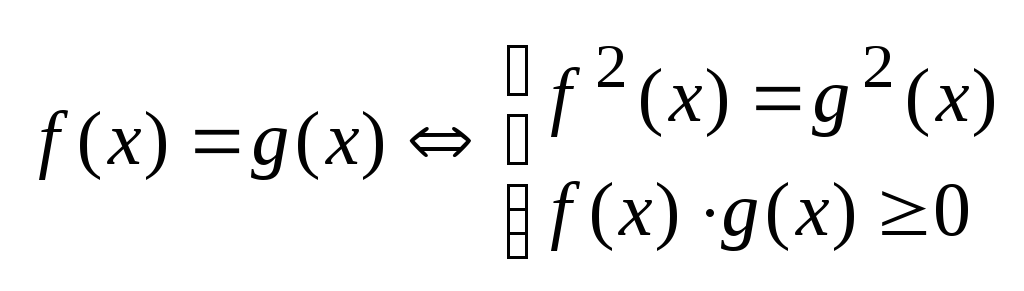
Замена ур-ия равнос-ым ему наз-ся равнос-ым переходом. Проверка не нужна, ОДЗ не находим, но следим при переходе от одного ур-ия к другому за обл. опр-ия ур-ия.

Опр.7. Нер-ва с одной переменной – неопр-ые высказ-я, где поставлена задача найти все значения переменной, кот-ые обращают данное нер-во в верное числовое нер-во.

Область опр-ия нер-ва: , где -обл. опр-ия f(x), -обл. опр-ия g(x).

Опр.8. Два нер-ва наз-ся равнос-ми, если совпадают их мн-ва реш-ий.

Т.6.

Т.7. Если к обеим частям нер-ва (1) прибавить выр-ие , имеющее смысл на мн-ве Х – обл. опр-ия нер-ва (1), то получим нер-во равнос-ое данному: (2).

Т.8. Если обе части нер-ва (1) домножить на одно и тоже выр-ие, имеющее смысл на области опр-ия нер-ва и приним-ее положит-ые (отрицат-ые) знач-я для всех х, то получим нер-во (), равнос-ое данному.

Т.9. (Для всех f(x)>0, g(x)>0)

Т.10.

Т.11.

Т.12.

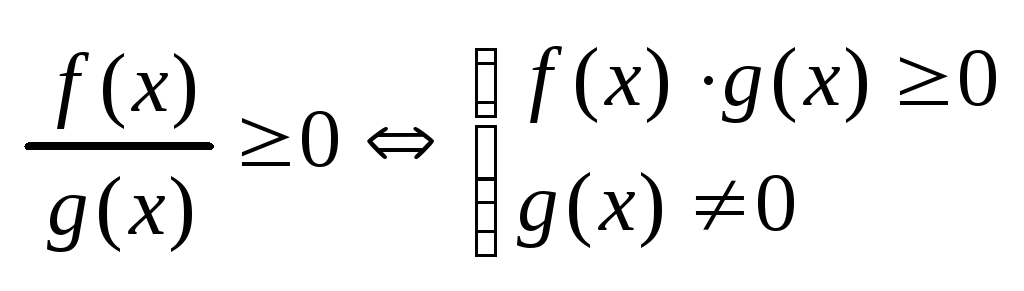
Ур-ия и нер-ва, сод-щие модуль

1., а-число

а)

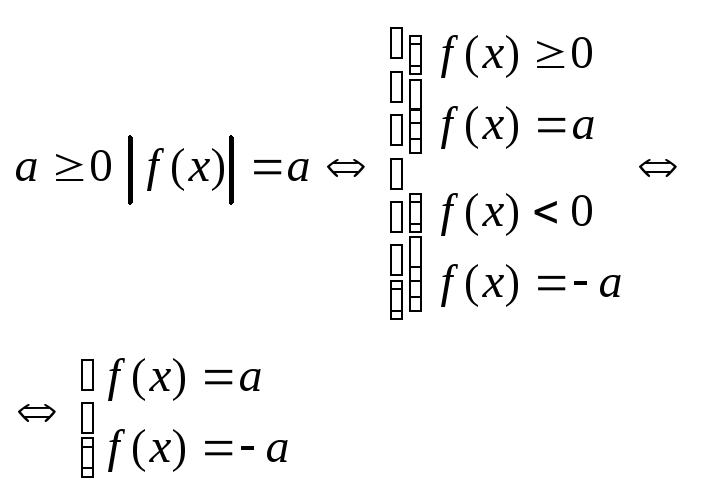
б) а<0 – реш-ий нет

2.

а)

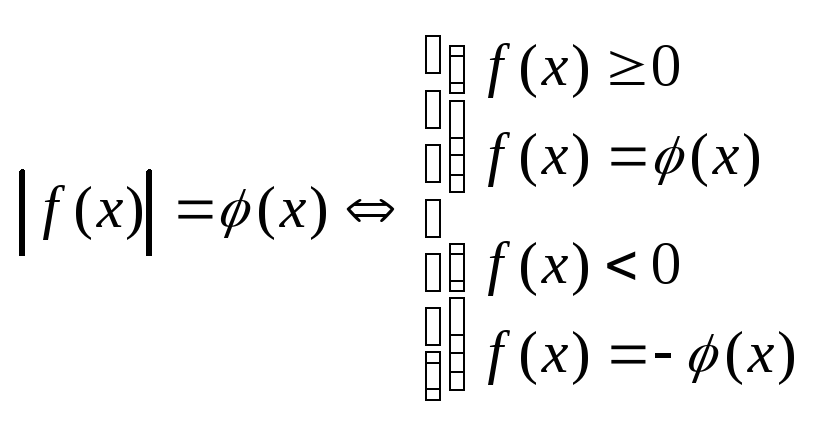
б)

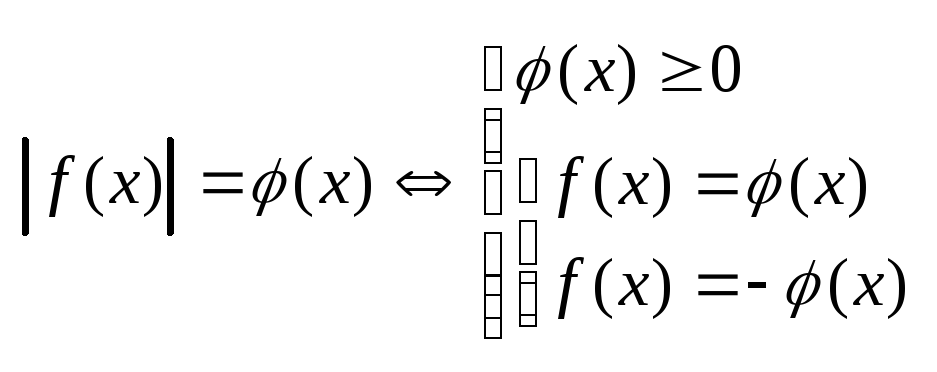
в)

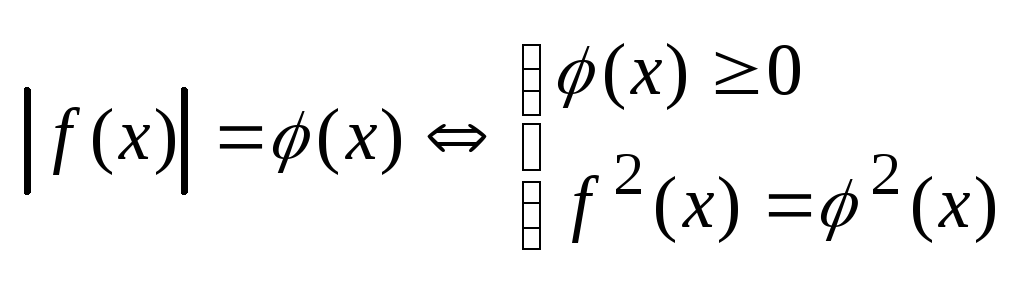
3.

а)

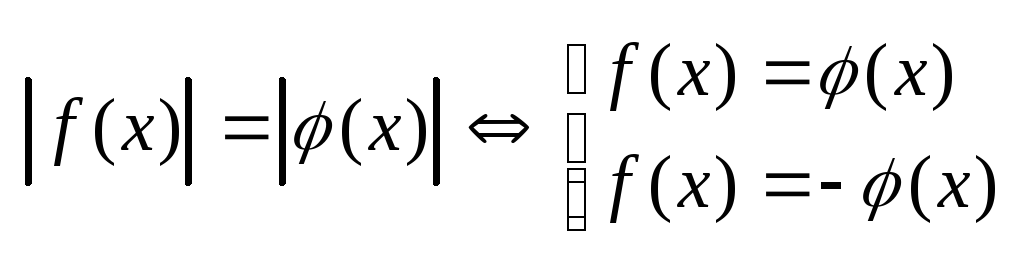
б)

Ур-ия, содерж-е два и более модулей реш-ся методом интервалов.

Виды нер-в и способы их реш-ия.

1.

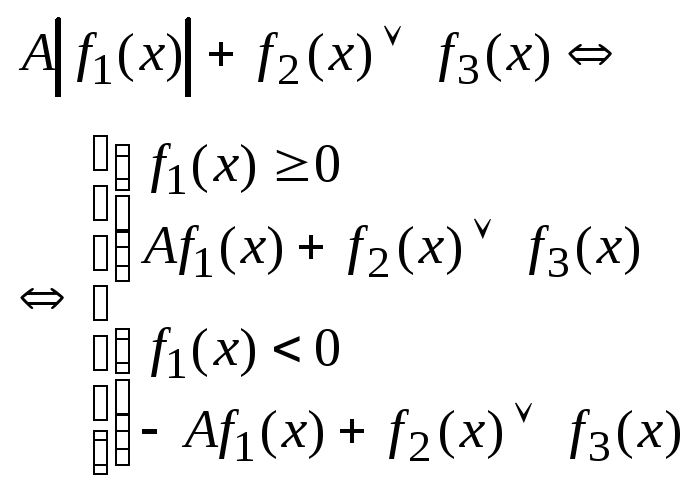
-общий знак сравнения

2.

решается методом интервалов

3. , а-число

а) а>0

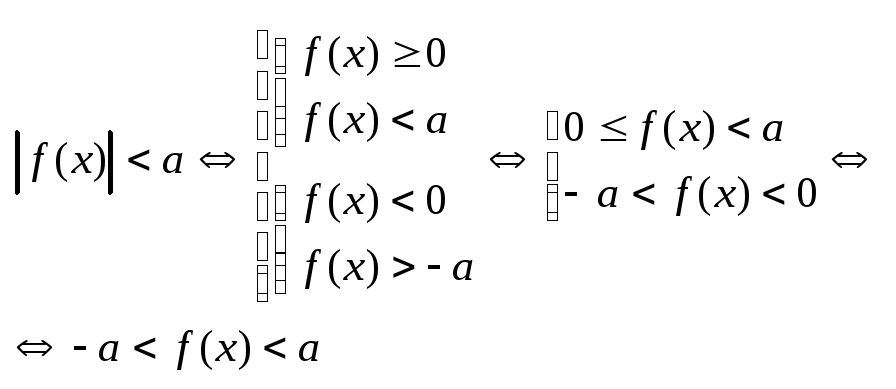
б) а<0 – реш-ий нет

4. , а-число

а)

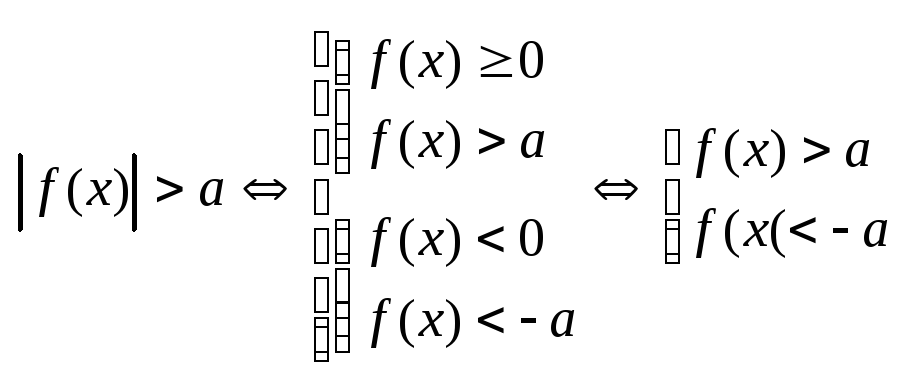
б) а<0, то

5.

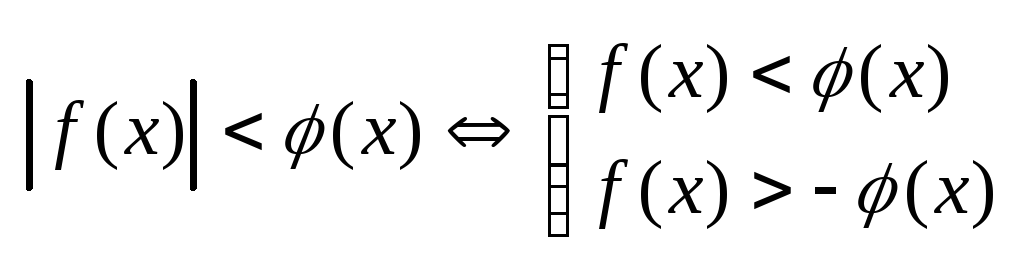
6.

7.

Метод интервалов основан на том, что непрерывная ф-ция меняет знак только при переходе через нули ф-ции нечетной кратности.

Ур-ия высших степеней.

Опр.9. Ур-ие вида наз-ся симметрическим.

Рац-ые и дробно-рац-ые ур-ия.

Опр.10. Выр-ие, состоящее из букв и чисел, соед-ых между собой знаками арифм-их действий наз-ся рац-ым относительно входящих в него букв.

Опр.11. Целым рац-ым ур-ем степени n наз-ся ур-е вида: Если а0=1, то ур-ие наз-ся приведенным.

Опр.12. Рац-ое выр-ие наз-ся целым, относит-о некот-ой, если в нем нет операции деления на выраж-е, содерж-ее эту букву.

Опр.13. Ур-ие , где f(x), g(x) – цел-е рац-ые выраж-ия, наз-ся целым рац-ым ур-ем.

Основные методы реш-ия.

Разлож-е на множ-ли: ур-е нужно привести к виду .

Подстановка: введение новой переменной y=g(x). Выраж-е f(x) представляют черех у, находят корни нового ур-ия и делают обратную подстановку.

Графич-ий способ и др.

Нер-ва рац-ые и дробно-рац-ые ршаются аналогичными способами.

Иррац-ые ур-ия и нер-ва.

Опр.14. Ур-е, в кот-ом переем-ая стоит под знаком корня наз-ся иррац-ым.

Иррац-ые ур-ия реш-ся путем уединения корня и возведения обеих частей в степень, равную показателю корня. При этом исп-ся теорема о равнос-ости ур-ий и нужно следить за обл-ю опред-ия.

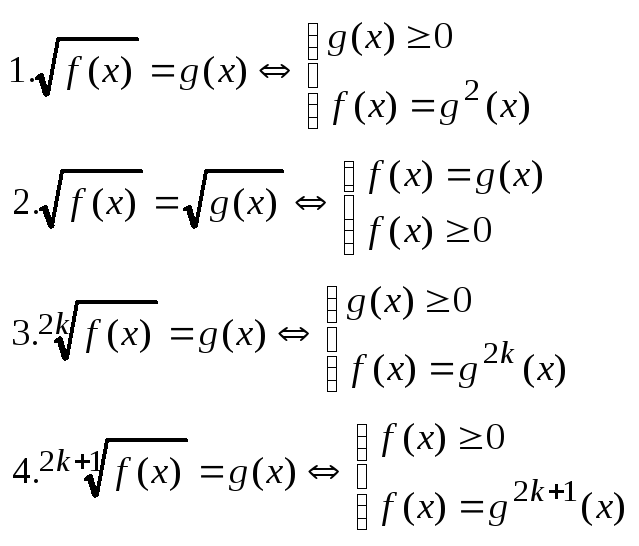
Опр.15. Нер-во наз-ся иррац-ым, если переем-ая стоит под знаком корня

Любое иррац-ое нер-во можно свести к виду:

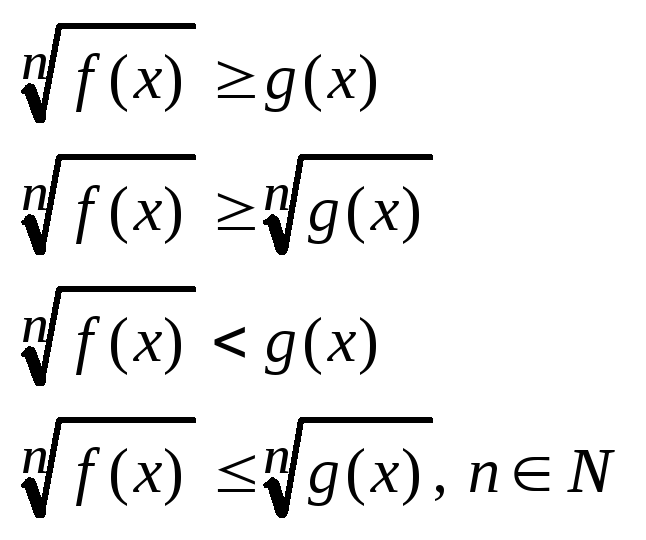
1. Если n – нечетное, то пользуемся теорами о равнос-ости.

2. n – четное

Пусть n=2

1)

2)

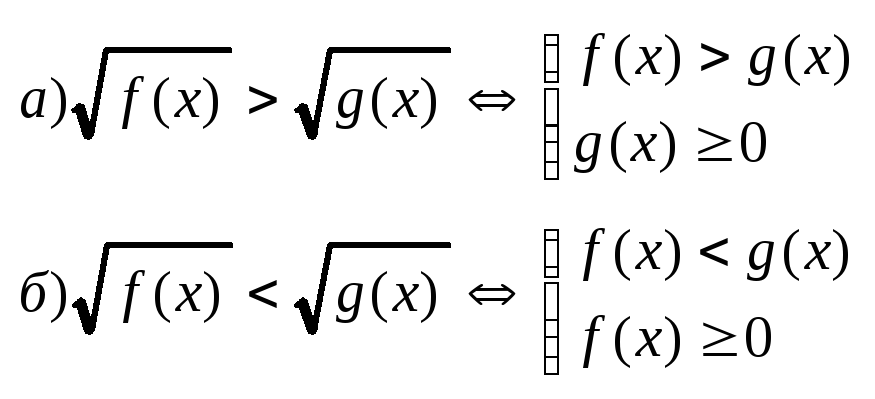
Показ-ые ур-ия и нер-ва.

Опр.16. Ур-ия, сод-щие показат-ые, логариф-ие, тригоном-ие ф-ции наз-ся трансцендентными.

Опр.17. Ур-ие, сод-щее переем-ую только в показателе степени наз-ся показ-ым.

1.

Если 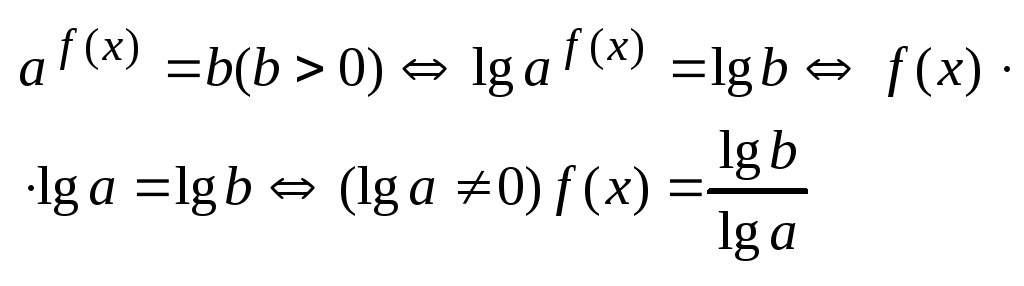2. решается путем вынесения общего множителя

3. реш-ся путем замены на

4. - однородный многочлен, реш-ся путем деления на .

Показ-ые нер-ва реш-ся на основе монотонности показат-ых ф-ций, используются те же приемы, что и при реш-ии ур-ий.

Показательно-степенные ур-ия и нер-ва.

Опр.18. Ур-ия, содержащие ф-цию, у кот-ой переменная нах-ся и в основании степени и в показателе, наз-ся показ-но-степен-ми:

Пок-но-степ-ая ф-ция опред-на, когда:

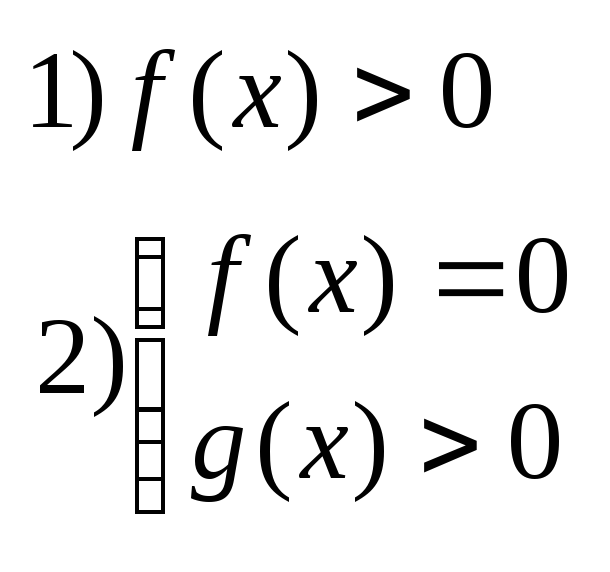
1.

2.

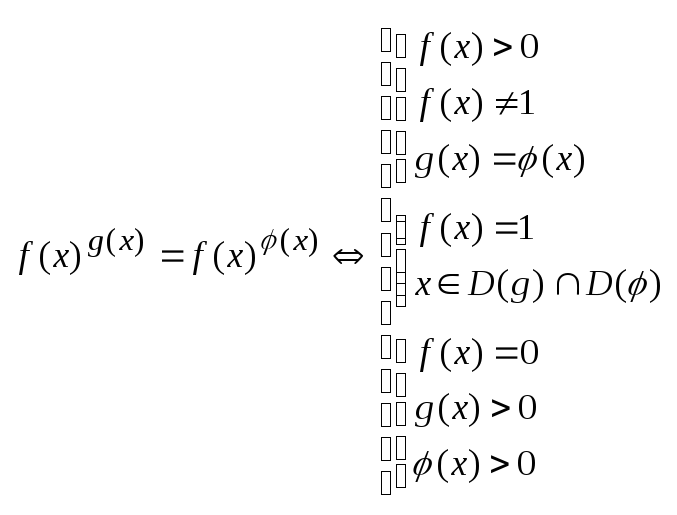
Нер-ва, сод-щие пок-степ-ую ф-цию.

1.

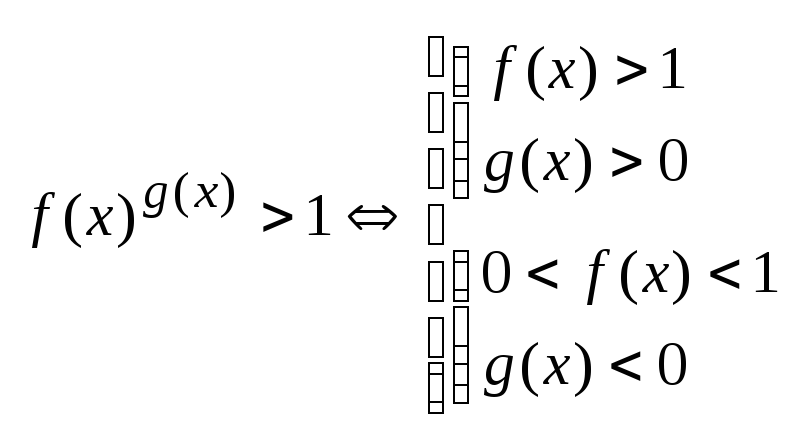
2.

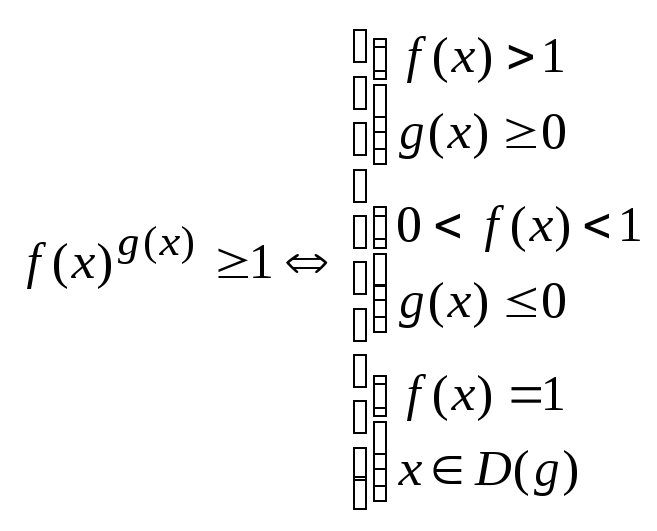
3.

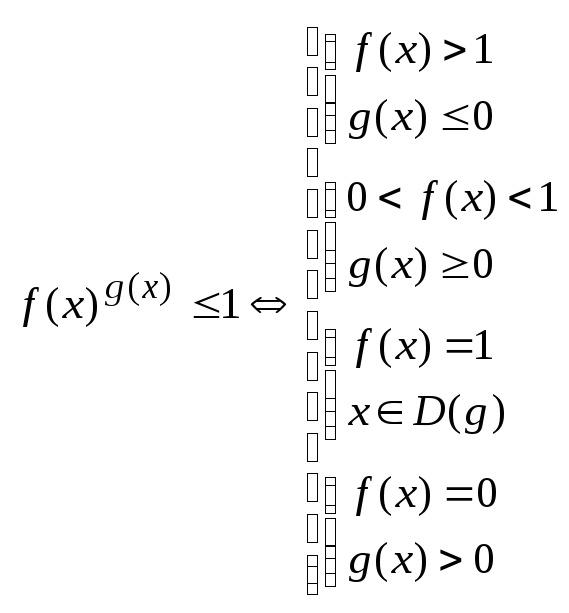
4.

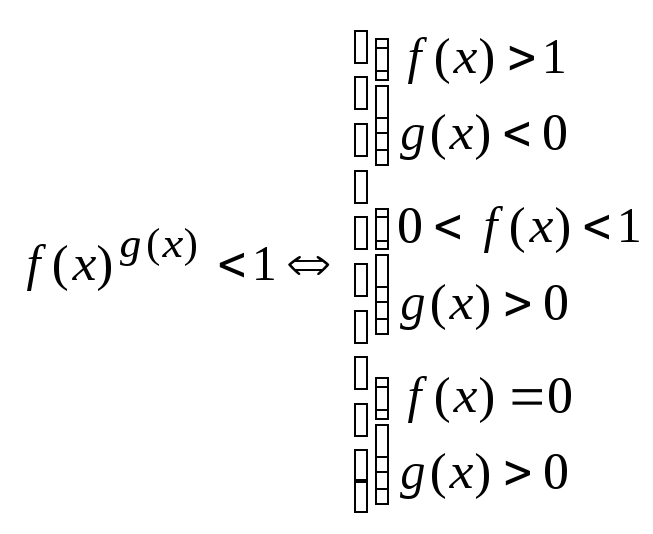
Логариф-ие ур-ия и нер-ва.

Опр.19. Ур-ие, в кот-ом переем-ая нах-ся под знаком логарифма, наз-ся логар-им.

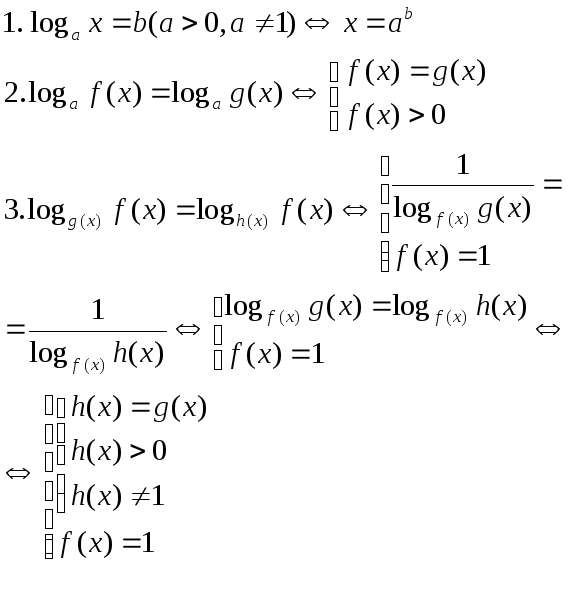
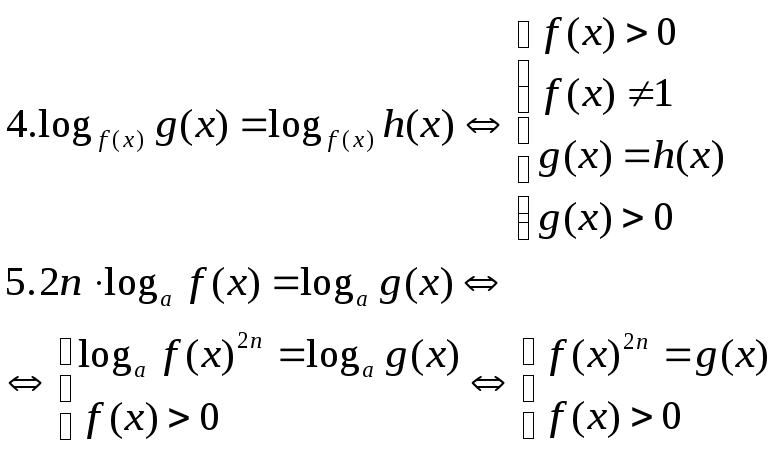
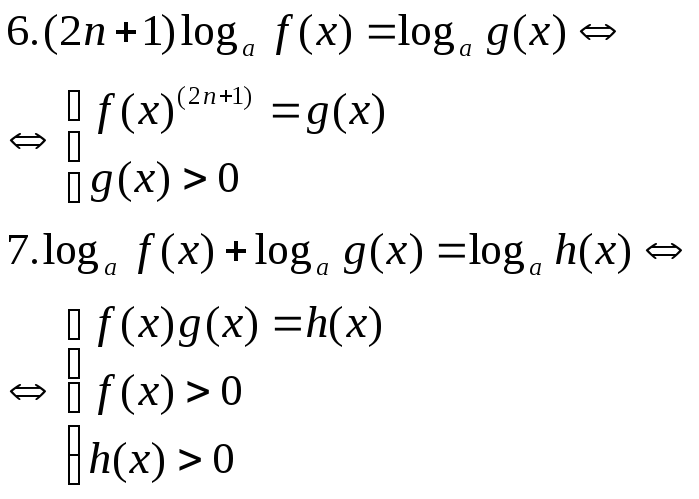Лог-ие нер-ва.

Как правило, трансцендентые ур-ия и нер-ва требуют нестандартных методов рш-ия, таких как: использование ОДЗ; исп-ие монотонности, множ-ва значений ф-ций; исп-ие производной ф-ции; графический метод.

Графический метод.

При реш-ии ур-ий и нер-в этим методом исп-ют эскизы графиков ф-ций. При этом эскиз помогает найти решение, но писать ответ из графика нельзя. Ответ нужно обосновать.