5. Интервальное оценивание параметров распределения

Интервальной называют оценку, которая определяется двумя числами - концами интервала, покрывающего оцениваемый параметр. Доверительным называют интервал, который с заданной надежностью  покрывает заданный параметр.

1. Интервальной оценкой генерального среднего х_г (математического ожидания а = М(Х)) нормально распределенного количественного признака Х по выборочной средней при известном среднем квадратическом отклонении (Х) генеральной совокупности служит доверительный интервал:

, (13)

где - точность оценки,n - объем выборки, t - значение аргумента функции Лапласа Ф(t), при котором Ф(t) = /2. При неизвестном среднем квадратическом отклонении  (и объеме выборки n < 30) интервальной оценкой (с надежностью ) математического ожидания а = М(Х) служит доверительный интервал:

, (14)

где s - исправленное выборочное среднее квадратическое отклонение, величина t_ - квантиль распределения Стьюдента, соответствующий заданным значениям n и .

2. Интервальной оценкой (с надежностью ) среднего квадратического отклонения  нормально распределенного количественного признака Х по исправленному выборочному среднему квадратическому отклонению s служит доверительный интервал

, при q < 1, (15)

, при q > 1,

где q находят по распределению “хи” по заданным значениям n и 

3. Интервальной оценкой (с надежностью  неизвестной вероятности p биномиального распределения по относительной частоте  служит доверительный интервал p₁ < p < p₂ , где

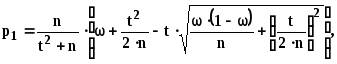(16)

где n - общее число испытаний; m - число появления события;  -относительная частота, равная отношению m / n; t — значение аргумента функции Лапласа, при котором Ф(t) = /2 ( — заданная надежность).

При больших значениях n (порядка сотен) можно принять в качестве границ доверительного интервала:

(17)

4. Для равномерного и показательного законов распределения доверительный интервал для математического ожидания будем строить так же, как и для нормального. Доверительный интервал для параметра  показательного распределения определяется по формуле:

, (18)

где х_л , х_п - границы доверительного интервала для математического ожидания.

6. Порядок выполнения лабораторной работы

Файл с лабораторной работой “Выборочный метод ...” представляет из себя рабочую книгу табличного процессора Excel и содержит 2 листа Исходный и Расчет. На листе Исходный расположены 2 управляющие кнопки “Ввод варианта” и “Моделирование”. Лист Исходный защищен от несанкционированного ввода информации, то есть открытыми для ввода значений остаются только несколько ячеек, о назначении которых будет сказано ниже.

Для ввода выборки значений случайной величины необходимо ввести номер варианта в отведенную для этой цели ячейку. Номер варианта n_вар обязан удовлетворять условию: 1  n_вар  200. После этого при нажатии кнопки “Ввод варианта” с помощью специально написанной программы на VBA генерируется выборка значений случайной величины, причем объем выборки n также определяется случайным образом с помощью датчика случайных чисел в диапазоне: 100  n  200. Выборка выводится в виде вектор-столбца, в котором для удобства работы пронумерованы его компоненты. Одновременно лист Расчет очищается от имеющейся на нем предыдущей информации.

Для обработки выборки ее необходимо перенести на лист Расчет. Для вычисления точечных оценок параметров распределения и построения гистограммы вводится два дополнительных столбца, в первом определяются квадраты вариант выборки, а во втором выборка записывается в возрастающем порядке, то есть в виде вариационного ряда. Ниже столбцов, содержащих выборку, производится вычисление точечных оценок параметров распределения. Вид листа Расчет, содержащий эти данные имеет следующий вид:

Таблица 1.

	A	B	C	D
1	№	Xi	X^2	X1
2	1	5.405	29.209	4.578
3	2	10.062	101.251	4.585
4	3	8.194	67.145	4.596
5	4	6.495	42.179	4.608
6	5	8.824	77.864	4.632
7	6	7.978	63.659	4.675
8	7	8.447	71.363	4.758
9	8	9.144	83.607	4.820
165	164	10.701	114.508	11.439
166	165	5.528	30.566	11.457
167	166	10.680	114.053	11.461
168	M =	8.086	69.553
169	D =	4.170
170	s =	2.048

В столбцы А и В перенесена выборка из листа Исходный объемом n = 166. В столбце С расположены квадраты вариант выборки. Для этого в ячейку С2 введена формула “=B2*B2” и распространена на область С2-С167. В область D2-D167 скопирована выборка из области В2-В167 и отсортирована в порядке возрастания с помощью кнопки панели инструментов. Если этой кнопки нет на панели инструментов, то она может быть размещена на ней с помощью команды Сервис-Настройка-Панели инструментов-Категория-Таблица. В раскрывшемся окне расположен перечень кнопок, необходимая кнопка с помощью мыши перетаскивается на любую панель инструментов. В этом же перечне кнопок находится кнопка “Автосуммирование”, которая может быть использована при вычислении выборочных характеристик.

В ячейке В168 вычисляется выборочное среднее по формуле (1): “=СУММ(В2:В167)/166”. Функция СУММ(В2:В167) может быть введена по кнопке “Автосуммирование”. В ячейке С168 вычисляется средний квадрат выборки по формуле “=СУММ(С2:С167)/166”. В ячейке В169 вычисляется выборочная дисперсия по формуле (2): “=С168-В168*В168”. В ячейке В170 вычисляется исправленное выборочное среднее квадратическое отклонение по формуле (3): “=КОРЕНЬ(166/165*В169).

При построении диаграммы в лабораторной работе принимаем число частичных интервалов равным N = 10. Для построения гистограммы рассчитаем на листе Расчет таблицу следующего вида.

Таблица 2.

	E	F	G	H	I	J	K
1			№	Xi	Y j	m j	n j
2	Х min =	4.577	1	4.577	4.921	0	19
3	X max =	11.461	2	5.266	5.610	19	17
4	h =	0.688	3	5.954	6.298	36	13
5	n =	166	4	6.642	6.986	49	11
6	M(x) =	8.085	5	7.331	7.675	60	15
7	D(x) =	4.170	6	8.019	8.363	75	21
8	s(x) =	2.048	7	8.707	9.052	96	17
9			8	9.396	9.740	113	18
10			9	10.084	10.428	131	21
11			10	10.772	11.117	152	14
12			11	11.461		166

В ячейку F2 внесена минимальная варианта, то есть скопировано первое значение вариационного ряда из ячейки D2, в ячейку F3 внесена максимальная варианта, то есть скопировано последнее значение вариационного ряда из ячейки D167, в ячейке F4 вычислена длина частичных интервалов h по формуле (6): “=(F3-F2)/10”, в ячейку F5 введен объем выборки n, в ячейки F6-F8 скопированы вычисленные ранее выборочные характеристики из ячеек В168-В170. В столбец G2-G12 введены порядковые номера опорных точек, которые разбивают весь диапазон реализованных значений выборки на частичные интервалы. Очевидно, что число этих точек равно N + 1 = 11. В столбец Н2-Н12 введены значения этих точек x_j по формуле (5). Для этого в ячейку Н2 введена формула: “=$F$2+$F$4*(G2-1)” и распространена на область Н2-Н12. Знак “$” указывает на абсолютную ссылку, которая не меняется при использовании автозаполнения области. В столбец I2-I11 введены значения средних точек y_j частичных интервалов по формуле (4). Для этого в ячейку I2 введена формула: “(H3+H2)/2” и распространена на область I2-I12. Средних точек y_j для рассматриваемой гистограммы должно быть N = 10. В столбец J2-J12 вводятся номера вариант m_j вариационного ряда, удовлетворяющие условию x_i < x_j . В столбец К2-К11 введены частоты n_j частичных интервалов, вычисляемые по формуле: n_j = m_j+1 - m_j . Для этого в ячейку К2 введена формула: “=(J3-J2)” и распространена на область К2-К11.

Гистограмма строится по данным столбца К2-К11 с использованием “Мастера диаграмм”. Для этого надо выделить область К2-К11, нажать на пиктограмму “Мастера диаграмм” на панели инструментов и выбрать в раскрывшемся меню Тип - Гистограмма - Обычная гистограмма. Для данных, представленных в таблице 2 гистограмма имеет, представленный на рис. 1. По форме гистограммы можно сделать предположение, что исследуемая случайная величина имеет равномерный закон распределения.

Выдвинутую гипотезу необходимо проверить с помощью критерия согласия Пирсона. Проверка гипотезы осуществляется в таблице, в которую включаются данные таблицы 2. Часть листа Расчет, в котором проводятся соответствующие вычисления представлена в таблице 3.

Рис. 1.

Таблица 3.

	E	F	G	H	I	J	K	L	M
1			№	Xi	Y j	m j	n j	nt	(n-nt)^2/nt
2	Х min =	4.577	1	4.577	4.921	0	19	16.6	0.346
3	X max =	11.461	2	5.266	5.610	19	17	16.6	0.009
4	h =	0.688	3	5.954	6.298	36	13	16.6	0.780
5	n =	166	4	6.642	6.986	49	11	16.6	1.889
6	M(x) =	8.085	5	7.331	7.675	60	15	16.6	0.154
7	D(x) =	4.170	6	8.019	8.363	75	21	16.6	1.166
8	s(x) =	2.048	7	8.707	9.052	96	17	16.6	0.009
9			8	9.396	9.7403	113	18	16.6	0.118
10			9	10.084	10.428	131	21	16.6	1.166
11			10	10.772	11.117	152	14	16.6	0.407
12			11	11.461		166		хи набл	6.048
13								хи крит	14.067

Столбцы Е-К таблицы 3 полностью совпадают с соответствующими столбцами таблицы 2. В области L2-L11 вычислены теоретические вероятности равномерного распределения по формуле (7). Для этого в ячейку L2 внесена формула: “=$F$4*$F$5/($F$3-$F$2)” и распространена на область L2-L11. В области М2-М11 вычисляются относительные квадраты отклонений теоретических и эмпирических частот для дальнейшего вычисления наблюдаемого значения критерия .Для этого в ячейкуМ2 вносится формула: “=(K2-L2)^2/L2” и распространяется на область М2-М11. Наблюдаемое значение критерия вычисляется в ячейкеM12 по формуле (12): “=СУММ(M2:M11)”. В ячейке M13 вычисляется критическое значение критерия по уровню значимости = 0,05 и числу степеней свободы для равномерного закона распределения k = N - m_p - 1 = 7 с помощью встроенной функции:

“=ХИ2ОБР(0.05; 7)“.

Данные таблицы 3 показывают, что . Таким образом, выдвинутая гипотеза о равномерном законе распределения исследуемой случайной величины не отвергается.

Для математического ожидания генеральной совокупности необходимо найти доверительный интервал с надежностью = 0,95 по формуле (14). Квантиль распределения Стьюдента t_вычисляется с помощью встроенной функции:

СТЬЮДРАСПОБР(1-; n).

Часть листа Расчет, в которой реализовано вычисление доверительного интервала для генерального среднего, представлена в таблице 4.

Таблица 4.

	F	G	H	I	J
14	Доверительный интервал для мат. ожидания
15	нижняя граница
16	7.772
17	верхняя граница
18	8.399

В ячейку F16 внесена формула:

“=$F$6-СТЬЮДРАСПОБР(0.05;$F$5)*$F$8/КОРЕНЬ($F$5)”,

а в ячейку F18 - формула:

“=$F$6+СТЬЮДРАСПОБР(0.05;$F$5)*$F$8/КОРЕНЬ($F$5)”.

Правильность проведенных расчетов проверяется сравнением функции распределения, рассчитанной на основе выбранного закона распределения по определенным выборочным характеристикам, с эмпирической функцией распределения, рассчитанной на основе действительного закона распределения в результате обработки выборки большого объема. Эта обработка производится автоматически в процессе генерации выборки с помощью программы, написанной на VBA. Перед запуском процедуры обработки необходимо заполнить таблицу “Эмпирическая функция распределения” на листе Исходный. В эту таблицу необходимо внести аргументы эмпирической функции распределения х, которые являются решением уравнения F^*(x) = p, где р - заданное значение. Для равномерного закона функция распределения имеет вид:

,

где [a; b] - отрезок распределения равномерной случайной величины.

Так как в результате обработки выборки принимается, что x_min  a, x_max  b, то:

.

По результатам обработки выборки получено, что x_min = 4,578 и x_max = 11,461 , поэтому в ячейку Е12 листа Исходный вводится формула: “=4.578+E11*(11.461-4.578)” и распространяется на область Е12-М12. В ячейку F12 вводится объем выборки для моделирования, равный n = 1000. После этого нажимается управляющая кнопка “Моделирование” листа Исходный и в таблице “Результаты моделирования” выводятся значения эмпирической функции распределения по данным генерируемой выборки. Вид листа Исходный после отработки программы представлен в таблице 5.

Таблица 5.

Эмпирическая функция распределения
F(x)	0.1		0.2		0.3			0.4	0.5			0.6	0.7	0.8	0.9
x	5.266		5.954		6.642			7.331	8.019			8.707	9.396	10.084	10.772
Объем выборки			1000
Результаты моделирования
F(x)	0.093	0.194		0.296				0.398	0.507			0.614	0.705	0.813	0.899
Номер текущей варианты							1000

Сравнение двух эмпирических функций распределение позволяет говорить об их удовлетворительном совпадении.

Выше был приведен порядок расчета лабораторной работы для случая, когда обрабатывалась выборка из равномерной генеральной совокупности. Рассмотрим изменения для случая, когда исследуемый признак распределен по нормальному закону.

Расчет выборочных характеристик (таблица 1) и построение гистограммы (таблица 2) в этом случае производятся так же, как и для равномерного закона распределения. Пусть гистограмма имеет следующий вид (рис. 2).

Рис. 2.

По форме гистограммы можно сделать предположение, что исследуемая случайная величина имеет нормальный закон распределения. Выдвинутая гипотеза проверяется с помощью критерия Пирсона. Результаты расчетов представлены в таблице 6.

Таблица 6.

	E	F	G	H	I	J	K	L	M
1			№	Xi	Y j	m j	n j	nt	(n-nt)^2/nt
2	Х min =	-2.142	1	-2.142	-1.368	0	4	2.683	0.647
3	X max =	13.329	2	-0.595	0.179	4	6	8.187	0.584
4	h =	1.547	3	0.952	1.726	10	25	18.467	2.312
5	n =	174	4	2.499	3.273	35	26	30.791	0.746
6	M(x) =	5.117	5	4.047	4.820	61	38	37.950	0.000
7	D(x) =	7.875	6	5.594	6.367	99	34	34.573	0.010
8	s(x) =	2.814	7	7.141	7.914	133	25	23.282	0.127
9			8	8.688	9.461	158	10	11.589	0.218
10			9	10.235	11.008	168	3	4.264	0.375
11			10	11.782	12.556	171	3	1.160	2.920
12			11	13.329		174		хи набл	7.937
13								хи крит	14.067

В данной таблице по сравнению с таблицей 3 изменено только заполнение столбца L2-L11 при вычислении теоретических частот нормального распределения по формулам (8)-(9). Для этого в ячейку L2 вносится формула:

“=$F$5*$F$4/$F$8*НОРМРАСП((I2-$F$6)/$F$8;0;1;0)”,

которая распространяется на область L2-L11. Первый параметр функции НОРМРАСП является аргументом плотности нормированного распределения (9), второй и третий параметры равны параметрам нормированного распределения N(0; 1), четвертый параметр, равный 0, указывает на то, что вычисляется плотность распределения.

Данные таблицы 6 показывают, что . Таким образом, выдвинутая гипотеза о нормальном законе распределения исследуемой случайной величины не отвергается.

Доверительный интервал для математического ожидания генеральной совокупности определяется так же, как и в случае равномерной случайной величины (таблица 4).

При заполнении таблицы “Эмпирическая функция распределения” квантили нормального распределения целесообразно заполнять с использованием встроенной функции НОРМОБР(p; ; s), где p = F(x) - заданное значение функции распределения. По результатам обработки выборки получено, что = 5,117 и s = 2,814. В ячейку Е12 листа Исходный вносится формула: “=НОРМОБР(Е11; 5.117; 2.814)” и распространяется на область Е12-М12. Остальные действия и интерпретация полученных результатов остаются без изменения по сравнению со случаем равномерного закона (таблица 5).

Рассмотрим изменения в порядке расчета при исследовании признака генеральной совокупности с показательным законом распределения. Расчет выборочных характеристик (таблица 1) и построение гистограммы (таблица 2) в этом случае производятся так же, как и для равномерного закона распределения. Пусть гистограмма имеет следующий вид (рис. 3).

Рис. 3.

По форме гистограммы можно сделать предположение, что исследуемая случайная величина имеет показательный закон распределения. Выдвинутая гипотеза проверяется с помощью критерия Пирсона. Результаты расчетов представлены в таблице 7.

Таблица 7.

	E	F	G	H	I	J	K	L	M
1			№	Xi	Y j	m j	n j	nt	(n-nt)^2/nt
2	Х min =	0.038	1	0.038	2.710	0	82	80.925	0.014
3	X max =	53.491	2	5.383	8.056	82	43	41.044	0.093
4	h =	5.345	3	10.728	13.401	125	20	20.817	0.032
5	n =	165	4	16.074	18.746	145	9	10.558	0.230
6	M(x) =	7.874	5	21.419	24.092	154	7	5.355	0.505
7	D(x) =	66.082	6	26.764	29.437	161	1	2.716	1.084
8	s(x) =	8.154	7	32.110	34.782	162	1	1.377	0.103
9	l =	0.127	8	37.455	40.128	163	1	0.698	0.129
10			9	42.800	45.473	164	0	0.354	0.354
11			10	48.145	50.819	164	1	0.179	3.743
12			11	53.491		165		хи набл	6.290
13								хи крит	15.507

В данной таблице по сравнению с таблицей 3 в ячейку F9 внесено значение выборочного параметра показательного закона по формуле (11): “=1/F6” и изменено заполнение столбца L2-L11 при вычислении теоретических частот нормального распределения по формулам (10). Для этого в ячейку L2 вносится формула:

“165*(EXP(-$F$9*H2)-EXP(-$F$9*H3))”

которая распространяется на область L2-L11.

В ячейке L12 вычисляется критическое значение критерия по уровню значимости = 0,05 и числу степеней свободы для показательного закона распределения k = N - m_p - 1 = 8 с помощью встроенной функции:

СТЬЮДРАСПОБР(0.05; 8).

Данные таблицы 7 показывают, что . Таким образом, выдвинутая гипотеза о нормальном законе распределения исследуемой случайной величины не отвергается.

Доверительный интервал для математического ожидания генеральной совокупности определяется так же, как и в случае равномерной случайной величины (таблица 4). Доверительный интервал для параметра показательного распределения определяется по формуле (18). Часть листа Расчет, в которой реализовано вычисление доверительного интервала для генерального среднего и параметра показательного распределения представлена в таблице 4.

Таблица 8.

	F	G	H	I	J
14	Доверительный интервал для мат. ожидания
15	нижняя граница
16	7.772
17	верхняя граница
18	8.399
19	Доверительный интервал для лямбда
20	Нижняя граница
21	0.110
22	Верхняя граница
23	0.151

Строки 14-18 заполнены так же, как и в таблице 4. В ячейку F21 внесена формула: “=1/F18”, а в ячейку F23 внесена формула: “=1/F16”.

При заполнении таблицы “Эмпирическая функция распределения” квантили х показательного распределения находятся из решения уравнения:

.

Решая это уравнение относительно х, получим:

.

Так как по результатам обработки выборки выборочное значение параметра показательного закона распределения равно _в = 0,127 , то в ячейку Е12 листа Исходный необходимо ввести формулу:

“=-LN(1-E11)/0.127”

и распространить ее на область Е12-М12. Остальные действия и интерпретация полученных результатов остаются без изменения по сравнению со случаем равномерного закона (таблица 5).