Вязкость. Движение жидкости в трубах

Все реальные жидкости и газы имеют внутреннее трение, которое также называется вязкостью. Вязкость является причиной постепенного прекращения движения жидкостей и газов после прекращения действия причин, его вызывающих.

Измерения показывают, что при медленном течении скорость жидкости изменяется от нуля в непосредственной близости к стенкам трубы до максимальной на оси трубы. Жидкость при этом оказывается как бы разделённой на тонкие цилиндрические слои, которые скользят друг относительно друга не перемешиваясь. Такое течение называетсяламинарным или слоистым (лат. lamina – пластинка, полоска).

И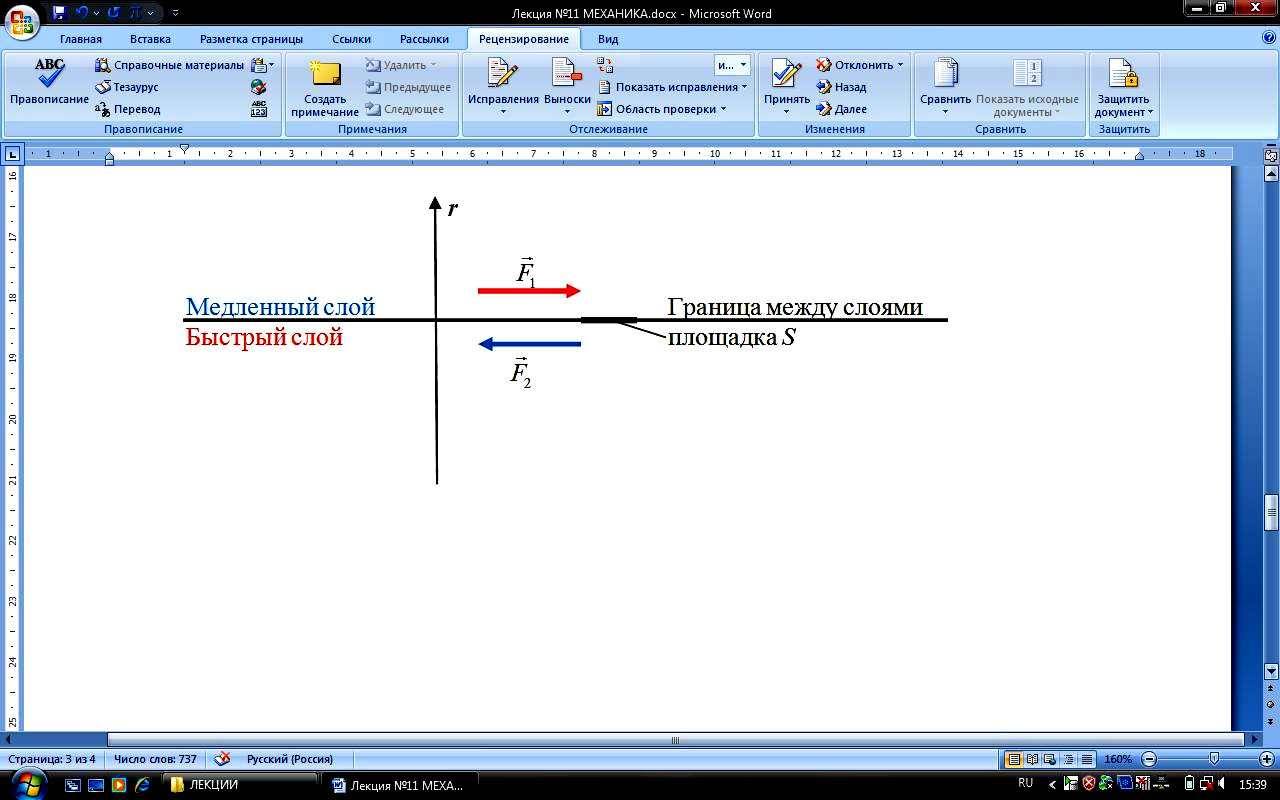з опыта известно, что для поддержки постоянного течения жидкости в трубе, необходимо наличие на концах трубы разности давлений. При стационарном течении жидкости без ускорения необходимость сил, обусловленных разным давлением на концах трубы, указывает на то, что эти силы уравновешиваются силами, тормозящими движение. Это силы внутреннего трения и на границах между слоями жидкости, между жидкостью и стенками.

Для модуля силы внутреннего трения экспериментально установлено:

_{– закон Ньютона,}

здесь: η – динамическая вязкость, – производная, показывающая как быстро меняется в данном месте скорость в направлении, перпендикулярном к площадке S.

Н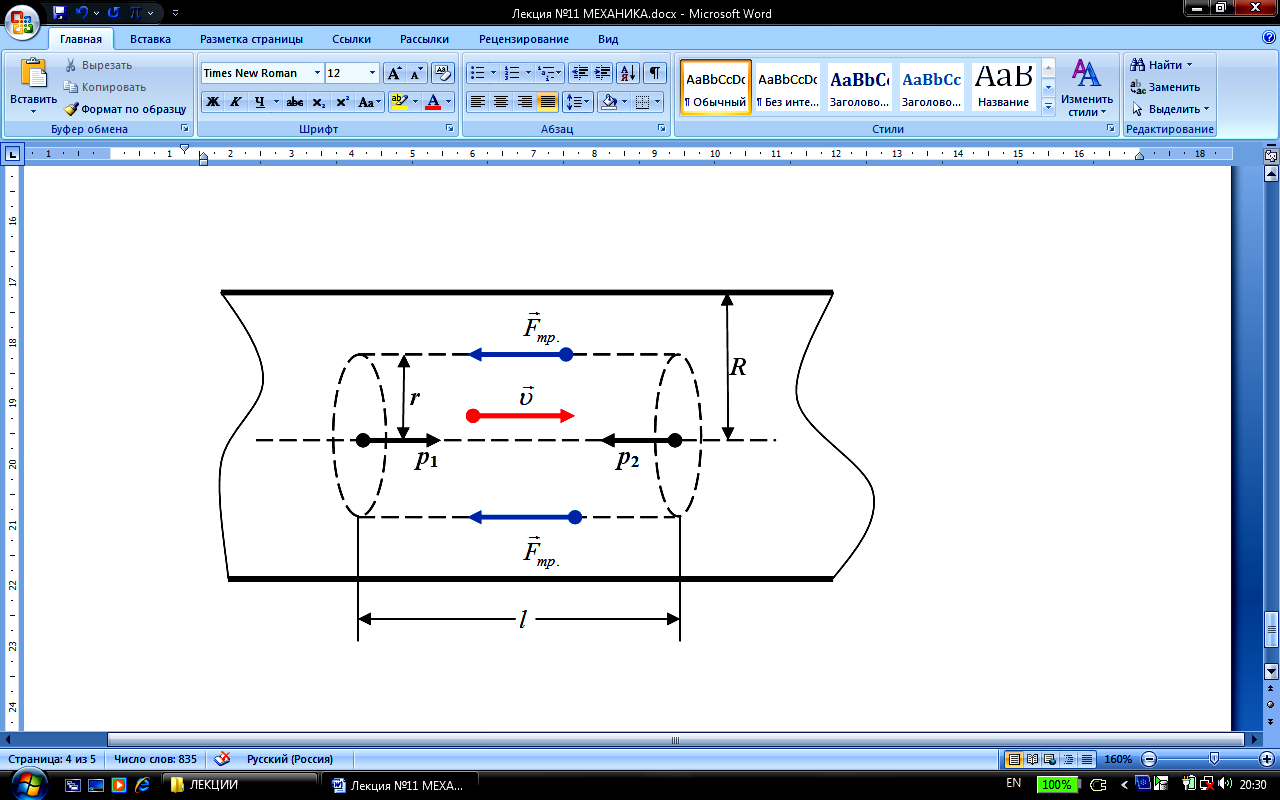айдём закон изменения модуля скорости слоёв жидкости при ламинарном течении и в трубе. Выделим воображаемый цилиндрический объём жидкости радиусаr и длины l. При стационарном течении ускорение этого объёма равно нулю. Следовательно: сумма сил, действующих на цилиндр равна нулю.

На цилиндр действуют в горизонтальном направлении:

- на основания цилиндра равнодействующая сил давления ;

- на боковую поверхность сила вязкого трения , гдеη – динамическая вязкость, , т.к. скорость слоёв жидкости уменьшается в направлении возрастания r.

При стационарном течении F_давл.=F_тр.. Следовательно . Отсюда:. В результате интегрирования:.

Постоянная С определяется из граничного условия υ_|r=R=0:

.

После подстановки: .

Скорость на оси трубы: . Тогда:

.

При ламинарном течении модуль скорости изменяется с расстоянием от оси трубы по параболическому закону.

Вычислим поток жидкостиQ (объём жидкости), протекающий через поперечное сечение трубы в единицу времени. Выделим слой радиусом r и толщиной dr. Через него поток жидкости .Поток жидкости Q определяется интегрированием:

,

где S – площадь сечения трубы. После подстановки в эту формулу :

– формула Пуазейля.

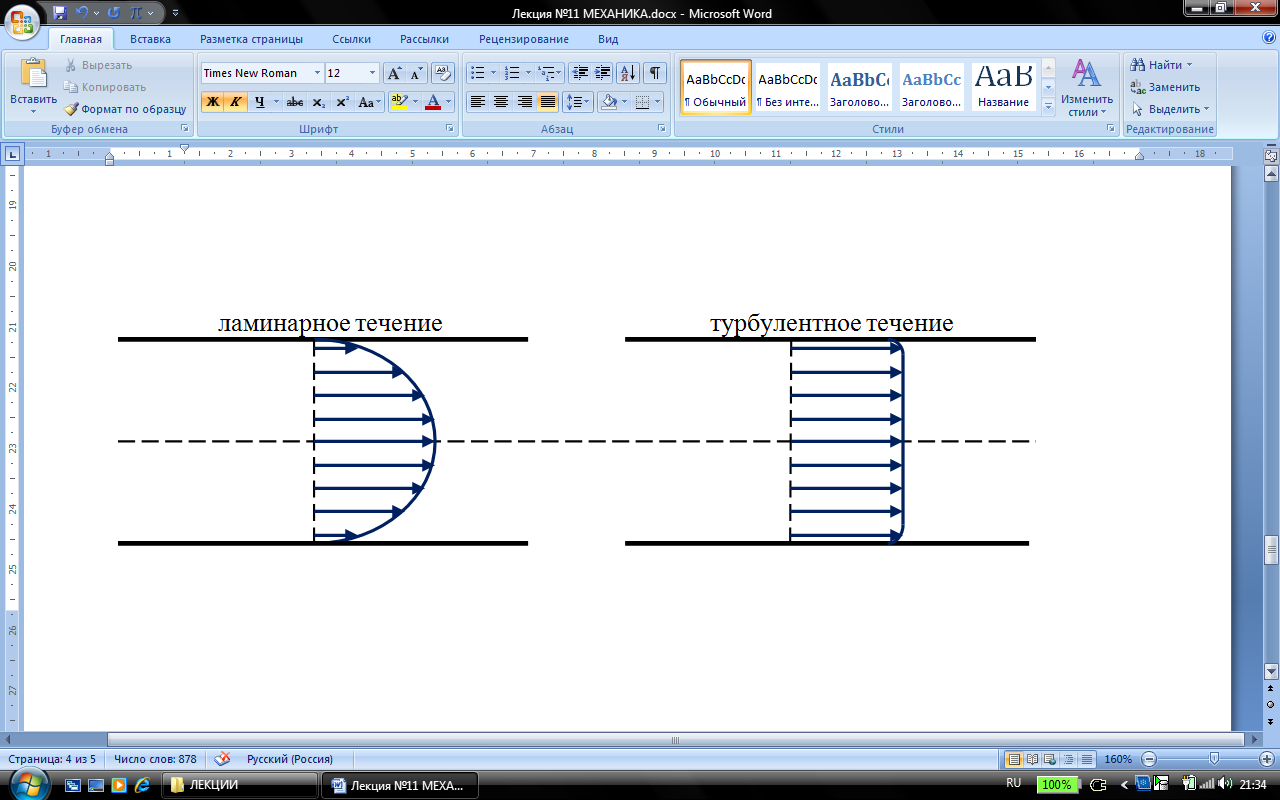
В случае нестационарного течения скорость частиц в каждой точке пространства всё время беспорядочно изменяется. Такое течение называется турбулентным. При турбулентном течении происходит интенсивное перемешивание жидкости.

Осборн Рейнольдс (английский физик 1842-1912 гг.) установил, что характер течения определяется значением безразмерной величины

–число Рейнольдса,

где ρ – плотность жидкости или газа, υ – средняя по сечению трубы скорость потока, η – вязкость жидкости или газа, l – характерный для поперечного сечения потока размер.

При малых значениях Re течение носит ламинарный характер. Начиная с критического значения Re, течение становится турбулентным. Для трубы .

Величину называют кинематической вязкостью. С учётом этого .

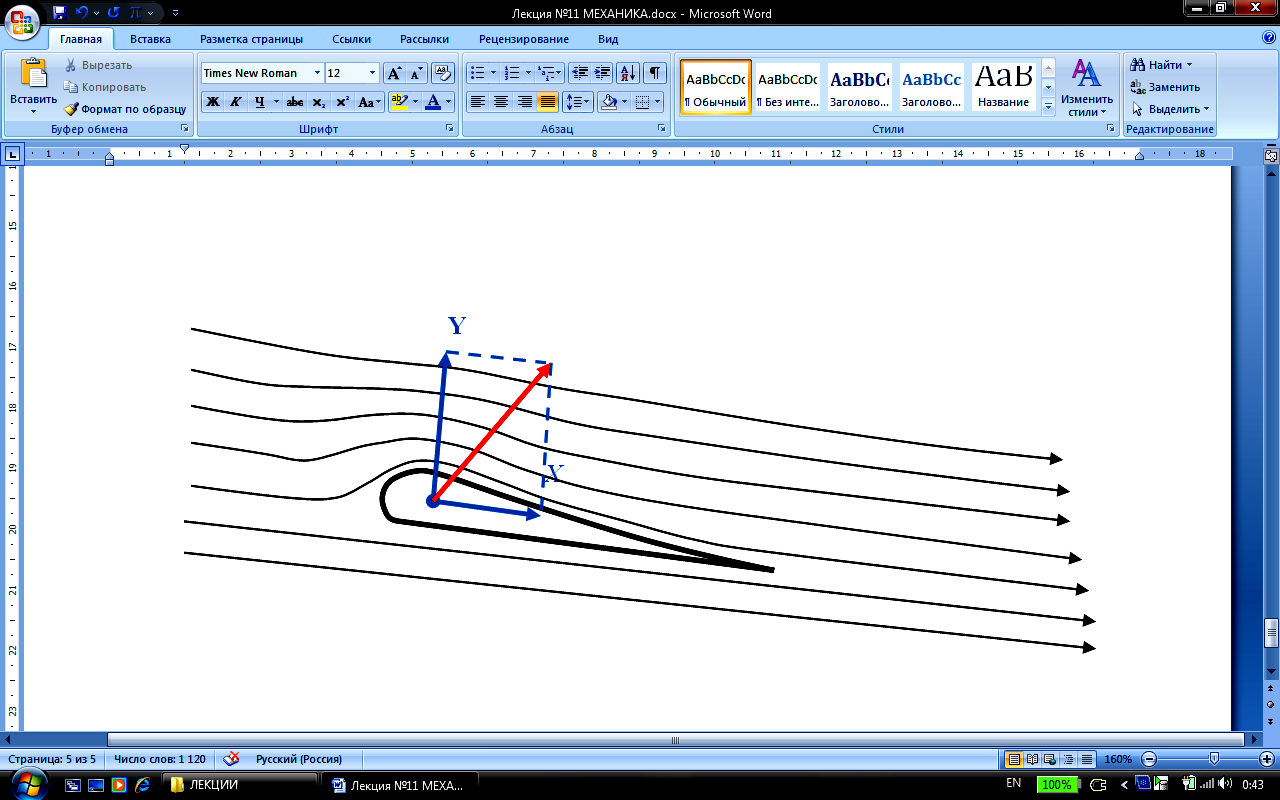
При выяснении сил, действующих на тело, безразлично, что считать движущимся – тело или среду. Удобно предполагать тело неподвижным, а среду движущейся.

Силу , с которой набегающий поток действует на тело, можно разложить на две составляющие: направленную вдоль скоростиневозмущённого потока силу, называемуюлобовым сопротивлением, и перпендикулярную к силу, называемуюподъёмной силой. На тело, симметричное относительно направления скорости , может действовать только сила лобового сопротивления, подъёмная же сила будет отсутствовать.

Подъёмная сила крыла самолёта:

В несжимаемой идеальной жидкости равномерное движение тела произвольной формы должно было бы происходить без лобового сопротивления (парадокс Даламбера).

Стокс (Джордж Габриэль Стокс 1819-1903 гг. – английский физик и математик) установил, что при небольших скоростях и размерах тел (при малых Re) модуль силы сопротивления определяется формулой , гдеη – динамическая вязкость, l – характерный размер тела, υ – модуль скорости тела, k – коэффициент пропорциональности, зависящий от формы тела.

Модуль силы сопротивления, действующей на небольшие шарики, движущиеся в жидкости, при малых скоростях определяется формулой:

- формула Стокса,

где r – радиус шарика.