ГОС / 38

38. Опыты по дифракции микрочастиц не дает основания считать, что вещество частицы распределено в пространстве в соответствии с амплитудами волны де Бройля. При изменении интенсивности падающего пучка на экране наблюдаются отдельные вспышки, что наблюдалось как для частиц, так и для волн.

Другая интерпретация опытов по дифракции состоит в том, что волна де Бройля имеет вероятностную природу. Максимум амплитуды волны де Бройля совпадает с максимумом вероятности обнаружить частицу в данном месте, а совокупность дифракционных максимумов – это совокупность максимумов вероятности обнаружения частицы, имеющей определенный импульс и энергию.

Вероятность обнаружить частицу для любой области одинакового объема одинакова, т.е. точно задавая импульс частицы, приходим к полной неопределенности координаты и наоборот.

Волновая функция.

В основе квантово-механического описания состояния микрообъектов лежит понятие вектора состояний.

В координатном пространстве вектор состояний представляет собой волновую функцию.

Рассмотрим микрочастицу. Пусть она находится в элементе объема dV=dxdydz.

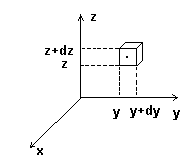
Пусть она имеет определенный импульс. Вероятность обнаружить частицу в элементарном объеме пропорциональна самому объему dV.

Вероятность обозначается W, значит dW~dV.

В квантовой механике состояние микрообъектов описывается волновой функцией в координатном пространстве, зависящей от координат и времени так, что вероятность обнаружить частицу в элементарном объеме равна:

(7.1)

Разделим (7.1) на dV: (7.2) - мы получили вероятность обнаружить частицу в данной точке пространства, окруженной единичным объемом, которая называется плотностью вероятности. Такое толкование волновой функции дал М.Борн.

Простейшей волновой функцией является волна де Бройля.

(7.3)

- это плоская монохроматическая волна, имеющая , ,, которая, согласно де Бройлю, отождествляется с частицей, энергия которой E и импульс p и. Вычислим плотность вероятности волны де Бройля:

(7.4)

,т.е. плотность вероятности волны де Бройля есть постоянная величина и равна А. Это означает, что вероятность обнаружить частицу в любой точке пространства, окруженной единичным объемом, одинакова. А это значит, что, точно задавая импульс, мы приходим к полной неопределенности координаты. Сама волновая функция физического смысла в себе не несет, т.к. комплексна. А смысл имеет квадрат модуля волновой функции. Рассмотрим конечный объем. Пусть частица находится в этом конечном объеме V. Данный объем можно разбить на бесконечное множество конечных объемов.

dV₁

dV₂

Т.к. частица находится в объеме или , или .

Как мы знаем из формулы

Вероятность нахождения частицы в объеме V определяется сложением несовместных событий.

.

Если , т.е. рассматривать все пр-во:

А то, что частицы находятся во всем пространстве, есть достоверное событие, значит

(7.5) – условие нормировки для волновой функции.

Можно убедиться, что для волны де Бройля условие нормировки не выполнимо.

Мы знаем, что волна де Бройля описывает свободную частицу с определенным импульсом. Импульс и энергия свободной частицы непрерывны. Это значит, что они имеют непрерывный спектр значений. Дирак показал, что волновые функции непрерывного спектра необходимо нормировать не на единицу, а на - функцию.

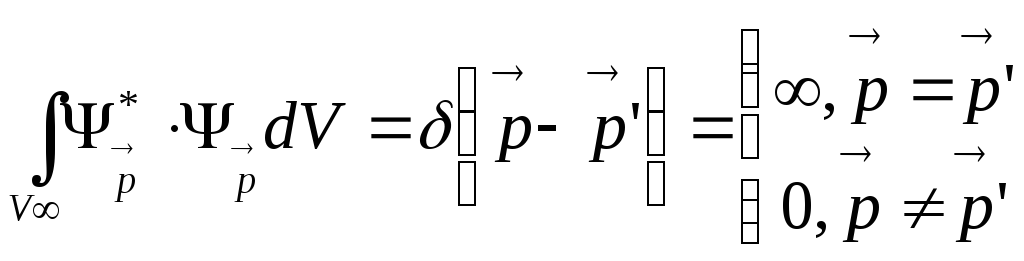
- условие нормировки функций непрерывного спектра.

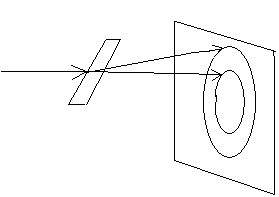
В опытах по дифракции микрочастиц, в частности в опытах Тартаковского – Томсона, первоначальный пучок электронов с определенным импульсом p расщеплялся на ряд дифрагирующих пучков, каждый из которых описывал состояние электронов с определенным импульсом .

Мы знаем, что в квантовой механике состояние микрочастицы описывается волновыми функциями, т.е. при электроны описываются - волновой функцией, - ,…, -.

Если частица может находиться в состоянии и или … , то она может находиться в состоянии, являющемся суперпозицией всех возможных состояний и описываться функцией:

(8.1)

(8.2)

Опишем мысленный эксперимент, подтверждающий принцип линейной суперпозиции – интерференция микрочастиц на 2-х щелях.

Источником термоэлектронов может служить, например, нить накала. Пропустим пучок термоэлектронов через диафрагму малого диаметра, чтобы создать точечный источник. Поместим на пути термоэлектронов 2 щели.

Получим на экране Э интерференционную картину с центральным максимумом против основного направления пучка.

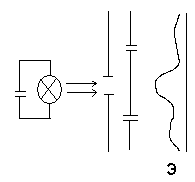
Если закрыть 2-ю щель, то появиться картина интерференции с максимумом напротив 1-й щели, аналогично, если закрыть 1-ю щель. Если сложить картинки , то на экране появиться некая плавная картина.

Интенсивность пятна при закрытой щели в 4 раза меньше максимума при 2-х открытых щелях.

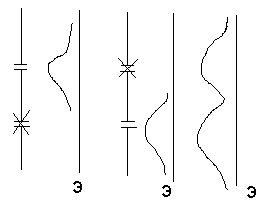
Распределение электронов на экране при закрытой 2-й щели описывается при закрытой 1-й щели, при закрытой 2-й щели, при 2-х щелях: .

Вопрос: Как считать эту плотность вероятности: Либо складывать плотности вероятности и , либо сначала складывать волновые функции, а потом

возводить модуль в квадрат. Эксперимент показывает, что складывать плотность вероятностей при закрытии одной из щелей, то получается плавная картина, не имеющая ярко выраженных минимумов.

Если же мы сначала сложим -функции, то:

Минимумы могут получиться за счет перекрестных слагаемых и , т.е. мысленный эксперимент говорит о том, что если мы откроем 2 щели, то получается картина такого вида, что её необходимо описывать сложением сначала волновых функций, т.е. справедлив принцип линейной суперпозиции.

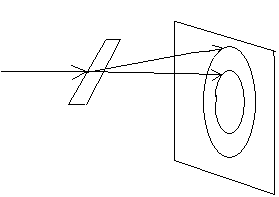
В опытах по дифракции микрочастиц каждый из дифрагируемых пучков представляет собой совокупность электронов, движущихся с определенным импульсом, и тогда эта совокупность описывается волной де Бройля.

(9.1)

Для волновой функции справедлив принцип линейной суперпозиции: Если частица может находиться в состоянии, описываемом функцией (т.е. в состоянии с импульсом ) или в состоянии, описываемом или и т.д. , то она может находиться в состоянии, являющемся линейной суперпозицией этих состояний:

(9.2)

(9.2’)

Выражения (9.2) и (9.2’) справедливы для дискретного спектра, т.е. если импульс принимает дискретный ряд значений. Если же импульс меняется непрерывно, то от суммирования переходим к интегрированию:

(9.3)

(9.3’)

Выражение принципа линейной суперпозиции представляет выражение в виде разложения по плоским волнам де Бройля.

(dp_xdp_ydp_z) – элемент импульсного пространства.

C(p) – это коэффициенты разложения.

Выясним смысл коэффициентов разложения. Для этого воспользуемся принципом линейной суперпозиции для дискретного спектра и вычислим плотность вероятности функции.

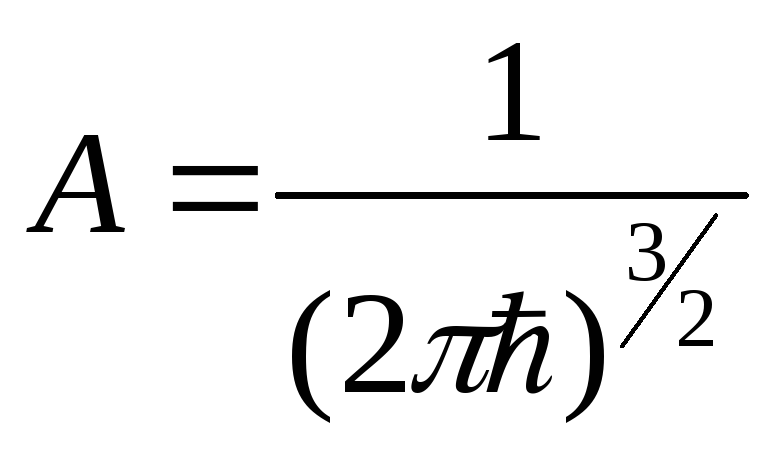- нормировочный коэффициент.

(9.4)

В первой части (9.4) стоит плотность вероятности, т.е. вероятность обнаружить частицу в единичном объеме; Следовательно, правая часть имеет также вероятностный смысл. Если предположить, что - есть вероятность обнаружить частицу в состоянии с импульсом p_i, то получаем правильную интерпретацию опытов по дифракции микрочастиц (в частности, опытов Тартаковского-Томсона).

Вероятность того, что электрон окажется в дифракционной картине определяется суммой вероятностей того, что электрон окажется в каждом дифракционном пучке. Следовательно, “” является также волновой функцией, но не в координатном, а в импульсном пространстве, причем она также подчиняется условию нормировки:

Итак, микрообъекты в квантовой механике можно описывать с помощью координатного или импульсного пространства. В координатном пространстве волновая функция зависит от координат, а в импульсном – от импульса. Квадрат модуля волновых функций – это вероятность обнаружить частицу в единице объема координатного или импульсного пространства и обе волновые функции удовлетворяют условию нормировки. Следовательно, квантовая механика работает с неполным числом переменных: вместо 6 - 3 по сравнению с классической. Следовательно, квантовая механика является менее полной по сравнению с классической и в своем описании использует элементы теории вероятностей. В квантовой механике среднее значение физических величин, зависящих от импульса, можно вычислить в координатном пространстве с помощью волновых функций координатного пространства, если физической величине: импульсу или функциям, зависящим от импульса, ставить в соответствие операторы.

Операторы, ставящиеся в соответствие физическим величинам, будем обозначать теми же буквами, но со знаком оператора:

(10.7)

(у импульсов недолжно быть операторов)

, где

Проекции импульса тоже операторы в квантовой механике:

Все физические величины, зависящие от импульса, тоже становятся операторами:

,

- лапласиан в сферической системе координат.

-оператор полной энергии - гамильтониан

В квантовой механике состояние микрообъектов описывается волновой функцией, а физические величины, характеризующие состояние микрообъектов, изображаются операторами, действующими на волновые функции.

Рассмотрим состояние микрообъекта в котором некоторая физическая величина может принимать определенное значение. Это означает, что дисперсия такой величины равна нулю.

3.1

Тогда согласно выражению 2.4

3.2

Область интегрирования выбиралась нами произвольно, следовательно,подынтегральное выражение равно нулю.

3.3

Это значит, что

3.4

3.5

Уравнение 3.5 математически есть уравнение на собственные функции и собственные значения данного оператора. В этом уравнении функции являются собственными функциями оператора , является собственными значениями данного оператора.

Данное уравнение говорит о том, что оператор , действуя на волновую функцию , дает туже самую функцию , умноженную на число . Поэтому функция является собственной функцией, а собственное значение оператора.

В квантовой механике каждой физической величине ставится в соответствии оператор. Собственное значение оператора- это же значения физической величины, которые мы наблюдаем в опыте. Поэтому реально линейный самосопряженный оператор имеет не одно собственное значение и одну собственную функцию, а бесконечно много.

Поэтому знак среднего у собственного значения ставить не будем и 3.5 запишем в виде:

3.5’

Собственные значения оператора могут принимать, как непрерывный спектр значений, так и дискретный спектр значений. Если каждому собственному значению оператора соответствует своя волновая функция, то такие собственные значения оператора, называется невырожденным.

Поэтому у волновой функции ставим : .

Однако иногда одному собственному значению соответствует несколько волновых функций. В этом случае говорят, что данное собственное значения значение оператора вырождено.