Многоканальная смо с ожиданиями

Рассмотрим многоканальную систему массового обслуживания с ожиданиями (число каналов равно n), в которой предусмотрены m мест в очереди на обслуживание. В СМО поступает поток заявок с интенсивностью λ.

Интенсивность обслуживания μ одним каналом одной заявки также известна. Необходимо найти вероятности всех состояний системы и ее показатели эффективности. Пронумеруем состояния системы по числу заявок, связанных с системой, т. е. учитываем и заявки, которые уже обслуживаются, и заявки, которые только ожидают обслуживания, т. е. стоят в очереди:

– S₀ – все каналы свободны и ни одной заявки не стоит в очереди;

– S₁ – 1 канал занят, очереди нет;

– S_к – k каналов занято, очереди нет;

– S_n – n каналов занято, очереди нет;

– S_n+1 – n каналов занято, одна заявка стоит в очереди;

– S_n+m – n каналов занято, m заявок стоят в очереди.

Изобразим граф состояния данной СМО (рис. 10).

Рис. 10

Таким образом, заявки будут поступать в систему массового обслуживания до тех пор, пока не будут заняты все каналы и все места в очереди. Если заявка прейдет в систему и застанет ее в состоянии S_n+m, то она покидает систему не обслуженной. Определим показатели эффективности многоканальной СМО:

• вероятность того, что заявка получит отказ и покинет систему не обслуженной Р_отк;

• абсолютную пропускную способность А;

• относительную пропускную способность Q;

• число занятых каналов ,

• среднее число заявок в очереди ,

• среднее число заявок, связанных с СМО, .

Для того, чтобы рассчитать характеристики, необходимо сначала найти вероятности всех состояний системы. для этого воспользуемся формулами Эрланга:

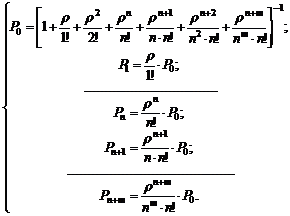(52) при этом – это приведенная интенсивность, она равна отношению интенсивности поступления заявок к интенсивности обслуживания μ. Вероятность отказа есть не что иное, как вероятность того, что поступившая в систему заявка найдет ее в состоянии S_n+m, т. е. все каналы и места в очереди заняты, следовательно, Р_отк равна P_n+m, которую мы уже нашли [см. (52)].

(53) Событие, состоящее в том, что заявка, поступившая в систему, будет обслужена или хотя бы встанет в очередь на обслуживание, является противоположным событию S_{n + m}, следовательно, его вероятность будет равна

(54) Зная относительную пропускную способность системы, легко можно найти абсолютную пропускную способность по следующей формуле

. (55) Определим среднее число занятых каналов. Каждый канал в среднем в единицу времени обслуживает μ заявок. Вся СМО обслуживает А заявок, тогда

. (56) Среднее число заявок в очереди можно вычислить непосредственно как математическое ожидание дискретной случайной величины, т. е.

. (57) Среднее число заявок, связанных с системой, т. е. заявки, которые уже обслуживаются, и те, которые еще стоят в очереди и ждут обслуживания, получим как сумму числа занятых каналов и среднего числа заявок в очереди :

(58)

Смо с отказами

Система Эрланга

В качестве показателей эффективности СМО с отказами будем рассматривать:

А — абсолютную пропускную способность СМО, т.е. среднее число заявок, обслуживаемых в единицу времени;

Q — относительную пропускную способность, т.е. среднюю долю пришедших заявок, обслуживаемых системой;

P_отк. — вероятность отказа, т.е. того, что заявка покинет СМО необслуженной;

—среднее число занятых каналов (для многоканальной системы).

Одноканальная система с отказами . Рассмотрим задачу. Имеется один канал, на который поступает поток заявок с интенсивностью λ. Поток обслуживаний имеет интенсивность μ₁. Найти предельные вероятности состояний системы и показатели ее эффективности. Система S (СМО) имеет два состояния: S₀ — канал свободен, S₁ — канал занят. Размеченный граф состояний представлен на рис. 11.

Рис. 11

В предельном, стационарном режиме система алгебраических уравнений для вероятностей состояний имеет вид. (59) т.е. система вырождается в одно уравнение. Учитывая нормировочное условие p₀+p₁=1, найдем из (59) предельные вероятности состояний

(60) которые выражают среднее относительное время пребывания системы в состоянии S₀ (когда канал свободен) и S₁ (когда канал занят), т.е. определяют соответственно относительную пропускную способность Q системы и вероятность отказа P_отк: (61)  (62) Абсолютную пропускную способность найдем, умножив относительную пропускную способность Q на интенсивность потока отказов   (63) 

Задача 5. Известно, что заявки на телефонные переговоры в телевизионном ателье поступают с интенсивностью λ, равной 90 заявок в час, а средняя продолжительность разговора по телефону_об.=2 мин. Определить показатели эффективности работы СМО (телефонной связи) при наличии одного телефонного номера. Решение.

Имеем λ=90 (1/ч),_об.=2 мин.

Интенсивность потока обслуживании μ=1/_об=1/2=0,5 (1/мин)=30 (1/ч).

По (61) относительная пропускная способность СМО: Q=30/(90+30)=0,25, т.е. в среднем только 25% поступающих заявок осуществят переговоры по телефону. Соответственно вероятность отказа в обслуживании составит Р_отк.=0,75 (см. (62)). Абсолютная пропускная способность СМО по (63), A=90∙0,25=22,5, т.е. в среднем в час будут обслужены 22,5 заявки на переговоры. Очевидно, что при наличии только одного телефонного номера СМО будет плохо справляться с потоком заявок.

Многоканальная система с отказами . Рассмотрим классическую задачу Эрланга. Имеется n каналов, на которые поступает поток заявок с интенсивностью λ. Поток обслуживаний имеет интенсивность μ. Найти предельные вероятности состояний системы и показатели ее эффективности.

Система S (СМО) имеет следующие состояния (нумеруем их по числу заявок, находящихся в системе): S₀, S₁, S₂, …, S_k, …, S_n, где S_k — состояние системы, когда в ней находится k заявок, т.е. занято k каналов.

Граф состояний СМО соответствует процессу гибели и размножения и показан на рис. 12. Рис. 12

Поток заявок последовательно переводит систему из любого левого состояния в соседнее правое с одной и той же интенсивностью λ. Интенсивность же потока обслуживаний, переводящих систему из любого правого состояния в соседнее левое состояние, постоянно меняется в зависимости от состояния. Действительно, если СМО находится в состоянии S₂ (два канала заняты), то она может перейти в состояние. S₁ (один канал занят), когда закончит обслуживание либо первый, либо второй канал, т.е. суммарная интенсивность их потоков обслуживании будет 2μ. Аналогично суммарный поток обслуживаний, переводящий СМО из состояния S₃ (три канала заняты) в S₂. будет иметь интенсивность Зμ, т.е. может освободиться любой из трех каналов и т.д. В формуле (16) для схемы гибели и размножения получим для предельной вероятности состояния (64) где члены разложения будут представлять собой коэффициенты при p₀ в выражениях для предельных вероятностей p₁, p₂, …, p_k, …, p_n. Величина   (65) называется приведенной интенсивностью потока заявок или интенсивностью нагрузки канала. Она выражает среднее число заявок, приходящее за среднее время обслуживания одной заявки.

Теперь (66) (67) Формулы (66) и (67) для предельных вероятностей получили названия формул Эрланга в честь основателя теории массового обслуживания.

Вероятность отказа СМО есть предельная вероятность того, что все n каналов системы будут заняты, т.е.

(68) Относительная пропускная способность — вероятность того, что заявка будет обслужена:  (69) Абсолютная пропускная способность:

 (70) Среднее число занятых каналов есть математическое ожидание числа занятых каналов: где p_k — предельные вероятности состояний, определяемых по формулам (66), (67). Однако среднее число занятых каналов можно найти проще, если учесть, что абсолютная пропускная способность системы А есть не что иное, как интенсивность потока обслуженных системой заявок (в единицу времени). Так как каждый занятый канал обслуживает в среднем μ заявок (в единицу времени), то среднее число занятых каналов  (71) или, учитывая (70), (65):

(72)