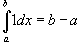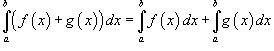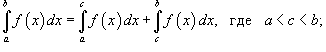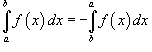23,24,25,26,30
.docx23. Понятие дифференциала функции. Свойства. Применение дифференциала в приближенных вычислениях.
Понятие дифференциала функции
Пусть функция у=ƒ(х) имеет в точке х отличную от нуля производную.
![]()
Тогда, по теореме о связи функции, ее предела и бесконечно малой функции, можно записать у/х=ƒ'(х)+α, где α→0 при ∆х→0, или ∆у=ƒ'(х)•∆х+α•∆х.
Таким
образом, приращение функции ∆у
представляет собой сумму двух слагаемых
ƒ'(х)•∆х и а•∆х, являющихся бесконечно
малыми при ∆x→0. При этом первое слагаемое
есть бесконечно малая функция одного
порядка с ∆х, так как![]() а
второе слагаемое есть бесконечно малая
функция более высокого порядка, чем ∆х:
а
второе слагаемое есть бесконечно малая
функция более высокого порядка, чем ∆х:
![]()
Поэтому первое слагаемое ƒ'(х) ∆х называют главной частью приращения функции ∆у.
Дифференциалом функции у=ƒ(х) в точке х называется главная часть ее приращения, равная произведению производной функции на приращение аргумента, и обозначается dу (или dƒ(х)):
dy=ƒ'(х)•∆х. (1)
Дифференциал dу называют также дифференциалом первого порядка. Найдем дифференциал независимой переменной х, т. е. дифференциал функции у=х.
Так как у'=х'=1, то, согласно формуле (1), имеем dy=dx=∆x, т. е. дифференциал независимой переменной равен приращению этой переменной: dх=∆х.
Поэтому формулу (1) можно записать так:
dy=ƒ'(х)dх, (2)
иными словами, дифференциал функции равен произведению производной этой функции на дифференциал независимой переменной.
Из формулы (2) следует равенство dy/dx=ƒ'(х). Теперь обозначение
производной dy/dx можно рассматривать как отношение дифференциалов dy и dх.
Дифференциал обладает следующими основными свойствами.
1. d(с)=0.
2. d(u+w-v)= du+dw-dv.
3. d(uv)=du·v+u·dv.
d(сu)=сd(u).
4. ![]() .
.
5. y=f(z), ![]() ,
, ![]() ,
,
![]() .
.
Форма дифференциала инвариантна (неизменна): он всегда равен произведению производной функции на дифференциал аргумента, независимо от того, простым или сложным является аргумент.
Применение дифференциала к приближенным вычислениям
Как уже известно, приращение ∆у функции у=ƒ(х) в точке х можно представить в виде ∆у=ƒ'(х)•∆х+α•∆х, где α→0 при ∆х→0, или ∆у=dy+α•∆х. Отбрасывая бесконечно малую α•∆х более высокого порядка, чем ∆х, получаем приближенное равенство
∆у≈dy, (3)
причем это равенство тем точнее, чем меньше ∆х.
Это равенство позволяет с большой точностью вычислить приближенно приращение любой дифференцируемой функции.
Дифференциал обычно находится значительно проще, чем приращение функции, поэтому формула (3) широко применяется в вычислительной практике.
24. Первообразная функция и неопределенный интеграл.
ПОНЯТИЕ ПЕРВООБРАЗНОЙ ФУНКЦИИ И НЕОПРЕДЕЛЕННОГО ИНТЕГРАЛА
Функция F (х)
называется первообразной
функцией для
данной функции f (х)
(или, короче, первообразной данной
функции f (х))
на данном промежутке, если на этом
промежутке
![]() . Пример.
Функция
. Пример.
Функция ![]() является
первообразной функции
является
первообразной функции ![]() на
всей числовой оси, так как
на
всей числовой оси, так как ![]() при
любом х.
Отметим,
что вместе с функцией
при
любом х.
Отметим,
что вместе с функцией ![]() первообразной
для
первообразной
для ![]() является
любая функция вида
является
любая функция вида ![]() ,
где С —
произвольное постоянное число (это
следует из того, что производная
постоянной равна нулю). Это свойство
имеет место и в общем случае.
,
где С —
произвольное постоянное число (это
следует из того, что производная
постоянной равна нулю). Это свойство
имеет место и в общем случае.
Теорема
1. Если ![]() и
и ![]() —
две первообразные для функции f (х)
в некотором промежутке, то разность
между ними в этом промежутке равна
постоянному числу.
Из
этой теоремы следует, что если известна
какая-нибудь первообразная F (х)
данной функции f (х),
то все множество первообразных для f (х)
исчерпывается функциями F (х)
+ С.
Выражение F (х)
+ С,
где F (х)
— первообразная функции f (х)
и С —
произвольная постоянная,
называется неопределенным
интегралом от
функции f (х)
и обозначается символом
—
две первообразные для функции f (х)
в некотором промежутке, то разность
между ними в этом промежутке равна
постоянному числу.
Из
этой теоремы следует, что если известна
какая-нибудь первообразная F (х)
данной функции f (х),
то все множество первообразных для f (х)
исчерпывается функциями F (х)
+ С.
Выражение F (х)
+ С,
где F (х)
— первообразная функции f (х)
и С —
произвольная постоянная,
называется неопределенным
интегралом от
функции f (х)
и обозначается символом ![]() ,
причем f (х)
называется подынтегральной
функцией ;
,
причем f (х)
называется подынтегральной
функцией ;
![]() — подынтегральным
выражением,
х — переменной
интегрирования;
∫
— знак
неопределенного интеграла.
Таким
образом, по определению
— подынтегральным
выражением,
х — переменной
интегрирования;
∫
— знак
неопределенного интеграла.
Таким
образом, по определению ![]() если
если ![]() .
Возникает
вопрос: для
всякой ли функции f (х)
существует первообразная, а значит, и
неопределенный интеграл?
Теорема
2. Если
функция f (х) непрерывна на
[a ; b],
то на этом отрезке для функции f (х) существует
первообразная.
Ниже
мы будем говорить о первообразных лишь
для непрерывных функций. Поэтому
рассматриваемые нами далее в этом
параграфе интегралы существуют.
.
Возникает
вопрос: для
всякой ли функции f (х)
существует первообразная, а значит, и
неопределенный интеграл?
Теорема
2. Если
функция f (х) непрерывна на
[a ; b],
то на этом отрезке для функции f (х) существует
первообразная.
Ниже
мы будем говорить о первообразных лишь
для непрерывных функций. Поэтому
рассматриваемые нами далее в этом
параграфе интегралы существуют.
25. Свойства неопределенного интеграла. Интегралы от основных элементарных функций.
Свойства неопределенного интеграла
В приведенных ниже формулах f и g - функции переменной x, F - первообразная функции f, а, k, C - постоянные величины.
![]()
![]()
![]()
![]()
Интегралы элементарных функций
Список интегралов от рациональных функций
![]() (первообразная
от нуля есть константа, в любых пределах
интегрирования интеграл от нуля равен
нулю)
(первообразная
от нуля есть константа, в любых пределах
интегрирования интеграл от нуля равен
нулю)
![]()
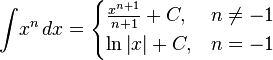
![]()
Список интегралов от логарифмических функций
![]()
![]()
![]()
Список интегралов от экспоненциальных функций
![]()
![]()
Список
интегралов от иррациональных функций![]()
![]()
![]()
![]() («длинный
логарифм»)
(«длинный
логарифм»)
список интегралов от тригонометрических функций, список интегралов от обратных тригонометрических функций
![]()
![]()
![]()
26. Метод замены переменной, метод интегрирования по частям в неопределенном интеграле.
Метод замены переменной (метод подстановки)
Метод интегрирования подстановкой заключается во введении новой переменной интегрирования (то есть подстановки). При этом заданный интеграл приводится к новому интегралу, который является табличным или к нему сводящимся. Общих методов подбора подстановок не существует. Умение правильно определить подстановку приобретается практикой.
Пусть
требуется вычислить интеграл ![]() Сделаем
подстановку
Сделаем
подстановку ![]() где
где ![]() —
функция, имеющая непрерывную производную.
—
функция, имеющая непрерывную производную.
Тогда ![]() и
на основании свойства инвариантности
формулы интегрирования неопределенного
интеграла получаем формулу
интегрирования подстановкой:
и
на основании свойства инвариантности
формулы интегрирования неопределенного
интеграла получаем формулу
интегрирования подстановкой:
![]()
Интегрирование по частям
Интегрирование по частям — применение следующей формулы для интегрирования:
![]()
Или:
![]()
В частности, с помощью n-кратного применения этой формулы находится интеграл
![]()
где ![]() —
многочлен
—
многочлен ![]() -й
степени.
-й
степени.
30. Свойства определенного интеграла. Формула Ньютона – Лейбница.
Основные свойства определенного інтеграла
Свойства определенного интеграла
-
 где k -
константа;
где k -
константа;
-
Если
 для
всех
для
всех 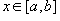 ,
то
,
то  .
.
-
Если
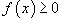 в
интервале [a,
b], то
в
интервале [a,
b], то 
Формула Ньютона – Лейбница.
Пусть функция f (x) непрерывна на замкнутом интервале [a, b]. Если F (x) - первообразная функции f (x) на[a, b], то
![]()