
- •Содержание
- •Глава 1
- •Глава 2
- •III. Заключение
- •IV. Список литературы
- •Введение
- •Глава 1
- •1.Основные понятия теории уравнений
- •1.1. Понятие уравнения
- •2. Основные понятия теории неравенств
- •2.1. Понятие неравенства
- •5. Решение уравнений и неравенств с использованием свойств входящих в них функций
- •5.1.Применение основных свойств функций
- •5.1.1. Использование одз
2. Основные понятия теории неравенств
2.1. Понятие неравенства
Пусть функции f и g заданы на некоторых числовых множествах X1 и X2.
Неравенством называется отношение вида:
f(x1, x2, …, xn) ˅ g(x1, x2, …, xn), (1)
где ˅ может обозначать любой из символов: >, <, ≥, ≤.
Далее будем использовать знак ˅, не уточняя его обозначения.
Неравенства, составленные с помощью знаков > или <, называются строгими; а неравенства, составленные с помощью знаков ≥ или ≤ – нестрогими.
Вместо двух неравенств: f(x) < g(x) и g(x) < α(x) употребляется запись:
f(x) < g(x) < α(x). Такое неравенство называется двойным.
Неравенства, содержащие только числа, называются числовыми неравенствами.
Областью допустимых значений неравенства (1) (ОДЗ) называется множество значений переменной, на котором обе части неравенства (1) определены одновременно, т.е. имеют смысл.
Другими словами, ОДЗ = X1 ∩ X2 – есть пересечение областей определения функций f и g.
Решением неравенства (1) называется некоторая система значений k1 , k2, …, kn переменных x1, x2, …, xn из ОДЗ неравенства (1), при которой данное неравенство обращается в верное числовое неравенство.
Решить неравенство – это значит найти все его решения или доказать, что их нет.
Обычно решения неравенства записываются в виде промежутка или объединения нескольких промежутков.
Упростить или решить неравенства иногда удаётся с помощью равносильных преобразований.
Равносильные неравенства
Два неравенства:
f1(x1, x2, …, xn) ˅ g1(x1, x2, …, xn) и f2(x1, x2, …, xn) ˅ g2(x1, x2, …, xn) (2) называются равносильными, или эквивалентными, если совпадают множества всех их решений. При этом пишут:
f1(x1, x2, …, xn) ˅ g1(x1, x2, …, xn) <=> f2(x1, x2, …, xn) ˅ g2(x1, x2, …, xn)
Если оба неравенства не имеют решений, то по определению они также считаются равносильными.
Например:
x2 1 <=> 1 +
 >0, так как множества решений каждого
из этих неравенств есть x
> 1 и x
< -1.
>0, так как множества решений каждого
из этих неравенств есть x
> 1 и x
< -1. x – 1 > 0 <≠> x(x – 1) > 0, так как x = -2 является решением второго неравенства, но не является решением первого.
Равносильные
неравенства могут иметь различные
области допустимых значений. Например:
неравенство x
> 1 равносильно неравенству
 >1, однако ОДЗ первого неравенства
представляет собой множество всех
действительных чисел, а ОДЗ второго –
множество неотрицательных чисел.
>1, однако ОДЗ первого неравенства
представляет собой множество всех
действительных чисел, а ОДЗ второго –
множество неотрицательных чисел.
Из определения равносильных неравенств следует, что вместо данного неравенства можно решать неравенство, ему равносильное.
Два неравенства называются равносильными на множестве A, если совпадают множества их решений, принадлежащие этому множеству A.
Два неравносильных неравенства могут быть равносильными на некотором множестве. Например: неравенства x2 > 1 и x > 1, которые равносильны на множестве положительных чисел, не являются равносильными на множестве всех действительных чисел.
Если для данной пары неравенств (2) любое решение первого неравенства является решением второго неравенства, то второе неравенство называется следствием первого неравенства. При этом пишут:
f1(x1, x2, …, xn) ˅ g1(x1, x2, …, xn) => f2(x1, x2, …, xn) ˅ g2(x1, x2, …, xn).
Если заменить неравенство его следствием, то множество решений второго неравенства будет содержать множество решений исходного неравенства и помимо него может содержать некоторые числа, называемые посторонними решениями исходного неравенства. Поэтому, если в процессе решения от неравенства переходят к его следствию, то в конце решения необходимо провести исследование, позволяющее из полученного множества чисел отобрать те из них, которые являются решениями исходного неравенства.
Например: x2
< x
+ 1 => x
<

Множество
решений неравенства x2
< x
+ 1 состоит из всех чисел промежутка ( ;
;
 ),
однако
множество решений неравенства x
<
),
однако
множество решений неравенства x
<
 состоит из всех чисел промежутка[1;
состоит из всех чисел промежутка[1;
 ).
).
Этот пример, в частности, показывает, что посторонние решения (для исходного неравенства) могут возникнуть даже тогда, когда происходит сужение (а не расширение) области допустимых значений исходного неравенства.
Чаще всего посторонние решения при замене одного неравенства другим происходят за счет расширения ОДЗ исходного неравенства.
Утверждения о равносильности неравенств:
Неравенства f(x) < g(x) <=> g(x) > f(x) (свойство необратимости неравенств: при перестановке правой и левой частей неравенства смысл знака неравенства изменяется на противоположный).
Неравенства f(x) < g(x) <=> f(x) - g(x) < 0.
Неравенства f(x) < g(x) <=> f(x) + α(x) < g(x) + α(x), если функция α(x) определена на ОДЗ неравенства f(x) < g(x).
В частности, неравенства f(x) < g(x) <=> f(x) + α < g(x) + α, где α - ∀ число (закон монотонности сложения: к обеим частям неравенства можно прибавить поровну).
f(x) < g(x) <=> α(x)f(x) < α(x)g(x), если функция α(x) > 0 при всех x из ОДЗ неравенства f(x) < g(x).
f(x) < g(x) <=> α(x)f(x) > α(x)g(x), если функция α(x) < 0 при всех x из ОДЗ неравенства f(x) < g(x).
В частности, если α > 0, то f(x) < g(x) <=> α f(x) < α g(x),
если α < 0, то f(x) < g(x) <=> α f(x) > α g(x).
Эти операции выполняются по закону монотонности умножения: при умножении обеих частей неравенства на положительный множитель смысл знака неравенства не меняется, а при умножении на отрицательный множитель смысл знака неравенства изменяется на противоположный.
 >
0
<=>
f(x)g(x) > 0.
>
0
<=>
f(x)g(x) > 0.f(x) > g(x) <=> af(x) > ag(x) для∀ фиксированного числа a (1; + ).
f(x) > g(x) <=> af(x) < ag(x) для∀ фиксированного числа a (0; 1).
Пусть функции f(x) и g(x) – неотрицательны на некотором множестве А. Тогда на этом множестве неравенства:
f(x) > g(x) <=> f n(x) > g n(x) (n N).
f(x) < g(x) <=>
 <
<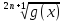 (n
N).
(n
N).|f(x)| < |g(x)| <=> f 2n(x) < g 2n(x) (n N).
f(x) < g(x) <=> f 2n(x) < g 2n(x) (n N), если f(x) и g(x) – положительные функции.
Пусть a – фиксированное число (1; + ), и функции f(x) и g(x) – положительны на некотором множестве А. Тогда на этом множестве неравенства:
f(x) > g(x) <=> log a f(x) > log a g(x).
Пусть a – фиксированное число (0; 1), и функции f(x) и g(x) – положительны на некотором множестве А. Тогда на этом множестве неравенства:
f(x) > g(x) <=> log a f(x) < log a g(x).
Утверждения о следствии:
f(x) < g(x) < α(x) => f(x) < α(x) (свойство транзитивности неравенств).
f(x) < g(x) и φ(x) < α(x) => f(x) + φ(x) < g(x) + α(x) (неравенства одинакового смысла можно складывать почленно).
f(x) < g(x) и φ(x) > α(x) => f(x) - φ(x) < g(x) - α(x) (неравенства противоположного смысла можно вычитать почленно).
f(x) < g(x) и φ(x) < α(x) => f(x)φ(x) < g(x)α(x), если функции f, g, φ и α – положительные (неравенства одинакового смысла с положительными частями можно почленно перемножать).
f(x) < g(x) и φ(x) < α(x) => f(x)φ(x) > g(x)α(x), если функции f, g, φ и α – отрицательные (неравенства одинакового смысла с отрицательными частями можно почленно перемножать, изменив при этом смысл знака неравенства на противоположный).
f(x) + α(x) < g(x) + α(x) => f(x) < g(x).
f(x) < g(x) => f n(x) < gn(x) (n N), если f(x) и g(x) – положительные функции (обе части неравенства с положительными членами можно возвести в оду и ту же степень).
 <
<
 (n
N) => f(x) < g(x).
(n
N) => f(x) < g(x).Пусть a – фиксированное число (1; + ). Тогда:
log a f(x) < log a g(x) => f(x) < g(x).
Пусть a – фиксированное число (0; 1). Тогда:
log a f(x) < log a g(x) => f(x) > g(x).
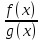 >
0
=>
f(x)
> 0, где g(x)
≥ 0.
>
0
=>
f(x)
> 0, где g(x)
≥ 0.
Тождественные неравенства
Пусть f(x1, x2, …, xn) и g(x1, x2, …, xn) – некоторые аналитические выражения, заданные совместно (на одном и том же множестве).
Неравенство f(x1, x2, …, xn) ˅ g(x1, x2, …, xn) выполняется тождественно, если оно имеет место для значений f и g при произвольных допустимых системах значений аргументов.
Под доказательством неравенства обычно понимают доказательство утверждения, что данное неравенство выполняется тождественно при всех системах допустимых значений, входящих в него аргументов.
Общих способов доказательства неравенств установить невозможно ввиду большого разнообразия как самих неравенств, так и применяемых в доказательствах методов.
Классификация неравенств
Так же, как и уравнения, неравенства делятся на алгебраические и трансцендентные.
Неравенство (1) называется алгебраическим, если функции f и g представляют собой многочлены.
Эти неравенства в свою очередь подразделяются на:
Линейные неравенства (ax + b ˅ cx + d).
Квадратичные неравенства (a1x2 + b1x + c1 ˅ a2x2 + b2x + + c2).
Неравенства высших степеней.
Неравенство (1) называется трансцендентным, если, по крайней мере, одна из функций f и g – трансцендентная.
В зависимости от того, какая функция f или g – показательная, логарифмическая или тригонометрическая, трансцендентные неравенства классифицируются на:
Показательные неравенства:
ax ˅ b; a1x ˅ a2x, где a > 0, a ≠ 1, b > 0.
Логарифмические неравенства:
log a x ˅ b, где a > 0, a ≠ 1, x >0;
log a x ˅ log b x, где a, b > 0; a, b ≠ 1, x > 0.
Тригонометрические неравенства и им обратные:
sin x ˅ a, arcsin x ˅ a,
cos x ˅ a, arcos x ˅ a,
tg x ˅ a, arctg x ˅ a,
ctg x ˅ a, arcctg x ˅ a.
Кроме того, алгебраические неравенства могут быть дробно-рациональными и иррациональными.
Неравенства, в которых левая и/или правая части являются дробными рациональными выражениями, называются дробно-рациональными. (
 ˅ 0).
˅ 0).Иррациональным неравенством называется неравенство вида:
f(x1, x2, …, xn) ˅ 0, где f – иррациональная функция от неизвестных.
Неравенства делятся по числу неизвестных на:
Неравенства с одним неизвестным.
Неравенства с несколькими неизвестными.
Отдельно выделяются неравенства, содержащие модуль:
|f(x)| ˅ g(x)
|f(x)| ˅ |g(x)|.
Основные способы решения уравнений и неравенств
Основные методы решения уравнений:
Самый распространённый – метод разложения на множители;
Метод оценки областей значений выражений, входящих в уравнения.
В школе, независимо от профиля, все изучают следующие методы решения неравенств:
Решение линейных неравенств;
Решение квадратных неравенств;
Метод интервалов для многочленов и рациональных функций.
Многие школьники после изучения метода интервалов и квадратичные неравенства решают этим методом.
Но помимо вышеперечисленных способов решения неравенств есть и другие, применимые и для решения уравнений:
Метод замены переменных;
Применение равносильности и её утверждений;
Метод понижения степени, с помощью формул приведения и основного тригонометрического тождества (для тригонометрических уравнений и неравенств).
Не будем подробно останавливаться на каждом из этих методов, так как наш главный способ заключается в применении свойств функций, входящих в уравнения и неравенства.
Элементарные функции и их свойства
Понятие элементарных функций
Для начала определимся с понятием функции и элементарной функции в целом.
Переменная величина y – есть функция переменной величины x в некотором числовом отрезке [a,b], если каждому значению переменной величины x, принадлежащему этому отрезку, соответствует вполне определенная величина переменной y, причем совершенно неважно, каким именно способом установлено это соответствие. y = f(x) – заданная функция.
Элементарными
функциями
называют функции вида, или функции,
заданные с помощью терма: C,
x,
 ,
ln
x,
sin
x,
arcsin
x
– базовые элементарные функции, а также
функции вида: f
±
g,
fxg,
f
ᵒ
g
(сложная функция), где f
и g
– базовые элементарные функции.
,
ln
x,
sin
x,
arcsin
x
– базовые элементарные функции, а также
функции вида: f
±
g,
fxg,
f
ᵒ
g
(сложная функция), где f
и g
– базовые элементарные функции.
Основные свойства элементарных функций
К основным свойствам элементарных функций относятся:
Область определения.
Областью определения функции (Df) называется множество всех допустимых значений x, при которых формула имеет смысл.
Т.е. если у нас есть функция y = f(x), то Df = {x X | y $ y = f(x)}.
Для аналитического выражения существует понятие ОДЗ. Что касаемо функции y = f(x), то ОДЗ – это область допустимых значений выражения, находящегося в правой части равенства y = f(x). ОДЗ выражения f(x) – это и есть область определения функции y = f(x).
Множество значений.
Множеством значений функции (Ef) называется множество всех тех элементов y, для которых выполняется y = f(x).
Т.е. Ef = {y Y | y = f(x), x Df }.
Чётность/нечётность.
Функция y = f(x) называется чётной, если последовательно выполняются 2 условия:
Область определения данной функции является симметричным множеством, т.е. x Df, -x Df.
Для x Df => f(-x) = f(x).
Функция y = f(x) называется нечётной, если последовательно выполняются 2 условия:
Область определения данной функции является симметричным множеством, т.е. x Df, -x Df.
Для x Df => f(-x) = - f(x).
Периодичность.
Функция y = f(x) называется периодической на множестве X, если последовательно выполняются 2 условия:
x X, (x ± T) X, где T > 0.
Для x X f(x ± T) = f(x).
Монотонность.
Функция y = f(x) называется возрастающей на числовом промежутке X, если для двух значений аргумента x1 и x2 X, причём x1 < x2, => f(x1) < f(x2).
Функция y = f(x) называется убывающей на числовом промежутке X, если для двух значений аргумента x1 и x2 X, причём x1 < x2, => f(x2) < f(x1).
Функция y = f(x) называется неубывающей на числовом промежутке X, если для двух значений аргумента x1 и x2 X, причём x1 < x2, => f(x1) ≤ f(x2).
Функция y = f(x) называется невозрастающей на числовом промежутке X, если для двух значений аргумента x1 и x2 X, причём x1 < x2, => f(x2) ≤ f(x1).
Возрастающие и невозрастающие, убывающие и неубывающие функции называются монотонными.
Возрастающие и убывающие функции – строго-монотонным
Ограниченность.
Функция y = f(x) называется ограниченной, если множество её значений представляет собой ограниченное множество.
Т.е. x Df => m ≤ f(x) ≤ M, где m, M Ef .
Непрерывность.
Функция y = f(x) называется непрерывной в точке a, если существует предел в этой точке, и он равен значению функции в этой точке.
Т.е.
 = f(a).
= f(a).
Функция y = f(x) называется непрерывной на отрезке [a,b], если она непрерывна в каждой точке интервала (a,b) и непрерывна в точке a справа, а в точке b – слева.
Отметим, что все элементарные функции непрерывны в области своего определения.
Графиком функции y = f(x) называется множество точек M(x,y) на координатной плоскости, где y = f(x), x Df.
Функции синус и косинус числового аргумента
Ранее мы упоминали, что функция вида sin x является элементарной. Дадим определение этой функции.
Синусом действительного числа t называется ордината точки на координатной окружности с круговой координатой t: sin t = y.
Координатная окружность – это окружность единичного радиуса с центром в начале прямоугольных координат, с выбранной точкой (началом) отсчёта и положительным направлением движения.
Круговая координата t точки на координатной окружности – это длина дуги с концами в этой точке и начале отсчёта.
Косинусом действительного числа t называется абсцисса точки на координатной окружности с круговой координатой t: cos t = x.
По
формуле приведения для синуса: sin
(t
+
 )
= cos
t.
)
= cos
t.
Исходя из этого, можем говорить, что функция cos числового аргумента также является элементарной.
Функции: y = sin x
y = cos x
имеют одинаковые области определения и множества значений:
Df = {x (-; +)},
Ef = {y [-1;1]}.
При решении уравнений нам понадобятся следующие свойства:
Синуса: если для некоторого числа x0 справедливо строгое неравенство |sin ax0| < 1, то такое число не может быть корнем ни одного из уравнений:
sin αx sin βx = ± 1,
sin αx cos βx = ± 1,
A(sin αx)m + B(cos βx)n = ± (|A| + |B|),
A(sin αx)m + B(sin βx)n = ± (|A| + |B|),
где α, β, A и B – данные действительные числа, n и m – данные натуральные числа.
Косинуса: если для некоторого числа x0 справедливо строгое неравенство |cos ax0| < 1, то такое число не может быть корнем ни одного из следующих уравнений:
cos αx cos βx = ± 1,
A(cos αx)m + B(cos βx)n = ± (|A| + |B|),
где α, β, A и B – данные действительные числа, n и m – данные натуральные числа.
Доказательство:
Если число меньше 1, то произведение его на ему подобное не даст число, равное единице.
Это возможно, если только мы умножаем на дробь, обратную данной. А обратная дробь будет > 1, что противоречит условию: |sin ax0| < 1.
Т.е. произведение двух правильных дробей даёт правильную дробь.
Значит, число x0, удовлетворяющее данному условию, не является корнем уравнения sin αx sin βx = ± 1.
Если |sin ax0| < 1 то, |cos βx0| < 1, так как sin2 ax0 + cos2 ax0 = 1.
Поэтому произведение |sin αx0 cos βx0| < 1, и число x0, удовлетворяющее данному условию, не является корнем уравнения sin αx cos βx = ± 1.
Аналогично, число x0, удовлетворяющее условию |cos ax0| < 1, не является корнем уравнения cos αx cos βx = ± 1.
Уравнение A(cos αx)m + B(cos βx)n = ± (|A| + |B|) (*)
<=> (cos αx)m = (cos βx)n = ± 1.
Если число, меньшее 1, возвести в любую степень, то получим также число, меньшее 1. Поэтому равенство A(cos αx0)m + B(cos βx0)n = ± (|A|+ + |B|) будет неверным, а значит x0, удовлетворяющее условию |cos ax0| < 1, не является корнем уравнения (*).
Аналогично x0, удовлетворяющее условию |sin ax0| < 1, не является корнем уравнения A(sin αx)m + B(sin βx)n = ± (|A| + |B|).
Уравнение A(sin αx)m + B(cos βx)n = ± (|A| + |B|) (**)
<=> (sin αx)m = (cos βx)n = ± 1.
Если |sin ax0| < 1 то, |cos βx0| < 1, так как sin2 ax0 + cos2 ax0 = 1.
Поэтому равенство A(sin αx0)m + B(cos βx0)n = ± (|A|+|B|) будет неверным также, и x0, удовлетворяющее условию |sin ax0| < 1, не является корнем уравнения (**).
