Методика решения задач по электростатике

плотностью 0e r3

-23 -

r

4

Ei

Ei

dS Ei 4 r2

r3 , (1)

откуда

0

0 3

Ei

r .

(2)

3 0

Напряженность поля в полости равна разности

напряженностей полей (2) и поля шара объемом,

занимаемым полостью:

r r ,

E

(3)

3 0

1

где r1 - радиус-вектор, проведенный из центра полости в точку наблюдения.

Учитывая, что r r1 a, получаем

		a.	(4)
E

3 0

Задача 13. Пространство заполнено зарядом с объемной

, где 0 и - положительные

константы, r – расстояние от центра данной системы. Найти модуль вектора напряженности электрического поля как функцию r. Исследовать полученное выражение при малых и больших r, т.е. при r3 1 и r3 1.

Решение:

Для нахождения напряженности воспользуемся теоремой Гаусса:

- 24 -

E E 4 r	2		dV		4 0 e r3 r2dr		4 0
							3 0
			0		0

1 e r3

(1)

Из (1) получаем напряженность электрического поля

E r	0	1 e r3 .	(2)
	3 r2
	0

При малых r разлагаем экспоненту в ряд Тэйлора и оставляем первые два члена разложения. Тогда для напряженности имеем

E	0r	.	(3)
	3 0

При больших r экспонентой можно пренебречь по сравнению с единицей:

E	0	.	(4)
	3 r2
	0

Задача 14. Имеются два тонких проволочных кольца радиуса R каждое, оси которых совпадают. Заряды колец равны qи q. Найти разность потенциалов между

центрами колец, отстоящими друг от друга на расстояние a.

www.mitht.ru/e-library

- 25 -

q

a

- q

Рис. 1.12.

Решение:

Найдем сначала потенциал поля, созданного одиночным заряженным кольцом в точке наблюдения, лежащей на оси кольца на расстоянии r от его центра.

Разобъем кольцо на элементарные отрезки длиной dl и несущие заряд dq. Потенциал поля от элементарного заряда dq в точке на расстоянии r от центра кольца равен

d		dq
					.	(1)
	4 0		R2 r2

Интегрируя (1) по всему кольцу, находим потенциал поля, созданного всем кольцом на расстоянии r от центра:

		q
				.	(2)
	4 0	R2 r2

Используя (2) и принцип суперпозиции для потенциала, найдем потенциал в центре верхнего и нижнего кольца соответственно:

							q			- 26 -			q
																	,	(3)
				1			4 0R
											4 0		R2 a2
							q					q				.		(4)
		2				4 0R
										4 0		R2 a2

Следовательно, разность потенциалов между центрами колец равна

					q			q		. (5)
	1		2
					2 0R		2 0	R2 a2

	q			1
Ответ:			1							.
	2 0 R
				1		a2
						R2

Задача 15. Найти потенциал и напряженность электрического поля в центре полусферы радиуса R, заряженной равномерно с поверхностной плотностью .

Решение:

www.mitht.ru/e-library

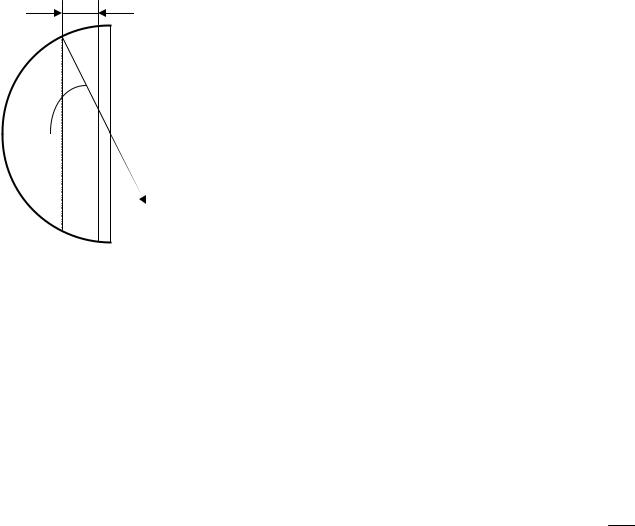
- 27 -

Rd

R

O

dE

Рис. 1.13.

Разобьем полусферу на элементарные пояса шириной R d и радиусом R sin . Площадь такого пояса равна: dS 2 Rsin Rd . (1)

Считая элементарный пояс точечным зарядом, для потенциала поля, создаваемого им в точке O , имеем:

d	dS	.	(2)
	4 0R

Согласно принципу суперпозиции для потенциала, для нахождения потенциала поля, созданного всей полусферой, необходимо проинтегрировать (2) по углу с учетом (1):

		R	/	2	sin d	R
							.	(3)
		2 0
			0			2 0

Напряженность поля элементарного пояса равна:

	- 28 -
dE	dS	.	(4)
	4 0R2

В силу симметрии вектор напряженности поля, созданного всей полусферой, будет направлен вдоль горизонтальной оси. Следовательно, надо спроецировать

(4) на эту ось и затем произвести интегрирование:

			/2
E			sin cos d					.	(5)
	2 0
			0				4 0
Ответ:		R		, E		.
			2 0		4 0

Задача 16. Найти потенциал x,y электростатического поля E 2axyi a x2 y2 j , где a – постоянная, i и

j- орты осей X и Y.

Решение:

	Ex	2axy;		Ey	a x2 y2 . (1)
x
			y

Интегрируя первое из равенств в (1) по x, получаем:

ayx2 f y const. (2)

Интегрируя второе равенство в (1) по y, имеем:

ayx2		ay	3	const ,	(3)
	3

т.е. в (2) f y ay3 .

3

www.mitht.ru/e-library

- 29 -

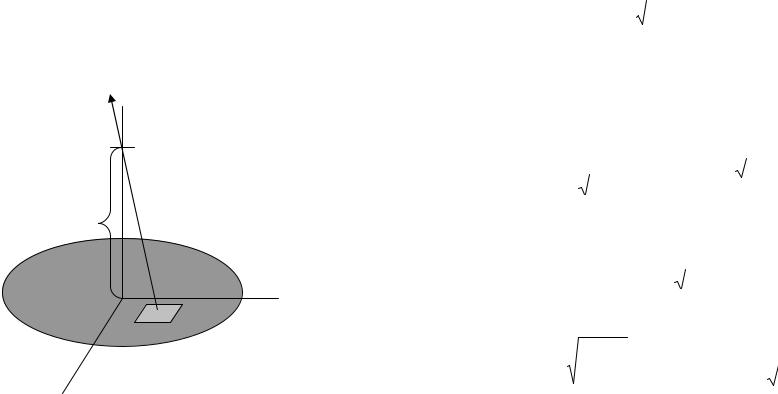
Задача 17. Находящаяся в вакууме круглая очень тонкая пластинка радиуса R равномерно заряжена с поверхностной плотностью . Найти потенциал и напряженность электрического поля на оси пластинки как функцию расстояния lот ее центра.

Исследовать полученное выражение при l 0 и l R.

Решение:

dE

Z

l

0

Y

dS

- 30 -

x, y . Считая этот элемент пластинки точечным зарядом, запишем потенциал электростатического поля, созданного им:

d		dxdy
					.	(1)
	4 0		x2 y2 z2

Перейдем от декартовых координат к цилиндрическим: x rcos , y rsin ,dxdy rdrd . (2)

Интегрируя (2) по r и , находим потенциал поля, созданного круглой пластинкой:

			R			rdr				2											. (3)
														2		2
										d			R		z				z
	4										2 0
					r	2	z	2
		0 0						0

Из соображений симметрии ясно, что вектор напряженности будет направлен вдоль оси Z, причем

d

z

z

E

z

.

(4)

dz

2 0

z

R

2

z

2

Ответ:

l

R

2

l

, E

X

1

l

2

1

1

l

2

R

2

.

2 0

2 0

При l 0потенциал

Рис. 1.14.

R

, E

; при l R потенциал

2 0

2 0

Рассмотрим элементарный прямоугольник площадью

dS = dx dy в произвольной точке пластины с координатами

q

, E

q

, где q R2 .

4

0l

4 0l2

www.mitht.ru/e-library

- 31 -

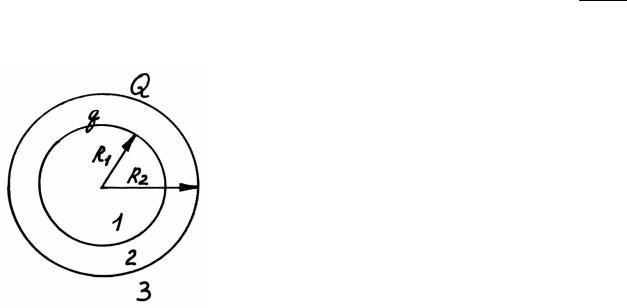
Задача 18. Система состоит из двух концентрических проводящих сфер, причем на внутренней сфере радиусом R1 находится заряд q, на внешней сфере радиусом R2 находится заряд Q. 1. Найти потенциал электрического поля во всем пространстве.

2. Каким должен быть заряд Q, чтобы потенциал внутренней сферы был равен 0? Нарисовать примерный график зависимости потенциала φ от расстояния до центра системы для этого случая, считая q<0.

Решение.

1. Решим двумя способами.

1) Рассмотрим воображаемую сферу радиусом r>R2 и найдем напряженность поля в области 3 (см. рис.) по теореме Гаусса:

Е3	4 r2	(q Q)	,	(1)
		0

Рис. 1.15.

- 32 -

	E	3		(q Q)	.
				4 0r2
							(q Q)
	Тогда потенциал в этой области 3					E3dr		.
						r	4 0r

При этом потенциал поля на бесконечности приняли за 0. Рассмотрим воображаемую сферу радиусом R1<r< R2. , тогда по теореме Гаусса найдем напряженность поля в

области 2:

E2 4 r2		q	,	(2)
		0

q

E2 4 0r2 .

Найдем потенциал поля в этой области:

R2

q

q

2 (r) 2 (R2 ) E2dr

. (3)

4 0R2

r

4 0r

Но 2 (R2 ) 3 (R2 ),.т.к. потенциал непрерывен. Значит,

2 (r)

q

q

(q Q)

q

Q

.(4)

4 0 R2

4 0R2

4 0r

4 0r

4 0R2

Внутри сферы R1 , как очевидно из теоремы Гаусса,

напряженность поля Е1

равна 0, а значит, потенциал

остается постоянным:

1

Q

q

(5)

1

2 (R1) 4

R

0

R

2

.

1

2) Воспользуемся принципом суперпозиции. Пусть - потенциал, созданный только сферой R1 , - потенциал, созданный только сферой R2 . Тогда в областях 1, 2, 3 соответственно (см. рис.)

www.mitht.ru/e-library

- 33 -

1					q			,		2											q											,				3										q			,		(6)
			4			R											4							0			r																		4		0	r
						0	1
1					Q					, 2												Q										,				3										Q				.	(7)
			4 0 R2															4 0R2																											4 0r
																1											q									Q
Тогда 1																																																			(8)
													4																						R
				1 1																		R															2			,
																					0							1
	2			2 2																q															Q																(9)
														4 0r																4 0R2
				3			3 3													(q Q)
																																	.																		(10)
																					4 0r
																					1											q								Q
2. Если 1(R1) 0											, то																																			0, откуда
																				4																				R
																										0			R														2
																																1
Q	qR2				.		Тогда
		R1
																				q								1							1
																																										,							(11)
										2					4																				R
																						0				r
																																			1
																					q															R2
																																																	(12)
										3						4										r										R
																							0						1													.
																																					1

График зависимости φ(r) для этого случая показан на рисунке.

- 34 -

Рис. 1.16.

Задача 19. Показать, что потенциал поля диполя с электрическим моментом p может быть представлен как= pr /4 0 r3 , где r – радиус-вектор. Найти с помощью этого выражения модуль вектора напряженности электрического поля диполя как функцию r и .

Er

E

r+ r-

+ q

- q

--

Рис. 1.17.

www.mitht.ru/e-library

- 35 -

- 36 -

Решение:

Потенциал электрического поля диполя в точке наблюдения на расстоянии r+ от положительного заряда и r- от отрицательного заряда равен

					q			q		.	(1)
					4	r
								4 r
						0	0

Учитывая, что длина диполя l r, находим расстояния от зарядов диполя до точки наблюдения:

r	r	lcos	,r	r	lcos	.	(2)
	2			2

Подставляя (2) в (1), получаем потенциал поля диполя:

		pr	,	(3)
		4 0r3

где p ql - электрический момент диполя.

Радиальная компонента вектора напряженности поля равна

E					pcos	.	(4)
	r
			r		2 0r3

Перпендикулярная (поперечная) компонента напряженности

E				psin	.	(5)
		r
				4 0r3

Модуль вектора напряженности электрического поля

	E				p			. (6)
		E2	E2				1 3cos2
					4 0r3
		r

www.mitht.ru/e-library

Задачи для самостоятельного решения

1.На некотором расстоянии от бесконечной равномерно заряженной плоскости с поверхностной плотностью = 0,1 нКл/см2 расположена круглая пластинка. Плоскость пластинки составляет с линиями напряженности угол 30 . Определите поток

Е вектора напряженности через эту пластинку, если ее радиус r = 0,15 м.

Ответ: Е = 3,46 кВ м.

2.Электростатическое поле создается шаром радиусом

R = 0,10 м, равномерно заряженным с объемной плотностью = 20 нКл/м3 . Определите разность потенциалов между точками, лежащими внутри шара на расстояниях r1 = 2 см и r2 = 8 см от его центра.

Ответ:				r2	r2	= 2,26 В.
			6 0
1	2			2	1

3. Найти потенциал x,y электростатического поля

E a yi xj , где a – постоянная, i и j - орты осей

X и Y.

Ответ: axy const.

4.Потенциал поля в некоторой области пространства зависит только от координатыxкак ax3 b,

где aи b- некоторые постоянные. Найти распределение объемного заряда x .

Ответ: x 6 0ax.

-37 -

5.Найти вектор напряженности электрического поля, потенциал которого имеет вид = ar, где a – постоянный вектор, r – радиус-вектор точки поля. Ответ: E = - a, т.е. поле однородное.

6.Тонкое кольцо радиуса R имеет заряд q, неравномерно распределенный по кольцу. Найти работу электрических сил при перемещении

точечного заряда q1 из центра кольца по произвольному пути в точку, находящуюся на оси кольца на расстоянии l от его центра.

	q1q		1
Ответ: A		1						.
	4 0R		1		l2
					R2

7. В вершинах квадрата со стороной a = 5 см находятся одинаковые положительные заряды Q = 2 нКл. Определите напряженность электростатического поля: 1) в центре квадрата; 2) в середине одной из сторон квадрата.

Ответ: 1) E = 0; 2) E				4Q			= 10,3 кВ/м.
	2
1			5 5			0a2

8.Находящийся в вакууме тонкий прямой стержень длины 2a заряжен равномерно зарядом q. Найти модуль вектора напряженности электрического поля как функцию расстояния r от центра стержня для точек прямой на оси стержня вне его.

Исследовать полученное выражение при r a.

	q	- 38 -
Ответ: E			.
	4 0 r2	a2

9.Положительный точечный заряд 50 мкКл находится на

плоскости xy в точке с радиус-вектором r0 = 2i + 3j, где i и j – орты осей x и y. Найти модуль и направление вектора напряженности электрического поля E в точке

с радиус-вектором r= 8i - 5j. Здесь r0 и rв метрах.

Ответ: E = 2,7i – 3,6j, E = 4,5 кВ/м.

10. Равномерно заряженная нить, на единицу длины которой приходится заряд , имеет конфигурацию, показанную на рис. Считая, что радиус закругления R значительно меньше длины нити, найти модуль вектора напряженности электрического поля в точке O.

O

R

Рис. 1.18.

Ответ: E = 0.

11.Имеется бесконечно длинная прямая нить, заряженная равномерно с линейной плотностью

www.mitht.ru/e-library

-39 -

= 0,40 мкКл/м. Вычислить разность потенциалов точек 1 и 2, если точка 2 находится в = 2,0 раза дальше от нити, чем точка 1.

Ответ:				ln = 5 кВ.
			2 0
1	2

12.Точечный заряд q находится в центре тонкого кольца радиуса R, по которому равномерно распределен заряд –q. Найти модуль вектора напряженности электрического поля на оси кольца в точке, отстоящей от центра кольца на расстояние x,

если x R.

Ответ:E		q		1				x
										;
								x2 R2	3/2
		4	0 x2
E	3qR2					при x R.
	8 0 x4

13.Найти силу взаимодействия двух молекул воды, отстоящих друг от друга на расстояние l = 10 нм, если их электрические моменты ориентированы

вдоль одной и той же прямой. Момент каждой молекулы p = 0,62 10-29 Кл м.

	Ответ: F	3p2	= 2,1 10-16 Н.
		2 0l4

-40 -

§2. Диэлектрики и проводники в электрическом поле

Вдиэлектрике электрическое смещение:

D 0E P,

где P - электрическая поляризация (вектор поляризованности), причем в изотропных диэлектриках:

P 0 E;

1,

где - диэлектрическая восприимчивость.

Связь между поверхностной плотностью 1 связанных

зарядов на границе диэлектрик – проводник и поверхностной плотностью зарядов на проводнике:

		1
	1			1 .

Задачи с решениями

Задача 1. В пространстве, наполовину заполненном парафином (ε = 2), создано однородное электрическое поле, напряженность которого в воздухе Е1 = 2 В/м. Вектор Е1 образует угол α = 60° с границей парафин - воздух, которую можно считать плоской. Определить векторы электрического смещения, напряженности и поляризации в парафине.

Решение.

www.mitht.ru/e-library

- 41 -

Рис. 2.1.

В условии задачи источник электрического поля не задан, но известны модуль и направление напряженности, а следовательно, и вектора электрического смещения в воздухе. Т. к. в воздухе D1 = ε0E1, вектор D1

параллелен вектору E1, а модуль его равен
D1 = ε0E1 = 1,77.10-11 Кл/м2.	(1)

Впарафине вектор электрического смещения связан

снапряженностью электрического поля соотношением

D2 = ε0εE2.

(2)

При этом нормальные и тангенциальные составляющие векторов (по отношению к границе диэлектрика) будут иметь вид

Dn2 = ε0εEn2 , Dτ2 = ε0εEτ2.

(3)

- 42 -

Рис. 2.2.

Так как нормальная составляющая вектора электрического смещения при переходе через границу диэлектрика не изменяется, то

Dn1 = Dn2		(4)
ε0En1 = ε0εEn2		(5)
En1 = εEn2.	составляющая	(6)
Тангенциальная		напряженности

электрического поля не терпит разрыва при переходе через границу диэлектрика, т. е.

Eτ1 = Eτ2 .

(7)

Следовательно, Dτ1 = Dτ2/ε.

Отсюда получим соотношение для модуля вектора электрического смещения

D	D2	D2		D2	2D2		.	(8)
2	n2	2		n1		1
Так как в воздухе Dn1 D1 sin ,						D 1	D1 cos ,
получаем

D D		sin2 2 cos2 2,3 10 11Кл/м2. (9)
2	1

При этом вектор D2 образует с границей раздела угол β:

www.mitht.ru/e-library