Одинцов Брук Темкин - Статистическая обработка результатов кинетических исследований

11

чет основан на использовании данных таблицы эксперимен-

та и математическое описание запишется в общем виде:

соответствующих матриц и на решении системы урав-

нений (2.7). Таблица эксперимента несколько изменится за счет введения формальных факторов:

Таблица 2.2

Но-		Значения				факторов			Результат
мер			(входов)						(выход)
опыта
									y
	x0		x1		x2	.........		xm
1	1		x11		x21	........		xm1	y1
2	1		x12		x22	.........		xm2	y2
...	1		...		...	.........			...
u	1		x1u		x2 u	.........		xmu1	yu
...	1		...		...	.........		xk 2	...
n	1		x1n		x2 n	.........		xmn	yn

Матрица факторов, векторы выходов и коэффициентов бу-

дут иметь вид:

	x		x	...	x	m1
		01	11
X	x02		x12	...	xm2
	...		...	...	...
			x1n	...
	x0m				xmn

			12
	y			b
	1			0
Y	y2		B	b1
	...			...

yn	bm
	Удалено: .	.¶
Система уравнений (2.5) очень сильно упростится за
счет членов, содержащих частные производные:

							m
f ( xiu , p j	)		f ( xiu ,bj	)			bi xi	xiu
							i 0
p j			bj				bi

Проведя эти замены перепишем систему (2.5)

	n	n	m
	yu x0u (( bi xiu )x0u ) 0
	u 1	u 1	i 0
	n	n	m
	yu x1u (( bi xiu )x1u ) 0			(2.8)
u 1		u 1	i 0
			...
n		n	m
	yu xmu (( bi xiu )xmu ) 0
u 1		u 1	i 0

Проведя простые преобразования системы (2.8), получим:

b0	n		n	n	n
	x02u	b1 x1u x0u		... bm xmu xou	yu x0u
	u 1		u 1	u 1	u 1
	n		n	n	n
b0 x0u x1u			b1 x12u	... bm xmu x1u	yu x1u	(2.9)
	u 1		u 1	u 1	u 1
				...
	n		n	n	n
b0	x0u xmu		b1 x1u xmu ... bm xmu2		yu xmu
	u 1		u 1	u 1	u 1

Удалено: ¶

Удалено: ¶

Удалено: 5) ¶

Удалено: .

Удалено: ¶

11

Можно показать, что последняя система запишется в виде матричного уравнения:

x01	x02	...	x0n		x01
	x12	...
x11			x1n	.	x02
...	...	...	...		...
	xm2	...
xm1			xmn		x0n

x	11	...	x	m1			b
							0
x12		...	xm2			.	b1
...		...	...				...
x1n		...
			xmn				bm

		x01	x02 ...
			x12 ...
		x11
		..	... ...
			xm2 ...
		xm1

или

x	0n		y
			1
x1n			. y2	.	(2.10)
...			...
xmn			yn

Решая это матричное уравнение относительно вектора ,

получим

1 1

и

		1			(2.11)

Таким образом, имея дело с линейными по коэффи-

циентам моделями сводим процедуру нахождения этих ко-

эффициентов к решению системы линейных уравнений

(2.9) , что в матричной форме запишется уравнением (2.11).

12

Решение является единственным, но определенные вычис-

лительные трудности все же остаются. Самая сложная вы-

числительная проблема при расчете по уравнению (2.11) -

это обращение матрицы ( ) (эта матрица называется

информационной матрицей, а матрица, полученная в ре-

зультате обращения - ковариационной). Точность обраще-

ния матрицы очень сильно связана с относительными значе-

ниями элементов матрицы и со структурой матрицы. По-

скольку эта матрица содержит в качестве элементов значе-

ния экспериментальных факторов, т.е. связана с условия-

ми эксперимента (значениями входов), то повлиять на ее структуру можно, поставив эксперимент определенным об-

разом. Мы приходим к идее планирования эксперимента при нахождении параметров модели. Спланировав эксперимент,

можно существенно упростить расчетные процедуры поиска коэффициентов модели, но рассмотрение этого вопроса выходит за рамки пособия.

Как уже говорилось, в задачу идентификации модели входит также получение статистических характеристик, по-

зволяющих определить адекватность модели и эксперимен-

та, а также оценить точность рассчитанных коэффициентов.

Решением этих задач занимается раздел теории статисти-

ческой обработки эксперимента - регрессионный анализ.

Удалено: ¶

Удалено: ¶

Удалено: ¶

11

2.2. Статистические характеристики модели и экс-

перимента.

2.21. Адекватность модели.

Обычная последовательность реализации метода регрессионного анализа состоит в следующем:

1.Установление наличия зависимости между входами

ивыходами.

2.Выбор класса функций, которые могли бы описать связь между входами и выходами, если установлено, что она существует(например, полином (2.6).

3.Анализ числа степеней свободы. Первоначальное число степеней свободы модели определяется как разность между числом опытов и числом коэффициентов модели: f = n - m .Чем больше опытов, тем больше информации о моде-

ли, эта информация используется для того, чтобы опреде-

лить ее коэффициенты. Отсюда ясно, что максимальное число коэффициентов модели, которое можно определить на основе проведенного эксперимента, равна числу опытов.

Но в этом случае не остается степеней свободы для нахо-

12

ждения статистических характеристик, с помощью которых можно оценить адекватность модели и оригинала. Чем больше остается степеней свободы после расчета коэффи-

циентов, тем более достоверными можно считать результа-

ты статистической обработки. Поэтому одновременно с рас-

четом каждой статистической характеристики вычисляется число степеней свободы, ей соответствующее. Используется это значение не только для качественной оценки меры дове-

рия к этой характеристике, но также при проведении оценки этих характеристик по статистическим таблицам.

4. Выбор критерия тесноты связи модели и экспери-

мента (например, сумма квадратов отклонений эксперимен-

тальных и расчетных значений).

5. Проверка адекватности. Процедура проверки адек-

ватности требует точного знания структуры модели, в на-

шем случае - порядка полинома и значений его коэффициен-

тов. Часто можно заранее оценить порядок полинома, на- Удалено: модели:¶

пример, по его графическому представлению, если это не-

возможно, то процедура проверки адекватности совмещает-

ся с процедурой выбора структуры модели. В этом случае адекватность определяется последовательно, начиная с по-

линома первой степени, имеющего наименьшее число ко-

эффициентов. Если после расчета коэффициентов проверка

11

адекватности привела к положительному результату - мо-

дель адекватна - то можно остановиться на этой структуре модели, если выбранное уравнение неадекватно, переходят к более сложной модели, добавляя новые коэффициенты, и

повторяют процедуру расчета коэффициентов и проверки адекватности.

6. Оценка значимости коэффициентов. В процедуру оценки значимости коэффициентов входит определение дисперсии коэффициентов и решение вопроса о том, име-

ет ли смысл включение этого коэффициента в уравнение модели.

Для проведения статистической обработки экспери-

мента, к последнему предъявляются определенные требо-

вания:

1. Эксперимент должен включать опыты на воспроиз-

водимость для определения дисперсии воспроизводимости.

Без определения дисперсии воспроизводимости, строго го-

воря, нельзя принять никаких решений, входящих в комплекс статистической обработки, в частности нельзя проверить адекватность модели. При строгом выполнении этого требо-

вания дисперсия воспроизводимости должна быть посчитана для каждого опыта, т.е. каждый опыт должен быть повторен несколько раз. Мало того, должна быть обеспечена равно-

12

Удалено: когда

точность эксперимента, т.е. дисперсии воспроизводимости всех опытов должны быть равны между собой. Обычно экс-

периментатор, если и повторяет опыты, то делает это для 1-

2 наиболее существенных для него опытов, а добиться рав-

ноточности практически нереально.

2. Выходные величины ( y ) должны быть нормально распределенными случайными величинами. Эксперимента-

тор практически не имеет возможности проверить это тре-

бование, но обычно считается, что оно соблюдается.

3. Ошибка в задании входных факторов ( Xi ) должна быть пренебрежимо малой по сравнению с ошибкой изме-

рения выходных величин ( y). Это требование обычно в экс-

перименте соблюдается.

Перейдем к описанию процедуры проверки адекватно-

сти модели, считая, что эти требования соблюдены или их несоблюдение можно компенсировать, либо не придать ему большого значения. Смысл проверки адекватности состоит в сравнении дисперсии воспроизводимости эксперимента,

которая отражает точность получения результатов, с так называемой остаточной дисперсией, которая характеризует тесноту связи рассчитанных по модели значений выходов со значениями, полученными экспериментально.

11

Расчет дисперсии воспроизводимости

Для расчета дисперсии воспроизводимости необходимо провести каждый опыт несколько раз, например, l раз. В общем случае число повторов в каждом опыте может быть различным, но чтобы не усложнять изложение, примем одинаковое число повторений в каждом опыте. Тогда таблица эксперимента будет выглядеть следующим образом:

Таблица 2.3

№	X0	X1	...	Xm			y			y
оп										сред
ыта										н.
1	X01	X11	...	Xm1	y11	y12		...	y1l	y1
2	X02	X12	...	Xm2	y21	y22		...	y2l	y2
...	...	...	...	...	...	...		...	...	...
n	X0n	X1n	...	Xmn	yn1	yn2		...	ynl	yn

Сначала рассчитывается среднее значение выходной вели-

чины в каждых l повторенных опытах (потратили одну сте-

пень свободы):

				l
	y			yui
		u		i 1	(2.12)
				l

12

Далее считается дисперсия воспроизводимости для каждого опыта на основе отклонений значений выхода в каждом опыте от среднего значения в этом опыте:

	l
Su2	yui		y	u 2
	i 1				,	(2.13)
		f
где f l 1 - число степеней свободы,						с учетом того, что

одна степень свободы потрачена на вычисление среднего значения.

Далее определяется среднее значение дисперсии воспроизводимости по всем опытам:

		n
	S y2	Su2		(2.14)
		u 1
		n
	Этой дисперсии соответствует число			степеней свободы

f n(l 1) - общее число опытов в эксперименте за вычетом тех, что потрачены на вычисление средних значений. Мы опускаем необходимую для строгого анализа проверку равноточности опытов, принимая, что это требование выполняется. Если же воспроизводимость анализировалась не для всех опытов, ничего не остается делать, как принять характеристику, полученную для нескольких опытов (хотя бы и для одного), в качестве характеристики всего эксперимента с соответствующим пересчетом числа степеней свободы.

11

Расчет остаточной дисперсии

Далее определяется остаточная дисперсия на основе отклонений всех экспериментальных значений выхода от расчетных значений:

	n l
	yui		2
Sост2		yu			SS		,
	u 1i 1					ост
	fост
					fост

где SSос т- сумма квадратов отклонений экспериментальных и расчетных значений, fос т nl m - число степеней свободы,

соответствующее этой дисперсии (общее число опытов за вычетом числа коэффициентов модели).

Расчет дисперсии неадекватности

Имея в виду, что остаточная сумма квадратов откло-

нений складывается из суммы квадратов отклонений неаде-

кватности и суммы квадратов отклонений воспроизводимо-

сти:

SSос т SSн еад SSво с п

можно выделить сумму квадратов неадекватности:

12

SSнеад SSос т SSвосп

Удалено: ¶

Для определения дисперсии неадекватности рассчитыва-

ется число степеней свободы неадекватности по формуле:

fн еад fос т fвос пр nl m n( l 1) n m

Окончательно:

Sнеад2 SSнеад

fнеад

Проведя соответствующие подстановки, получим

	n
	l (yu		2
Sнеад2		yu )
	u 1			(2.15)
	n m

Критерий Фишера

Удалено: ¶

.Сопоставление дисперсий неадекватности и диспер-

сии воспроизводимости проводится по критерию Фишера:

	2			Удалено: ¶
	F	Sнеад		(2.16)
		Sвоспр2

Полученное расчетом значение сравнивается с таб-

личным, определенным для соответствующих степеней сво-

боды. Если F < Fтабл - уравнение адекватно.

Если модель адекватна, переходят к анализу ее ко-

эффициентов, в случае неадекватности модели, меняют по-

11

рядок полинома и анализ адекватности повторяют. При де-

терминированном подходе в такой ситуации меняют число коэффициентов модкли в рамках рассматриваемой структу-

ры, или меняют структуру модели.

2.22. Анализ коэффициентов полинома

Другой задачей статистической обработки является

оценка точности определения коэффициентов и

анализ значимости коэффициентов. В общем случае дисперсию коэффициентов можно определить по уравне-

нию

2	2	,	(2.17)
Sb j	Cjj Sвос п

где Cjj - диагональные элементы ковариационной матрицы

(см. уравнение 2.11).

Для конкретной структуры полинома выведены расчетные формулы, например, для однофакторной линейной зависи-

мости (y=b0+b1x) расчет дисперсии коэффициентов прово-

дится по уравнениям:

						n
	2					xu2
S2	Sвос пр			и S2	S2	u 1	,	(2.18)
	n
b1				b0	b1	n
	(xu	x	)2

u=1

12

n

xu

куда входят среднее значение факторов x u 1 и среднее n

n

xu2

значение квадратов факторов u 1 . n

Оценка ошибки определения коэффициента считается как

S S 2 1.

bj bj

Оценка значимости коэффициентов проводится по критерию Стьюдента, как отношение абсолютного значения коэффи-

циента к ошибке его определения:

t j	bj		,
	Sbj

(2.19)

Если определенное таким образом значение критерия для j-того коэффициента меньше некоего критического зна-

чения (t j tк р) , то соответствующий коэффициент незна-

чим и может быть исключен из уравнения. Значение tк р

находят по таблице в соответствии с выбранным уровнем значимости (обычно 0,05) и числом степеней свободы для

1 Величина среднеквадратичного отклонения в теоретической статистике имеет более сложный смысл, для практического использования мы можем назвать эту величинуошибкой определения коэффициента.

11

средней дисперсии воспроизводимости. После исключения

какого-либо коэффициента анализ адекватности повторяют.

2.3. Подход к обработке простой линейной зависимости.

На примере простой, но достаточно распространенной в практике линейной однофакторной зависимости вида y=b0+b1x *) рассмотрим при-

менение рассмотренной выше общей методики анализа результатов эксперимента. Для этого уравнения формулы для расчета коэффициен-

тов на основе результатов эксперимента, которые для общего случая мы записали в виде матричного уравнения (2.11), могут быть выведены не-

зависимо. Мы проведем этот вывод и на примере конкретного расчета воспользуемся полученными формулами и уравнением (2.11).

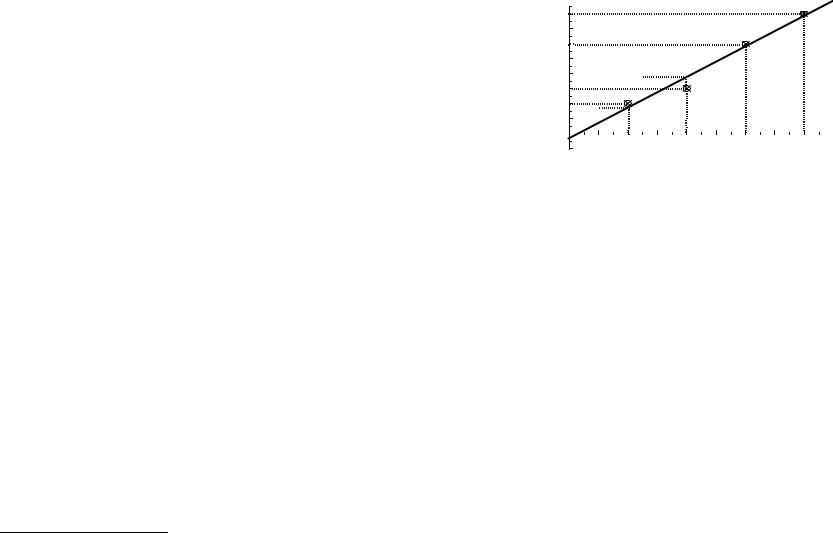
На графике (рис.2.1) изобразим зависимость y(x) в виде несколь-

ких экспериментальных точек (y1(x1), y2(x2), y3(x3), y4(x4)) и проведем че-

рез эти точки прямую так, как нам это представляется естественным.

*) Простой пример: lnk=lnk0 - E/RT

12

y

y4 8
7
y3 6
5
4				y2
y2 3
y1 2			y1
1
0										x
0,0		0,5	1,0	1,5	2,0	2,5	3,0	3,5	4,0
-1			x1		x2		x3		x4

Рис. 2.1. Описание экспериментальных результатов линейной за-

висимостью.

Проведенная таким образом прямая уже позволяет оценить зна-

чения коэффициентов уравнения (b0=-0,3 ; b1=2,2), нашей же задачей является вывод расчетных формул на основе метода наименьших квад-

ратов. В соответствии с этим методом необходимо минимизировать сум-

му квадратов отклонений экспериментальных и расчетных значений от-

кликов - результатов эксперимента (y). Запишем отдельные отклонения:

y1 y1 (b0 b1 x1 )
y	2	y	2	(b b x		2	)
				0	1
.................								,
y	u	y	u	(b b x		u	)
				0	1
...................
		yn (b0 b1 xn )
yn

11

квадрат i-того отклонения: ( yu )2 [yu (b0 b1xu )]2 и, наконец, сумму

квадратов отклонений (сравните с общими выражениями 2.2 и 2.3), кото-

рая должна быть минимизирована:

n

SS [yu (b0 b1xu )]2 min

u 1

Далее приравниваем нулю производные суммы квадратов отклонений по каждому из коэффициентов:

	dSS	0
db
	0		,
	dSS
		0
db1

берутся соответствующие производные и проводятся преобразования по аналогии с системами 2.4)-(2.5):

n			(b0	b1xu )]( 1)} 0
{ 2[yu
u 1
n
			(b0	b1xu )]( xu )} 0
{ 2[yu
u 1
n		n	n
yu b0 (b1xu ) 0
u 1		u 1	u 1
n			n		n
						2
(yu xu )			(b0 xu ) (b1xu ) 0
			u 1		u 1
u 1
	n			n
yu nb0 b1 xu 0
u 1				u 1
	n		n		n
					2	0
(yu xu ) b0 xu b1 xu
			u 1		u 1
u 1

откуда получаем расчетные формулы для определения коэффициентов:

						12
			n	n		n			n
			y u x u2 ( y u x u ) x u
b0			u 1	u 1		u 1			u 1
				n		n
					2	( x u )			2
				n xu
				u 1		u 1
			n			n		n
		n ( y u xu			) y u x u
			u 1			u 1	u 1
b1
				n		n		2
				2
			n	x u	( xu )
				u 1		u 1

Приведем пример расчета коэффициентов по экспериментальным зна-

чениям, приведенным на рисунке 2.1. Экспериментальные результаты и промежуточные расчеты сведем в таблицу.

Таблица 2.4 Расчет коэффициентов линейной однофакторной модели.

Номер	Значение			Значение									xu2	Расчетное
опыта	фактора			отклика				yuxu						значение
u	xu			yn										y
1	1			2				2					1	1,6
2	2			3				6					4	3,7
3	3			6				18					9	5,8
4	4			8				32					16	7,9
Сумма	10			19				58					30	-
Расчет коэффициентов дает:
			19 *30 58*10							570 580
	b0												0,5
				4 *30 100						120 100
			4 *58 19 *10						232 190
	b											2,1
								20
	1			4 *30 100

Как видно полученные расчетом коэффициенты отличаются от тех, что мы оценили непосредственно по графику, хотя отличие невелико.

11

Естественно, что те же результаты мы получим, используя не специфические расчетные формулы для этого случая, а непосредствен-

но общее матричное уравнение (2.11). Используем этот подход для того же примера экспериментальных данных. Расчет проводим по матричной формуле (2.11): B (XTX) 1 XTY. В основе расчета лежит матрица факторов, состоящая из четырех строк (число опытов) и двух столбцов

(формальный фактор, который всегда равен единице, и единственный в этом случае реальный фактор):

	1		1
		1
X			2
		1
			3
	1		4

Другой исходной матрицей является матрица откликов, которая имеет один столбец и число строк, равное числу опытов, т.е. четырем в данном случае:

2

Y 3

6

8

Переходим к расчету по формуле 2.11. Транспонированная матрица фак-

торов запишется без всяких затруднений:

1		1	1	1
XT	1	2	3
				4

Произведение транспонированной и исходной матрицы факторов (ин-

формационная матрица) провести вручную можно, но уже сложнее, чем транспонирование, поэтому при желании можно воспользоваться расчет-

ной программой (см. приложение).:

							12
						1	1
		1	1	1	1			4	10
X	T					1 2
		X	2	3		1	3
		1			4			10	30
						1	4

Проведя обращение этой матрицы, получаем ковариационную матрицу

(даже в этом простом случае нет смысла проводить обращение вручную,

лучше воспользоваться компьютерной программой (см. приложение)):

(XTX) 1		4	10 1		15.	0.5
						0.2
	10		30	05.

Следующий шаг - умножение ковариационной матрицы на транспониро-

ванную матрицу факторов:

	15.	05. 1		1	1	1		1	05.	0	05.
(XT X) 1 XT		02.		2	3				01.	01.	03.
05.			1			4	03.

Инаконец, рассчитываем искомый вектор коэффициентов:

2

	1	05.	0	05.		3	05.
B (XTX) 1 XTY		01.	01.	03.				21.
03.						6

8

Понятно, что мы получили те же значения коэффициентов, что при рас-

чете по специальным для этого случая формулам. Для обработки более сложных зависимостей следует пользоваться этой техником матричного расчета.

Теперь на этом же простом примере проведем статистическую обработку полученных результатов. Сначала займемся проверкой адек-

ватности модели и эксперимента, для чего сначала надо определить дисперсию воспроизводимости. Для определения дисперсии воспроиз-