
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
Государственное образовательное учреждение
высшего профессионального образования
«МАТИ» - РОССИЙСКИЙ ГОСУДАРСТВЕННЫЙ
ТЕХНОЛОГИЧЕСКИЙ УНИВЕРСИТЕТ
имени К.Э. ЦИОЛКОВСКОГО
Кафедра «Моделирование систем и информационные технологии»
Проверка статистических гипотез.
Гипотезы о дисперсиях
Методические указания к практическим занятиям
по дисциплине «Математическая статистика»
Составители: Егорова Ю.Б.
Мамонов И.М.
МОСКВА 2009
Проверка статистических гипотез. Гипотезы о дисперсиях: Методические указания к практическим занятиям по дисциплине «Математическая статистика»/ Ю.Б. Егорова, И.М. Мамонов. М.: МАТИ, 2009. – 16 с.
Егорова Ю.Б.,
Мамонов И.М.,
составление, 2009
МАТИ, 2009
ВВЕДЕНИЕ
Методические указания предназначены для студентов дневного отделения факультета №14 специальностей 230102, 220231 и являются учебным руководством при выполнении индивидуального задания.
ПРОВЕРКА ГИПОТЕЗЫ О СРАВНЕНИИ
ИСПРАВЛЕННОЙ ВЫБОРОЧНОЙ ДИСПЕРСИИ С
ГЕНЕРАЛЬНОЙ ДИСПЕРСИЕЙ
Пусть
генеральная совокупность исследуемой
случайной величины Х
распределена нормально: Х~N(m,σ).
Предположим, что генеральная дисперсия
D(X)=σ2
неизвестна, но можно полагать, что она
равна некоторому числу
![]() ,
например, задана по проекту.
,
например, задана по проекту.
Из
генеральной совокупности Х
сделаем выборку объемом n
(n<30).
Найдем выборочное среднее
![]() и «исправленную» выборочную дисперсию
и «исправленную» выборочную дисперсию
![]() .
.
При
заданном уровне значимости α
необходимо проверить нулевую гипотезу,
состоящую в том, что «исправленная»
выборочная дисперсия и генеральная
дисперсия различаются незначимо, т.е.
генеральная дисперсия равна значению![]() :
:
Но:
D(Х)=![]() .
.
Сравнение производится с помощью специально подобранной случайной величины – статистического критерия χ2, имеющего закон распределения Пирсона с k=n-1 степенями свободы:
![]()
Критическая область строится в зависимости от вида альтернативной (конкурирующей) гипотезы.
Первый случай.
Выдвигаем
нулевую гипотезу Но:
D(Х)=![]() .
.
Выдвигаем
альтернативную гипотезу Н1:
D(Х)≠![]() .
.
В этом случае строят двустороннюю критическую область.
Порядок проверки нулевой гипотезы:
по выборке определяем наблюдаемое значение критерия
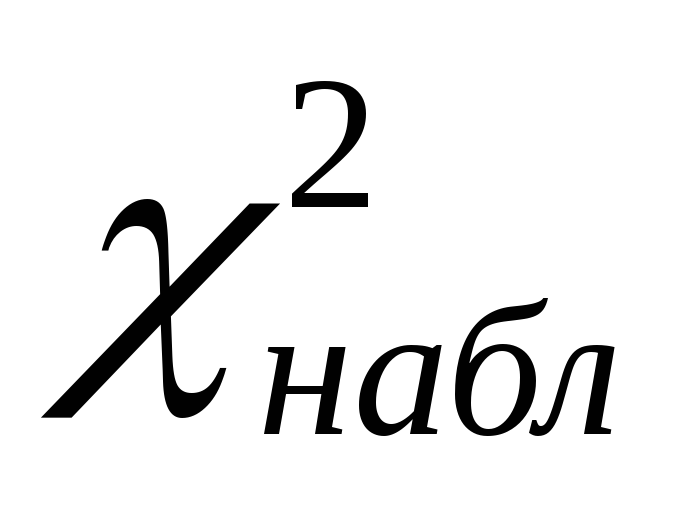 .
.по таблице критических точек распределения Пирсона (см. Приложение 1) определяем левую
 и правую
и правую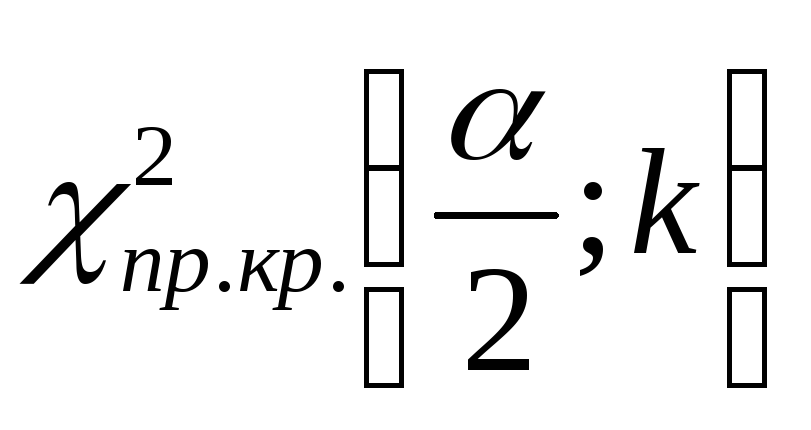 критические
точки.
критические
точки.Если
 ,
то нулевая гипотеза принимается.
,
то нулевая гипотеза принимается.
Если
![]() или
или![]() ,
то нулевая гипотеза отвергается и
принимается альтернативная.
,
то нулевая гипотеза отвергается и
принимается альтернативная.
Второй случай.
Выдвигаем
нулевую гипотезу Но:
D(Х)=![]() .
.
Выдвигаем
альтернативную гипотезу Н1:
D(Х)>![]() .
.
В этом случае строят правостороннюю критическую область.
Порядок проверки нулевой гипотезы:
по выборке определяем наблюдаемое значение критерия
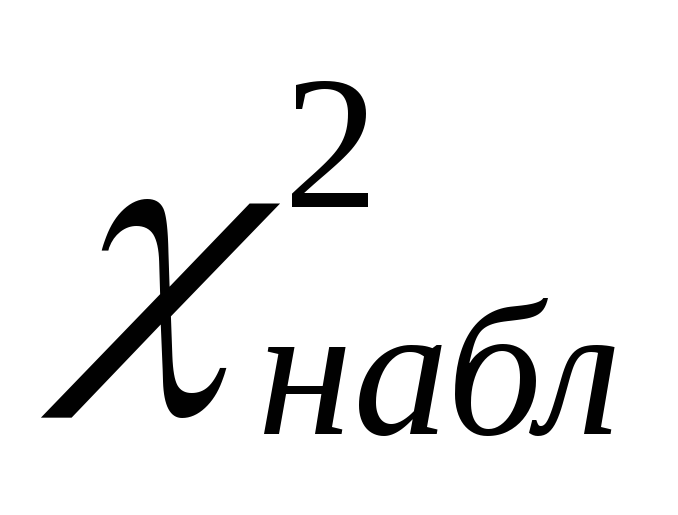 .
.по таблице критических точек распределения Пирсона (см. Приложение 1) определяем критическую точку
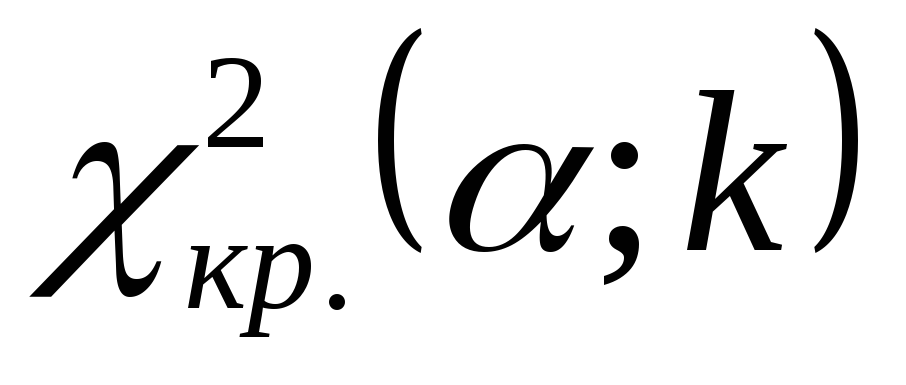 .
.Если
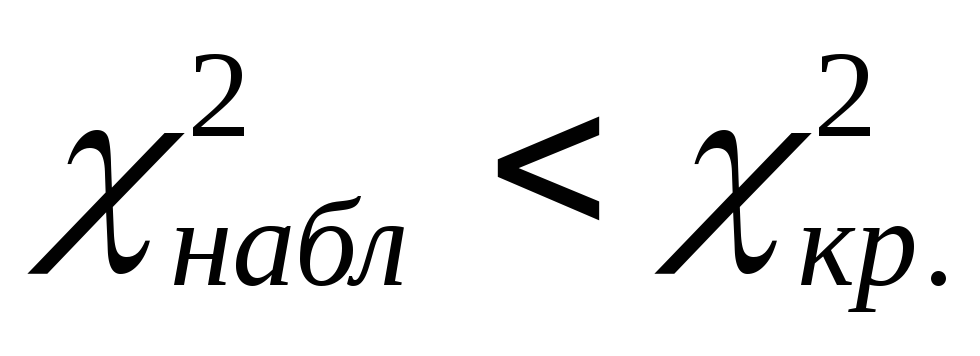 ,
то нулевая гипотеза принимается.
,
то нулевая гипотеза принимается.
Если
![]() ,
то нулевая гипотеза отвергается и
принимается альтернативная.
,
то нулевая гипотеза отвергается и
принимается альтернативная.
Третий случай.
Выдвигаем
нулевую гипотезу Но:
D(Х)=![]() .
.
Выдвигаем
альтернативную гипотезу Н1:
D(Х)<![]() .
.
В этом случае строят левостороннюю критическую область.
Порядок проверки нулевой гипотезы:
по выборке определяем наблюдаемое значение критерия
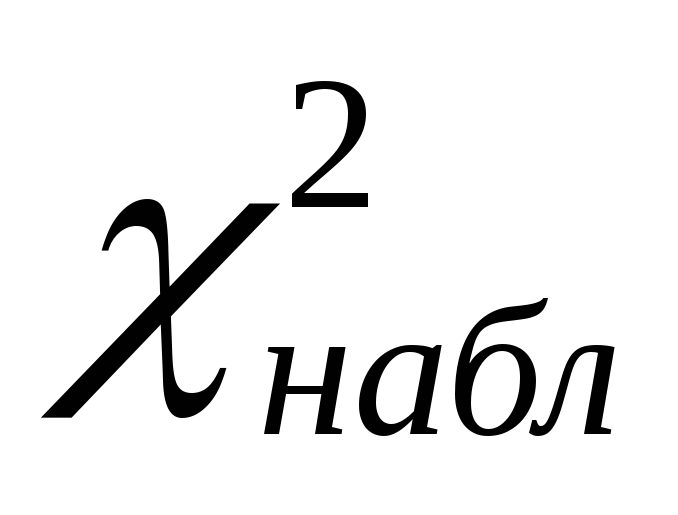 .
.по таблице критических точек распределения Пирсона (см. Приложение 1) определяем критическую точку
 .
.Если
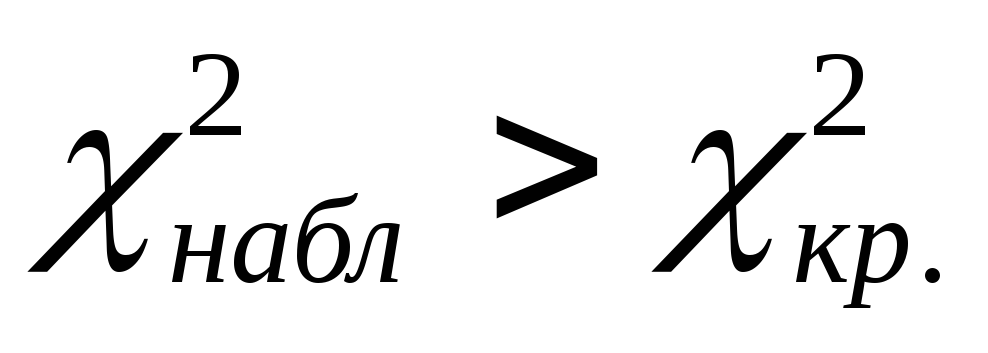 ,
то нулевая гипотеза принимается.
,
то нулевая гипотеза принимается.
Если
![]() ,
то нулевая гипотеза отвергается и
принимается альтернативная.
,
то нулевая гипотеза отвергается и
принимается альтернативная.
ПРИМЕР 1. Точность работы термопары в печи измеряется по дисперсии температуры, которая по техническим условиям не должна превышать 12 (0С)2. После измерения температуры 13 изделий была получена «исправленная» выборочная дисперсия 12,3 (0С)2. Можно ли по данным выборки при уровне значимости 0,05 считать, что точность работы термопары соответствует норме?
РЕШЕНИЕ. По
условию n=13;
D(X)=![]() =12
(0С)2;
=12
(0С)2;
![]() (0С)2;
α=0,05.
(0С)2;
α=0,05.
Выдвигаем нулевую
гипотезу Но:
D(Х)=![]() .
Относительно альтернативной гипотезы
возможны два случая: а)D(Х)≠
.
Относительно альтернативной гипотезы
возможны два случая: а)D(Х)≠![]() .;
б)Н1:
D(Х)>
.;
б)Н1:
D(Х)>![]() .
(так как
.
(так как
![]() ).
Рассмотрим эти случаи.
).
Рассмотрим эти случаи.
а) Первый случай.
Но: D(Х)=12 (0С)2.
Н1: D(Х)≠12 (0С)2.
В этом случае строят двустороннюю критическую область.
Порядок проверки нулевой гипотезы:
по выборке определяем наблюдаемое значение критерия
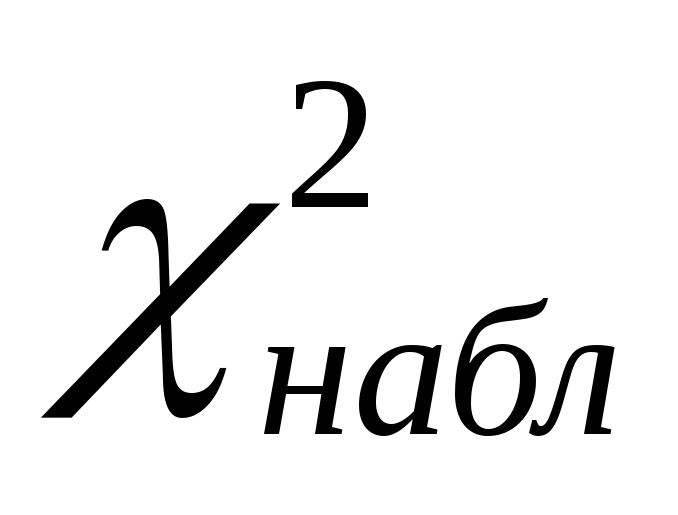 :
:
![]()
по таблице критических точек распределения Пирсона (см. Приложение 1) определяем левую и правую критические точки:
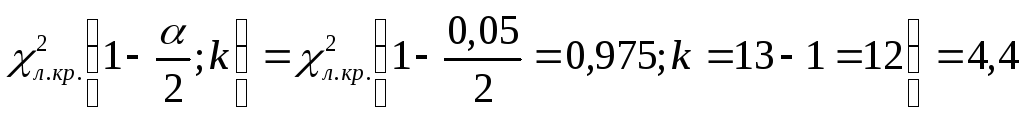 ;
;
![]()
Так как
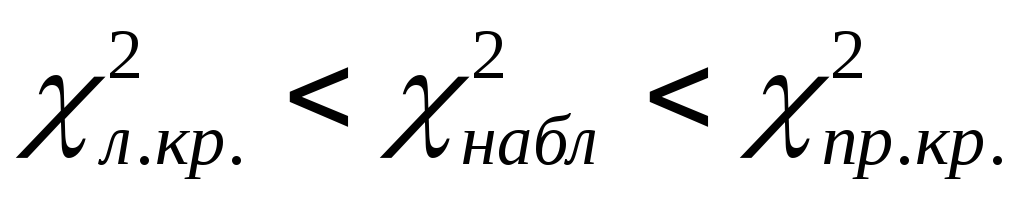 ,
то нулевая гипотеза принимается.
,
то нулевая гипотеза принимается.
б) Второй случай.
Но: D(Х)=12 (0С)2.
Н1: D(Х)>12 (0С)2.
В этом случае строят правостороннюю критическую область.
Порядок проверки нулевой гипотезы:
по выборке определяем наблюдаемое значение критерия
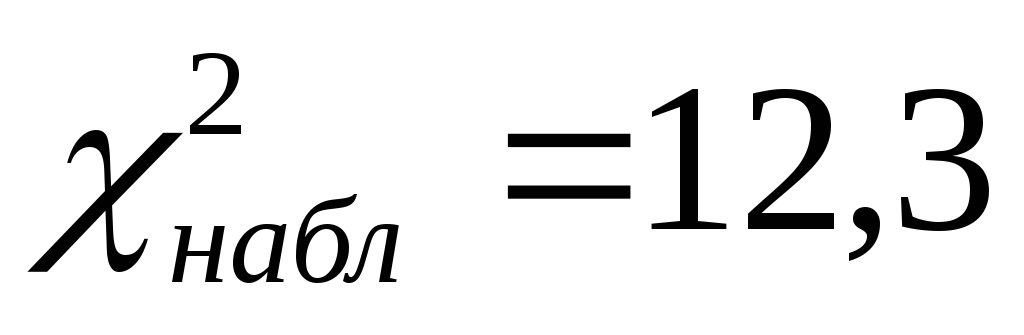 .
.по таблице критических точек распределения Пирсона (см. Приложение 1) определяем критическую точку
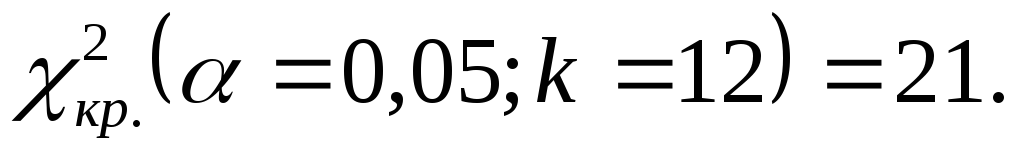
Так как
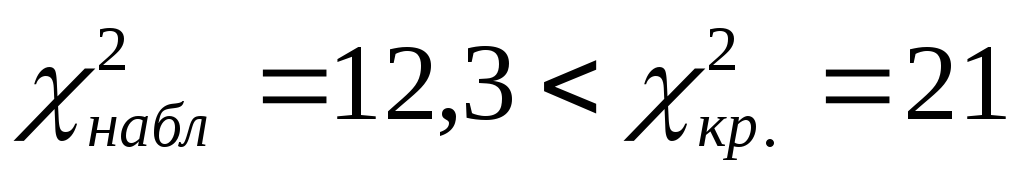 ,
то нулевая гипотеза принимается.
,
то нулевая гипотеза принимается.
Таким образом, с вероятностью 0,95 можно утверждать, что «исправленная» выборочная дисперсия и генеральная дисперсия различаются незначимо и, следовательно, точность работы термопары в печи соответствует норме.
