Проверка гипотезы о сравнении двух дисперсий
Пусть генеральные совокупности исследуемых случайных величин Х и Y распределены нормально: Х~N(mх,σх) и Y~N(my,σy). Генеральные дисперсии D(X) и D(Y) неизвестны.
Из
генеральных совокупностей Х
и Y
сделаем выборки объемами n1
и n2.
Найдем соответственно выборочные
средние
и
и «исправленные» дисперсии
и
.
При заданном уровне значимости α необходимо проверить нулевую гипотезу, состоящую в том, что «исправленные» выборочные дисперсии различаются незначимо, т.е. генеральные дисперсии равны между собой:
Но: D(Х)= D(Y).
Сравнение производится с помощью специально подобранной случайной величины – статистического критерия F, имеющего закон распределения Фишера-Снедекора со степенями свободы k1=n1-1 и k2=n2-1:
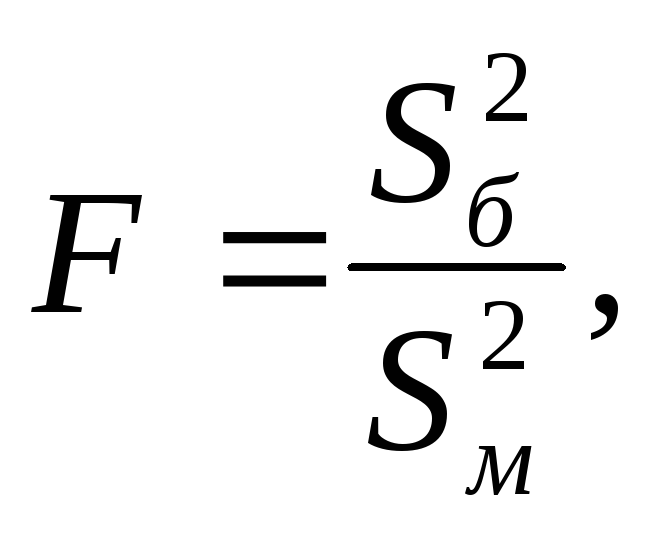
где
и
– большая и меньшая дисперсия
соответственно;k1
– число степеней свободы большей
дисперсии; k2
– число степеней свободы меньшей
дисперсии.
Критическая область строится в зависимости от вида альтернативной (конкурирующей) гипотезы.
Первый случай.
Выдвигаем нулевую гипотезу Но: D(Х)= D(Y).
Выдвигаем альтернативную гипотезу Н1: D(Х)≠ D(Y).
В этом случае строят двустороннюю критическую область.
Порядок проверки нулевой гипотезы:
по выборке определяем наблюдаемое значение критерия
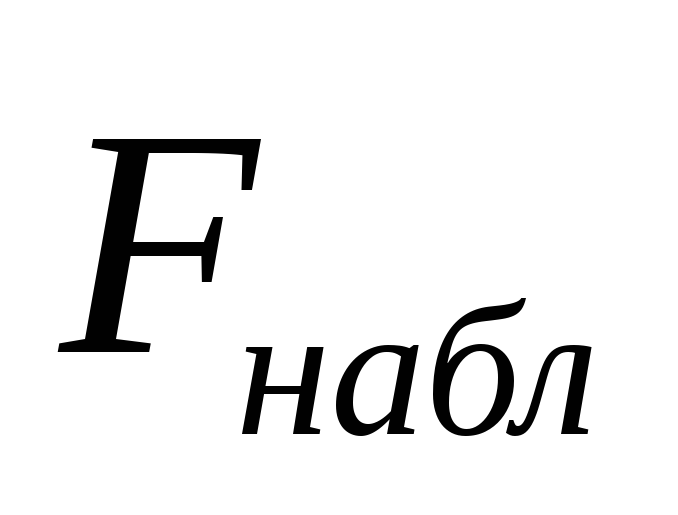.по таблице критических точек распределения Фишера-Снедекора (см. Приложение 2) определяем критическую точку
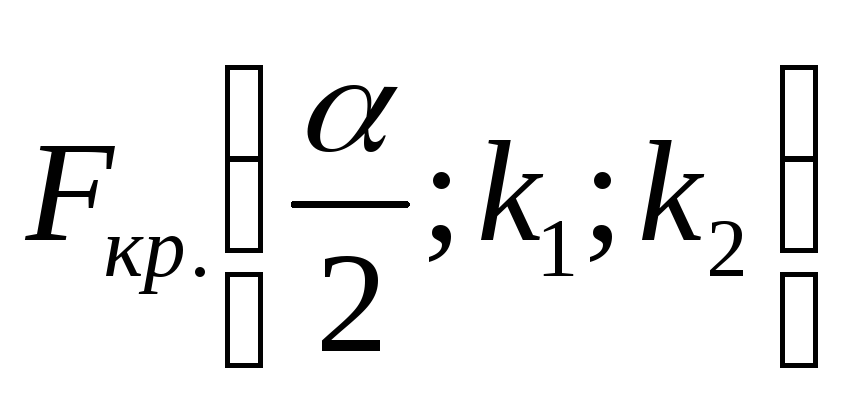в зависимости от уровня значимостиα
и числа степеней свободы k1=n1-1
и k2=n2-1.Если
,
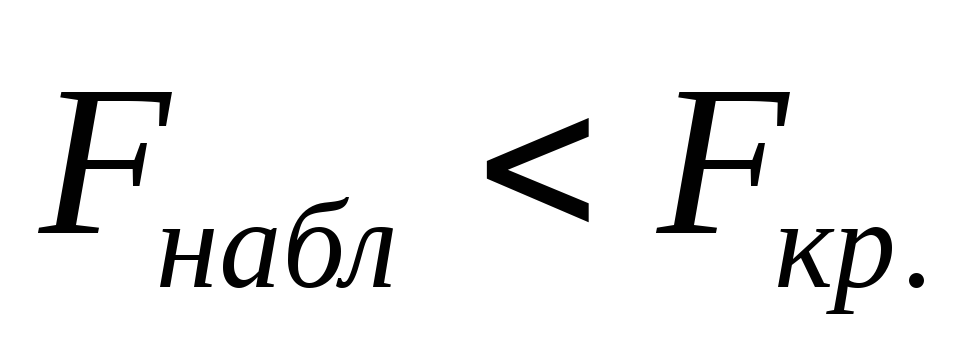то нулевая гипотеза принимается.
Если
,
то нулевая гипотеза отвергается и
принимается альтернативная.
Второй случай.
Выдвигаем нулевую гипотезу Но: D(Х)= D(Y).
Выдвигаем альтернативную гипотезу Н1: D(Х)> D(Y).
В этом случае строят правостороннюю критическую область.
Порядок проверки нулевой гипотезы:
по выборке определяем наблюдаемое значение критерия
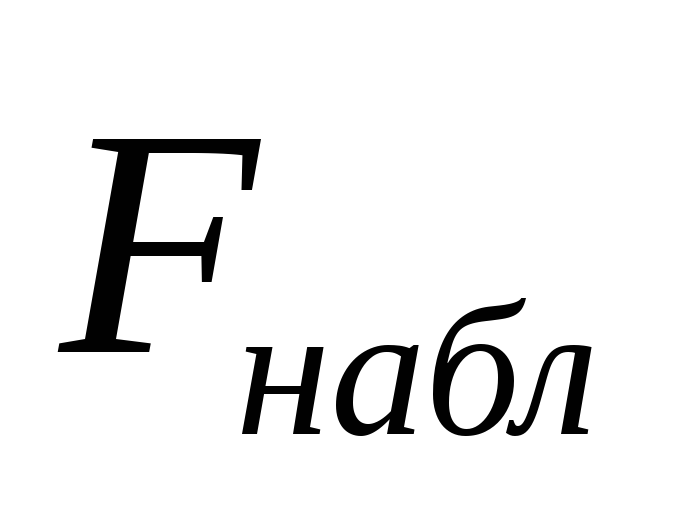.по таблице критических точек распределения Фишера-Снедекора (см. Приложение 2) определяем критическую точку
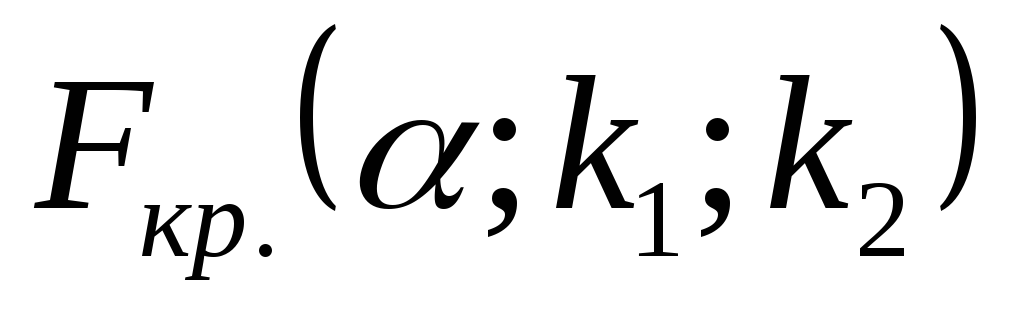в зависимости от уровня значимостиα
и числа степеней свободы k1=n1-1
и k2=n2-1.Если
,
то нулевая гипотеза принимается.
Если
,
то нулевая гипотеза отвергается и
принимается альтернативная.
ПРИМЕР 2. Технологи механосборочного цеха считают, что применение нового резца позволит сократить время обработки детали. Пять деталей были изготовлены старым резцом: среднее время обработки одной детали составило 3,3 мин с «исправленной» дисперсией – 0,25 мин2. Шесть деталей были изготовлены новым резцом: среднее время обработки одной детали составило 2,48 мин с «исправленной» дисперсией – 0,108 мин2. При уровне значимости 0,05 проверьте, значимо ли различаются «исправленные» выборочные дисперсии.
РЕШЕНИЕ.
По условию
n1=5;
мин;
мин.2;
n2=6;
мин;
мин2,
α=0,05.
Выдвигаем нулевую
гипотезу Но:
D(Х)=
D(Y).
Относительно альтернативной гипотезы
возможны два случая: а) D(Х)≠
D(Y).;
б) Н1:
D(Х)>
D(Y).
(так как
).
Рассмотрим эти случаи.
а) Первый случай.
Выдвигаем нулевую гипотезу Но: D(Х)= D(Y).
Выдвигаем альтернативную гипотезу Н1: D(Х)≠ D(Y).
В этом случае строят двустороннюю критическую область.
Порядок проверки нулевой гипотезы:
по выборке определяем наблюдаемое значение критерия
:
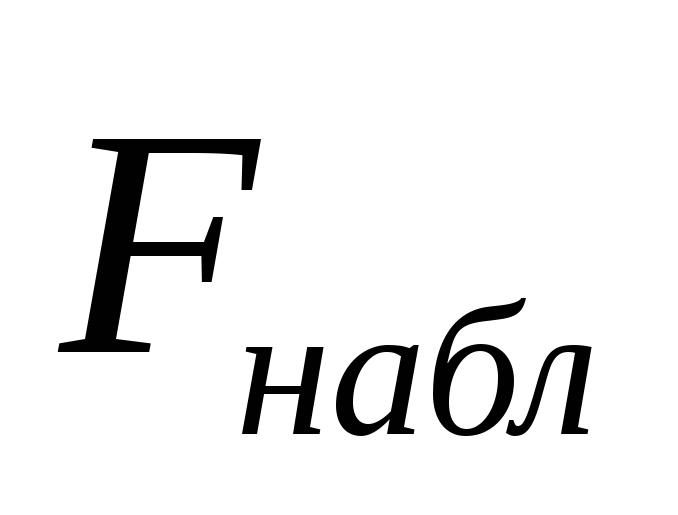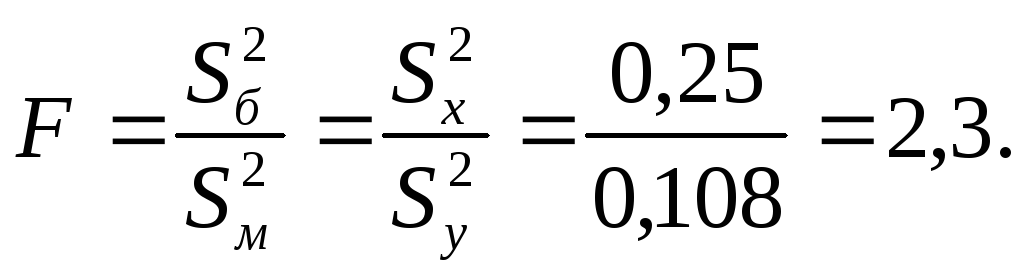
по таблице критических точек распределения Фишера-Снедекора (см. Приложение 2) определяем критическую точку
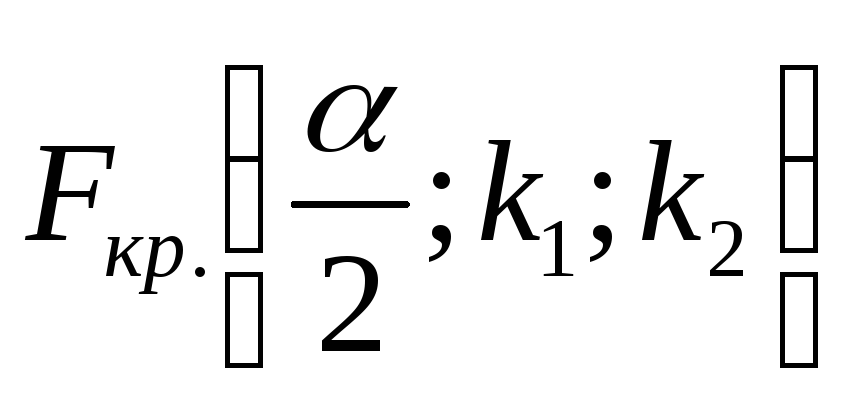в зависимости от уровня значимостиα=0,05
и числа степеней свободы k1=n1-1=5-1=4
и k2=n2-1=6-1=5:
Если
,
то нулевая гипотеза принимается.
б) Второй случай.
Выдвигаем нулевую гипотезу Но: D(Х)= D(Y).
Выдвигаем альтернативную гипотезу Н1: D(Х)> D(Y).
В этом случае строят правостороннюю критическую область.
Порядок проверки нулевой гипотезы:
по выборке определяем наблюдаемое значение критерия
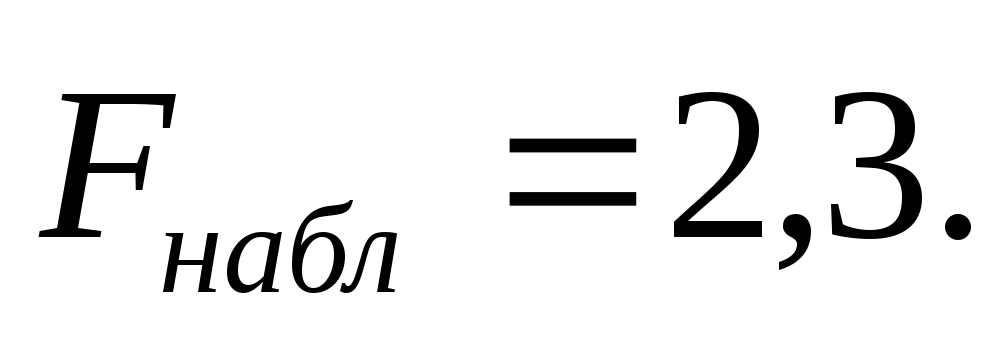
по таблице критических точек распределения Фишера-Снедекора (см. Приложение 2) определяем критическую точку
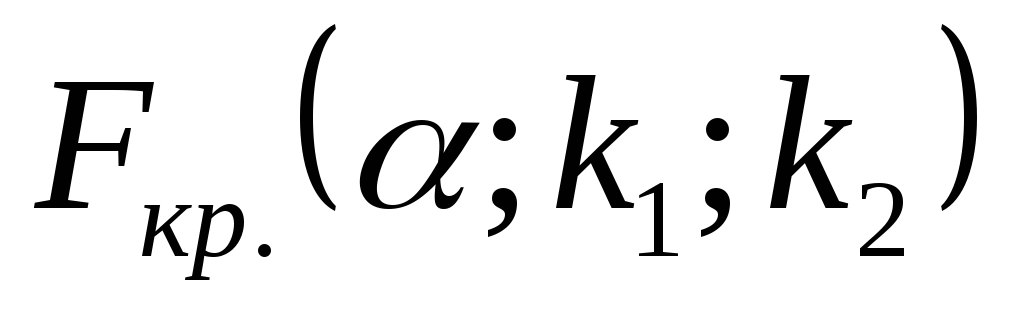в зависимости от уровня значимостиα=0,02
и числа степеней свободы k1=n1-1=5-1=4
и k2=n2-1=6-1=5:
Если
,
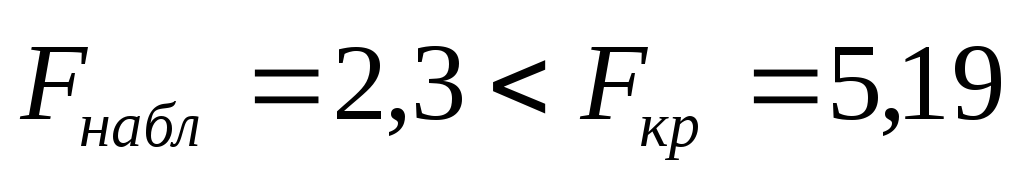то нулевая гипотеза принимается.
Таким образом, с вероятностью 0,95 можно утверждать, что «исправленные» выборочные дисперсии различаются незначимо и, следовательно, можно считать, что генеральные дисперсии равны.