2. Построение нормальной кривой по опытным данным

Нормальной кривой называется график плотности распределения вероятностей нормальной случайной величины. ^{Теоретическая плотность распределения вероятностей (дифференциальная функция распределения) имеет вид:}

^{где m и  - параметры нормального распределения: m=М(Х) - математическое ожидание случайной величины Х, =(Х) - среднее квадратическое отклонение.}

^{Эмпирическая плотность распределения вероятностей имеет вид:}

где и * – статистические оценки m и , определенные по выборке.

^{Для построения теоретической нормальной кривой можно использовать несколько методов. Рассмотрим приблизительный способ построения с использованием результатов расчетов, сделанных в примере 1.}

^{Значения эмпирической плотности распределения вероятностей можно приблизительно определить по соотношению:}

^{где xi – ширина интервала, n – объем выборки.}

^{При построении теоретической нормальной кривой необходимо учитывать следующие свойства нормального распределения:}

1. ^{приблизительно все значения х лежат в «3»-интервале:}

2. ^{нормальная кривая симметрична относительно прямой}

3. ^{максимум нормальной кривой находится в точке}

^{Гистограмму, полигон частот и нормальную кривую целесообразно совместить на одном графике.}

^{ПРИМЕР 2. Построить гистограмму, полигон эмпирических частот и нормальную кривую по данным примера 1.}

^{РЕШЕНИЕ.}

^{1) Гистограмма – это фигура из столбцов, основание которых равно ширине интервала xi, а высота – частоте ni . Если соединить середины интервалов отрезками прямых, получим полигон эмпирических частот в координатах (xi, ni). Значения интервалов и эмпирических частот приведены в табл.4.}

^{2) Определяем значения f*(x). В примере 1 ширина интервала xi=6%, а объем выборки n=100. Тогда получим:}

^{Значения f*(x) приведены в столбце 7 табл. 4.}

^{3) Определяем «3»-интервал:}

^{4) нормальная кривая симметрична относительно прямой}

^{5) максимум нормальной кривой находится в точке}

^{На рис. 1 построены гистограмма, полигон эмпирических частот и нормальная кривая. Сравнение графиков наглядно показывает, что теоретическая кривая удовлетворительно отражает опытные данные. Близость нормальной кривой к эмпирическим частотам подтверждает правильность допущения о том, что исследуемая случайная величинаХ распределена нормально.}

3. Проверка гипотезы о законе распределения по критерию колмогорова

Пусть эмпирическое распределение задано в виде таблицы, в которой перечислены варианты x_i и значения эмпирической функции распределения F*(x) (табл.5).

Таблица 5

Значения эмпирической функции распределения

xi	x1	x2	…	xn
F*(x)	F*(x1)	F*(x2)		F*(xn)

Для каждого значения x_i определим теоретические значения функции распределения F(x). При уровне значимости  необходимо проверить, насколько сильно эмпирическая функция распределения F*(x) отличается от теоретической F(x).

В этом случае в качестве критерия для проверки статистической гипотезы о неизвестном законе распределения генеральной совокупности используется случайная величина D, которая называется критерием согласия Колмогорова:

где D – максимальное значение абсолютной величины разности между эмпирической и теоретической функциями распределения.

Порядок проверки нулевой гипотезы:

1. по выборке определяем D и вычисляем наблюдаемое значение величины .

2. по таблице распределения Колмогорова (см. Приложение 2) определяем критическое значения критерия 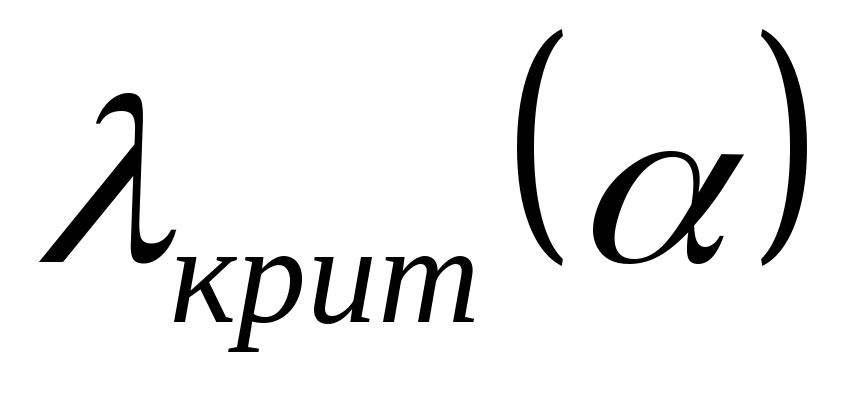в зависимости от уровня значимостиα.

3. Если , то нулевая гипотеза принимается.

Если , то нулевая гипотеза отвергается.

ПРИМЕР 3. По данным примера 1 с помощью критерия Колмогорова при уровне значимости  =0,05 необходимо проверить нулевую гипотезу о том, что случайная величина Х имеет нормальный закон распределения.

РЕШЕНИЕ. Выдвигаем нулевую гипотезу Н_о: случайная величина Х имеет нормальный закон распределения с параметрами N(119,2; 9,35). Выдвигаем альтернативную гипотезу Н₁: случайная величина Х не имеет нормальный закон распределения с параметрами N(119,2; 9,35).

Сначала определяем значения относительных частот W_i, накопленных частот n_нак, накопленных частостей W_нак (табл.5) и значения эмпирической функции распределения F*(x) (табл.6).

Таблица 6

Группированный статистический ряд, статистическое распределение частот, относительных частот, накопленных частот и частостей

№ интервала	1	2	3	4	5	6	7	8
xi, %	94-100	100-106	106-112	112-118	118-124	124-130	130-136	136-142
ni	3	7	11	20	28	19	10	2
nнак	3	10	21	41	69	88	98	100
Wi	0,03	0,07	0,11	0,20	0,28	0,19	0,10	0,02
Wнак	0,03	0,10	0,21	0,41	0,69	0,88	0,98	1,00

Для непрерывных случайных величин значения эмпирической функции распределения F*(x) можно найти только на концах интервала (табл. 6), так как неизвестно, сколько значений случайной величины, принадлежащих этому интервалу, меньше х.

Для определения теоретической функции распределения используем функцию Лапласа (см. Приложение 3):

Например:

Результаты вычислений обобщим в табл.7 и на рис. 2, откуда следует, что:

Таблица 7