- 111-

5. Численное интегрирование обыкновеных дифференциальных уравнений

Наиболее универсальными методами численного решения обыкновенных дифференциальных уравнений являются разностные методы. Они основаны на замене производных в дифференциальном уравнении разностными отношениями. В результате исходное дифференциальное уравнение сводится к системе алгебраических уравнений, которые называются разностными. Решение этой системы дает приближенное решение исходной задачи.

1. Разностная аппроксимация производных.

   1. Сеточные функции.

Пусть на отрезке задан набор точек

.

Будем называть его сеткой. Чтобы не усложнять изложения, условимся считать сетку равномерной:

, .

Пусть каждой точке сетки сопоставлено по определенному закону число. Совокупность этих чисел назовем сеточной функцией. Сеточные функции, определенные на сетке , образуют-мерное линейное пространство.

Чтобы иметь возможность сравнивать сеточные функции между собой, говорить об их близости, нужно ввести в этом пространстве норму. В этой главе мы будем пользоваться нормой , которая определяется следующим образом:

.

Это определение законно, поскольку удовлетворяет трем аксиомам нормы:

1. Норма неотрицательна

,

причем равенство нулю имеет место только для нулевого элемента.

2. Модуль числового множителя можно вынести за знак нормы

.

3. Неравенство треугольника

.

Справедливость последнего утверждения вытекает из свойства максимума:

.

2. Разностные аппроксимации первой производной.

Для сеточных функций нельзя ввести обычное понятие производной, включающее операцию предельного перехода при . Вместо производной здесь вводятся разностные отношения:

,;

,;

,.

Отношение называют правой разностной производной, отношение – левой разностной производной и отношение – центральной разностной производной.

Чтобы установить связь разностных отношений – с обычной производной, предположим, что на отрезке определена дифференцируемая функция, значения которой в точках сетки равны значениям рассматриваемой сеточной функции:. Вычислим первую производную функциив точкахи сопоставим с разностными отношениями – :

,;

,;

,.

Эти величины представляют собой погрешности аппроксимации производной с помощью разностных отношений – в точке .

Предположим, что функция дважды непрерывно дифференцируема на отрезкеи запишем для нее формулу Тейлора с остаточным членом в форме Лагранжа

,

где какое-то неизвестное нам число между нулем и единицей. Подставляя разложение в формулу , получим

.

Аналогичное представление можно получить для величины

.

Формулы и не позволяют вычислить соответствующие погрешности, но дают возможность их оценить. Функция , по предположению, непрерывна на отрезке, и, следовательно, ограничена:

, .

В результате получаем

,.

Оценки являются равномерными, поскольку не зависят от индекса . Таким образом, левое и правое разностное отношение аппроксимируют производнуюс первым порядком точности относительно .

Для оценки предположим, что функциятри раза непрерывно дифференцируема на отрезкеи продолжим разложение еще на один член

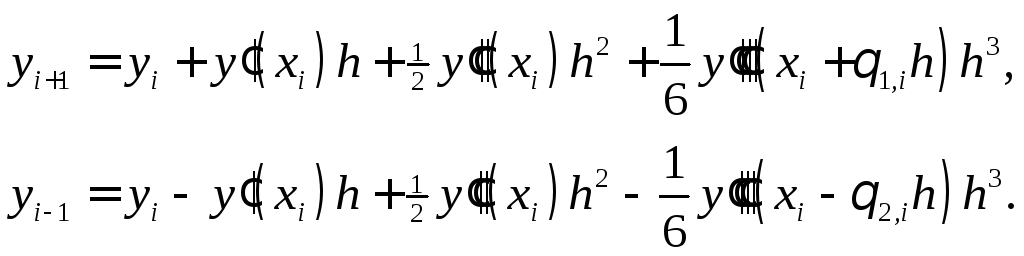
Подставляя разложения в формулу , будем иметь

.

По предположению функция непрерывна и, следовательно, ограничена на отрезке:

, .

В результате из равенства получим оценку

.

Оценка , как и раньше , не зависит от индекса , она является равномерной. Таким образом, центральная разностная производная дает более хороший результат: она аппроксимирует производнуюсо вторым порядком точности относительно для функций, трижды непрерывно дифференцируемых на отрезке.

Задача 1.

Рассмотреть функцию на сетке

,,.

Вычислить в точке правую, левую и центральную разностные производные, найти погрешности аппроксимации производной , сравнить их с априорными оценками по формулам и .

В данном случае

,

;

,

;

,

.

Перейдем к априорной оценке погрешности. Вторая и третья производные рассматриваемой функции имеют вид

,.

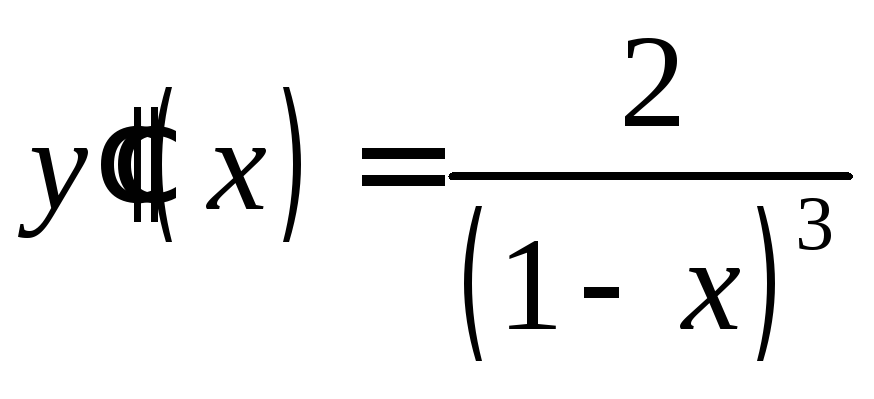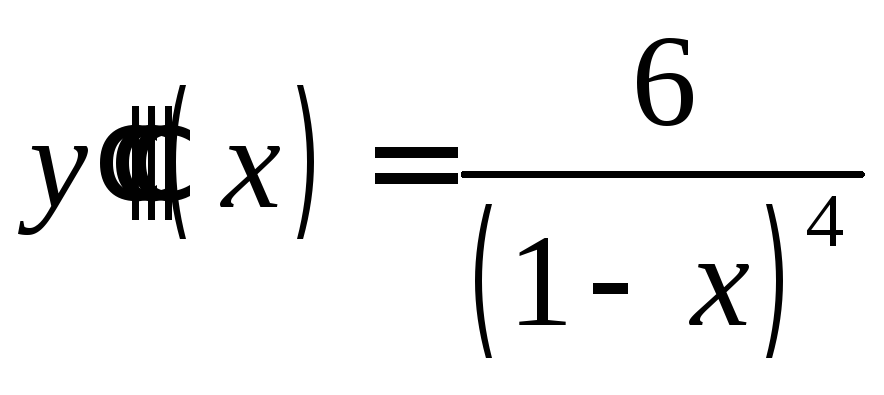Для них на отрезке справедливы оценки

,.

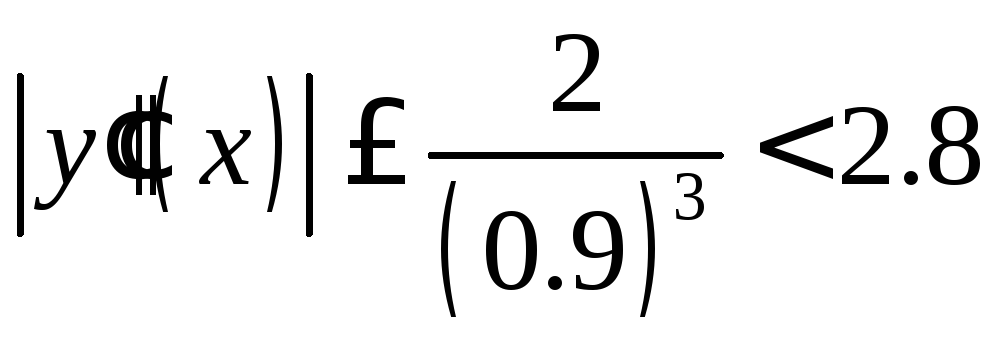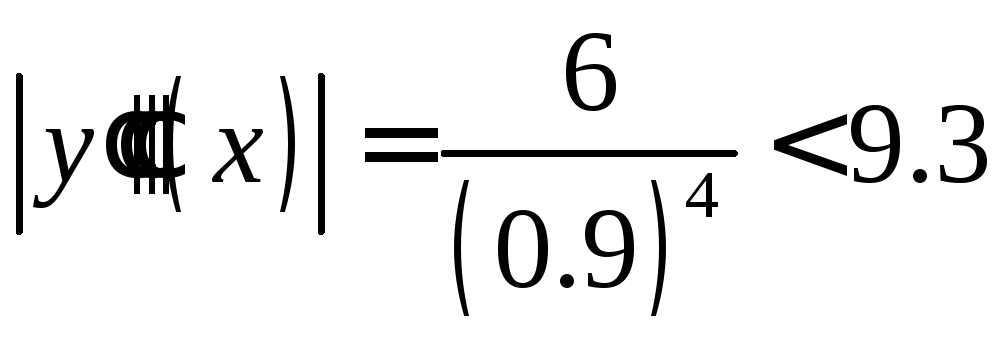Так что неравенства и запишутся следующим образом

, , .

Они выполняются.