Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Восточноукраинский национальный университет им. В. Даля

Предмет:

Дискретная математика

Файл:

Дискретная математика - Лекции 2.doc

Скачиваний:

161

Добавлен:

25.03.2015

Размер:

1.5 Mб

Скачать

☆

<<< < Предыдущая 12 / 32 3 > Следующая >>>

Лекция № 10. Рекуррентные уравнения

Введение

Линейным рекуррентным уравнением с постоянными коэффициентами называется уравнение вида

. (10.1)

Это уравнение справедливо для всех неотрицательных целых чисел n. Коэффициенты – это фиксированные числа, причём , а – заданная функция n. Если зафиксировать значения и рассматривать их как начальные условия, то шаг за шагом можно однозначно определить значения, и таким образом определить всю последовательность.

Такой алгоритм удобно использовать при численном решении рекуррентного уравнения на компьютере. Однако существуют и аналитические способы решения этих уравнений. Один из таких способов использует так называемые производящие функции. Впервые метод производящих функций был применен французским математиком Лапласом (1749-1827) для решения некоторых проблем теории вероятностей.

Производящая функция

Степенной ряд , коэффициентами которого являются элементы последовательности, называется производящей функцией. Последовательность чисел однозначно определяет производящую функцию, но обратное утверждение верно не всегда. Если указанный степенной ряд сходится, то коэффициентыопределяются поF(z) однозначно. Производящая функция отличается от z-преобразования только тем, что степени (при разложении этой функции в степенной ряд) положительны, в то время как у z-преобразования – они отрицательны. Простой заменой переменной можно преобразовать производящую функцию в z-преобразование. Поэтому для производящих функций справедливы все теоремы дискретного преобразования Лапласа.

Пусть – производящая функция последовательности чисел, аa и b – произвольные фиксированные числа.

Поскольку , то последовательностиотвечает производящая функция. Это соответствует свойству линейности преобразования Лапласа. Далее, если взять произведение производящих функций

то последовательность чисел может быть получена из последовательностейис помощью соотношения

Последняя формула следует из теоремы о свертке двух решетчатых функций.

Пример 10.1. Найдем производящие функции последовательностей чисел {1} и {n}.

Решение: Последовательности {1} соответствует ряд:

Для доказательства необходимо левую и правую часть умножить на .

Последовательности чисел {n} соответствует ряд

Поскольку выражение в скобках в правой части равенства получается дифференцированием ряда , то оно равно производной от функции 1/(1 – z). Следовательно, правая часть равна

Следующая задача показывает, что производящие функции могут быть полезными при решении линейных рекуррентных уравнений.

Пример 10.2. Решить уравнение (уравнение Фибоначчи) с начальными условиями.

Решение: Обозначим через F(z) производящую функцию последовательности чисел . Умножая обе части рекуррентного уравнения на , получим

, n = 0, 1, 2 …

Складывая эти равенства для всех n от 0 до ∞, имеем:

Заметим, что первая сумма в левой части равенства равна разности функции F(z) и первых двух членов её разложения , вторая сумма равна разностиF(z) и первого члена , а третья сумма равнаF(z). Поэтому можем записать

[F(z) – (1 + z)] – z [F(z) – 1] – z² F(z) = 0.

Отсюда находим

где ; . В результате получим

Таким образом:

Члены последовательности, полученной в этой задаче, известны как числа Фибоначчи.

Решение однородного рекуррентного уравнения

Однородное рекуррентное уравнение получается при  (n) = 0. Метод решения является обобщением решения предыдущего примера. Вначале производящая функция находится как рациональная функция, которая далее представляется в виде суммы частичных дробей и разлагается в степенной ряд. Предположим, что последовательность чисел удовлетворяет следующему однородному линейному рекуррентному уравнению

где – заданные числа и .

Для задания начальных условий фиксируем значения . Обозначим через F(z) производящую функцию последовательности

По заданным постоянным коэффициентам уравнения построим многочлен

Этот многочлен можно рассматривать как производящую функцию последовательности: . Коэффициент при иr  0 в произведении производящих функций , определяется соотношением

Он равен нулю, поскольку рекуррентное уравнение однородное. Это означает, что многочлен

имеет степень самое большее (r–1), и, следовательно, степень числителя рациональной функции F(z) = C(z) / K(z) меньше степени знаменателя.

Характеристическим многочленом линейного однородного рекуррентного уравнения называется многочлен:

имеющий степень “r”; корни этого многочлена называются характеристическими. Если различные характеристические корни (среди которых могут быть мнимые) обозначить через , а ихкратности обозначить через , то можно записать следующие равенства:

Характеристический многочлен и многочленK(z) связаны между собой соотношениями

Отсюда следует, что

Используя это, можно записать

где – неопределённый коэффициент.

Каждая дробь этой суммы имеет вид , поэтому её можно разложить в степенной ряд следующего вида:

Коэффициент при в этом ряде равен

Если заметить, что биномиальный коэффициент

входящий в последнее равенство, является многочленом степени по, то легко проверить, что

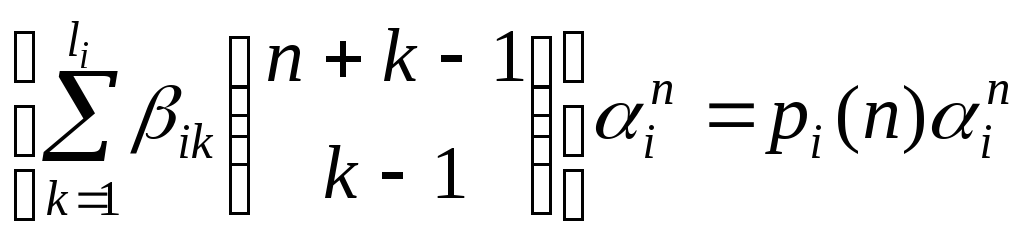где – многочлен отстепени самое большее. Следовательно

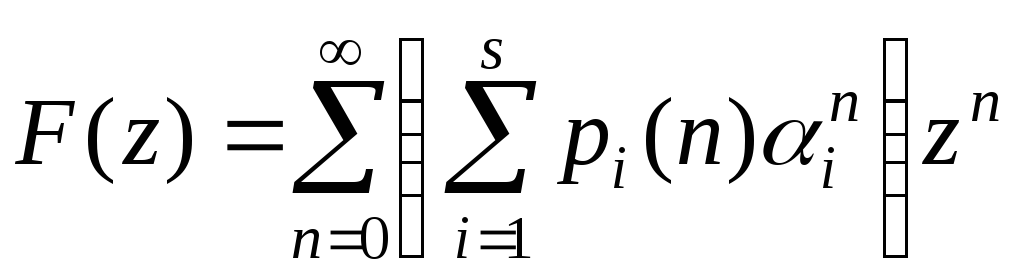
и – является общим решением однородного линейного рекуррентного уравнения.

Пример 10.3. С помощью общего метода найти общий член последовательности чисел Фибоначчи.

Решение: Уравнение имеет характеристический многочлен , где ; . В этом случае и и, следовательно, и – многочлены степени 0 от n, т.е. постоянные. Поэтому , где и – неопределённые постоянные. Так как , то, подставляяn = 0, 1, получаем ;. Решая эти уравнения, находим

; .

Отсюда следует: .

Решение этого упражнения показывает, что если все характеристические корни являются простыми, то общее решение однородного уравнения имеет вид: , где, , …, – это «r» неопределённых постоянных. Для определения этих постоянных используются r начальных условий, а именно значения . Еслиявляется корнем кратности, топредставляет собой многочлен степени:

где –неопределённых постоянных. Начальные условия однозначно определяют все «r» неопределённых постоянных.

Пример 10.4. Найти решение уравнения c начальными условиями ,.

Решение: Так как характеристический многочлен имеет кореньz = 2 кратности 2, то . С помощью начальных условий находим:

; ;.

Таким образом, решение рассматриваемого уравнения:

Метод решения неоднородного рекуррентного уравнения

Рассмотрим неоднородное линейное рекуррентное уравнение

n= 0, 1, 2, …, коэффициенты– это заданные постоянные, причём, а– заданная функцияn. Для задания начальных условий фиксируем значения.

Предположим, что одно решение уравнения найдено. Назовём это решение частным и обозначим через . Положим

Тогда: .

Так как второй член в левой части последнего равенства равен правой части, то

Это означает, что является решением однородного линейного рекуррентного уравнения, соответствующего= 0.

Таким образом, если найдено частное решение, то можно найти общее решение однородного рекуррентного уравнения. После чего по начальным условиям можно определить неопределённые коэффициенты. Для некоторых функций частное решение можно найти достаточно просто. Так, в случае если, где– константа, то частным решением является

, (10.2)

где – характеристический многочлен.

Доказательство. Подставляя, гдес– постоянная, в неоднородное рекуррентное уравнение, получаем. Таким образом:. Отсюда следует формула (10.2).

Пример 10.5.Найти решение уравнения с начальными условиями.

Решение:Данное уравнение имеет характеристический многочлен. Если бы правая часть уравнения была равна, то частным решением было бы. Длясоответствующее частное решение. Общее решение равно:

По начальным условиям находим:

, ,,,

Если является многочленом отnстепениk

и единица не является характеристическим корнем рекуррентного уравнения, т.е. , то частное решение следует искать в виде:

Подставляя этот многочлен в неоднородное рекуррентное уравнение, получим:

Так как , то,сравнивая коэффициенты при высших степенях в левой и правой частях последнего равенства, можно определить значениеи далее последовательно коэффициенты.