
Лекция № 11. Дискретное операционное исчисление
Дискретное преобразование Лапласа
Дискретное
преобразование Лапласа применяют к так
называемым решетчатым
функциям.
Решетчатой функцией
![]() называется функция, определенная только
для целых значений аргумента
называется функция, определенная только
для целых значений аргумента![]() .
(она тождественно равна нулю при
отрицательных значениях аргумента).
.
(она тождественно равна нулю при
отрицательных значениях аргумента).
Функция
![]() непрерывного аргумента
непрерывного аргумента![]() ,
определенная для всех
,
определенная для всех![]() ,
называетсяпорождающей
функцией
для решетчатой функции
,
называетсяпорождающей
функцией
для решетчатой функции
![]() .
.
а б
Рис. 11.1. Порождающая функция (а) и решетчатая функция (б)
Изображением
решетчатой функции
![]() является функция
является функция![]() ,
удовлетворяющая соотношению
,
удовлетворяющая соотношению
![]() , (11.1)
, (11.1)
где
![]() – параметр преобразования.
– параметр преобразования.
В операторной форме это соотношение записывается следующим образом:
![]() .
.
Преобразование решетчатых функций в соответствии с данным соотношением называется дискретным преобразованием Лапласа.
Всякая
функция
![]() ,
для которой существует обычное
преобразование Лапласа, порождает
решетчатую функцию
,
для которой существует обычное
преобразование Лапласа, порождает
решетчатую функцию
![]() ,
для которой, в свою очередь, определено
дискретное преобразование Лапласа.
Свойства дискретного преобразования
Лапласа решетчатой функции, в основном,
такие же, как и для обычного преобразования
Лапласа, однако здесь во всех случаях
интегралы заменяются бесконечными
суммами.
,
для которой, в свою очередь, определено
дискретное преобразование Лапласа.
Свойства дискретного преобразования
Лапласа решетчатой функции, в основном,
такие же, как и для обычного преобразования
Лапласа, однако здесь во всех случаях
интегралы заменяются бесконечными
суммами.
Предположим,
что задана последовательность чисел
![]() .
Тогда решетчатую
функцию можно представить в виде суммы
последовательностей импульсных
.
Тогда решетчатую
функцию можно представить в виде суммы
последовательностей импульсных
![]() -функцийДирака.
-функцийДирака.
![]() .
.
![]() -функция
– это специальная (обобщенная)
функция, обладающая следующими свойствами.
-функция
– это специальная (обобщенная)
функция, обладающая следующими свойствами.
![]()
![]() ,
,![]() .
.
Дискретное
преобразование Лапласа последовательности
![]() – это обычное преобразование Лапласа
импульсной функции
– это обычное преобразование Лапласа
импульсной функции![]() :
:
![]() .
.
Основные теоремы дискретного преобразования Лапласа
Свойство линейности:
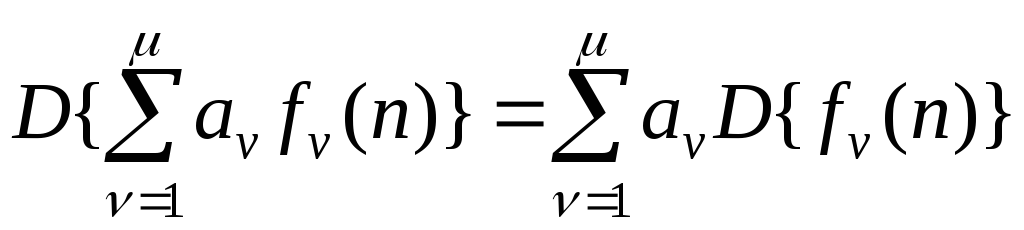 .
.Теорема сдвига:
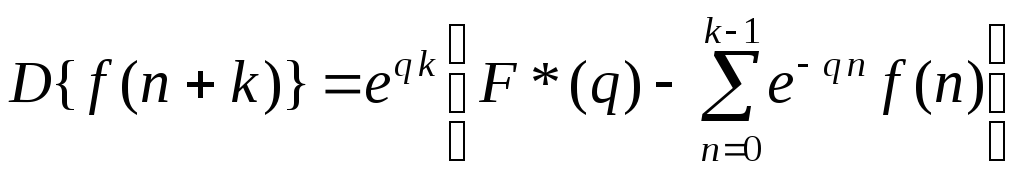 ,
,
![]() .
.
Теорема смещения:
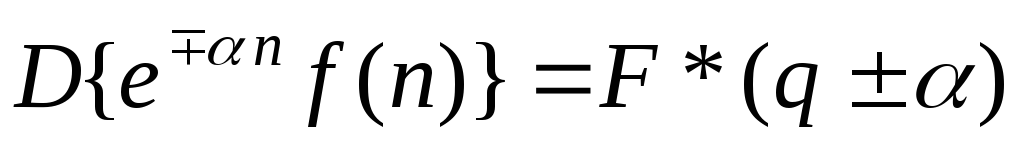 .
.Теорема о дифференцируемости по параметру:
![]() .
.
Теорема об умножении решетчатой функции на
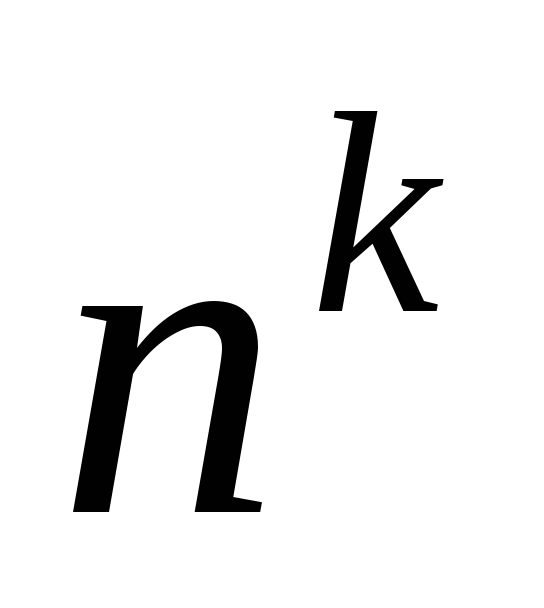 :
:
![]() .
.
Теорема свертывания:
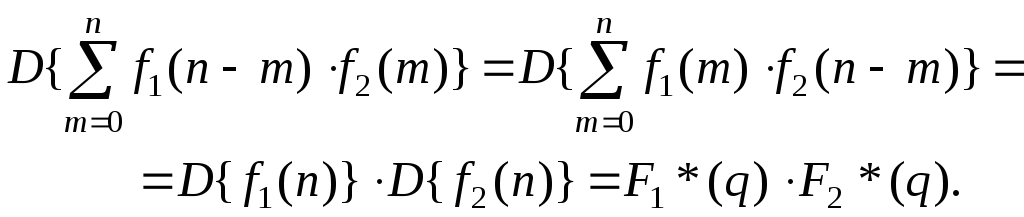
Предельные значения решетчатой функции:
![]() ,
,
![]() .
.
z-преобразование
Если
ввести обозначение
![]() ,
то теорема сдвига примет следующую
форму
,
то теорема сдвига примет следующую
форму![]() .
Здесь
.
Здесь![]() – имеет смысл оператора сдвига,
посредством которого решетчатой функции
– имеет смысл оператора сдвига,
посредством которого решетчатой функции![]() ставится в соответствие та же функция
со сдвинутым аргументом
ставится в соответствие та же функция
со сдвинутым аргументом![]() .
В этом случае дискретное преобразование
Лапласа можно представить следующим
образом
.
В этом случае дискретное преобразование
Лапласа можно представить следующим
образом
![]() . (11.2)
. (11.2)
В этом случае оно называется z-преобразованием. Это преобразование практически совпадает с дискретным преобразованием Лапласа и отличается только аргументом изображения. При такой замене трансцендентные функции от аргумента q преобразуются в рациональные функции от аргумента z.
Отыскание оригиналов по изображениям для дискретного преобразования Лапласа и z-преобразования производится по формулам, подобным формулам, применяемым в случае обычного преобразования Лапласа. В табл. 11.1 приведены некоторые формулы z-преобразования решетчатых функций.
Таблица 11.1
|
|
|
|
1 |
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример 11.1. Решим разностное (рекуррентное) уравнение
![]()
где
![]()
Для этого найдем
![]() -преобразование
этого уравнения
-преобразование
этого уравнения
![]() .
.
Отсюда следует
![]() .
.
Изображение
известной функции ![]() можно представить в виде
можно представить в виде
![]() .
.
Таким образом
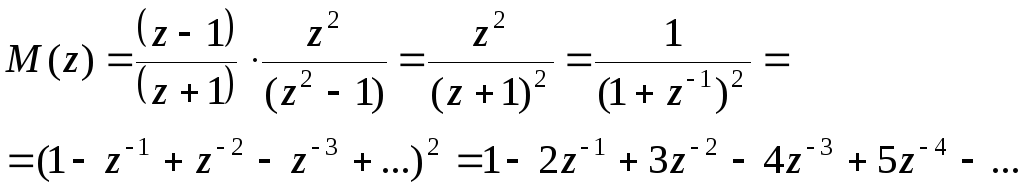
Решетчатая функция равна коэффициентам полученного ряда
![]() .
.
Дискретная интерпретация операционного исчисления Микусиньского
Как
известно, операционное исчисление,
позволяющее сводить дифференциальные
задачи к алгебраическим, возникло
благодаря работам английского ученого
Оливера Хевисайда (1859-1925), который
предложил формальные правила обращения
с дифференциальным оператором
![]() и некоторыми функциями от этого оператора.
Строгое обоснование данного метода
впервые было дано с помощью интегрального
преобразования Лапласа. Однако
использование интеграла Лапласа
наталкивается на ограничения, связанные
с ростом преобразуемой функции
и некоторыми функциями от этого оператора.
Строгое обоснование данного метода
впервые было дано с помощью интегрального
преобразования Лапласа. Однако
использование интеграла Лапласа
наталкивается на ограничения, связанные
с ростом преобразуемой функции![]() при
при![]() .
.
Другой путь предложен польским математиком Я. Микусиньским (1953), опиравшимся на понятие функционального кольца. Метод Микусиньского представляет собой радикальный возврат к первоначальной операторной идее. При использовании этого метода не накладывается никаких ограничений на поведении функций на бесконечности и, следовательно, область применения операционного исчисления Микусиньского значительно шире, чем операционного исчисления, основывающемся на преобразовании Лапласа.
Поскольку обе теории имеют дело с непрерывными функциями, применение операционного исчисления к решению задач имеет характер символьных преобразований. Это сужает возможности метода из-за того, что только достаточно простые задачи допускают решение в символьной форме.
При
использовании численных методов
непрерывные функции аппроксимируют
решетчатыми функциями, которые изменяются
только при целых значениях аргумента
![]() .
К решетчатым функциям можно применять
дискретное преобразование Лапласа,
однако по своей природе оно также более
пригодно для символьных преобразований,
поскольку оперирует бесконечными
суммами.
.
К решетчатым функциям можно применять
дискретное преобразование Лапласа,
однако по своей природе оно также более
пригодно для символьных преобразований,
поскольку оперирует бесконечными
суммами.
Ниже предлагается для численного решения задач на компьютере использовать дискретную форму операционного исчисления Микусиньского, основанную на матричном представлении решетчатых функций и матричных операторах.
Решетчатую функцию
обычно задают в виде бесконечной
последовательности чисел:
![]() ,
,![]() Если для некоторого натурального числа
Если для некоторого натурального числа![]() справедливо
справедливо![]() (
(![]() ),
то тогда решетчатую функцию можно задать
в виде конечной последовательности
чисел:
),
то тогда решетчатую функцию можно задать
в виде конечной последовательности
чисел:
![]() ,
,
![]() . (11.3)
. (11.3)
В этом случае удобно пользоваться векторным представлением решетчатой функции:
![]() . (11.4)
. (11.4)
Обозначения (11.3)
и (11.4) в дальнейшем будем считать
эквивалентными друг другу. Индексы
компонент вектора соответствуют
аргументам решетчатой функции
![]() ,
а сами компоненты
,
а сами компоненты![]() – значениям функции в соответствующих
точках. Множество таких векторов размером
– значениям функции в соответствующих
точках. Множество таких векторов размером![]() обозначим как
обозначим как![]() .
.
Для наших целей
решетчатую функцию вида (11.3) или (11.4)
удобнее представить в виде нижней
треугольной матрицы размером
![]()
 . (11.5)
. (11.5)
Как можно видеть,
первый столбец матрицы
![]() является вектором
является вектором![]() .
Второй получен путем единичного сдвига
всех элементов первого столбца вниз.
Третий – путем двойного сдвига, и т.д.
Освободившиеся места замещаются нулями.
Эквивалентность решетчатой функции
.
Второй получен путем единичного сдвига
всех элементов первого столбца вниз.
Третий – путем двойного сдвига, и т.д.
Освободившиеся места замещаются нулями.
Эквивалентность решетчатой функции![]() матрице
матрице![]() будем обозначать следующим образом:
будем обозначать следующим образом:![]() .
.
Целесообразность
приведенного представления объясняется
тем, что для треугольных матриц сумма
и произведение нижних (верхних) матриц
есть также нижняя (верхняя) треугольная
матрица. Обратный переход от функции-матрицы
![]() к функции-вектору
к функции-вектору![]() осуществляется с помощью следующей
операции
осуществляется с помощью следующей
операции
![]() , (11.6)
, (11.6)
где
![]() – вектор-столбец размером
– вектор-столбец размером![]() (
(![]() ).
).
Множество нижних
треугольных матриц размером
![]() обозначается как
обозначается как![]() .
Множество матриц вида (11.5),
которое мы обозначим как
.
Множество матриц вида (11.5),
которое мы обозначим как
![]() ,
является собственным подмножеством
множества
,
является собственным подмножеством
множества![]() .
.
Свертка
![]() двух решетчатых функций
двух решетчатых функций![]() и
и![]() может быть определена следующим образом:
может быть определена следующим образом:
![]() , (11.7)
, (11.7)
![]() . (11.8)
. (11.8)
Рассмотрим
квадратную матрицу размером
![]() :
:![]() ,
,![]() .
Если
.
Если![]() ,
то
,
то
![]() (11.9)
(11.9)
В этом случае
матрица
![]() обладает свойством:
обладает свойством:
![]() (11.10)
(11.10)
(для любого целого
![]() ,
удовлетворяющего условиям:
,
удовлетворяющего условиям:![]() ,
,![]() ).
Если матрица
).
Если матрица![]() обладает свойством (11.10) и
обладает свойством (11.10) и![]() ,
то очевидно, что
,
то очевидно, что![]() .
.
Теорема 11.1.
Если
![]() и
и![]() ,
то произведение матриц:
,
то произведение матриц:![]() .
.
Доказательство.
Пусть
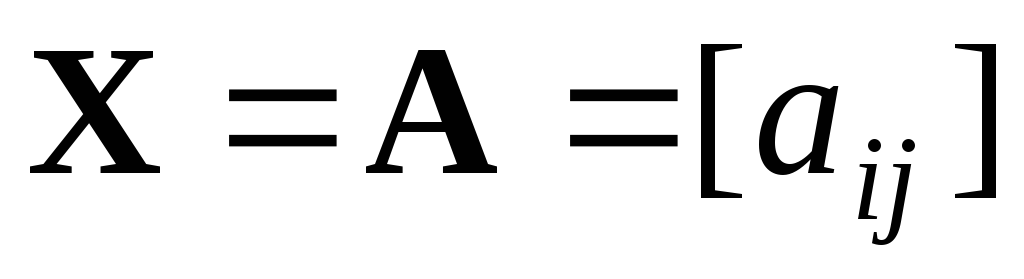 и
и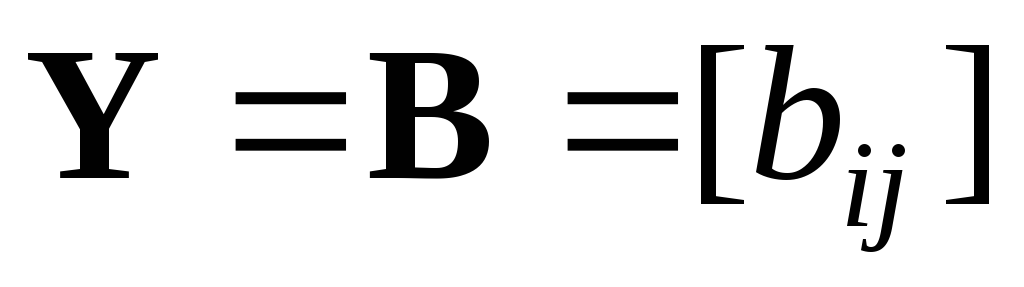 .
Тогда
.
Тогда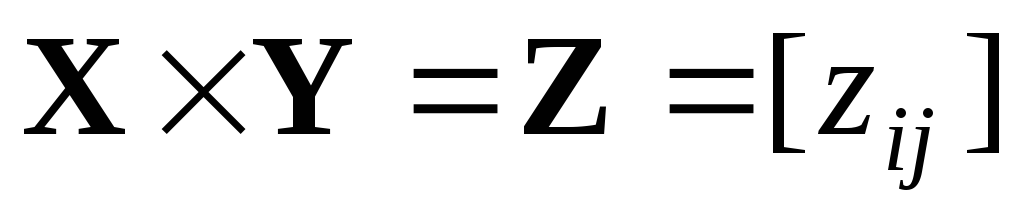 ,
,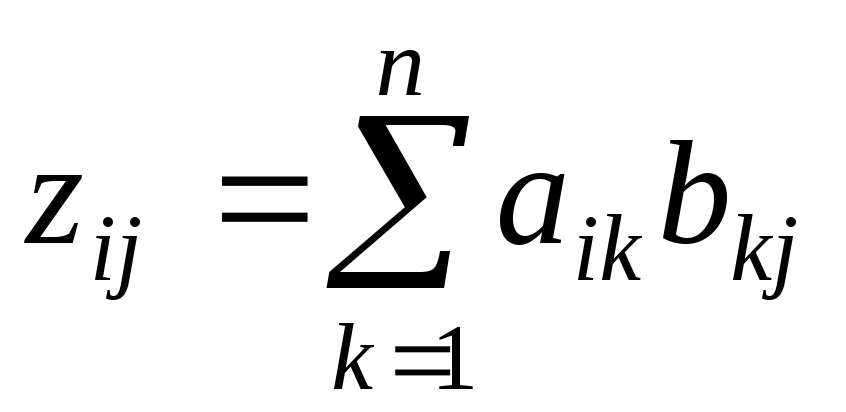 ,
,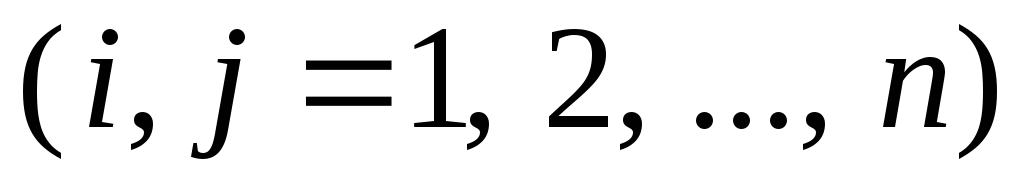 .
.С учетом формулы (11.9):
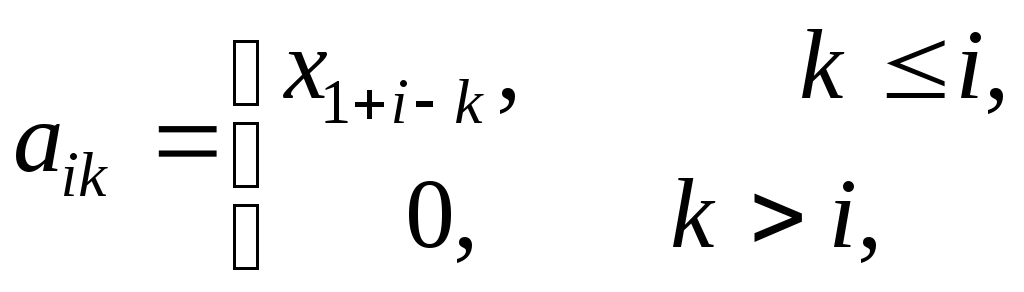
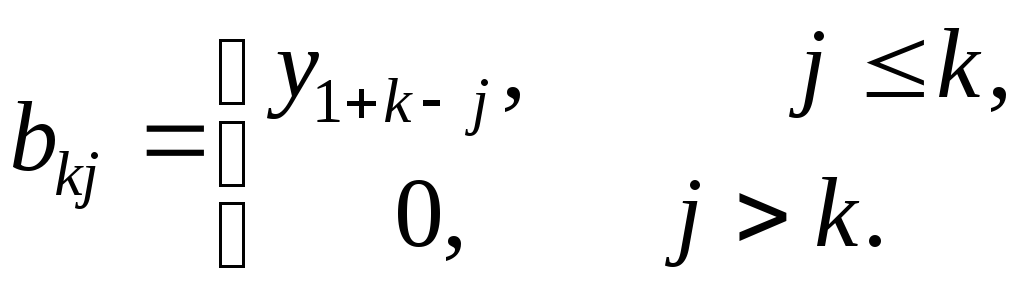
Отсюда следует:
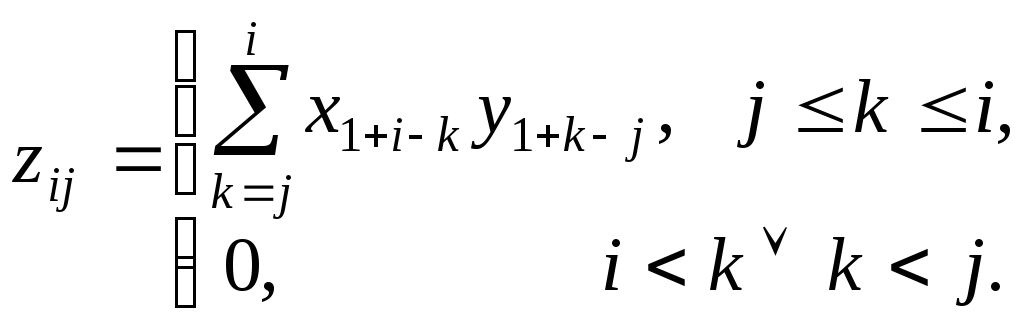
Если
 ,
то
,
то ,
что соответствует определению свертки
(формула (11.8)).
,
что соответствует определению свертки
(формула (11.8)).Если
 ,
то:
,
то: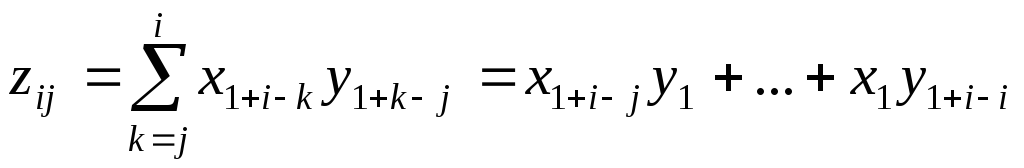 и
и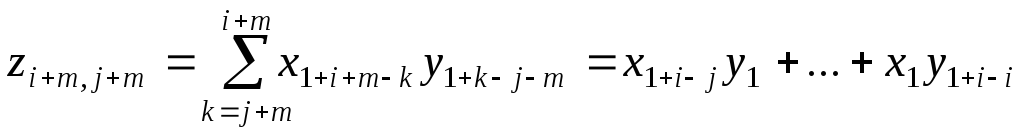 .
Следовательно:
.
Следовательно: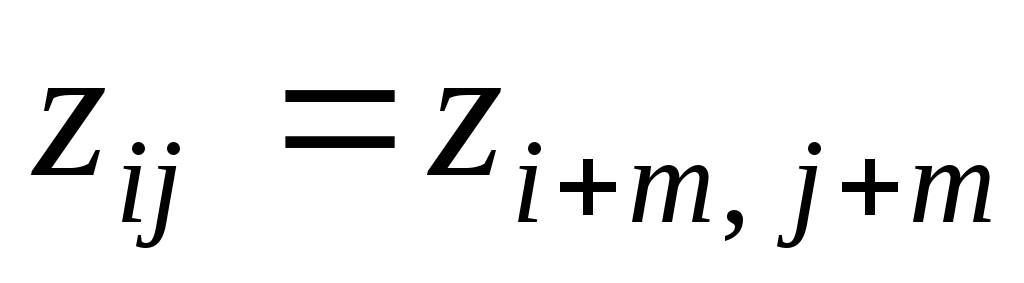 (для любого целого
(для любого целого ,
удовлетворяющего условиям:
,
удовлетворяющего условиям: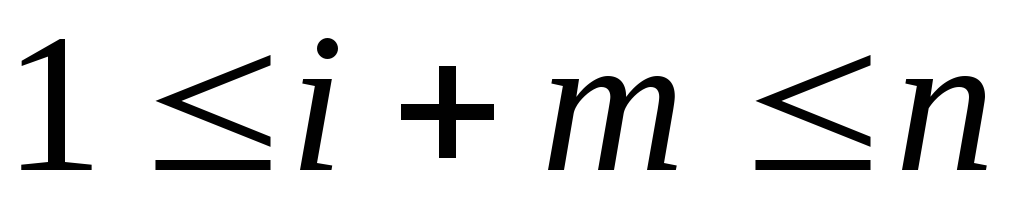 ,
,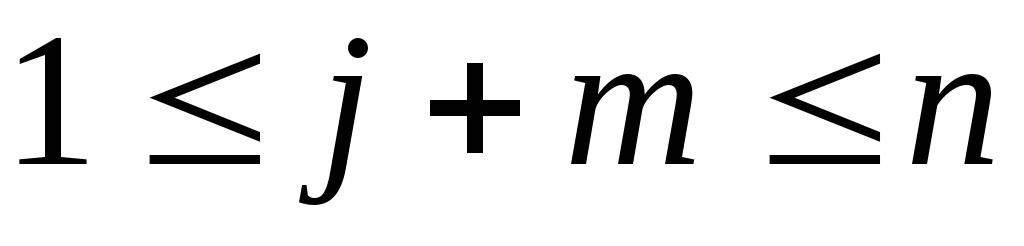 ).
Поэтому:
).
Поэтому: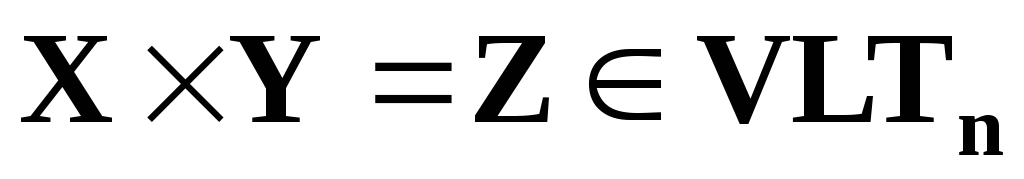 .
.
Теорема доказана.
Следствие.
Множество
![]() является кольцом по сложению и умножению,
и умножение коммутативно (поскольку
операция свертки коммутативна). Единичную
матрицу будем обозначать как
является кольцом по сложению и умножению,
и умножение коммутативно (поскольку
операция свертки коммутативна). Единичную
матрицу будем обозначать как![]() ,
нулевую:
,
нулевую:![]() .
.
Рассмотрим нижнюю
треугольную матрицу
![]() ,
ненулевые элементы которой, равные
единице, расположены под главной
диагональю:
,
ненулевые элементы которой, равные
единице, расположены под главной
диагональю:
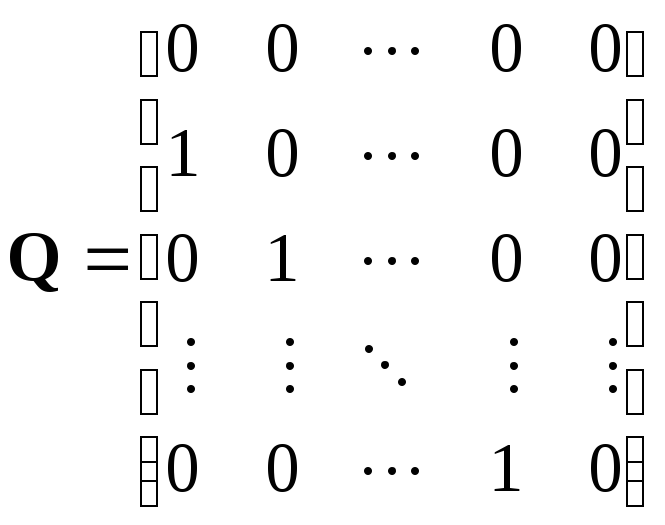 . (11.11)
. (11.11)
То есть
![]()
Если эту матрицу
умножить на матрицу
![]() ,
то элементы произведения окажутся
смещенными на одну строку вниз по
сравнению с положением элементов матрицы
,
то элементы произведения окажутся
смещенными на одну строку вниз по
сравнению с положением элементов матрицы![]() ,
а освободившиеся места замещаются
нулями.
,
а освободившиеся места замещаются
нулями.
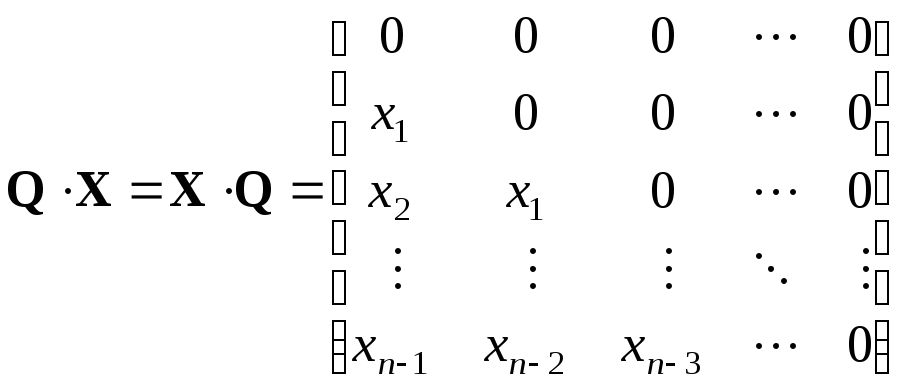 .
.
Поэтому мы будем
называть матрицу
![]() оператором
сдвига. С
помощью оператора сдвига можно выразить
матрицу
оператором
сдвига. С
помощью оператора сдвига можно выразить
матрицу
![]() через компоненты вектора
через компоненты вектора![]() :
:
![]() , (11.12)
, (11.12)
где
![]() – единичная матрица.
– единичная матрица.
Если принять
![]() ,
то (10.12) можно переписать в виде
,
то (10.12) можно переписать в виде
![]() . (11.13)
. (11.13)
Теорема 11.2.
Если
матрица
![]() имеет размер
имеет размер![]() ,
то
,
то
![]() ,
,
![]() (10.14)
(10.14)
Доказательство.
Все элементы
матрицы
![]() равны нулю, за исключением одного. Это
элемент в нижнем левом углу, который
равен единице. Поскольку матрица
равны нулю, за исключением одного. Это
элемент в нижнем левом углу, который
равен единице. Поскольку матрица![]() действует как оператор сдвига, то
действует как оператор сдвига, то![]() .
Далее, переходя к произведению
.
Далее, переходя к произведению![]() (и всем следующим за ним), учитываем, что
результатом перемножения матрицы на
нулевую матрицу является нулевая
матрица.
(и всем следующим за ним), учитываем, что
результатом перемножения матрицы на
нулевую матрицу является нулевая
матрица.
Следствие.
Матрицу
![]() можно представить в виде бесконечного
степенного ряда
можно представить в виде бесконечного
степенного ряда
![]() . (11.15)
. (11.15)
Замечание.
Рассмотрим матрицу
![]() .
Из формулы (11.15) следует
.
Из формулы (11.15) следует
![]() .
.
Формально матрица
![]() – этопроизводящая
функция
последовательности чисел
– этопроизводящая
функция
последовательности чисел
![]() ,
аргументом которой является
,
аргументом которой является![]() .
Как сказал американский ученый Д. Гиббс:
«Математика есть искусство называть
разные предметы одним именем». Символы
.
Как сказал американский ученый Д. Гиббс:
«Математика есть искусство называть
разные предметы одним именем». Символы![]() вz-преобразованиях
и
вz-преобразованиях
и
![]() в матричных уравнениях эквивалентны
друг другу, что позволяет использовать
формулы
z-преобразования
в дискретном операционном исчислении.
Однако, поскольку
в матричных уравнениях эквивалентны
друг другу, что позволяет использовать
формулы
z-преобразования
в дискретном операционном исчислении.
Однако, поскольку
![]() ,
то
,
то![]() не имеет обратной матрицы.
не имеет обратной матрицы.
Теорема 11.3.
![]() ,
(
,
(![]() ). (11.16)
). (11.16)
Доказательство. Из формул (10.12) и (10.14) следует что
![]() .
.
Учитывая действие
матрицы
![]() как оператора сдвига, приходим к формуле
(11.16).
как оператора сдвига, приходим к формуле
(11.16).
Теорема 11.4.
Если
![]() – произвольная квадратная матрица, то
– произвольная квадратная матрица, то
![]() . (11.17)
. (11.17)
Доказательство.
Умножая
обе части уравнения (11.17) справа на
![]() ,
приходим к тождеству
,
приходим к тождеству
![]() .
.
Следствие.
Если
![]() ,
то справедлива формула
,
то справедлива формула
![]() . (11.18)
. (11.18)
Формула (11.18) непосредственно следует из формул (11.17) и (11.14).
Рассмотрим матрицу
![]() ,
определяемую следующим образом:
,
определяемую следующим образом:
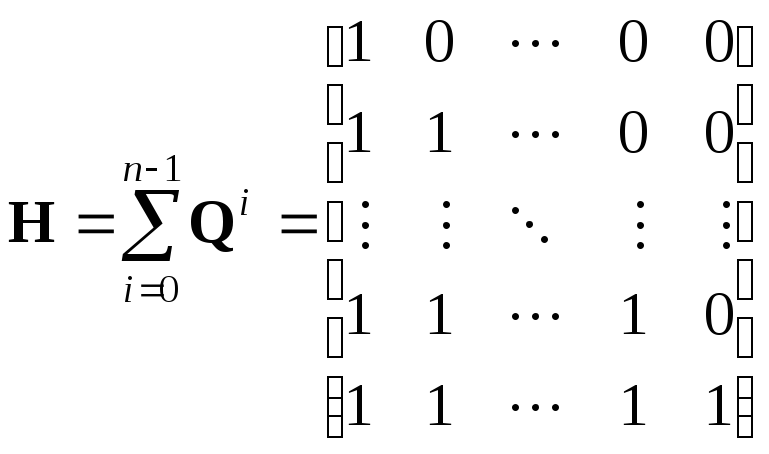 .
(11.19)
.
(11.19)
Теорема 11.5.
Если
![]() ,
то
,
то
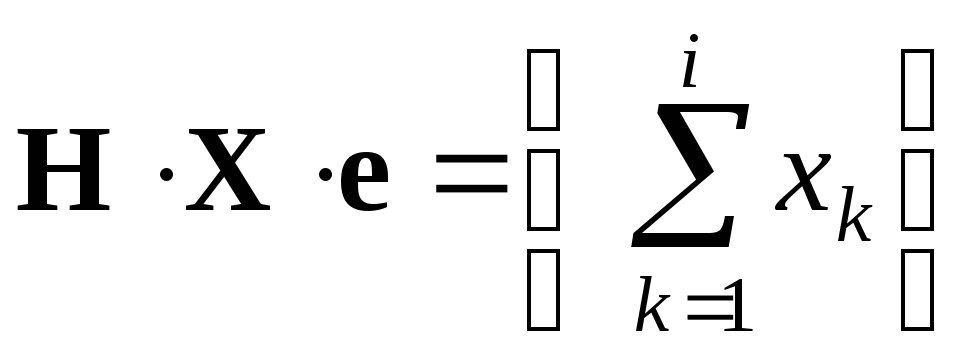 ,
(
,
(![]() ). (11.20)
). (11.20)
Доказательство. На основании определения (11.12) и (11.19) можем записать:
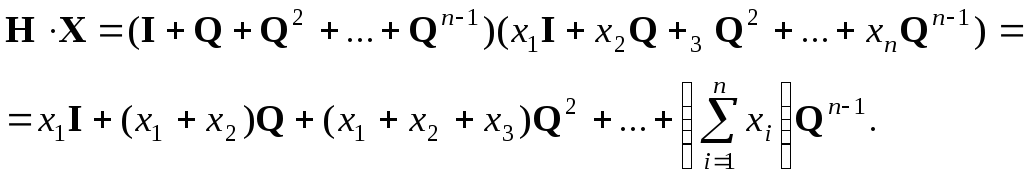
Далее, учитывая
действие матрицы
![]() как оператора сдвига и формулу (11.6),
приходим к формуле (11.20).
как оператора сдвига и формулу (11.6),
приходим к формуле (11.20).
В силу свойства
(11.20) матрицу
![]() будем называтьоператором
суммирования.
Оператор
будем называтьоператором
суммирования.
Оператор
![]() является дискретным аналогом оператора
интегрирования
является дискретным аналогом оператора
интегрирования![]() в операционном исчислении Микусиньского.
в операционном исчислении Микусиньского.
Оператором
вычитания
![]() назовем матрицу, определяемую выражением
назовем матрицу, определяемую выражением
 . (11.21)
. (11.21)
Теорема 11.6.
![]() . (11.22)
. (11.22)
Доказательство. Согласно формуле (11.18):
![]() .
.
Оператор
![]() является дискретным аналогом оператора
дифференцирования
является дискретным аналогом оператора
дифференцирования![]() в операционном исчислении Микусиньского.Конечная
разность
может быть определена следующим образом:
в операционном исчислении Микусиньского.Конечная
разность
может быть определена следующим образом:
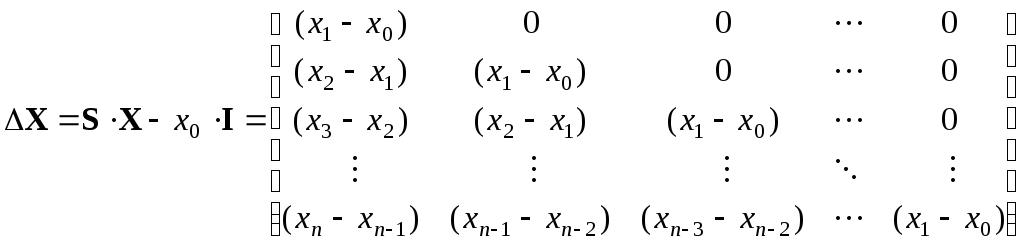 .
.
Теоремы дискретного операционного исчисления
Теоремам непрерывного операционного исчисления можно поставить в соответствие теоремы дискретного операционного исчисления. Приведем несколько таких теорем.
Теорема 11.7.
Если
![]() – произвольное комплексное число, то
– произвольное комплексное число, то
![]() ,
(
,
(![]() ). (11.23)
). (11.23)
Доказательство.
![]()
![]() .
.
Замечание.
Если
![]() ,
то
,
то
![]() .
.
Теорема 11.8.
![]() ,
(
,
(![]() ). (11.24)
). (11.24)
Доказательство.
Используя
формулу (11.20), получим
![]() ,
далее
,
далее![]() ,
,![]() и т.д.
и т.д.
Теорема 11.9.
![]() ,
(
,
(![]() ). (11.25)
). (11.25)
Доказательство.
![]() .
.
Теорема
11.10. Если
![]() – произвольное комплексное число, то
– произвольное комплексное число, то
![]() ,
(
,
(![]() ). (11.26)
). (11.26)
Доказательство.
![]()
Замечание 11.1.
Если
![]() ,
то
,
то
![]() . (11.27)
. (11.27)
Следствие: Используя формулы, выражающие гиперболические и тригонометрические функции через экспоненциальную функцию
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
приходим к следующим уравнениям:
![]() ,
(11.28)
,
(11.28)
![]() , (11.29)
, (11.29)
![]() ,
(11.30)
,
(11.30)
![]() , (11.31)
, (11.31)
(![]() ).
).
Замечание 11.2.
Если
![]() ,
то
,
то
![]() ,
(11.32)
,
(11.32)
![]() , (11.33)
, (11.33)
![]() ,
(11.34)
,
(11.34)
![]() . (11.35)
. (11.35)
Эти приближенные
формулы похожи на точные формулы
непрерывного операционного исчисления,
но здесь вместо оператора дифференцирования
используется оператор вычитания
![]() ,
а вместо единичного оператора – оператор
,
а вместо единичного оператора – оператор![]() .
Формулы (11.27) и (11.32)-(11.35) позволяют
использовать дискретное операционное
исчисление для численного решения задач
непрерывного операционного исчисления.
.
Формулы (11.27) и (11.32)-(11.35) позволяют
использовать дискретное операционное
исчисление для численного решения задач
непрерывного операционного исчисления.
Применение дискретного операционного исчисления
Преимуществом дискретного операционного исчисления является то, что его можно использовать как численный метод, а не только как символьные преобразования. При этом оно опирается на хорошо отработанную технологию матричных преобразований и алгоритмов. Например, можно использовать такую популярную программу технических вычислений, как MATLAB.
Спектр возможных приложений достаточно широк. Дискретное операционное исчисление можно использовать для численного (либо символьного) решения конечно-разностных уравнений. Рассмотрим следующий пример. Решим разностное (рекуррентное) уравнение при нулевых начальных условиях
![]()
где
![]()
Для этого перейдем к матричному представлению этого уравнения, используя теорему 11.3:
![]() ,
,
где
![]() .
.
Отсюда следует
![]()
Таким образом
![]() .
.
Численный метод решения той же задачи с помощью MATLAB приведен ниже.
>> A=Q*Q;
>> SUM=NULL;
>> for k=1:100
SUM=SUM+A^k;
end
>> E=I+SUM;
>> M=E*(I-Q)*inv(I+Q);
Кроме
того, дискретное операционное исчисление
можно использовать как численный метод
решения задач непрерывной математики.
Особенностью использования операционного
метода для решения дифференциальных
уравнений является то, что получить
изображение неизвестной функции обычно
не очень сложно. Трудности возникают
на этапе получения оригинала этого
изображения. Во многих случаях оригинал
определяется только численно. И здесь
может оказаться полезным дискретное
операционное исчисление, в котором
оператор дифференцирования
![]() приближенно заменяется матричным
оператором
приближенно заменяется матричным
оператором![]() .
Это возможно в случаях, когда функция,
являющаяся решением задачи, незначительно
изменяется при увеличении аргумента
.
Это возможно в случаях, когда функция,
являющаяся решением задачи, незначительно
изменяется при увеличении аргумента![]() на единицу. Можно подобрать период
дискретизации решетчатой функции таким
образом, чтобы это условие выполнялось.
Для порождающей функции
на единицу. Можно подобрать период
дискретизации решетчатой функции таким
образом, чтобы это условие выполнялось.
Для порождающей функции![]() ,
аргументом которых является произведение:
,
аргументом которых является произведение:![]() ,
где
,
где![]() – переменная, а
– переменная, а![]() – параметр, это условие эквивалентно
требованию малости модуля параметра
по сравнению с единицей:
– параметр, это условие эквивалентно
требованию малости модуля параметра
по сравнению с единицей:![]() .
Используя разложение функции
.
Используя разложение функции![]() в окрестности точки
в окрестности точки![]() в ряд Тейлора, получим:
в ряд Тейлора, получим:
![]() .
.
Обычно
![]() .
Таким образом, чем меньше по модулю
параметр
.
Таким образом, чем меньше по модулю
параметр![]() ,
тем меньше приращение функции
,
тем меньше приращение функции![]() .
Хотя такой подход не может обеспечить
абсолютно точного решения (как и любой
другой численный метод), однако результат
во многих случаях имеет приемлемую
точность. Необходимо только при переходе
от непрерывного изображения к матричному
его представлению вместо единичной
матрицы
.
Хотя такой подход не может обеспечить
абсолютно точного решения (как и любой
другой численный метод), однако результат
во многих случаях имеет приемлемую
точность. Необходимо только при переходе
от непрерывного изображения к матричному
его представлению вместо единичной
матрицы![]() использовать матрицу
использовать матрицу![]() .
.
Ниже дан пример
решения дифференциального уравнения
![]() при нулевых начальных условиях. Для
сравнения приводится точное решение,
полученное аналитическим методом.
при нулевых начальных условиях. Для
сравнения приводится точное решение,
полученное аналитическим методом.
Y=inv(S*(25*S^2+0.5*S+Q));
OutM=Y*Ve;
plot(OutM), hold on
for k=1:100
Out(k)=1- exp(-0.01*k)*(cos(0.19975*k)
+0.05*sin(0.19975*k));
end
plot(Out), hold on

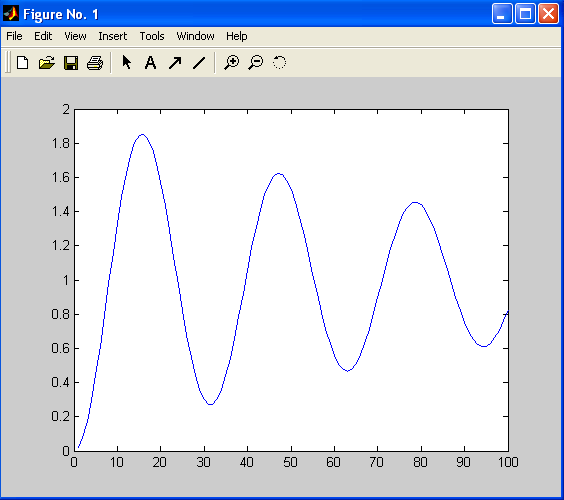
Рис. 11.2
Как можно видеть,
для решения задачи достаточно набрать
небольшое число команд. В результате
получим графики функции
![]() ,
соответствующие матричному и точному
решению. Они показаны на рис. 11.2. Как
можно видеть, отклонения от точного
решения едва заметны. В данном случае
использовалась матрица
,
соответствующие матричному и точному
решению. Они показаны на рис. 11.2. Как
можно видеть, отклонения от точного
решения едва заметны. В данном случае
использовалась матрица![]() размером
размером![]() =100.
По меркамMATLAB
это не очень большая матрица, и результат
отображается на экране мгновенно.
Идентификатор Ve
в программе
обозначает вектор
=100.
По меркамMATLAB
это не очень большая матрица, и результат
отображается на экране мгновенно.
Идентификатор Ve
в программе
обозначает вектор
![]() .
.
С помощью дискретного
операционного исчисления можно решать
не только обыкновенные дифференциальные
уравнения, но и уравнения в частных
производных. В этом случае функция-изображение
является иррациональной функцией
![]() и может содержать члены вида
и может содержать члены вида![]() или
или![]() ,
где
,
где![]() – нецелое действительное число. Для
получения матриц
– нецелое действительное число. Для
получения матриц![]() необходимо использовать общую биномиальную
теорему из теории аналитических функций.
необходимо использовать общую биномиальную
теорему из теории аналитических функций.
![]() . (11.36)
. (11.36)
В частном случае
![]() имеем
имеем
![]() (11.37)
(11.37)
Результат разложения
(11.37) легко проверить умножением:
![]() .
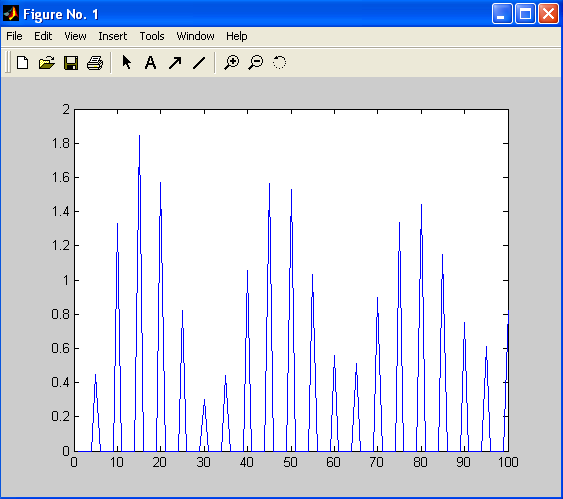
На рис. 11.3 показаны графики функции
.
На рис. 11.3 показаны графики функции![]() ,
изображением которой является функция
,
изображением которой является функция![]() (матричное решение и точное). Эти графики
получены с помощью следующей программыMATLAB.
(матричное решение и точное). Эти графики
получены с помощью следующей программыMATLAB.
for k=1:100
Out(k)=1/(sqrt(3.141592654*k));
end
>> a=1;
>> Qk=I;
>> Sum=NULL;
>> for k=1:100
Qk=Qk*Q;
a=a*abs(2*k-3)/(2*k);
Sum=Sum+a*Qk;
end
>> SRS=I-Sum;
Y=inv(SRS);
>> OutM=Y*Ve;
>> plot(OutM), hold on
>> plot(Out), hold on
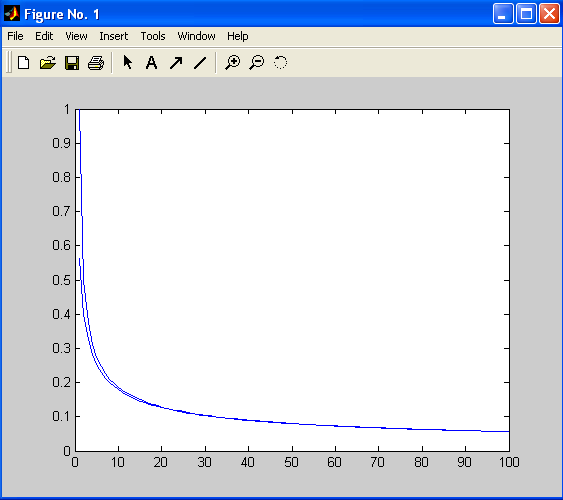
Рис. 11.3
В начале этой
программы вычисляется точное значение
искомой функции. Затем находится матрица
![]() и обратная ей матрица. ИдентификаторSRS
соответствует матрице
и обратная ей матрица. ИдентификаторSRS
соответствует матрице
![]() ,
а идентификаторNULL
– матрице с нулевыми элементами.
,
а идентификаторNULL
– матрице с нулевыми элементами.
