
- •Санкт-Петербург
- •Задачи студенческой математической олимпиады Северо-Запада России
- •19 Мая 2013 года
- •Решения задач
- •Результаты в командном зачете:
- •Ранжированный список команд вузов участников студенческой олимпиады Северо-Запада России по математике 2013 года.
- •Ранжированный список участников студенческой олимпиады Северо-Запада России по математике 2013 года.
Министерство образования и науки Российской Федерации
Санкт-Петербургский национальный исследовательский
университет информационных технологий,
механики и оптики
Студенческая математическая олимпиада
Северо-Запада России
2013г.

Санкт-Петербург
2013
В 2013 г. студенческая олимпиада Северо-Запада России по математике проводилась Санкт-Петербургским национальным исследовательским университетом информационных технологий, механики и оптики (НИУ ИТМО). Каждый вуз мог выставить одну команду из трех человек (в командный зачет входили все участники команды) и студентов в личный зачет. В личном зачете участвовали все заявленные студенты. Результат вуза в командном зачете определялся по результату его команды.
Олимпиада проводилась в воскресенье 19 мая 2013 года. На решение задач отводилось 4 часа. Пользоваться справочной литературой не разрешалось. Студентам всех групп было предложено 12 задач. Каждая задача оценивалась в 10 баллов.
Председателем жюри был профессор СПбГУ Н.А. Широков. В оргкомитет олимпиады входили: ректор НИУ ИТМО, проф., д.т.н. Васильев В.Н., проф., д.ф.-м.н Попов И.Ю., доц., к.ф.-м.н. Фролов В.М. доц., к.ф.-м.н. Трифанова Е.С, доц., к.т.н. Блинова И.В., асс., к.ф.-м.н. Трифанов А.И.,
Составители: проф., д.ф.-м.н. Н.А. Широков, проф., д.ф.-м.н. Попов И.Ю., доц.: к.ф.-м.н. Фролов В.М., к.ф.-м.н. Рыжков А.Е., к.ф.-м.н. Трифанова Е.С, к.т.н. Блинова И.В., ст. преп. Родина Т.В., асс., к.ф.-м.н. Трифанов А.И., асс. Петтай П.П.
Задачи студенческой математической олимпиады Северо-Запада России
19 Мая 2013 года
1.
Верно ли, что для любой непрерывной на
![]() функции
функции![]() найдутся такие непрерывные функции
найдутся такие непрерывные функции![]() ,
что для всех вещественныхx
выполнено:
,
что для всех вещественныхx
выполнено:
![]() ?
?
2.
Найти функцию ![]() ,
если известно, что
,
если известно, что ![]() ,
,
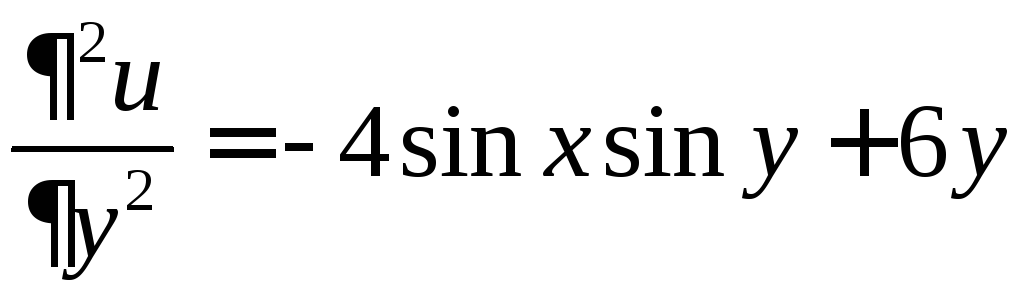 ,
,
![]() ,
,
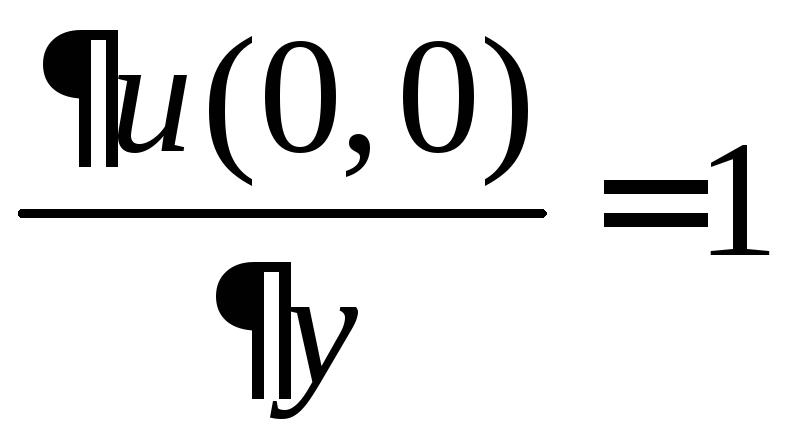 .
.
3.
а)
Существует ли полином ![]() с вещественными коэффициентами такой,
что
с вещественными коэффициентами такой,
что 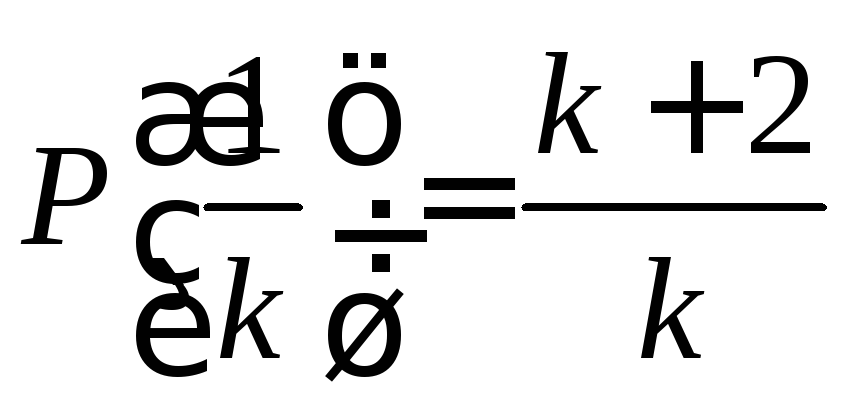 для любого натурального k?
для любого натурального k?
б)
Существует ли полином ![]() с вещественными коэффициентами такой,
что
с вещественными коэффициентами такой,
что 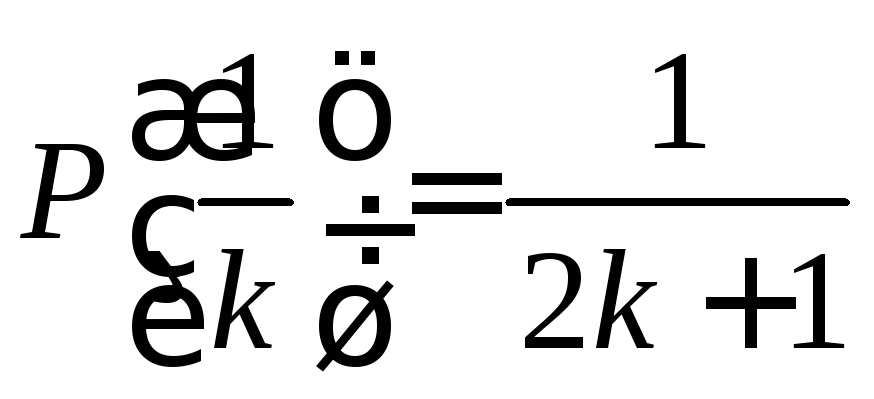 для любого натурального k?
для любого натурального k?
4.
Найти расстояние по поверхности между
городами Санкт-Петербург (северная
широта ![]() ,
восточная долгота
,
восточная долгота ![]() )
и Ханчжоу (Китай) (северная широта
)
и Ханчжоу (Китай) (северная широта ![]() ,
восточная долгота
,
восточная долгота ![]() ).
Землю считать шаром радиуса
).
Землю считать шаром радиуса ![]() км.,
км., 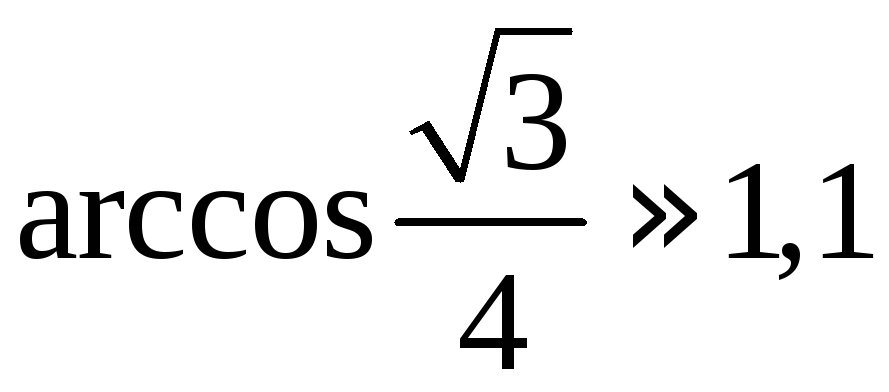
6.
Вектор
![]() разрешается умножать слева на любую из
трех матриц
разрешается умножать слева на любую из
трех матриц
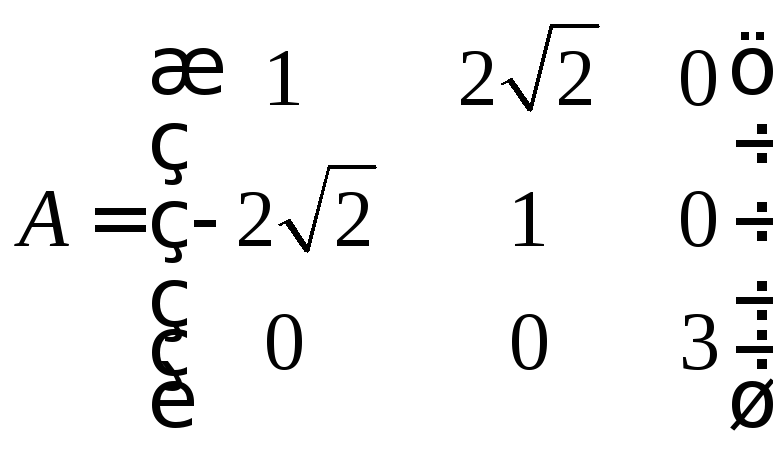 ,
,
 ,
,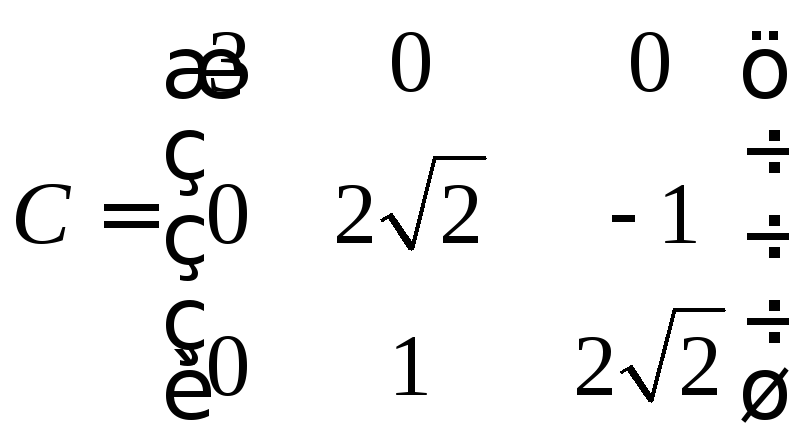 сколько угодно раз в произвольном
порядке (например, можно получить вектор
сколько угодно раз в произвольном
порядке (например, можно получить вектор![]() ).
Можно ли из вектора
).
Можно ли из вектора
![]() с помощью таких преобразований получить
вектор
с помощью таких преобразований получить
вектор![]() ?
?
7.
Сходится или расходится следующий
интеграл: 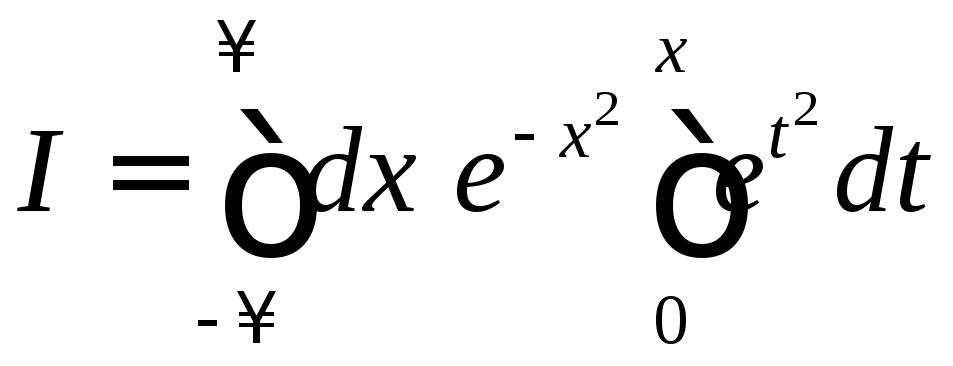 ?
?
8.
Доказать, что любое решение дифференциального
уравнения ![]() ограничено.
ограничено.
9.
Известно, что члены последовательности
![]() удовлетворяют условию
удовлетворяют условию![]() для любых
для любых![]() .
Показать, что
.
Показать, что![]() – неограниченная последовательность.
– неограниченная последовательность.
10.
Последовательность
![]() задана рекуррентно:
задана рекуррентно:![]() ,
,![]() ,
,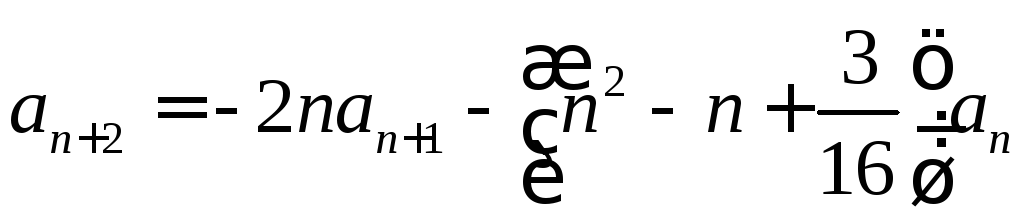 ,
,![]() .
Найти сумму ряда
.
Найти сумму ряда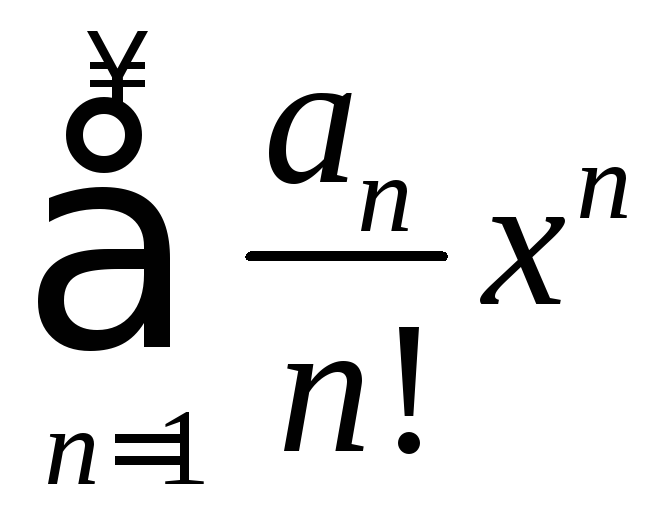 .
.
11.
Пусть ![]() и
и ![]() - две
- две ![]() матрицы с целыми элементами такие, что
матрицы
матрицы с целыми элементами такие, что
матрицы ![]() ,
,
![]() ,
,
![]() ,
…
,
… ![]() обратимы и у их обратных матриц все
элементы целые. Показать, что
обратимы и у их обратных матриц все
элементы целые. Показать, что ![]() также обратима и все элементы ее обратной
матрицы целые.
также обратима и все элементы ее обратной
матрицы целые.
12.
Пусть
![]() - непрерывная функция
- непрерывная функция![]() ,
,
![]() ,
,
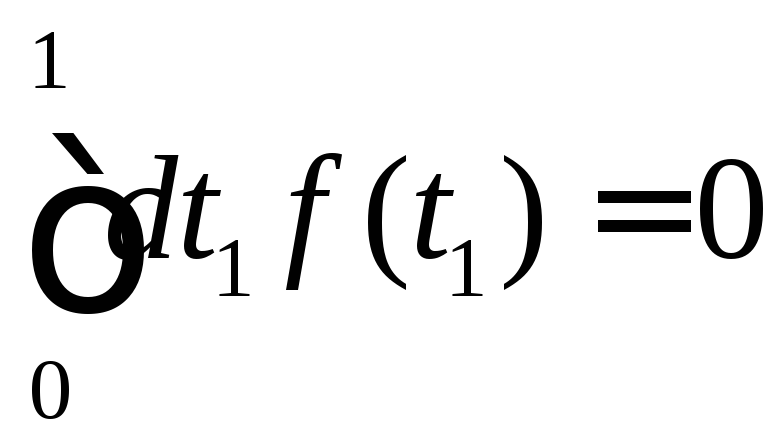 ,
…
,
…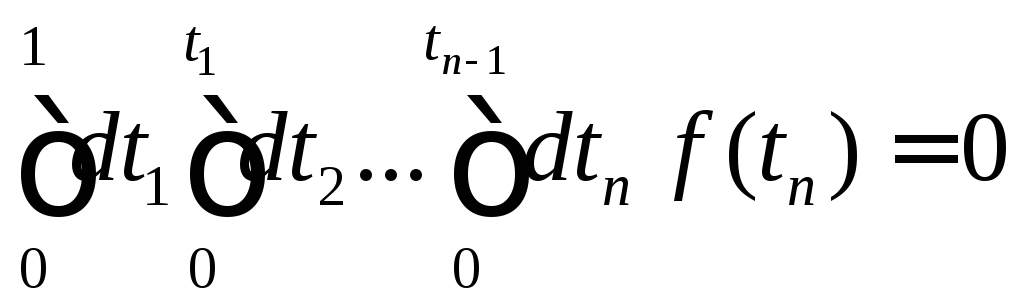 ,
,![]() .Найти
.Найти
 .
.
Решения задач
1.
Да.
Например,
![]()
2.
Из выражения для ![]() из условия следует
из условия следует ![]() ,
откуда находим
,
откуда находим 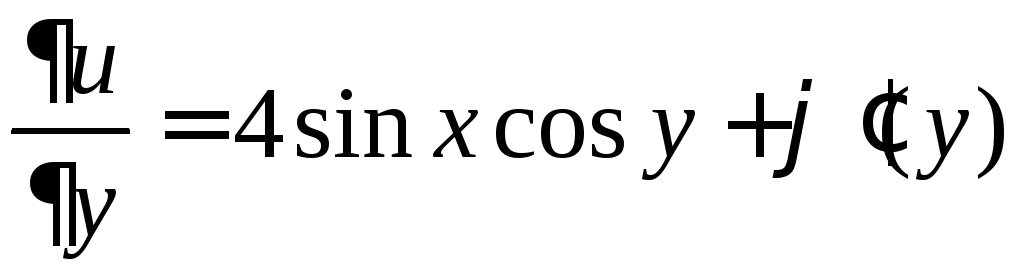 ,
,
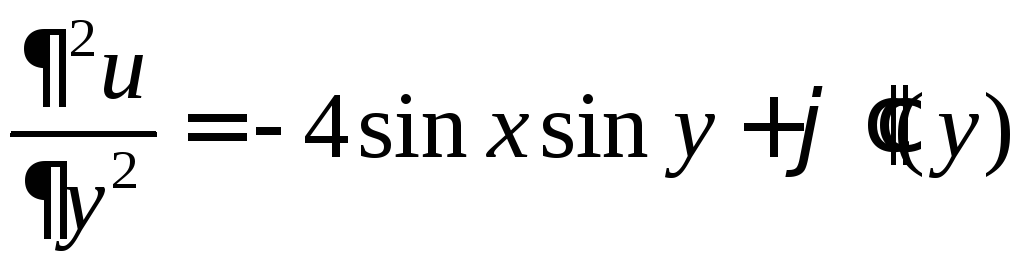 .
Сравнивая выражения для
.
Сравнивая выражения для ![]() из условия с найденным, заключаем, что
из условия с найденным, заключаем, что
![]() ,
т.е.
,
т.е. ![]() .
Используя начальные условия, находим,
что
.
Используя начальные условия, находим,
что ![]() .
Поэтому окончательно получаем
.
Поэтому окончательно получаем ![]() .
.
3.
а)
Да. ![]() .
.
б)
Нет. Допустим, такой полином ![]() существует. Определим полином
существует. Определим полином ![]() :
:
![]() .
.
Тогда
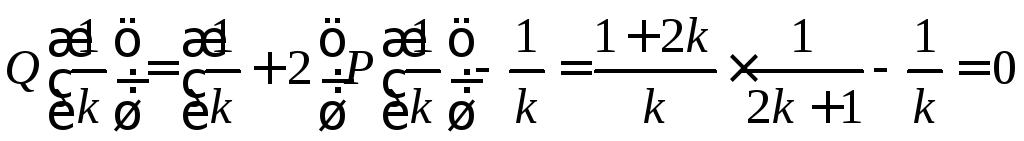 для всех
для всех ![]() .
.
Значит,
полином ![]() имеет бесконечно много корней.
Следовательно, он тождественно равен
нулю:
имеет бесконечно много корней.
Следовательно, он тождественно равен
нулю: ![]() .
Значит,
.
Значит, ![]() для всех x,
для всех x,
![]() .
.
Противоречие, т.к. это не полином.
4.
![]() ,
,
![]() ,
,
![]() ,
где
,
где ![]() - долгота,
- долгота, ![]() - широта (отсчет от экватора, т.е. от
плоскости
- широта (отсчет от экватора, т.е. от
плоскости ![]() ).
Расстояние между городами
).
Расстояние между городами ![]() равно длине дуги большого круга
равно длине дуги большого круга ![]() ,
т.е.
,
т.е. ![]() ,
где
,
где ![]() ,
O
- центр Земли,
,
O
- центр Земли, ![]() -
ее радиус. Имеем
-
ее радиус. Имеем ![]() ,
,
![]() .
.
![]() .
.
Так
как ![]() ,
,
![]() ,
,
![]() .
Следовательно,
.
Следовательно, ![]() ,
т.е.
,
т.е. ![]() .
.
Ответ:
 (км.).
(км.).
5.
Могут ли функции
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() быть на
быть на![]() различными частными решениями одного
и того же линейного однородного
дифференциального уравнения 2013 порядка
с непрерывными коэффициентами и
положительным коэффициентом при старшей
производной?
различными частными решениями одного
и того же линейного однородного
дифференциального уравнения 2013 порядка
с непрерывными коэффициентами и
положительным коэффициентом при старшей
производной?
5.
Нет.
Линейная комбинация решений есть
решение. Если данный набор – решения,
то решениями будут и
![]() .
Вронскиан этой системы 2013 функций равен
.
Вронскиан этой системы 2013 функций равен
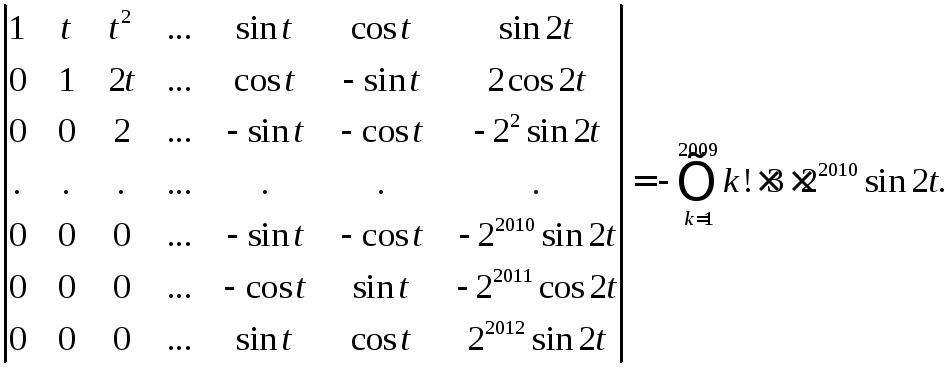
Однако вронскиан n решений линейного дифференциального уравнения n-ого порядка либо тождественно равен нулю, либо не обращается в нуль ни в одной точке. Противоречие.
Замечание. Можно непосредственно искать коэффициенты уравнения, последовательно подставляя данные функции, и тоже прийти к противоречию.
6.
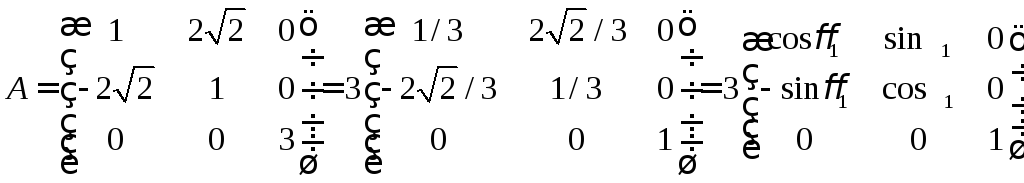 ,
,
следовательно,
оператор умножения на матрицу
![]() поворачивает любой вектор на угол
поворачивает любой вектор на угол![]() вокруг оси аппликат и растягивает его
в 3 раза. Аналогично,
вокруг оси аппликат и растягивает его
в 3 раза. Аналогично,
 ,
,
т.е.
умножение на матрицу
![]() поворачивает любой вектор на угол
поворачивает любой вектор на угол![]() вокруг оси ординат и сжимает его в 2
раза. Аналогично,
вокруг оси ординат и сжимает его в 2
раза. Аналогично,
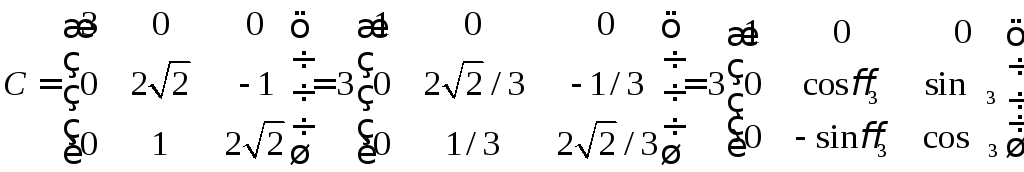 ,
,
т.е.
умножение на матрицу
![]() поворачивает любой вектор на угол
поворачивает любой вектор на угол![]() вокруг оси ординат и растягивает его в
3 раза.
вокруг оси ординат и растягивает его в
3 раза.
С
помощью композиции таких преобразований
мы можем растянуть вектор в ![]() раз и сжать его в
раз и сжать его в ![]() раз. Квадрат длины вектора
раз. Квадрат длины вектора ![]() ,
квадрат длины вектора
,
квадрат длины вектора ![]() .
Таким образом, необходимым условием
возможности преобразования вектора
.
Таким образом, необходимым условием
возможности преобразования вектора ![]() в вектор
в вектор ![]() является разрешимость в целых
неотрицательных числах уравнения
является разрешимость в целых
неотрицательных числах уравнения ![]() ,
т.е.
,
т.е. ![]() ,
однако данное уравнение решений не
имеет, т.к. правая часть делится на 5, а
левая нет.
,
однако данное уравнение решений не
имеет, т.к. правая часть делится на 5, а
левая нет.
7.
Интеграл расходится. Для доказательства
достаточно показать, что 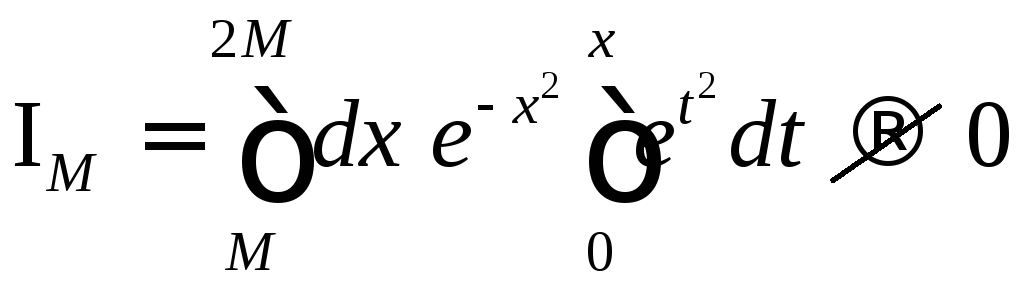 при
при ![]() .
Сделаем замену переменной
.
Сделаем замену переменной ![]() .
Тогда
.
Тогда  .
Поскольку
.
Поскольку ![]() ,
то
,
то

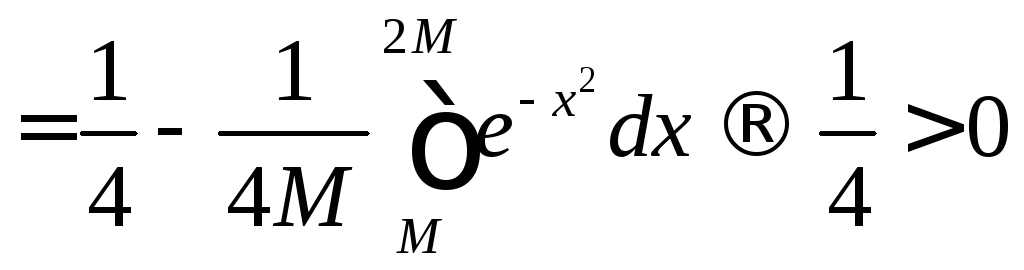 ,
,
т.к.
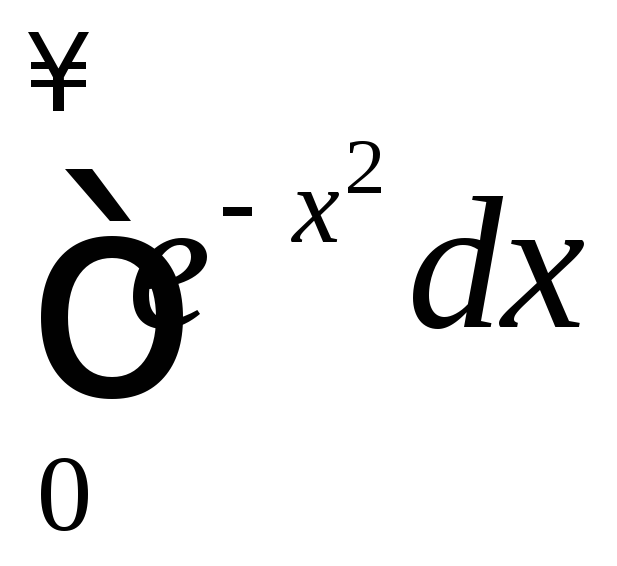 сходится (это известно, см., например,
сходится (это известно, см., например, 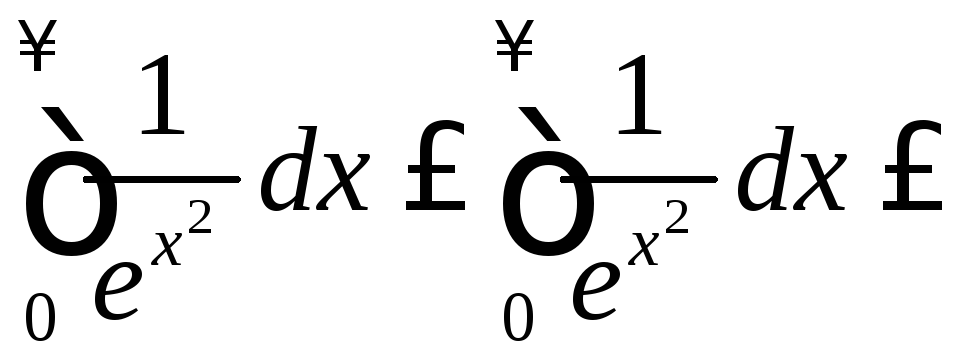
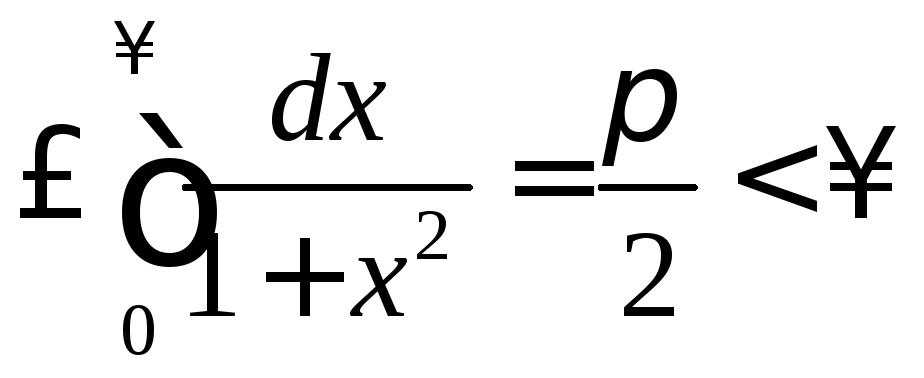 ).Значит,
).Значит,
![]() и заданный в условии интеграл расходится.
и заданный в условии интеграл расходится.
8.
Из уравнения следует, что 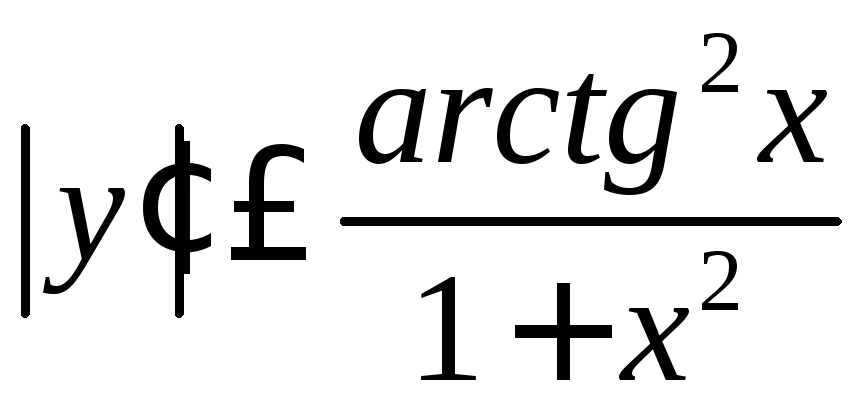 .
Для любых
.
Для любых ![]() ,
,
![]() имеем
имеем
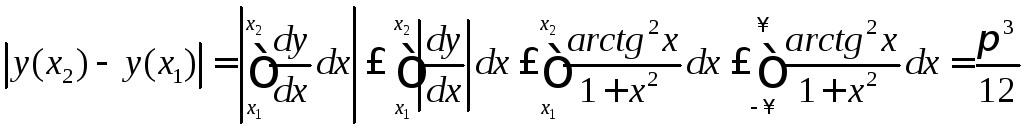
Отсюда
и следует ограниченность ![]() .
.
9.
От противного. Пусть
![]() ограничена, т.е. существуетС
такое, что
ограничена, т.е. существуетС
такое, что
![]() для всехn.
Построим для каждой точки
для всехn.
Построим для каждой точки
![]() окрестность
окрестность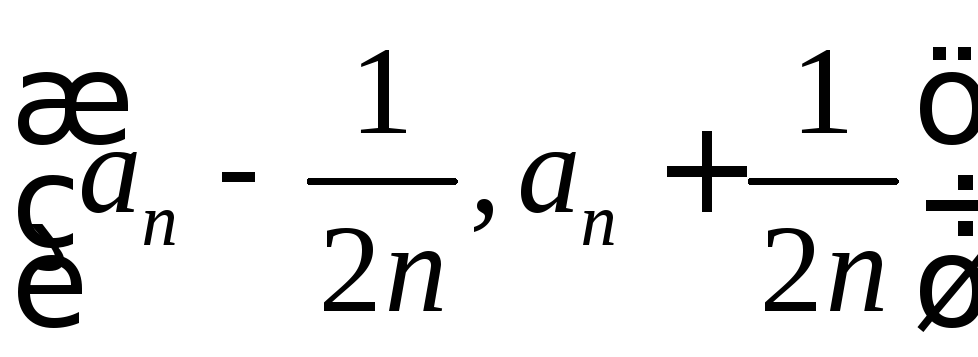 .
Из условия
.
Из условия![]() ,
,![]() следует, что эти окрестности не
пересекаются. Однако, в силу предположения,
все они находятся внутри интервала
следует, что эти окрестности не
пересекаются. Однако, в силу предположения,
все они находятся внутри интервала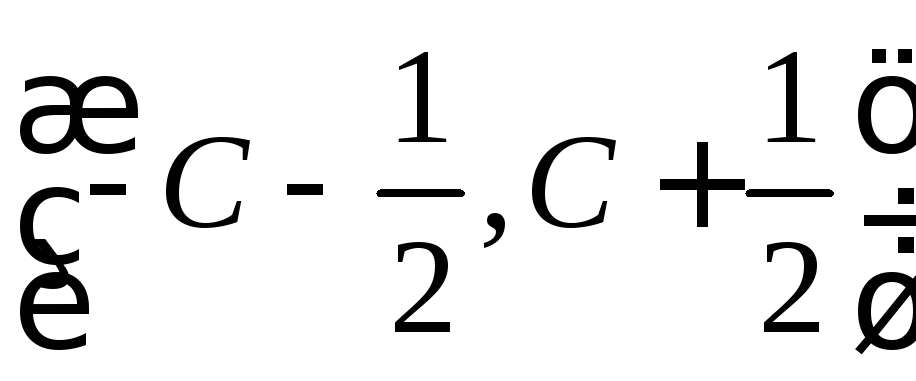 .
Поэтому сумма их длин не превосходит
.
Поэтому сумма их длин не превосходит![]() .
С другой стороны, если взять первыеN
членов последовательности, то сумма
длин соответствующих им интервалов
равна
.
С другой стороны, если взять первыеN
членов последовательности, то сумма
длин соответствующих им интервалов
равна
![]() .
Из-за расходимости гармонического ряда
эта сумма стремится к бесконечности
при
.
Из-за расходимости гармонического ряда
эта сумма стремится к бесконечности
при![]() .
Это противоречит полученному ранее
условию ограниченности суммы длин.
Значит,
.
Это противоречит полученному ранее
условию ограниченности суммы длин.
Значит,![]() не может быть ограниченной.
не может быть ограниченной.
10.
Пусть
 ,
где
,
где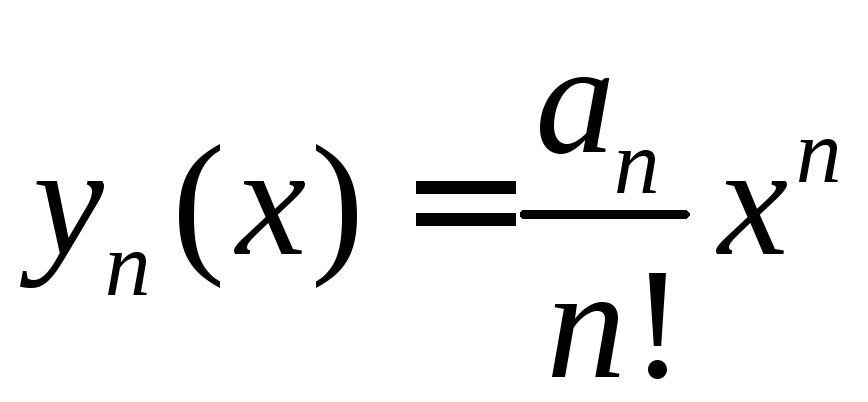 .Непосредственной проверкой убеждаемся,
что
.Непосредственной проверкой убеждаемся,
что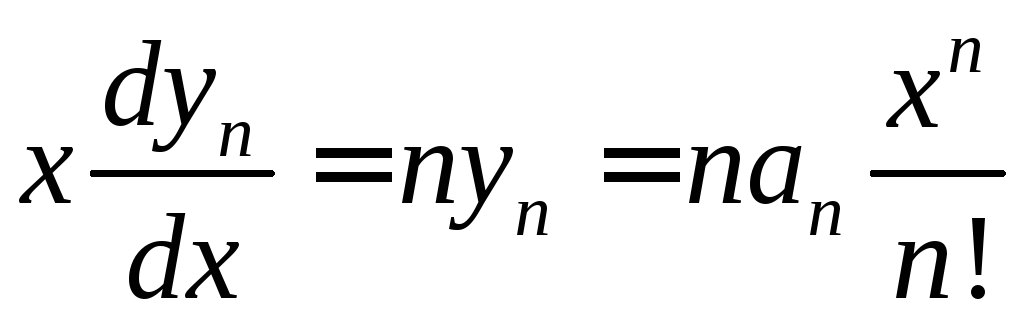 ,
,
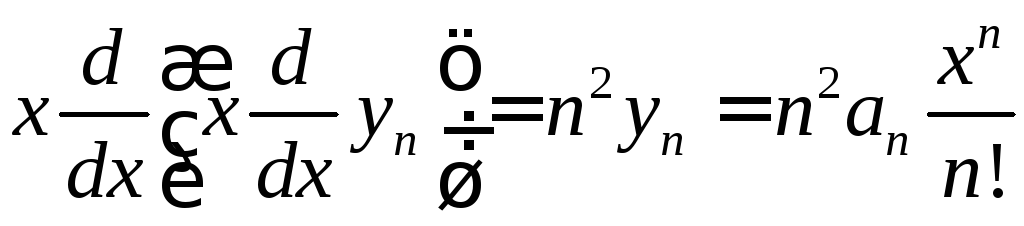 ,
,
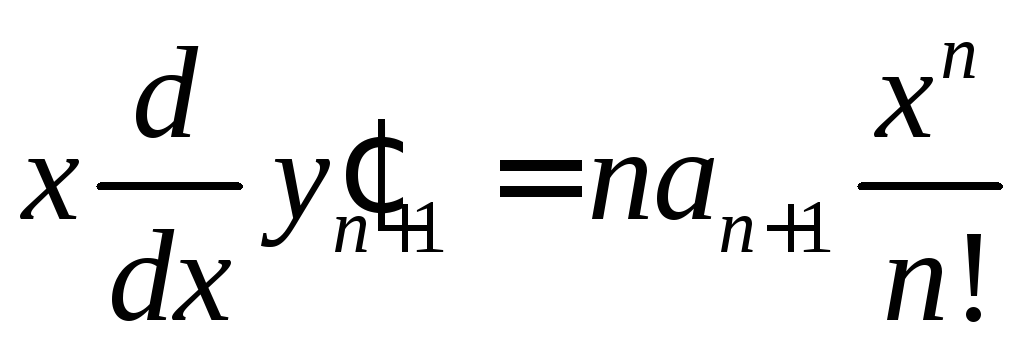 ,
,
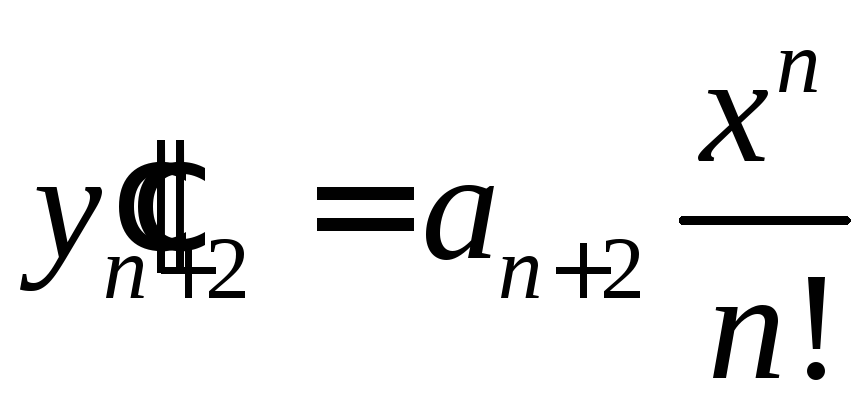 .
.
Рассмотрим выражение
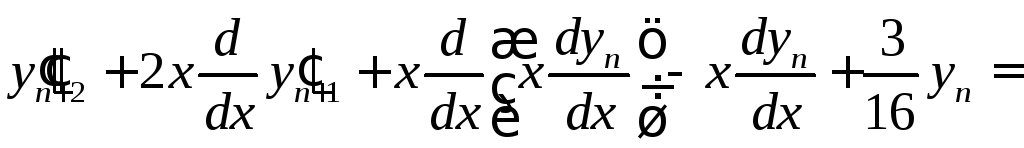 ,
,
 ,
,
![]() в
силу рекуррентного соотношения. Сложим
эти равенства для всех
в
силу рекуррентного соотношения. Сложим
эти равенства для всех![]() .
Получим
.
Получим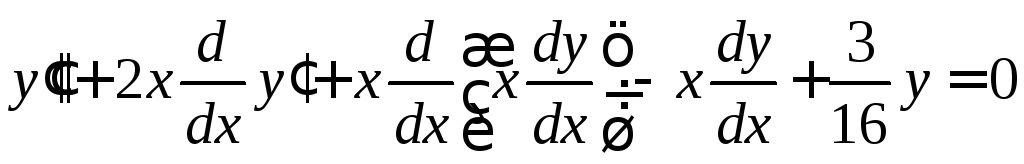 .
.
После
упрощения получим ![]() .
.
Простая
замена ![]() превращает это уравнение в уравнение
Эйлера
превращает это уравнение в уравнение
Эйлера ![]() .
Легко найти его частные решения вида
.
Легко найти его частные решения вида
![]() :
:
![]() ,
,
![]() ,
,
![]() или
или ![]() .
.
Общее
решение ![]() .
Из начальных условий (
.
Из начальных условий (![]() )
находим
)
находим ![]() и
и ![]() .
.
Ответ:
![]() .
.
Замечание. Решение уравнения Эйлера можно найти и стандартным способом, сведя его к уравнению с постоянными коэффициентами с помощью логарифмической замены переменной.
11.
Пусть ![]() - матрица
- матрица ![]() имеет все целые элементы, и ее обратная
имеет все целые элементы, и ее обратная
![]() также состоит из целых элементов. Тогда
также состоит из целых элементов. Тогда
![]() .
Тогда
.
Тогда ![]() или
или ![]() .
Введем
.
Введем ![]() .
.
![]() есть полином степени n
по t.
Полином
есть полином степени n
по t.
Полином ![]() принимает значения
1 или -1 в точках
принимает значения
1 или -1 в точках ![]() Значит,
Значит, ![]() принимает одно и тоже значение (1 или
-1) по крайне мере в (n+1)
точке. Но степень полинома равна n.
Поэтому полином постоянен:
принимает одно и тоже значение (1 или
-1) по крайне мере в (n+1)
точке. Но степень полинома равна n.
Поэтому полином постоянен: ![]() или
или ![]() .
Следовательно,
.
Следовательно, ![]() или
или ![]() .
Значит, матрица
.
Значит, матрица ![]() обратима. По формуле для элементов
обратной матрицы получаем, что они все
целые, т.к. определитель матрицы равен
1 или -1.
обратима. По формуле для элементов
обратной матрицы получаем, что они все
целые, т.к. определитель матрицы равен
1 или -1.
12.
Определим
последовательность функций
![]() следующим образом:
следующим образом:![]() ,
,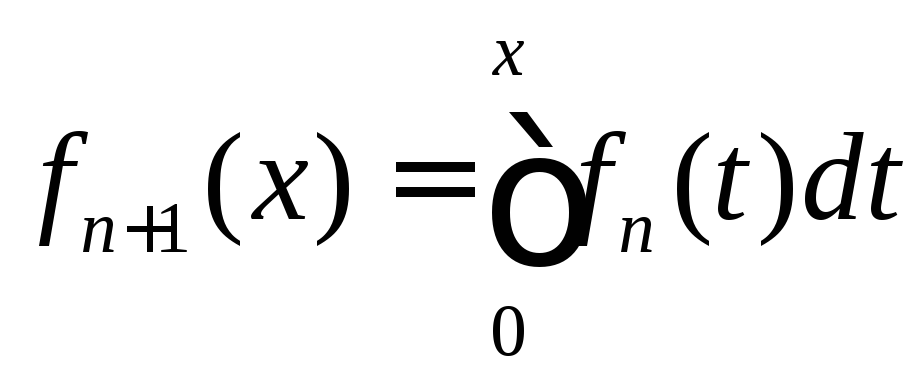 ,
,![]() .
Найдем представление для членов
последовательности.
.
Найдем представление для членов
последовательности.
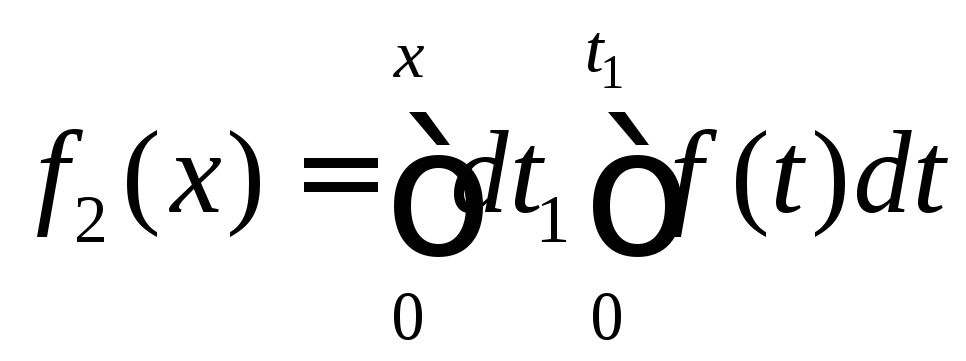 .
.
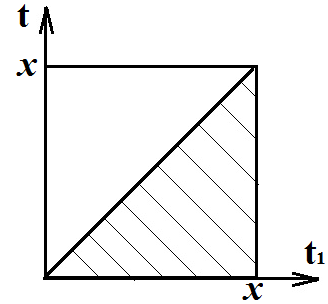 Поменяем
порядок интегрирования:
Поменяем
порядок интегрирования:
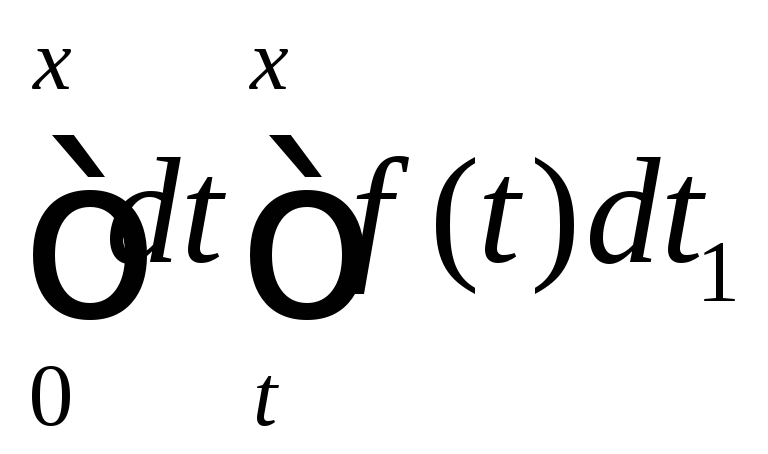 .
.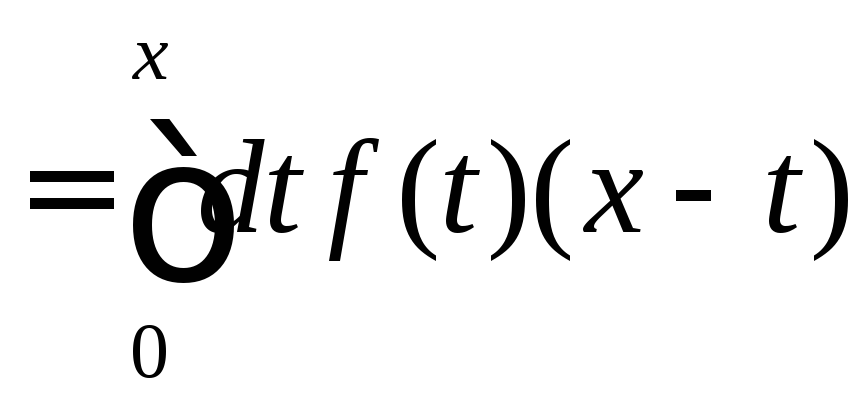 .
.![]() .
.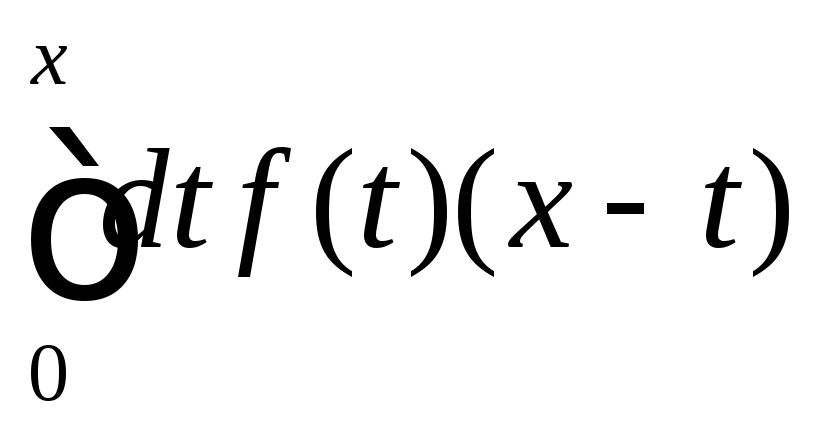 .
Аналогично,
.
Аналогично,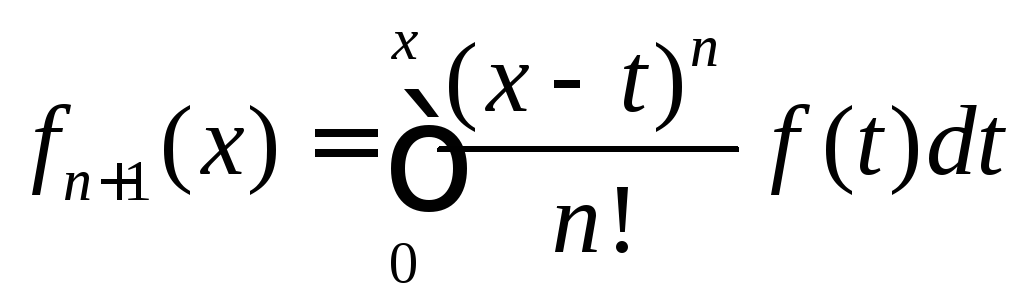 .
Докажем по индукции. База уже проверена.
Сделаем индукционный переход:
.
Докажем по индукции. База уже проверена.
Сделаем индукционный переход:
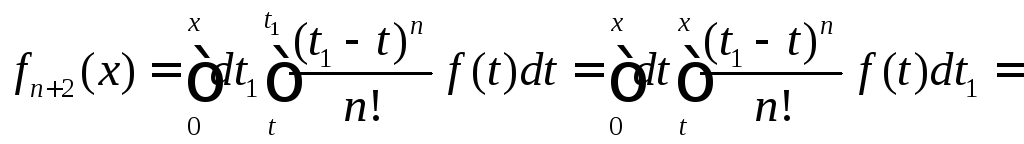
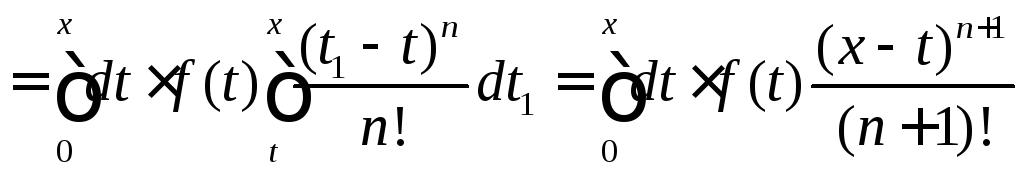 .Формула
доказана.
.Формула
доказана.
По
условию
![]() для всехn,
т.е.
для всехn,
т.е.
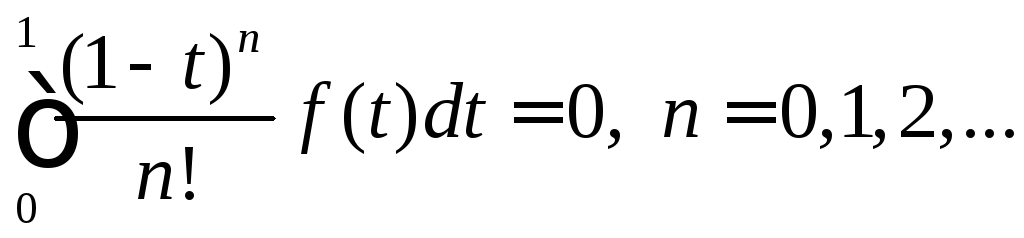
![]() -
есть полная система в
-
есть полная система в
![]() ,
а функцияf
ортогональна всем ее элементам. Значит,
,
а функцияf
ортогональна всем ее элементам. Значит,
![]() .
То есть
.
То есть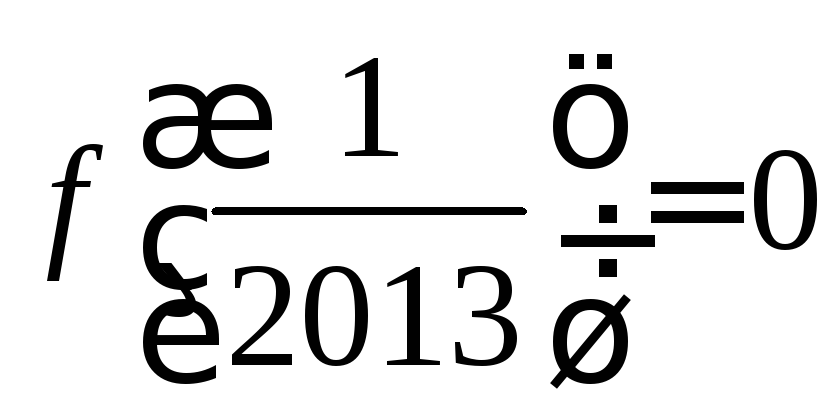 .
.
Количество участников, решивших задачи (определено по формуле: полная сумма набранных всеми участниками баллов за задачу, деленная на стоимость задачи).
|
№ задачи |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
Кол-во решивших |
26,2 |
51,9 |
31,3 |
41,2 |
10,5 |
12,6 |
10,3 |
18,6 |
14,5 |
5,9 |
3,4 |
4,8 |
