ЭЛЕКТРОТЕХНИКА ДОМАШНИЕ И КУРСОВЫЕ ЗАДАНИЯ

50

Методически е указания

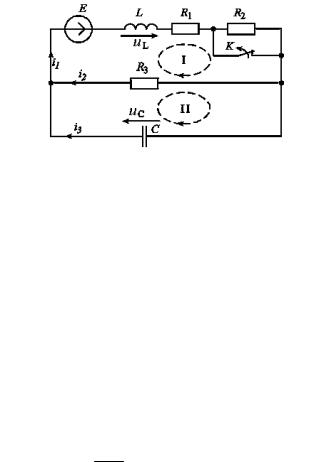
Рассмотрим порядок расчета переходных процессов на примере цепи варианта 30, схема которой представлена на рис. 6.2. Пара-

метры цепи: E = 104 В, R1 = 20 Ом, R2 = 100 Ом, R3 = 500 Ом, L = = 0,02 Гн, С = 0,5 мкФ.

Рис. 6.2

I.Расчет переходного процесса классическим методом

1. Построение математической модели электрической цепи.

Для послекоммутационной цепи составляем по законам Кирхгофа систему дифференциальных уравнений, дополненную (при необходимости) уравнениями связи:

ur = R ×ir , uL = L × diL / dt, iC = C × duC / dt.

Для рассматриваемой цепи с двумя узлами и тремя ветвями она содержит три уравнения по законам Кирхгофа и одно уравнение связи:

i1 - i2 - i3 = 0,
L	di1	+ (R + R	2	)i + R	3	i	2	= E,
	dt	1		1				(6.1)
- R3i2 + uC = 0,

i3 = C dudtC .

2. Составление дифференциального уравнения цепи.

Систему (6.1) путем последовательного исключения переменных сводим к одному дифференциальному уравнению второго порядка относительно переменной, удовлетворяющей законам коммутации (относительно тока iL или напряжения uC).

51

Для примера составим дифференциальное уравнение относительно uC. Из третьего и первого уравнений (6.1)

i2

=

uC

,

(6.2)

R3

i

= i

2

+ i

3

=

uC

+ C

duC

.

(6.3)

1

R3

dt

Дифференцируя (6.3) и подставляя результат во второе уравне-

ние (6.1), получим

d 2u

C

L + R C(R + R ) du

C

R + R + R

E

+

3 1

2

+

1 2 3

uC =

. (6.4)

LCR3

LC

dt2

dt

LCR3

Согласно классическому методу расчета, решение дифференциального уравнения (6.4) ищем в виде двух составляющих – прину-

жденной и свободной:
uC = uСпр + uСсв .	(6.5)

3. Определение начальных условий.

3.1. Независимые начальные условия, т.е. ток в катушке индуктивности i1(0+) и напряжение на конденсаторе uC(0+), определяем

	расчетом установившегося						процесса в докоммутационной цепи
	(резистор R2 закорочен):
	.i1 (0+ ) = i1 (0	− ) =			E		=104 /(20 + 500) = 0,2 A,
			R1		+ R3
							(6.6)
					E
	uC (0+ ) = uC	(0− ) =						× R3 =104 × 500 /(20 + 500) =100 В.
					R1 + R3

3.2. Зависимые начальные условия, т.е. значения остальных токов и напряжений на момент t = 0+, определяем из системы уравнений (6.1) при подстановке в нее независимых начальных условий:

i1 (0+ ) = i2 (0+ ) + i3 (0+ ),

L

di1

+ (R + R

2

) × i (0

+

) + R

3

× i

2

(0

+

) = E,

dt

t =0+

1

1

(6.7)

- R3 × i2 (0 + ) + uC (0+ ) = 0,

i3 (0+ ) = C

duC

.

dt

t =0+

52

Решение (6.7) дает:

i2 (0+ ) =

uC (0+ )

=

100

= 0,2 А,

R3

500

i3 (0+ ) = i1 (0+ ) - i2 (0+ ) = 0,2 - 0,2 = 0,

u

L

(0

+

) = L

di1

= E - (R + R

2

) × i (0

+

) - R × i

2

(0

+

) =

dt

t=0+

1

1

3

=104 - (20 +100) × 0,2 - 500 × 0,2 = -20 В,

di1

=

uL (0+ )

= -

20

= -1000 А/с,

dt

t=0+

L

0,02

duC

=

i3 (0+ )

= 0.

dt

t=0+

C

di1

duC

на момент времени t = 0+

Значения производных

и

dt

dt

необходимы для последующего определения постоянных интегрирования.

4. Определение принужденной составляющей.

В случае подключения цепи к источнику постоянной или синусоидальной ЭДС принужденный режим совпадает с установившимся режимом (при t → ∞).

Для послекоммутационной цепи после окончания переходного

процесса (см. рис. 6.2)
uСпр =		E		× R3 =	104 × 500	= 83,87 В. (6.8)
	R1	+ R2			20 +100 + 500
			+ R3

Такой же результат получается из уравнения (6.4), если учесть,

	что при постоянной ЭДС			d 2uCпр
	uCпр = const,	duCпр	= 0 ,		= 0 .
		dt		dt2

5. Определение свободной составляющей.

Свободная составляющая является решением однородного дифференциального уравнения, которое для рассматриваемого

примера имеет вид

d 2u

C

L + R C(R + R

2

) du

C

R + R + R

+

3 1

+

1 2 3

uC = 0 . (6.9)

dt 2

LCR3

dt

LCR3

53

2LCR3

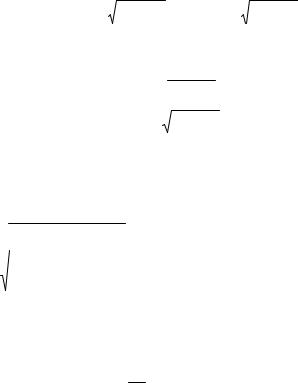
Запись свободной составляющей определяется видом корней характеристического уравнения: при вещественных корнях

u	Cсв	= A e p1t + A e p2t		(6.10)
		1	2

при комплексно-сопряженных

uCсв = A × e−δt sin(wt + y) ,

(6.11)

где p1,2 – корни характеристического уравнения; А1, А2, А, ψ – постоянные интегрирования.

5.1. Определение корней характеристического уравнения.

Характеристическое уравнение, соответствующее дифференциальному уравнению (6.4), имеет вид

p2 + 2dp + w02 = 0 .

(6.12)

При δ > ω0 его корни будут вещественными отрицательными:

p = -d +	d2 - w2	, p	2	= -d -	d2 - w2	,	(6.13)
1	0				0

а переходный процесс – апериодическим.

При δ < ω0 корни уравнения комплексно-сопряженные с отрицательной вещественной частью:

p1 = -d + j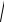w20 - d2 = -d + jw,

p2 = -d - j w02 - d2 = -d - jw,

(6.14)

а переходный процесс – колебательный. В последнем случае δ называют коэффициентом затухания переходного процесса, а ω – частотой свободных колебаний.

Для цепи рис. 6.2, согласно уравнению (6.4), d = L + R3C × (R1 + R2 ) = 5000 c−1 ,

w0	=		R1 + R2 + R3		=11135 c−1 .
			LCR3
	Корни характеристического уравнения
			p1,2 = (–5000 ± j 9950) с-1			(6.15)

комплексно-сопряжённые, переходный процесс колебательный, время переходного процесса tпп = 3t = 3/d = 0,6×10–3 с, период сво-

бодных колебаний Tсв = 2wp = 0,6312 ×10−3 c соизмерим со време-

нем переходного процесса.

54

5.2. Определение постоянных интегрирования.

Для определения постоянных интегрирования используем начальные условия: значения искомой переменной и ее производной в момент коммутации t = 0, полученные в п.3.

Случай вещественных корней. Общее решение для напряжения uC (t)

u	C		(t) = u		Cпр	+ A e p1t + A e p2t ,			(6.16)
						1		2
а для его производной:
		duC		= p A e p1t + p			2	A ep2t .	(6.17)
			dt		1	1		2

Уравнения (6.16) и (6.17) для момента времени t = 0 образуют систему для определения постоянных интегрирования А1, А2:

		uC (0) = uCпр + A1 + A2 ,
			duC		= A1 p1 + A2 p2 .	(6.18)
			dt
					t=0
Случай комплексно-сопряженных корней.
Общие решения для напряжения uC (t) и его производной:
		uC (t) = uCпр + Ae−δt sin(wt + y) ,				(6.19)
	duC	= -Ad ×e−δt sin(wt + y) + Aw×e−δt cos(wt + y) .				(6.20)
	dt

Уравнения (6.19) и (6.20) для момента времени t = 0 образуют систему уравнений для определения постоянных интегрирования

А, ψ:

uC (0) = uCпр + Asin y,
duC		= -Adsin y + Awcos y.	(6.21)
dt
		t=0

Для рассматриваемого примера (см. рис. 6.2) система уравне-

ний (6.21) имеет вид
	R3		E =		R3				E + Asin y,
	R + R	3		R + R		2	+ R	3
1			1

0 = -d × Asin y + w× Acos y.

55

Решение уравнений дает y = arctg(w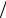d) = 63,3o ,

	A =	ER3	×(		1	-		1		) =18,05 В.
		sin y		R	+ R		R + R + R
				1	3		1	2	3

6. Получение решений для всех физических переменных цепи.

Решение для напряжения на конденсаторе получим подстановкой найденных значений принужденной и свободной составляющих в общее выражение (6.5):

uC (t) = 83,87 +18,05e−5000t sin(9950t + 63,3o ) .

Правильность решения проверяют на соответствие граничным условиям:

при t = 0 uC(0) = 83,87+18,05 sin 63,3o = 100 В;

при t → ∞ uC(∞) = 83,87 = uCпр.

Напряжения на остальных элементах цепи и токи i1, i2, i3 определяем из исходной системы (6.1) после подстановки в нее найденного решения для uC(t):

i3 (t) = C

duC

= 5 ×10

−7

e

−5000t

×18,05 ×[-5000

× sin(9950t + 63,3

o

) +

dt

+ 9950 × cos(9950t + 63,3o )] =

= e−5000t

×[0,045 × sin(9950t -116,7o ) + 0,09 × sin(9950 +153,3o )] =

= -0,1006 × e−5000t sin 9950t, A;

i2

(t) =

uC

= 0,1677 + 0,0361× e

−5000t

sin(9950t +

63,3

o

), A;

R3

i1 (t) = i2 + i3 = 0,1677 + e−5000t [0,0361sin(9950t + 63,3o ) -

- 0,1006sin 9950t)] = 0,1677 + 0,09035 × e−5000t sin(9950t +159o ), A; uL (t) = L didt1 = 0,02×0,09035×e−5000t [-5000sin(9950t +159o ) =

=+9950cos(9950t +159o )] =

=1,807×e−5000t [5sin(9950t - 21o ) + 9,95sin(9950t -111o )] =

=20,12×e−5000t sin(9950t -84o ),B;

56

uR1 (t) = i1R1 = 3,354 +1,807 × e−5000t sin(9950t +159o ), B; uR2 (t) = i1R2 =16,77 + 9,035 × e−5000t sin(9950t +159o ), B .

Пр им е ч а ние . При операциях с синусоидальными функциями рекомендуется использовать комплексный метод с последующим переходом к оригиналу.

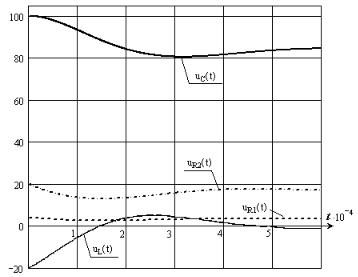
На рис. 6.3 приведены графики напряжений uC (t),uL (t),uR1 (t),uR2 (t). Для момента времени t = 2·10-4 с проверено выполнение II закона Кирхгофа:

uL + uR1 + uR2 + uC = E :3,7 + 2,69 + 13,45 + 84,18 = 104,02.

Графики токов i1 (t) , i2 (t) , i3 (t) приведены на рис. 6.4. Проверка выполнения первого закона Кирхгофа i1 − i2 − i3 = 0 для то-

го же момента времени t = 2·10-4 с дает: 0,135–0,169 +0,034=0.

Рис. 6.3

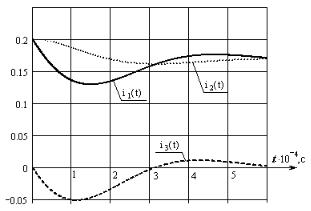
При колебательном переходном процессе (корни характеристического уравнения комплексные) графики строят для промежутка времени t = 1,5×T , где T = 2p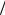w – период колебаний. При апериодическом процессе (корни характеристического уравнения веще-

ственные) этот промежуток составляет: 3tmax =			1			, где τ max –
			pmin

57

наибольшая постоянная времени, полученная при расчете свободной составляющей.

Рис. 6.4

В указанных промежутках должны быть рассчитаны не менее 15 точек для колебательного процесса и не менее 10 для апериодического процесса.

II.Расчет переходного процесса операторным методом

1. Строим операторную схему замещения послекоммутационной цепи. Для этого необходимо:

−мгновенные значения токов, напряжений и ЭДС заменить их изображениями по Лапласу;

−катушку индуктивности заменить последовательным соединением операторного сопротивления pL и добавочного источ-

ника, ЭДС которого совпадает по направлению с током iL (0− ) и равна L ×i(0− ) ;

− конденсатор заменить последовательным соединением операторного сопротивления 1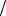 pC и добавочного источника, ЭДС которого направлена противоположно напряжению uC (0− ) и рав-

на uC (0− ) / p .

Операторная схема для рассматриваемой цепи изображена на рис. 6.5.

58

Рис. 6.5

2. Для полученной схемы замещения составляем систему уравнений по первому и второму законам Кирхгофа в операторной форме. Для рассматриваемого примера она имеет вид

I1 ( p) − I 2 ( p) − I3 ( p) = 0,

( pL + R1 + R2 )I1 ( p) + R3 I2 ( p) = Ep + Li1 (0),

(6.22)

pC1 I3 ( p) - R3 I2 ( p) = - uCp(0) ,

I3 ( p) = C ×[ pUC ( p) - uC (0)].

3. Решаем систему уравнений относительно изображения по Лапласу искомой переменной (в рассматриваемом случае относи-

тельно UC ( p) ). Решение должно быть представлено в виде отношения двух полиномов оператора p:

= G( p) UC ( p) H ( p) .

При этом необходимо добиться того, чтобы в составе Н(р) множитель при р в наивысшей степени был равен единице, как это требуется при разложении дроби на простейшие:

p2u

C

(0) + é

R1 + R2

× u

C

(0) +

1

× i (0)ù p +

1

E

ê

L

C

1

ú

LC

UC ( p) =

ë

û

.

é

2

æ

R + R

2

1

ö

R + R

2

+

R

3

ù

ç

1

÷

1

pê p

+ ç

+

÷ p +

ú

L

R3 LC

ê

è

R3C ø

ú

ë

û

После подстановки численных значений параметров и начальных условий получим

59