Лекция 04 Ряды

Лекция № 4

Ряд Тейлора, Маклорена. Основные разложения.

Вычисление пределов с использованием рядов

Рассмотрим степенной ряд (2) и пусть в интервале сходимости ряда сумма его равна некоторой функции т.е. :

(1)

Так как степенной ряд можно почленно дифференцировать во всём интервале сходимости (причём он также будет сходящимся в этом же интервале сходимости и сумма его равна производной от суммы исходного ряда), то продифференцируем его:

, где – есть сумма ряда.

Дифференцируем исходный ряд “” раз (причём на каждом этапе вновь будем иметь степенной ряд), в результате получим:

............................................................................................................

Если будем вычислять значения полученных рядов в , получим:

, , , и т. д.

и т.д.

Итак, зная, что бесконечно дифференцируемая функция является суммой степенного ряда (2), то коэффициенты этого ряда можно определить с помощью следующих формул Маклорена:

, , , , и т.д.

, ... и т.д.

И в результате получим ряд Маклорена:

Аналогично получаются формулы Тейлора:

, , , , ..., , ...

При этом ряд будет иметь следующий вид:

Замечание: Не всякая функция может быть представлена в виде суммы некоторого степенного ряда. Может оказаться:

• либо сумма полученного ряда не совпадает с исходной функцией;

• либо полученный ряд не имеет конечной суммы.

Определим условия разложимости функции в ряд Тейлора (Маклорена).

Рассмотрим ряд:

(1)

Обозначим через – “”–ную частичную сумму данного ряда (1), тогда можно записать: , где – есть “” – ный остаток ряда.

Сходимость ряда (1) к функции в означает, что:

или .

Теорема 1: Если функция имеет на интервале производную любого порядка, ограниченную одним и тем же числом , т.е. :

, то остаток ряда Тейлора стремится к нулю при , т.е. .

Доказательство:

Теорема о представлении функции в виде формулы Тейлора (см. предыдущий семестр) гласит: если функция раз дифференцируема в некоторой окрестности , тогда такая что:

где – остаточный член в форме Лагранжа.

Итак, рассматривая остаток ряда Тейлора в виде остаточного члена в форме Лагранжа будем иметь:

, но при правая часть последнего неравенства при любых конечных значениях .

Покажем справедливость последнего утверждения. Для чего рассмотрим следующий ряд: . Рассмотрим ,

т.е. данный ряд сходится для любых вещественных значениях . Но тогда по необходимому признаку сходимости ряда будем иметь:

для любого фиксированного значения . В нашем случае в качестве значения берётся значение .

Таким образом имеем, что при .

Итак, представление заданной функции в виде ряда Тейлора в окрестности состоит из двух этапов:

• Вычисление значений функции и её производных в и составление ряда Тейлора для функции . При этом полагается, что – бесконечное число раз дифференцируема.

• Определение интервала, в котором составленный ряд Тейлора сходится к заданной функции , т.е. устанавливается, для каких значений остаток ряда .

Основные разложения в ряд Маклорена

некоторых элементарных функций

1. Разложение показательной функции .

Для разложения функции в ряд Маклорена находим последовательно производные и вычисляем значение функции и её производных в точке .

, , , .... , , ,...

, , , ... , , , ...

По формуле Маклорена имеем:

, где , .

Кроме того, составим ряд Маклорена для функции :

.

Как нетрудно установить, полученный степенной ряд сходится на всей числовой оси:

, если – любое фиксированное число.

А тогда, по необходимому признаку сходимости ряда общий член ряда стремится к нулю при , т.е. , а тогда и , так как для всех фиксированных значений величина – есть величина конечная.

Итак, сумма такого ряда Маклорена есть сама функция, для которой этот ряд построен, т.е.

,

Если положить , то получим: .

2. Разложение синуса и косинуса.

Пусть . Тогда имеем:

, , , , , ....

, , , , , ... и т.д.

Поэтому ряд Маклорена для функции имеет вид:

.

Этот ряд действительно имеет своей суммой функцию при любом значении , так как остаточный член формулы Маклорена стремится к нулю при . В самом деле: , где – есть функция либо со знаком “+” или “–”, следовательно , но правая часть данного неравенства является общим членом сходящегося при любых значениях ряда Маклорена для функции , поэтому она (правая часть) стремится к нулю при для любых фиксированных . Т.е. . И тогда сумма полученного ряда равна самой функции: , .

Аналогично получаем:

, .

Из представления функций в виде рядов Маклорена видны характерные степени “” для чётной функции – чётные степени, для нечётной функции – нечётные степени.

Замечание. Последнее представление функции можно было бы получить из представления в виде ряда Маклорена для путём почленного дифференцирования.

Полученные разложения и удобны для вычисления приближённых значений и . Причём для малых значений достаточно взять немного членов разложения, чтобы достичь требуемую точность вычисления.

3. Биноминальный ряд.

Разложим в ряд Маклорена функцию: , где – любое действительное число. Получим значение функции и её производных:

, .

, .

, .

, .

............................................................................................

, .

...........................................................................................

Поэтому ряд Маклорена функции имеет вид:

Установим область сходимости данного ряда:

Если , то данный ряд будет сходящимся, т. е. Интервал сходимости данного ряда есть . Доказательство того факта, что остаточный член формулы Маклорена стремится к нулю здесь приводить не будем. Итак, имеем, что при верно равенство:

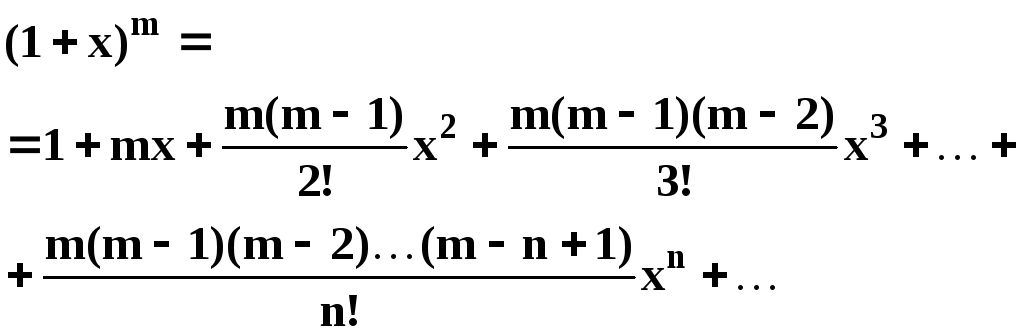
Если – целое положительное число, то ряд содержит всего слагаемых и превращается в формулу бинома Ньютона.

Рассмотрим ряд:

, т.к. это бесконечно убывающая геометрическая прогрессия при , со знаменателем .

С другой стороны: – это биноминальный ряд и он сходится к самой функции при .

При биноминальный ряд расходится.

Аналогично можно получить разложение функции в биноминальный ряд: ,

который имеет место при .

4. Логарифмическая функция .

Разложение данной функции в виде ряда Маклорена можно получить обычным способом, но намного эффективнее это выполнить основываясь на свойствах степенных рядов. А именно, зная, что степенной ряд можно интегрировать на любом отрезке из интервала сходимости ряда, можно получить:

, .

Область сходимости данного ряда , так как в точке получаем ряд Лейбница, который сходится. В левой же границе получаем гармонический ряд.

Аналогично получается разложение функции . Рассмотрим ряд:

при и .

Тогда:

Вычисление пределов с помощью рядов

Рассмотрим разложение функции в ряд Маклорена в окрестности точки :

. Данное представление можно рассматривать при малых значениях и следующим образом: и т.д., где обозначено, например, –функция, более высокого порядка малости, чем при . В действительности, отношение остатка ряда к будет стремиться к :

.

Этот факт будем использовать при представлении функции частью ряда, содержащего необходимое число слагаемых. Число удерживаемых слагаемых в ряде определяется величиной малости выражения, стоящего в знаменателе. Рассмотрим на примерах:

Пример 1. Вычислить значение предела:

. Здесь принято, что .

Пример 2. Вычислить значение предела:

.

Здесь и в дальнейшем используем следующий факт: .

Пример 3. Вычислить значение предела:

9