
Лекция 03 Ряды
.doc
Лекция № 3
Функциональные ряды: Область сходимости, правильно сходящиеся ряды, их свойства. Степенные ряды.
Область их сходимости.
Рассмотрим ряды, членами которого являются не числа, а некоторые функции:
![]() (1)
(1)
Ряды вида (1) называются функциональными.
Полагаем, что все функции
![]() –
определены и непрерывны в одном и том
же интервале (конечном или бесконечном).
–
определены и непрерывны в одном и том
же интервале (конечном или бесконечном).
Ряд
(1) может для одних значений “![]() ”
сходится, для других – расходится.
”
сходится, для других – расходится.
Значение
![]() ,
при котором числовой ряд
,
при котором числовой ряд
![]() сходится, называется точкой сходимости
функционального ряда (1).
сходится, называется точкой сходимости
функционального ряда (1).
Совокупность значений “![]() ”,
при которых ряд (1) сходится называется
областью
сходимости функционального ряда
(1).
”,
при которых ряд (1) сходится называется
областью
сходимости функционального ряда
(1).
Пример
1.
Рассмотрим ряд:
![]() Если
Если
![]() ,
то данный ряд–это бесконечно убывающая
геометрическая прогрессия, и она имеет
сумму, равную
,
то данный ряд–это бесконечно убывающая
геометрическая прогрессия, и она имеет
сумму, равную
![]() ,
где
,
где
![]() .
Для значений
.
Для значений
![]() данный ряд расходится. Отсюда следует,
что областью сходимости данного ряда
является интервал:
данный ряд расходится. Отсюда следует,
что областью сходимости данного ряда
является интервал:
![]() .
.
Сумма
функционального ряда также является
некоторой функцией, зависящей от “![]() ”:
”:
![]() .
.
Так
в примере
1:
![]() ,
причём эта сумма имеет смысл только при
,
причём эта сумма имеет смысл только при
![]() ,
т.е. в области сходимости данного
функционального ряда.
,
т.е. в области сходимости данного
функционального ряда.
По
аналогии числовых рядов введём понятие
“![]() ”–ной
частичной суммы ряда (1) и “
”–ной
частичной суммы ряда (1) и “![]() ”–
го остатка ряда соответственно:
”–
го остатка ряда соответственно:
![]() ,
,
![]() .
.
Если
для какого–то
![]() (из области сходимости ряда) ряд сходится,
то верны равенства:
(из области сходимости ряда) ряд сходится,
то верны равенства:
![]() и
и
![]() .
.
Известно, что сумма конечного числа слагаемых, каждое из которых есть непрерывная функция, есть функция непрерывная. Производная и интеграл от суммы конечного числа непрерывных функций также равна соответствующей сумме производных и интегралов от этих функций. Можно ли переносить указанные свойства на бесконечное число слагаемых? Можно, но не всегда!
Пример
2.
Рассмотрим ряд:
![]() .
.
Если
![]() , то
, то
![]() .
Если
.
Если
![]() ,
то ряд – убывающая геометрическая
прогрессия,
,
то ряд – убывающая геометрическая
прогрессия,
![]() и тогда:
и тогда:
![]() .
.
Таким
образом
![]() .
Т.е. функция
.
Т.е. функция
![]() – разрывная функция, хотя функции
– разрывная функция, хотя функции
![]() – функции непрерывные.
– функции непрерывные.
-
Функциональный ряд (1) называется правильно сходящимся (или мажорируемым) в области D , принадлежащей области сходимости ряда, если
 :
:
![]() ,
где ряд
,
где ряд
![]() – сходящийся ряд.
– сходящийся ряд.
Пример
3.
Рассмотрим ряд:
![]() . Этот ряд правильно сходится
. Этот ряд правильно сходится
![]() ,
так как
,
так как
![]() ,
а ряд
,
а ряд
![]() – сходится.
– сходится.
Свойства мажорируемых рядов.
(без доказательства)
Теорема
1:
Если ряд из непрерывных функций
мажорируем в области D
, то его сумма есть функция непрерывная
в этой области.
![]()
Теорема 2: Если ряд из непрерывных функций мажорируем, то этот ряд можно почленно интегрировать.
Пусть ряд сходится и имеет некоторую сумму в области D:
![]() ,
тогда:
,
тогда:
![]() , где
, где
![]() .
.
![]()
Теорема
3:
Если
ряд (1) , составленный из функций, имеющих
непрерывные производные, сходится в
области D
и его сумма
равна
![]() ,
а ряд, составленный из производных
,
а ряд, составленный из производных
![]() сходится в D
в правильно, то производная суммы ряда
сходится в D
в правильно, то производная суммы ряда
![]() равна сумме ряда из производных,
т.е.
равна сумме ряда из производных,
т.е.
![]() .
.
(Или:
Если ряд, составленный из производных
сходящегося ряда, мажорируем, то последний
можно почленно дифференцировать).
![]()
Пример 4. Рассмотрим ряд:
![]() .
Данный ряд мажорируемый и его сумма
есть непрерывная функция, но ряд,
составленный из производных:
.
Данный ряд мажорируемый и его сумма
есть непрерывная функция, но ряд,
составленный из производных:
![]() расходится,
т.к.
расходится,
т.к.
![]() .
.
Рассмотрим важнейший класс мажорируемых рядов, которые называются степенными рядами.
Степенные ряды. Интервал и область сходимости.
-
Степенным рядом называется функциональный ряд:
![]() ,
(1)
,
(1)
где
![]() – называются коэффициентами степенного
ряда. Если
– называются коэффициентами степенного
ряда. Если
![]() ,
то получим ряд по степеням “
,
то получим ряд по степеням “![]() ”:
”:
![]() ,
(2)
,
(2)
где
![]() – “
– “![]() ”
– ный член ряда,
”
– ный член ряда,
![]() –
нулевой член ряда.
–
нулевой член ряда.
Теорема
1:(Абеля)
Если степенной ряд (2) сходится в
![]() ,
то он сходится и притом абсолютно в
интервале:
,
то он сходится и притом абсолютно в
интервале:
![]() ,
т.е.
,
т.е.
![]() .
.
Доказательство:
Пусть
степенной ряд (2) сходится в
![]() , т.е. ряд
, т.е. ряд
![]() – сходится тогда
– сходится тогда
![]() ,
тогда
,
тогда
![]() такое, что
такое, что
![]() .
Перепишем ряд (2) в виде:
.
Перепишем ряд (2) в виде:
![]() и составим ряд, полученный из абсолютных
величин членов исходного ряда:
и составим ряд, полученный из абсолютных
величин членов исходного ряда:
![]() ,
,
причём:

![]()
![]() .
.
В
скобках стоит бесконечно убывающая
геометрическая прогрессия, если
![]() или
или
![]() .
Таким образом исходный ряд ограничен
сверху абсолютно сходящимся рядом.
Значит исходный ряд также сходится
абсолютно при
.
Таким образом исходный ряд ограничен
сверху абсолютно сходящимся рядом.
Значит исходный ряд также сходится
абсолютно при
![]() .
.
![]()
Следствие:
Если степенной ряд (2) расходится в
![]() ,
то он расходится и при всяком
,
то он расходится и при всяком
![]() .
.
Действительно,
пусть
![]() при котором он сходится, тогда по теореме
Абеля
при котором он сходится, тогда по теореме
Абеля
![]() ряд должен сходится, в том числе и в
ряд должен сходится, в том числе и в
![]() ,
что противоречит условию.
,
что противоречит условию.
![]()
Теорема Абеля позволяет определить интервал сходимости степенного ряда.
Вся
числовая ось может быть представлена
в виде множества точек, где степенной
ряд либо сходится, либо расходится (в
окрестности
![]() для ряда (2) или
для ряда (2) или
![]() для ряда (1)). Причём если границей
интервала сходимости является
для ряда (1)). Причём если границей
интервала сходимости является
![]() ,
то при
,
то при
![]() ряд сходится, а при
ряд сходится, а при
![]() ряд расходится. В граничных же точках
ряд может либо сходиться, либо расходиться.
ряд расходится. В граничных же точках
ряд может либо сходиться, либо расходиться.
-
Радиусом сходимости степенного ряда (2) называется такое число
 ,
что для всех
,
что для всех
 – степенной ряд сходится, а для всех
– степенной ряд сходится, а для всех
 ряд расходится.
ряд расходится. -
Интервал
 называется интервалом
сходимости степенного ряда (2).
Принимаем, что для рядов, расходящихся
при всех действительных чисел, кроме
называется интервалом
сходимости степенного ряда (2).
Принимаем, что для рядов, расходящихся
при всех действительных чисел, кроме
 ,
радиус сходимости
,
радиус сходимости
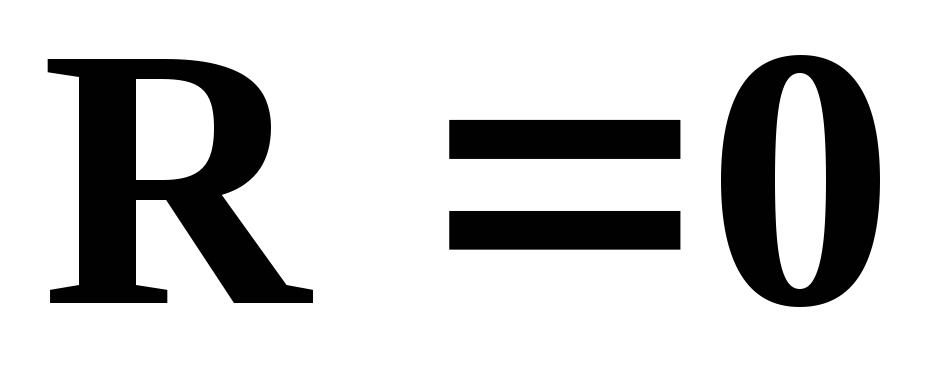 ,
а для рядов, сходящихся для всех
действительных чисел
,
а для рядов, сходящихся для всех
действительных чисел
 .
.
Для
степенных рядов (1) всё сказанное остаётся
в силе; центр интервала сходимости будет
находиться в
![]() ,
т.е. интервал
,
т.е. интервал
![]() является интервалом сходимости ряда.
является интервалом сходимости ряда.
Рассмотрим ряд, составленный из абсолютных величин членов ряда (2):
![]() . Данный ряд будет сходиться (т.к. он
знакоположительный и к нему применим,
например, признак Даламбера) если
. Данный ряд будет сходиться (т.к. он
знакоположительный и к нему применим,
например, признак Даламбера) если
![]() и расходиться, если
и расходиться, если
![]() ,
где
,
где
 .
Множество значений
.
Множество значений
![]() ,
при которых данный предел меньше 1 и
будет интервалом сходимости степенного
ряда.
,
при которых данный предел меньше 1 и
будет интервалом сходимости степенного
ряда.
Пример 5. Рассмотрим степенной ряд:
![]() .
.
Здесь:
![]() ,
,
![]() .
Рассмотрим:
.
Рассмотрим:
![]() .
.
На
основании признака Даламбера, получим:
при
![]() – ряд будет сходиться, а при
– ряд будет сходиться, а при
![]() – ряд будет расходиться. Для установления
области сходимости рассмотрим поведение
ряда в граничных точках:
– ряд будет расходиться. Для установления
области сходимости рассмотрим поведение
ряда в граничных точках:
Пусть
![]() :
тогда ряд будет числовым
:
тогда ряд будет числовым
![]() .
.
При
![]() имеем:
имеем:
![]() . Наряду с полученными знакочередующимися
числовыми рядами рассмотрим ряд:
. Наряду с полученными знакочередующимися
числовыми рядами рассмотрим ряд:
![]() – этот
ряд сходящийся и ограничивающий сверху
имеющиеся ряды. Последний ряд сходится.
Отсюда следует, что ряды в граничных
точках интервала также сходятся. Тогда
областью сходимости исходного ряда
будет область:
– этот
ряд сходящийся и ограничивающий сверху
имеющиеся ряды. Последний ряд сходится.
Отсюда следует, что ряды в граничных
точках интервала также сходятся. Тогда
областью сходимости исходного ряда
будет область:
![]() .
.
Пример 6. Найдём область сходимости ряда:
![]() .
.
Составим
отношение:
![]() .
.
Найдём
![]() .
.
Согласно
признаку Даламбера, ряд будет сходиться,
если
![]() ,
т.е.
,
т.е.
![]() .
Таким образом, интервалом сходимости
ряда является интервал:
.
Таким образом, интервалом сходимости
ряда является интервал:
![]() .
Для определения области сходимости
ряда рассмотрим поведение ряда в
граничных точках интервала:
.
Для определения области сходимости
ряда рассмотрим поведение ряда в
граничных точках интервала:
Пусть
![]() :
:
![]()
![]() – ряд
Лейбница, он сходится.
– ряд
Лейбница, он сходится.
Рассмотрим вторую границу:
![]() :
:
![]()
![]() – гармонический
ряд, он расходится. Таким образом,
областью сходимости данного ряда
является множество
– гармонический
ряд, он расходится. Таким образом,
областью сходимости данного ряда
является множество
![]() .
.
Операции над степенными рядами
Степенные ряды относятся к классу мажорируемых рядов в области их сходимости.
Теорема
1:
Степенной ряд (2) является рядом на
любом промежутке из интервала сходимости
ряда, т.е.
![]() , где
, где
![]() ,
,
![]() –
радиус сходимости ряда (2).
–
радиус сходимости ряда (2).
Доказательство:
Так
как
![]() ,
то при
,
то при
![]() ряд сходится, причём сходится абсолютно,
т.е.
ряд сходится, причём сходится абсолютно,
т.е.
![]() – сходится.
– сходится.
Но в рассматриваемом промежутке:
![]() ,
,
![]() ,
т.е. исходный ряд мажорируется сходящимся
рядом.
,
т.е. исходный ряд мажорируется сходящимся
рядом.
![]()
Следствие: Сумма степенного ряда есть функция непрерывная на любом отрезке из интервала сходимости.
Теорема
2:
Степенной ряд можно интегрировать на
любом отрезке из интервала сходимости.
![]()
Теорема
3:
Степенной ряд (2) можно дифференцировать
на всём интервале сходимости, т.е.
![]() ,
причём:
,
причём:
![]() При этом интервалы сходимости
исходного и полученного при дифференцировании
ряда совпадают.
При этом интервалы сходимости
исходного и полученного при дифференцировании
ряда совпадают.
Доказательство:
Рассмотрим
продифференцированный ряд:
![]() . Покажем, что он сходится также в
. Покажем, что он сходится также в
![]() .
Действительно, рассмотрим:
.
Действительно, рассмотрим:
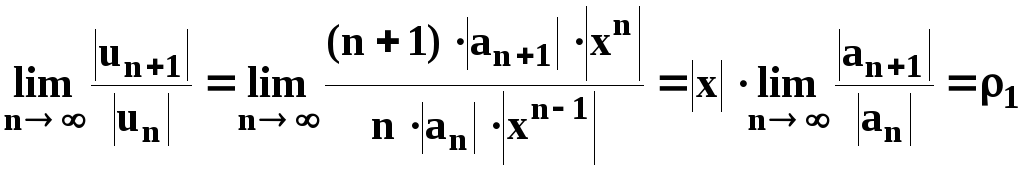
Для
исходного ряда:
 .
.
Итак,
![]() .
.
![]()
