- •Глава 8 элементы аналитической геометрии
- •§ 8.1. Прямые в аффинном пространстве
- •§ 8.2. Плоскости в аффинном пространстве
- •§ 8.3. Прямые и плоскости в аффинном пространстве
- •§ 8.4. Кривые второго порядка
- •Классификация кривых второго порядка, основанная на инвариантах
- •§ 8.5. Поверхности второго порядка
§ 8.2. Плоскости в аффинном пространстве
Пусть
в аффинном пространстве
![]() зафиксирована система координат
зафиксирована система координат![]() ,
заданы точка
,
заданы точка
![]() и система линейно независимых векторов
и система линейно независимых векторов![]() .
Тогда множество точек аффинного
пространства
.
Тогда множество точек аффинного
пространства![]() ,
радиусы-векторы
,
радиусы-векторы![]() которых удовлетворяют уравнению
которых удовлетворяют уравнению
![]() ,
(8.2.1)
,
(8.2.1)
где
![]() и
и![]() принимают любые значения из поля
принимают любые значения из поля![]() ,
называется
,
называется![]() -мерной
плоскостью
или, короче,
-мерной
плоскостью
или, короче,
![]() -плоскостью,
проходящей через точку
-плоскостью,
проходящей через точку
![]() параллельнонаправляющему
подпространству
параллельнонаправляющему
подпространству
![]() .
Соотношение (8.2.1) называется параметрическим
уравнением плоскости в векторной форме.
.
Соотношение (8.2.1) называется параметрическим
уравнением плоскости в векторной форме.
Прямые
можно рассматривать как одномерные
плоскости;
![]() -мерные
плоскости аффинного пространства
-мерные
плоскости аффинного пространства![]() называютсягиперплоскостями
(плоскостями).
называютсягиперплоскостями
(плоскостями).
Две плоскости, имеющие одну общую точку и одно и то же направляющее подпространство, совпадают. Параллельные плоскости не имеют общих точек, но их направляющие подпространства совпадают.
Пусть
в выбранной системе координат
![]() ,
,![]()
![]() ,
,![]() .
Тогда векторное уравнение (8.2.1) равносильно
.
Тогда векторное уравнение (8.2.1) равносильно![]() координатным уравнениям
координатным уравнениям
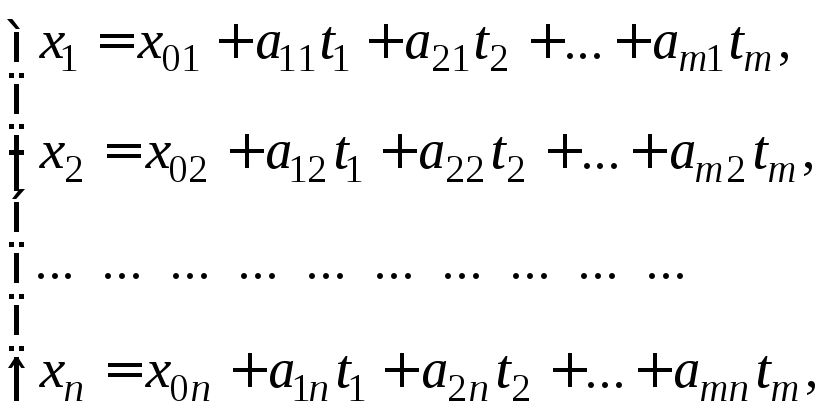 (8.2.2)
(8.2.2)
которые называются параметрическими уравнениями плоскости в координатной форме.
Если
в аффинном пространстве
![]() заданы точки
заданы точки![]() ,
,![]() ,
,![]()
![]()
![]() и
векторы
и
векторы![]()
![]()
![]()
![]()
![]() ,
линейно независимы, то через эти точки
можно провести единственную
,
линейно независимы, то через эти точки
можно провести единственную![]() -плоскость
с координатными уравнениями
-плоскость
с координатными уравнениями
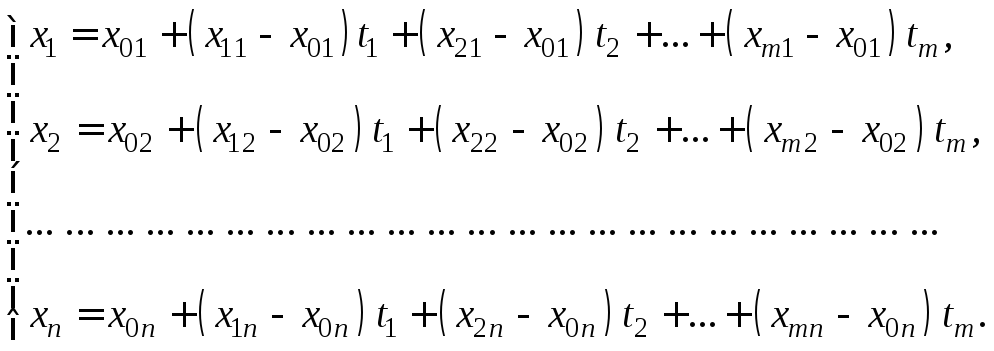 (8.2.3)
(8.2.3)
Вектор
![]() ,
ортогональный ко всемнаправляющим
векторам
,
ортогональный ко всемнаправляющим
векторам
![]() плоскости, заданной в виде (8.2.1), называетсявектором
нормали этой
плоскости.
Умножая скалярно обе части равенства
(8.2.1) на вектор нормали
плоскости, заданной в виде (8.2.1), называетсявектором
нормали этой
плоскости.
Умножая скалярно обе части равенства
(8.2.1) на вектор нормали
![]() ,
получаем с учетом обозначения
,
получаем с учетом обозначения![]() уравнение
уравнение
![]() ,
(8.2.4)
,
(8.2.4)
которое
называется векторным
уравнением плоскости,
проходящей
через точку
![]() с радиусом-вектором
с радиусом-вектором![]() перпендикулярно
вектору
перпендикулярно
вектору
![]() .
В случае прямоугольной системы координат
.
В случае прямоугольной системы координат![]() вместо векторного можно записать
следующеекоординатное
уравнение
плоскости,
проходящей через точку
вместо векторного можно записать
следующеекоординатное
уравнение
плоскости,
проходящей через точку
![]() перпендикулярно
вектору
перпендикулярно
вектору
![]()
![]() ,
(8.2.5)
,
(8.2.5)
которое еще называется общим уравнением плоскости.
Гиперплоскость,
проходящая через точку
![]()
![]() параллельно
подпространству
параллельно
подпространству![]() ,
порожденному линейно независимыми
векторами
,
порожденному линейно независимыми
векторами![]()
![]() ,
,![]()
![]() ,...,
,...,![]() ,
задается уравнением
,
задается уравнением
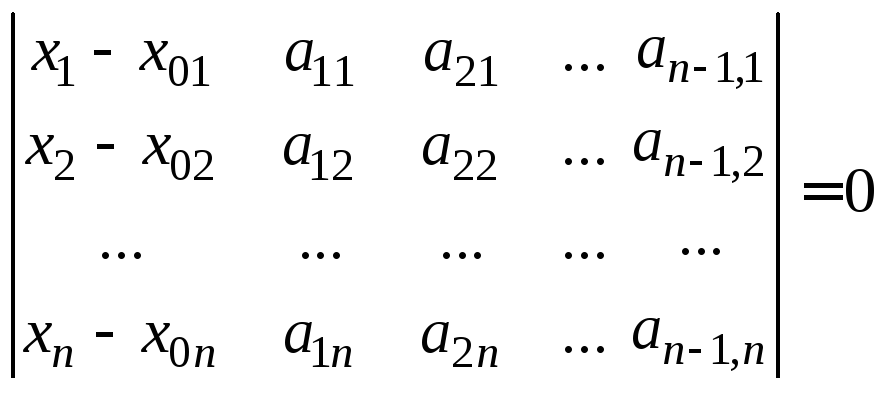 .
(8.2.6)
.
(8.2.6)
Гиперплоскость,
проходящая через
![]() точек
точек![]()
![]() ,
, ![]()
![]() , …,
, …,![]()
![]() ,
определяющих систему линейно независимых
векторов
,
определяющих систему линейно независимых
векторов
![]() ,
задается уравнением
,
задается уравнением
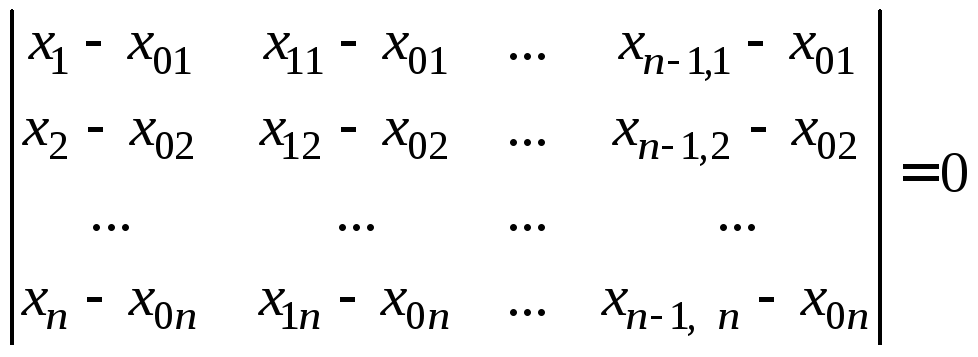 .
(8.2.7)
.
(8.2.7)
Необходимым
и достаточным условием того, что
![]() точка
точка![]() аффинного пространства
аффинного пространства![]() лежит на одной гиперплоскости, является
линейная зависимость векторов
лежит на одной гиперплоскости, является
линейная зависимость векторов![]() .
.
Угол
![]() между двумя плоскостями
с векторами нормалей
между двумя плоскостями
с векторами нормалей
![]() и
и![]() определяется как угол между двумя
векторами
определяется как угол между двумя
векторами![]() ,
,![]() ,
не превышающий
,
не превышающий![]() ,
и вычисляется по формуле
,
и вычисляется по формуле
![]() .
(8.2.8)
.
(8.2.8)
Расстояние
![]() от точки
от точки
![]() с радиусом-вектором
с радиусом-вектором![]() до плоскости,
заданной уравнением (8.2.4), определяется
как минимальное расстояние от точки
до плоскости,
заданной уравнением (8.2.4), определяется
как минимальное расстояние от точки
![]() до точек плоскости и вычисляется по
формуле
до точек плоскости и вычисляется по
формуле
![]() .
(8.2.9)
.
(8.2.9)
Расстояние
от точки
![]() до плоскости равно расстоянию от этой
точки до основания перпендикуляра,
опущенного из нее на плоскость.
до плоскости равно расстоянию от этой
точки до основания перпендикуляра,
опущенного из нее на плоскость.
Расстояние
![]() между двумя параллельными плоскостями
с уравнениями
между двумя параллельными плоскостями
с уравнениями
![]() равно расстоянию от некоторой точки
равно расстоянию от некоторой точки![]() ,
лежащей на второй плоскости, до первой
плоскости и вычисляется по формуле
,
лежащей на второй плоскости, до первой
плоскости и вычисляется по формуле
![]() .
(8.2.10)
.
(8.2.10)
Пример
1. Составьте
общее уравнение плоскости, параллельной
плоскости
![]() и отстоящей от точки
и отстоящей от точки![]() на расстояние
на расстояние![]() .
.
Решение.
В силу того, что векторы нормалей у
параллельных плоскостей коллинеарны,
можно записать общее уравнение искомой
плоскости:
![]() .
Для нахождения
.
Для нахождения![]() воспользуемся соотношением (8.2.9), в
котором
воспользуемся соотношением (8.2.9), в
котором![]()
![]()
![]() .
Получим:
.
Получим:
![]() ,
,
откуда
![]() и
и![]() либо
либо![]() .
Следовательно, существуют две плоскости
с общими уравнениями
.
Следовательно, существуют две плоскости
с общими уравнениями![]() и
и![]() ,
удовлетворяющими условию данной задачи.
,
удовлетворяющими условию данной задачи.
Пример
2. Составьте
параметрическое уравнение плоскости,
проходящей через точку
![]() параллельно плоскости
параллельно плоскости![]() .
.
Решение.
Считая систему координат ортогональной,
найдем направляющие векторы
![]() искомой плоскости из условия
искомой плоскости из условия![]() ,
где
,
где![]() .
Пусть
.
Пусть![]() .Тогда
.Тогда
![]() .
Отсюда
.
Отсюда
![]() .
Выбирая последовательно для
.
Выбирая последовательно для![]() ,
а для
,
а для![]() ,
получаем
,
получаем![]()
![]() ,
что позволяет записать на основании
равенств (8.2.2) следующее параметрическое
уравнение искомой плоскости:
,
что позволяет записать на основании
равенств (8.2.2) следующее параметрическое
уравнение искомой плоскости:
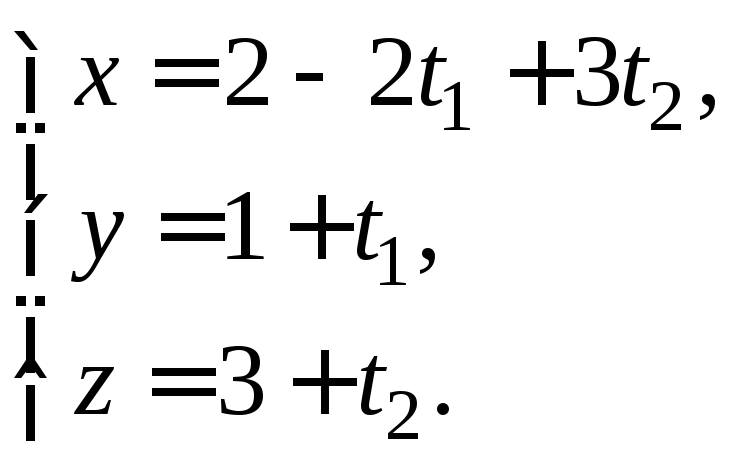
Пример
3. Вычислите
расстояние от точки
![]() до плоскости, проходящей через точки
до плоскости, проходящей через точки![]()
![]() .
.
Решение.
Считая, что координаты всех точек заданы
в прямоугольной системе координат,
запишем общее уравнение плоскости
![]() ,
для чего воспользуемся соотношением
(8.2.7):
,
для чего воспользуемся соотношением
(8.2.7):
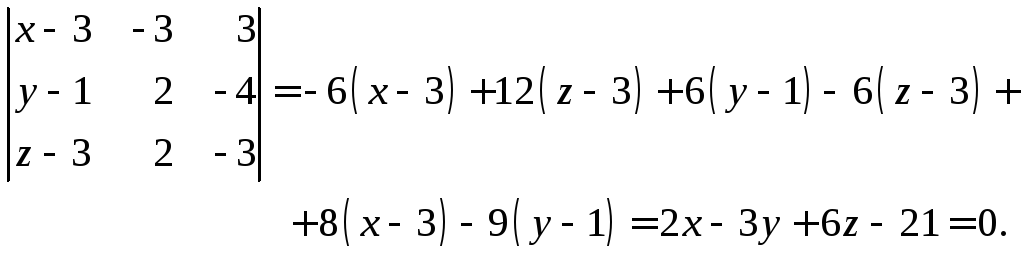
Искомое
расстояние вычислим по формуле (8.2.9), в
которой
![]() ,
,![]() и
и![]() .
Получим:
.
Получим:
![]() .
.
Пример 4. Найдите параметрическое уравнение плоскости, заданной системой линейных алгебраических уравнений:
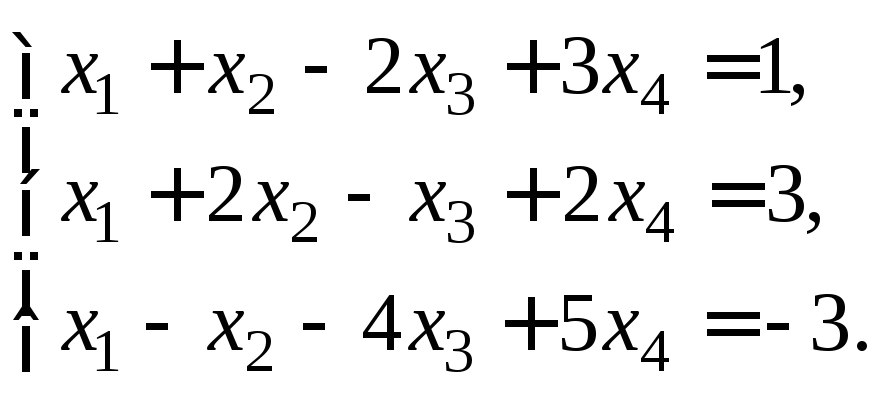
Решение.
Запишем систему уравнений в матричном
виде и найдем ее общее решение
![]() методом Гаусса.
методом Гаусса.
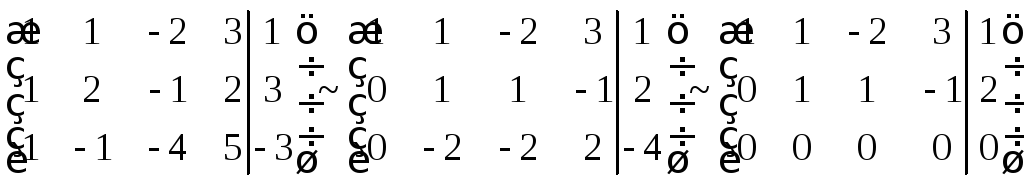 .
.
Выберем
в качестве свободных переменных
переменные
![]() и
и![]() .
Тогда
.
Тогда
![]() ,
,
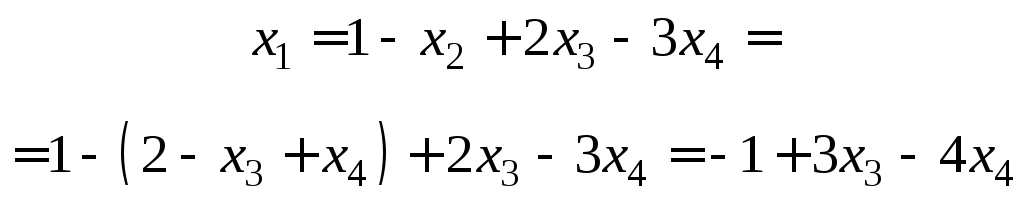
и
![]() .
.
Представляя
общее решение
![]() неоднородной системы в виде суммы
частного решения этой системы и общего
решения соответствующей однородной
системы, получаем разложение
неоднородной системы в виде суммы
частного решения этой системы и общего
решения соответствующей однородной
системы, получаем разложение
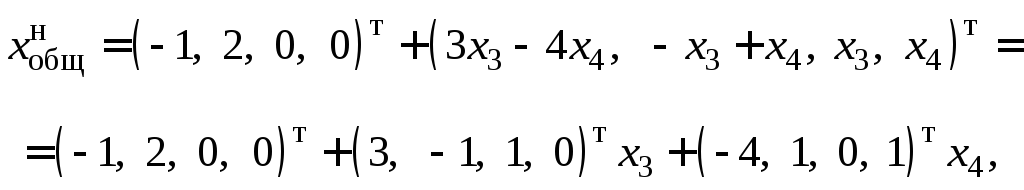
представляющее
искомое параметрическое уравнение
плоскости
![]() ,
в котором
,
в котором![]() ,
,![]() и
и![]() .
.
Таким
образом, множество решений неоднородной
системы линейных уравнений можно
рассматривать как
![]() -плоскость
в аффинном пространстве
-плоскость
в аффинном пространстве![]() .
.
В задачах, требующих вычисления скалярных произведений, предполагается, что система координат прямоугольная.
8.2.1.
Составьте общее уравнение плоскости,
проходящей через точку
![]() перпендикулярно вектору
перпендикулярно вектору![]() .
.
8.2.2.
Составьте общее уравнение плоскости,
проходящей через точку
![]() параллельно двум векторам
параллельно двум векторам
![]() и
и![]() .
.
8.2.3.
Составьте общее уравнение плоскости,
проходящей через точки
![]() и
и![]() параллельно вектору
параллельно вектору![]() .
.
8.2.4.
Составьте общее уравнение плоскости,
проходящей через три точки
![]() ,
,![]() ,
,![]() .
.
8.2.5. Составьте параметрическое уравнение плоскости:
а) проходящей
через точку
![]() параллельно векто-рам
параллельно векто-рам
![]() и
и![]() ;
;
б) проходящей
через точки
![]() ,
,![]() па-
раллельно
вектору
па-
раллельно
вектору![]() ;
;
в)
заданной общим уравнением
![]() .
.
8.2.6. Определите взаимное расположение плоскостей:
а)
![]()
б)
![]()
в)
![]() .
.
8.2.7. Найдите координаты точек пересечения плоскости
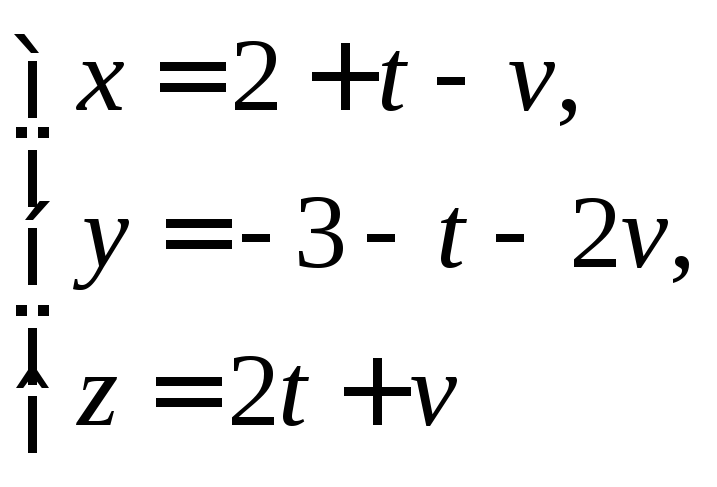
с осями координат.
8.2.8. Напишите общее уравнение плоскости

8.2.9.
Составьте уравнение плоскости, проходящей
через точку
![]() перпендикулярно двум плоскостям
перпендикулярно двум плоскостям
![]() и
и![]() .
.
8.2.10.
Найдите точку, симметричную точке
![]() относительно плоскости
относительно плоскости![]() .
.
8.2.11.
Составьте уравнения плоскостей,
проходящих через точку
![]() параллельно координатным плоскостям.
параллельно координатным плоскостям.
8.2.12.
Напишите параметрическое уравнение
плоскости
![]() .
.
8.2.13. Найдите параметрическое уравнение плоскости, заданной системой линейных алгебраических уравнений:

8.2.14.
В аффинном пространстве
![]() дана плоскость
дана плоскость![]() ,
где
,
где![]()
![]() .
Установите, принадлежат ли этой плоскости
векторы
.
Установите, принадлежат ли этой плоскости
векторы![]() и
и![]() .
.
8.2.15. При
каких
![]() плоскости
плоскости![]() и
и![]() :
:
а) пересекаются;
б) параллельны;
в) совпадают?
8.2.16. Найдите
расстояние от точки
![]() до плоскости:
до плоскости:
а)
![]() ;
;
б)
![]() ;
;
в)
![]() ;
;
г)
![]() .
.
8.2.17. Найдите расстояние между параллельными плоскостями:
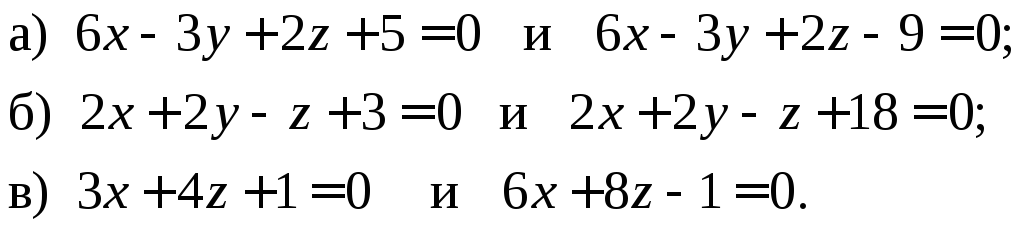
8.2.18.
а)
Составьте уравнения плоскостей,
параллельных плоскости
![]() и отстоящих от нее на расстояние 3.
и отстоящих от нее на расстояние 3.
б) Составьте уравнения плоскостей, параллельных плоскости
![]() и
отстоящих от нее на расстояние 3.
и
отстоящих от нее на расстояние 3.
в) Составьте уравнения плоскостей, параллельных плоскости
![]() и
отстоящих от точки
и
отстоящих от точки
![]() на расстояние 3.
на расстояние 3.
г)
Составьте уравнения плоскостей,
параллельных плоскости
![]() и отстоящих от начала координат на
расстояние 3.
и отстоящих от начала координат на
расстояние 3.
8.2.19. Найдите угол между плоскостями: