§ 74. Отыскание двусвязных компонент

В этом параграфе мы рассмотрим применение поиска в глубину к выделению 2-связных компонент графа. Здесь дело обстоит не так просто, как в предыдущей за­даче. Конечно, можно было бы, удаляя поочередно вер­шины графа и каждый раз выделяя связные компоненты, найти его точки сочленения и блоки. Такой подход, од­нако, приводит к алгоритму сложности по крайней мере O(|EG|*|G|)Использование более глубоких свойств ПГ позволяет получить линейный по сложности алгоритм решения этой задачи.

В дальнейшем удобно использовать следующие терми­ны. Пусть D=(V, А)—ориентированное дерево, х, у € V. Назовем х отцом вершины у, а у — сыном верши­ны х, если дуга (х, у) принадлежит А. Будем говорить, что вершины хиу сравнимы, если одна из них достижи­ма из другой. Если при этом у достижима из х, то х — предок вершины у, а у — потомок вершины х. Подграф графа D, порожденный множеством, состоящим из верши­ны у и всех ее потомков, будем обозначать через D_v и называть поддеревом с корнем у.

Пусть в графе G проделан поиск в глубину из верши­ны v₀ и получены остовное глубинное дерево Т и множе­ство обратных ребер В.

Следующие три утверждения дают теоретическую ос­нову для разработки эффективного алгоритма выделения двусвязных компонент.

Утверждение 74.1. Если дуга (х, у) принадле­жит В, то х является потомком вершины у в Т.

Надо доказать, что вершина х принадлежит подде­реву Т_у. Предположим противное. Согласно утверждению 73.2 вершина х получает свой ПГ-номер позже, чем у. Поэтому присвоение вершине х ПГ-номера произойдет не раньше, чем будут посещены все вершины дерева Т_у и произойдет возвращение в вершину s = F(y). Но возвра­щение в s не может произойти прежде, чем все вершины множества N_y получат ПГ-номера. Поскольку х € N_y и ПГ-номера к этому моменту не имеет, то получаем противоречие.

С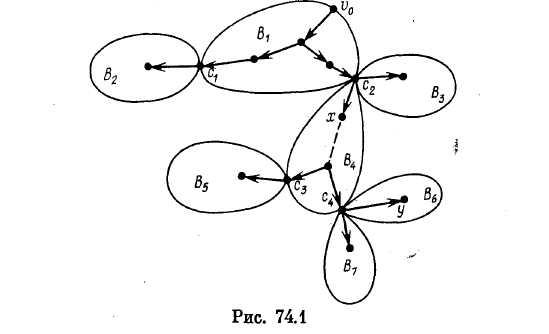ледующие два утверждения показывают, каким образом поиск в глубину «реагирует» на точки сочленения графа.

Утверждение 74.2. Вершина vo является точкой сочленения графа G тогда и только тогда, когда она име­ет не менее двух сыновей.

Пусть v₀ — точка сочленения графа G. Ясно, что каждый блок графа, включающий вершину v₀, содержит по крайней мере одного из ее сыновей.

Пусть теперь s₁ , s₂, ..., s_k — сыновья вершины v₀. Рассмотрим поддеревья T_Si (i = 1, k). Ясно, что VG— v₀ = U VT_Si. Для доказательства несвязности графа G — v₀ достаточно показать, что в этом графе нет ребер, связывающих вершины различных T_Si. Но это сразу сле­дует из утверждения 74.1.

Будем говорить, что х — собственный предок (пото­мок) вершины у, если х — предок (потомок) у и х ≠ у.

Утверждение 74.3. Вершина v≠v₀ является точ­кой сочленения графа G тогда и только тогда, когда для некоторого сына s этой вершины не существует дуги (х, у) € В такой, что х — потомок (не обязательно соб­ственный) вершины s, а у — собственный предок вер­шины v.

Пусть v — точка сочленения графа G и G₁, G₂, ..., G_m, m ≥ 2,— блоки этого графа, содержащие верши­ну v. Пусть, далее, v' = F(v), т. е. v' — отец вершины v.Не теряя общности считаем, что вершина v' содержится в блоке G₁. Каждый из остальных блоков G_i(i = 2, m)должен, очевидно, содержать хотя бы одну вершину, яв­ляющуюся сыном вершины v. Пусть, например, s — сын вершины v и s € G₂. Если теперь допустить существование «обратного» ребра ab (т. е. дуги (а, b)€ В) такого, что а — потомок s, а b — собственный предок вершины v,то придем к существованию в графе G простого цикла,содержащего вершины v' и s. Этот цикл образован простой (а,b)-цепью, состоящей из «прямых» ребер и «об­ратного» ребра ab. Это означает (согласно утвержде­нию 36.3), что вершины s и v' принадлежат одному бло­ку. Получили противоречие.

Докажем теперь вторую часть утверждения. Пусть вершина s является сыном вершины v, для которого выполняется условие, фигурирующее в формулировке ут­верждения. Это условие вместе с утверждением 74.1 озна­чает, что если ab—«обратное» ребро и а € Т_а, то либо b € Т_а, либо b = v. Последнее означает, что все ребра графа G, связывающие вершины множества VT_а с верши­нами VG\VT_а, инцидентны вершине v, т. е. v-—точка со­членения графа G.

Перейдем теперь непосредственно к разработке алго­ритма выделения блоков графа. Чтобы уяснить схему применения ПГ к решению этой задачи, обратимся к при­меру.На рис.74.1 изображен граф «с точностью до бло­ков». ПГ начинается в вершине v₀. После нескольких ша­гов придем в одну из точек сочленения графа, например, в c₂. Пусть, далее, выбирается и помечается как «прямое» ребро c₂x блока В₄. После этого дальнейшая работа ПГ вплоть до возвращения в c₂ происходит точно так, как если бы было v₀ = c₂ и блоков В₁, В₂, В₃ в графе G не было бы вовсе. Поэтому возвращение в Сг из х будет оз­начать, что пройдены все ребра блоков В₄ , В₅, В₆.,В₇ .Таким образом, возвращение в c₂ произойдет позже, чем возвращения в c₃ и c₄ из висячих блоков В₅, В₆.,В₇. Эти рассмотрения приводят к следующему важному выводу. Самое первое возвращение в точку сочленения произой­дет сразу же после завершения обхода всех ребер некото­рого висячего блока В_к. Это же справедливо и по отно­шению к дальнейшему поведению ПГ в графе, получен­ном из графа G удалением блока B_h.

Покажем, как использовать сказанное выше в пред­положении, что у нас есть способ, позволяющий при каждом возвращении из вершины v в F(v) определять, является ли F(v) точкой сочленения. С этой целью заве­дем стек S, в который будем заносить всякое ребро гра­фа G сразу после получения им пометки «прямое» или «обратное». Таким образом, все ребра добавляются в конец списка S. Пусть в нашем примере возвращение из вершины у в c₄ (см. рис. 74.1) является самым первым возвращением в точку сочленения. Тогда к моменту воз­вращения в c₄ ребра блока В₆ будут занимать все t по­следних мест в стеке S, где t — число ребер этого блока. Важно при этом, что ребро c₄ у занимает первое среди t указанных мест. Это позволяет, просматривая стек S справа налево, выделить (т. е., например, переместить з отдельный список) все ребра блока В₆. Затем эти ребра удаляются из S.

Итак, учитывая сказанное, необходимо уметь в про­цессе ПГ быстро определять возвращение в вершину, являющуюся точкой сочленения. Утверждения 74.2 и 74.3 дают соответствующие критерии, и нам надо их «алгорит­мизировать». С этой целью для каждой вершины v € VG шределим множество P(v). В это множество включим вершину v и каждого ее предка w, для которого существует «обратное» ребро xw такое, что х — потомок вершины v в остовном глубинном дереве Т. Иными словами, множество P(v) состоит из всех предков вершины v, которых можно достичь из v, проходя сначала несколько (возможно, ни одной) дуг дерева Т, а затем одну дугу множества В.

Введем теперь функцию l(v), v € VG, полагая l(v) = min ПГ(x). Например, в графе на рис. 73.1 l(l) = 1, l(2) = 1, l(3) = l, l(4) = 3, l(5) = 1, l(6)=3, l(7)=3.

Используя функцию l(v), сформулируем утверждение 74.3 в следующем виде, более удобном для организации вычислений.

Утверждение 74.4. Вершина v≠v₀ является точкой сочленения графа G тогда и только тогда, когда су­ществует такой сын s этой вершины, что l(s)≥ ПГ(v).

Вычислить значениеl(v) нетрудно, если известны значения функции l для всех сыновей вершины v. Именно, если s₁, s₂ , ..., s_m — сыновья вершины v, то имеет место формула

Справедливость этого соотношения становится очевид­ной, если заметить следующее. Множество предков вер­шины v, достижимых из нее с использованием дуг дере­ва Т и не более одной дуги из В, состоит из предков v, достижимых таким же способом из вершин s₁, s₂ , ..., s_m и множества вершин, к которым ведут обратные ребра от вершины v.

Используя соотношение (1), функцию l можно вычис­лять попутно с выполнением обычных операций поиска в глубину. При первом посещении вершины v вместе с присвоением ПГ-номера полагаем l(v) = ПГ(v). В даль­нейшем это значение корректируется в соответствии с формулой (1) следующим образом. Всякий раз, когда происходит возвращение в вершину v из некоторого ее сына s, полагаем l(v):=min{l(s), l(v)}. Кроме того, ког­да некоторое ребро vw помечается как «обратное», пола­гаем l(v):=min{l(v), ПГ(w)}. К моменту возвращения из v в вершину x=F(v) будет вычислено истинное зна­чение l(v), которое в дальнейшем используется для кор­ректировки l(х). Существенно, что каждая из этих кор­ректировок требует только O(1) дополнительного време­ни. Поэтому ПГ вместе с вычислением функции l по-прежнему будет выполняться за время O(|EG|+|G|).

Еще одна добавка к «стандартному» поиску в глубину связана с точками сочленения. Для обнаружения точки сочленения достаточно после каждого возвращения в вер­шину v из некоторого ее сына s сравнить величины l(s) и ПГ(v). Если окажется, что l(s) ≥ ПГ(v), то все ребра стека S, начиная с последнего и кончая sv, удаляются из этого списка. Удаленные ребра составляют один из бло­ков графа G. Согласно утверждению 74.4 неравенство l(s) ≥ ПГ(v) означает, что либо вершина v — точка со­членения, либо v = v₀ и v не является точкой сочленения. Заметим, что второй случай не требует особого рассмот­рения. В этом случае удаленные из стека S ребра соот­ветствуют единственному блоку графа, содержащему v₀. И, наконец, последняя деталь. Выделение блока графа G мы понимаем как удаление всех ребер этого блока из стека S. Можно считать, что одновременно с удалением из S каждое такое ребро заносится в некоторый другой список, причем множество ребер разных блоков разделе­ны в этом списке, например, символом 0. Процедура по­строения этого нового списка очевидна, и чтобы не за­громождать описания алгоритма, мы не приводим ее в явном виде.

Сравнение l(s) с ПГ(v) производится |G| — 1 раз, и, следовательно, суммарное время, затраченное на выпол­нение сравнений, составляет O(|G|). Каждое ребро гра­фа один раз включается в стек S и один раз исключается из него. Поэтому вся работа, связанная с изменением S, выполняется за время O(|EG|). Таким образом, поиск в глубину вместе с выделением блоков будет выполняться за время O(|EG|+|G|).

Алгоритм A2 поиска в глубину с выделением двусвязных компонент.

1.ПГ(v₀):=1, l(v_o):=1, S:=¢, F(v₀):=0, T:=¢, В:= ¢, k :=1,p:= 1, Q(1):= v₀.

2.v:=Q(p).

3.Просматривая список N_v, найти такую вершину w,что ребро vw не помечено, и перейти к п. 4. Если таких вершин нет, то перейти к п. 5.

4. Если вершина w имеет ПГ-номер, то поместить реб­ро vw как «обратное», занести ребро vw в стек S, l(v): = min{l(v), ПГ(w)} [выполнена корректировка l(v)].Перейти к п. 3 и продолжить просмотр списка N_v. Иначе ребро vw пометить как «прямое», k := k + 1, ПГ(w):=k,l(w):=k, F(w):= v,p:=p + 1, Q(p):= w. Перейти к п. 2.

5. р := р — 1. Если р = 0, то конец. Иначе перейти к п. 6.

6.Пусть x = F(v). Если l(v)> ПГ(x), то перейти к п. 7. Иначе l(x):= {l(x), l(v)} [выполнена корректи­ровка 1{х)] и перейти к п. 2.

7.Удалить из стека S все ребра вплоть до xv [уда­ленные ребра составляют блок графа G]. Перейти к п. 2.

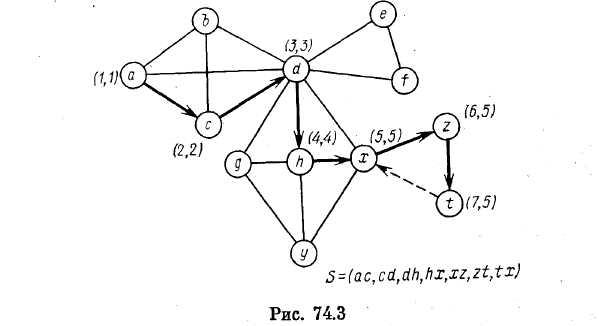
Пример. На рис. 74.2 изображен граф G и приве­дены списки смежности его вершин. Этот граф имеет че­тыре блока В₁ , В₂ , В₃ , В₄ и две точки сочленения d и х. Поиск в глубину начинается с вершины α, т. е. v_o=α. На рис. 74.3 отражена ситуация, сложившаяся непосред­ственно перед выделением блока В₄. К этому моменту шесть ребер помечены как «прямые» и одно как «обрат­ное». Прямые ребра проведены жирными линиями, а об­ратное — пунктирной. Тем и другим придана соответ­ствующая ориентация. Помеченные ребра расположены в стеке S в том порядке, в котором они получали помет­ки. Пара чисел (α, β), приписанная вершине v, имеет сле­дующий смысл: α = ПГ(v), a β — значение l(v), вычис­ленное к рассматриваемому моменту.

П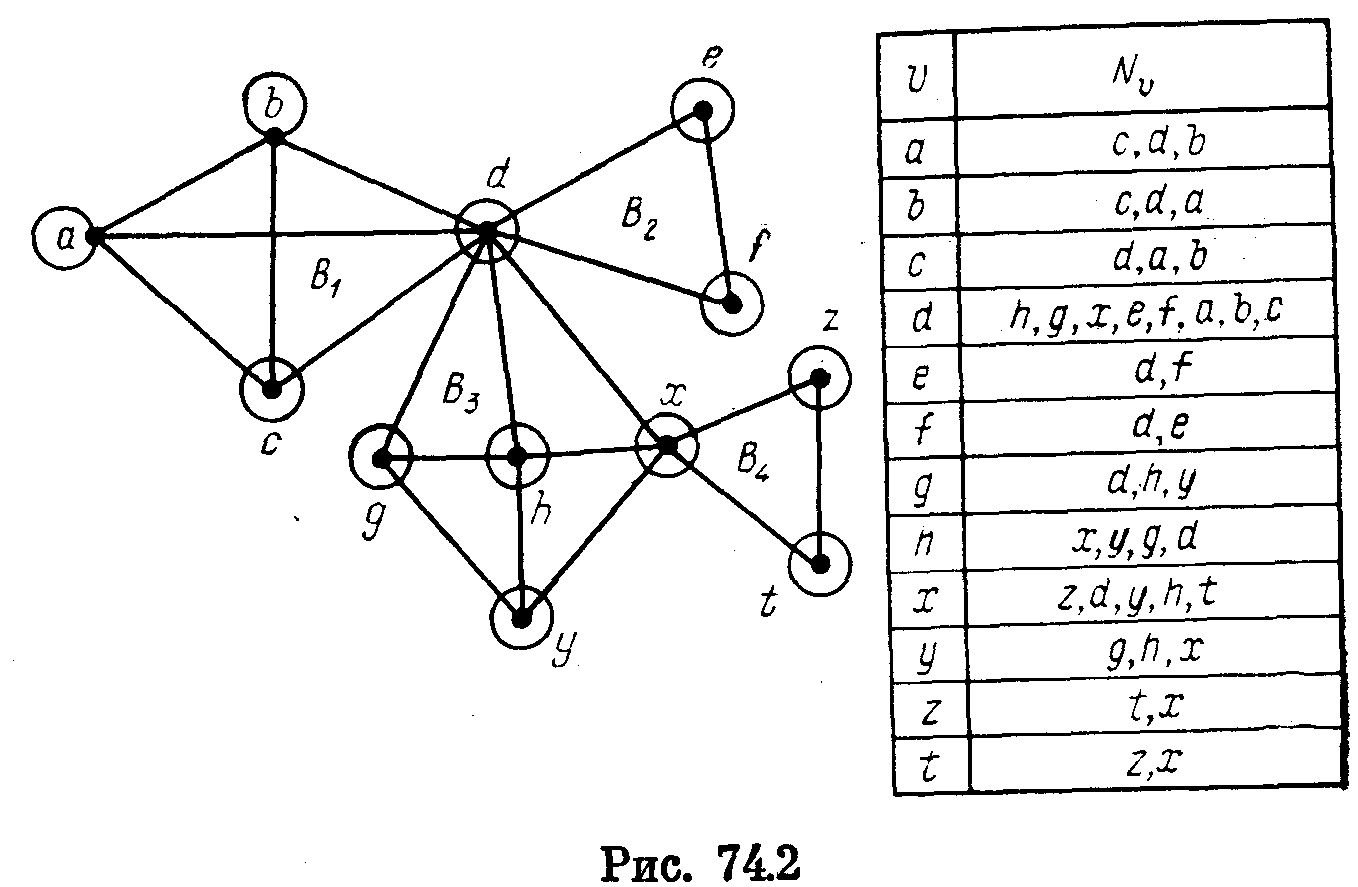осле того, как реброtx получило пометку «обратное», произошло возвращение в вершину z. При этом сравнение величин ПГ(z)=6 и l(t) = 5 показало, что вершина z не является точкой сочленения. Далее при возвращении

из вершины z в х обнаруживается, что l(z) = 5 = ПГ(x). Следовательно, все ребра от tx до xz в стеке S составля­ют блок графа G. Эти ребра —tx, tz, xz — удаляются из S, и тем самым выделен блок В₄..

После этого алгоритм работает так, как если бы бло­ка В₄. в графе G не было вообще. Ключевые моменты

д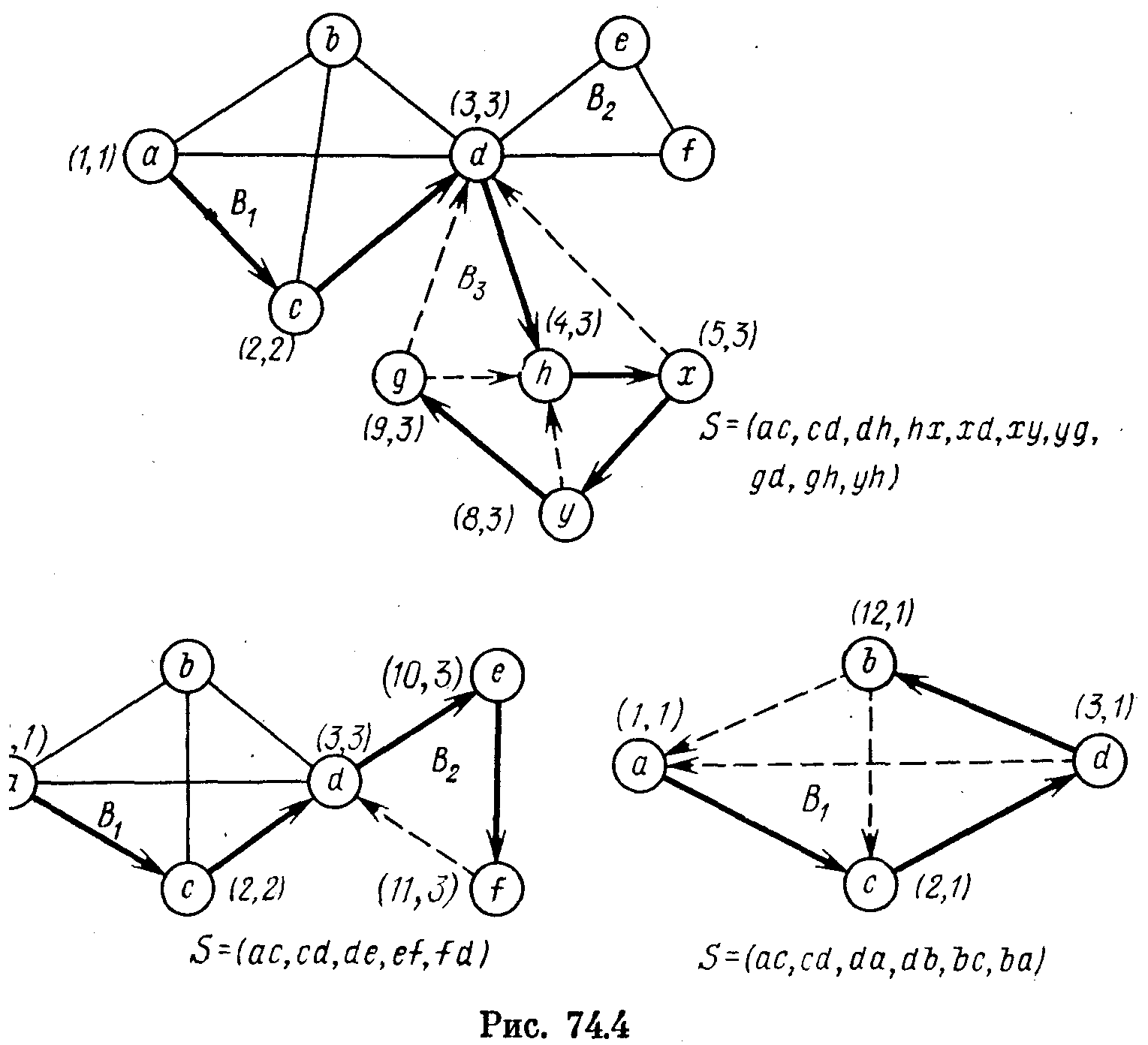альнейшей работы алгоритма иллюстрируются нарис. 74.4. Каждый из трех графов (вместе с их помет­ками и стеком S), изображенных на этом рисунке, отра­жает ситуацию, создавшуюся непосредственно перед уда­лением очередного блока. Выделение последнего блока, т.е. удаление его ребер из стека S, произойдет при возвращении в вершину v₀ = а, для которой ПГ (а) = 1 =l(с). Таким образом, на вершину v_o — a алгоритм реагирует» точно так же, как на точку сочленения.

В заключение отметим, что поиск в глубину оказывается полезным и при отыскании 3-связных компонент графа. Известен основанный на поиске в глубину алгоритм, решающий эту задачу за время O(|EG|+|G|).