
§ 75. Минимальный остов
Задача о минимальном остове состоит в отыскании остова минимального веса во взвешенном графе (G, w). Она считается одной из самых «легких» оптимизационных задач на графах. Решение этой задачи можно получить с помощью «жадного» алгоритма, если указать процедуру» которая по любому ациклическому множеству ребер X € EG и ребру е € EG определяет, содержит ли множество ребер X U е цикл графа G. В качестве такой процедуры можно использовать, например, поиск в глубину, поскольку выявление цикла в множестве X U е, где е = ab, равнозначно отысканию (a, b) -цепи в порожденном подграфе G(X). В процессе работы «жадного» алгоритма эта процедура выполняется не более |Е| раз, и, следовательно, затраты времени составят O(|EG|•|G|). Для упорядочения множества EG по неубыванию весов известны алгоритмы сложности O(|EG|log|G|). Таким образом, даже бесхитростная реализация «жадной» стратегии поиска минимального остова приводит (независимо от способа задания графа G) к алгоритму сложности O(|EG|•|G|), т. е. к полиномиальному алгоритму. С этой точки зрения задача о минимальном остове действительно является легкой.
Мы сейчас рассмотрим два алгоритма решения этой задачи, имеющие лучшие оценки быстродействия.
Пусть T = {( T1, V1,), (V2, T2), ...,(Vk, Tk)}-остовный лес взвешенного графа G, Vi и Тi — множества вершин и ребер i-й компоненты леса Т, w(x, у)—вес ребра ху графа G. Оба алгоритма построения минимального остова опираются на следующую простую теорему.
Теорема 75.1. Пусть ребро аb имеет минимальный вес среди всех ребер, у которых ровно один конец содержится в VT1. Тогда среди остовов графа G, содержащих Т U ab, найдется такой, вес которого не более веса любого остова, содержащего Т.
![]() Пусть
Т'
—
произвольный остов графа G,
содержащий
T
и не содержащий ребра аb.
Добавим
это ребро к Т'.
Полученный
граф будет содержать цикл S
(теорема
13.1). Этот цикл включает ребро ab
и
по крайней мере
еще одно ребро а'b',
у
которого ровно один конец содержится
в V1.
По
условию w(a,
b)≤(a',
b').
Следовательно,
Пусть
Т'
—
произвольный остов графа G,
содержащий
T
и не содержащий ребра аb.
Добавим
это ребро к Т'.
Полученный
граф будет содержать цикл S
(теорема
13.1). Этот цикл включает ребро ab
и
по крайней мере
еще одно ребро а'b',
у
которого ровно один конец содержится
в V1.
По
условию w(a,
b)≤(a',
b').
Следовательно,
С другой стороны, граф T’+ab — a’b' является остовом графа G, содержащим Т U ab.
Замечание.
Легко показать, что каждый минимальный
остов должен содержать по крайней мере
одно из
ребер минимального веса графа G.
Следовательно,
всякий
алгоритм построения минимального остова
должен хотя
бы раз просмотреть всю входную информацию,
будь то
матрица весов, список ребер или списки
смежности графа.
В противном случае непросмотренное
ребро может
оказаться единственным ребром минимального
веса
графа, и
это
ребро не сможет войти в минимальный
остов.
Теорема сразу подсказывает следующую стратегию построения минимального остова. На первом шаге рассмотрим остовный лес Т1 с n=|G| компонентами. Каждая его компонента состоит из одной вершины, т. е. Vi1 = {vi}. Этот лес, очевидно, содержится в любом остове графа G. Среди ребер, инцидентных vi , выберем ребро минимального веса v1vx1 и присоединим его к Т1. Согласно теореме 75.1 существует минимальный остов, содержащий лес Т2 = Т1 U {v1vx1}, у которого компонента (V12, T12) cодержит две вершины v1 и vx1 и ребро v1vx1k ,а остальные компоненты одновершинные. На следующем шаге будет выбрано и добавлено к Т2 ребро минимального веса среди ребер, соединяющих, {v1 ,vx1} с VG\{v1, vh1} и т. д.
И![]() так,
стратегия построения минимального
остова совершенно
ясна: на каждом шаге присоединяется
ребро, минимальное
по весу среди ребер, соединяющих уже
построенный
фрагмент минимального остова с вершинами,
еще
не включенными во фрагмент. Нам остается
только позаботиться
об экономной реализации шагов этого
провеса.
С этой целью свяжем с каждой вершиной
х
€
VG.
Две
метки α
(х)
и
β(х),
смысл
которых заключается в следующем.
Пусть проделано k
шагов
и (V1k,
T1k)
—
фрагмент
минимального остова, построенный к
этому моменту,
т. е. это компонента леса, к которой на
предыдущих этапах
присоединялись ребра минимального
веса. Тогда
так,
стратегия построения минимального
остова совершенно
ясна: на каждом шаге присоединяется
ребро, минимальное
по весу среди ребер, соединяющих уже
построенный
фрагмент минимального остова с вершинами,
еще
не включенными во фрагмент. Нам остается
только позаботиться
об экономной реализации шагов этого
провеса.
С этой целью свяжем с каждой вершиной
х
€
VG.
Две
метки α
(х)
и
β(х),
смысл
которых заключается в следующем.
Пусть проделано k
шагов
и (V1k,
T1k)
—
фрагмент
минимального остова, построенный к
этому моменту,
т. е. это компонента леса, к которой на
предыдущих этапах
присоединялись ребра минимального
веса. Тогда
Таким образом, α (х) — вес минимального по весу ребру, соединяющего вершину х с построенным фрагментом мимального остова, а β(х)—имя второй вершины это-ребра. Метки α(х) и β(х) позволяют быстро находить в каждом шаге ребро минимального веса. Кроме того, после присоединения очередной вершины v к фрагменту ветки легко подкорректировать. Для этого достаточно сравнить «старое» значение α(х) с w(v, x) и выбрать из них меньшее в качестве «нового» значения α(х).
В приводимом ниже описании алгоритма построения минимального остова помимо α(х) и β(х) использованы следующие обозначения: VT, ЕТ — множества вершин и ребер строящегося фрагмента минимального остова; Nx —окружение вершины х; |G| = п. Граф G задан матрицей весов.
Алгоритм A3 построения минимального остова.
Положить ЕТ := ¢, VT := {а}, где а — любая вершина из VG. Каждой верщине х ≠ а приписать метки α(х)= w(x, а), если x €Na, и α(x)= ∞, если x ¢ Na, β(x) = а.
[
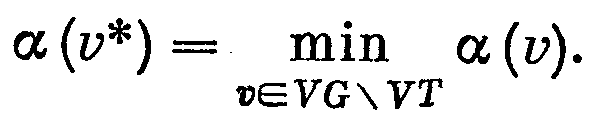 отыскание
вершины, «ближайшей» к фрагменту].Выбрать
вершину v*
€
VG\VT
согласно
условию
отыскание
вершины, «ближайшей» к фрагменту].Выбрать
вершину v*
€
VG\VT
согласно
условию
[увеличение фрагмента]. Пусть v‘= β(v *). Изменить VT и ЕТ, полагая VT := VT U {v*}, ЕТ : = ET U v'v*.
Если |VT| = n , то конец. Ребра, находящиеся в множестве ЕТ, составляют минимальный остов.
Для каждой вершины v € Nv* ∩ (VG\VT) изменить метки следующим образом. Если α(v)> w(v*, v),то α(v):= w(v*, v), β(v):= v*. Если же а(v) ≤ w(v*, v),то метку вершины v не менять. Перейти к п. 2.
Утверждение 75.2. Алгоритм A3 строит минимальный остов за время O(|G|2).
Так как всякий раз к ЕТ добавляется ребро, один конец которого принадлежит VT, а другой нет, то граф Т = (VT, ЕТ) на каждом шаге является деревом. После завершения работы алгоритма это дерево будет остовным, поскольку алгоритм прекращает работу только если VT = VG.
Докажем минимальность остова Т. Для этого достаточно доказать, что после k-го (k = 1, п— 1) выполнения п. 3 алгоритма граф Тк = (VTh, ETh) содержится в некотором минимальном остове. Доказывать будем индукцией по k. При k = 1 наше утверждение непосредственно следует из теоремы 75.1. Предположим, что оно справедливо для некоторого k > 1, т. е. граф Тк, построенный в результате k выполнений п. 3, содержится в некотором минимальном остове. Учитывая правило выбора ребра е для присоединения к Th, применим теорему 75.1. Получим, что граф Th+1 = Тк U е, построенный в результате (k + 1)-го выполнения п. 3, также содержится в некотором минимальном остове.
Выясним теперь быстродействие алгоритма. Однократное выполнение п. 2 требует времени не более O(|G|). Столько же времени достаточно для обновления меток в п. 5, а п. 3 и п. 4 выполняются за время O(1). Поскольку каждый из пп. 2—5 выполняется п — 1 раз, то оценка трудоемкости алгоритма — O(|G|2).
Пример 1. На рис. 75.1 изображены граф G и последовательность Тi (I = 1, п — 1) фрагментов минимального остова, получающихся после каждой итерации алгоритма. Числа, приписанные ребрам графа G, означают
в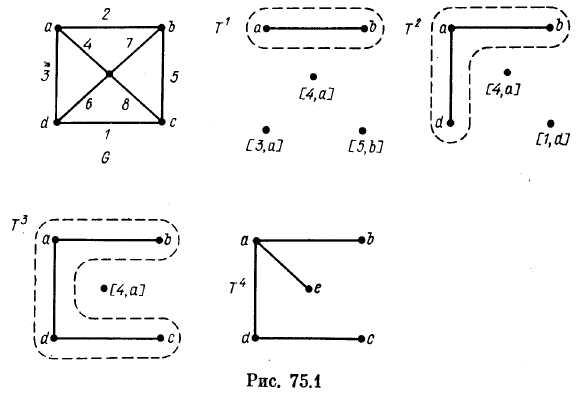 еса
этих ребер. Каждой вершинех,
еще
не вошедшей в
Тi
приписана
пара чисел [α(x),
β(x)],
которыми она помечена
в результате i-го
выполнения п. 5 алгоритма.
еса
этих ребер. Каждой вершинех,
еще
не вошедшей в
Тi
приписана
пара чисел [α(x),
β(x)],
которыми она помечена
в результате i-го
выполнения п. 5 алгоритма.
Если граф G задан матрицей весов, то всякий алгоритм построения минимального остова в таком графе будет иметь сложность не менее чем O(|G|2), поскольку он, согласно замечанию 1, должен просматривать все элементы матрицы весов. Следовательно, в этой ситуации алгоритм A3 имеет неуменьшаемую по порядку трудоемкость. Если же граф G задан списком ребер либо списками смежности и |EG| существенно меньше чем |G|2, то быстродействие алгоритма A3 далеко от оптимального. Другими словами, алгоритм A3 недостаточно эффективен в применении к «редким» графам, т. е. к графам, слабо насыщенным ребрами.
Рассмотрим еще один алгоритм построения минимального остова, ориентированный на работу именно с такими графами. Этот алгоритм (алгоритм A4), как и предыдущий, опирается на теорему 75.1, однако более полно использует предоставляемые ею возможности. Именно, если в алгоритме A3 ребро присоединяется всякий раз к одной и той же компоненте леса, то в алгоритме A4 ребра присоединяются к каждой компоненте.
Пусть T = {( V1, Т1), ..., (Vp, Tp)} — остовный лес графа G. Назовем ребро аb минимальным по весу для компоненты (Vl ,Tl),1 ≤ l ≤ p, если a € Vl ,b¢ Vl и w(a,b)=min w(x,y). Будем говорить, что М = М(Т) - множество минимальных по весу ребер для леса T, если для каждого l = 1, р множество М содержит хотя бы одно минимальное по весу ребро для компоненты (Vl ,Tl) и, кроме того, М — минимальное по включению множество, обладающее этим свойством.
Утверждение 75.3. Если М — множество минимальных по весу ребер для T={( V1, Т1), ..., (Vp, Tp)}, то граф Т' = Т + М не содержит циклов.
Доказываем от противного. Предположим, что Т содержит цикл S, который не теряя общности будем считать простым. Пусть a1b1 , a2b2 , ... , albl — ребра множества S ∩ М, выписанные в той последовательности, как они расположены в цикле S. Этой последовательности соответствует последовательность компонент (Vk1, Tk1), (Vk2 , Tk2) , ..., (Vkl , Tkl) леса Т, такая, что а1 € Vk1, b1 € Vk2, a2 € Vk2 , b2 € Vk3 , ..., аl € Vkl , bl € Vkl.. Выберем среди ребер аibi ( i = 1, l) максимальное по весу. Пусть это будет ребро а1b1 . Ясно, что а1b1 является минимальным по весу ребром по крайней мере для одной из компонент (Vkl , Tkl) или (Vk2 , Tk2). He теряя общности считаем, что ребро а1b1 — минимальное по весу для (Vk1, Tk1). Тогда w(а1 , b1)=w(аi , bi) и, следовательно, множество M \ а1b1 содержит хотя бы одно минимальное по весу ребро для каждой компоненты леса Т. Последнее противоречит минимальности множества М.
Перейдем теперь к изложению алгоритма A4.Этот алгоритм, так же, как и A3, на первой итерации имеет дело с остовным лесом графа G, состоящим из п=|G| одновершинных компонент. Каждая итерация алгоритма состоит в следующем. Вначале строится множество М минимальных по весу ребер для леса Т, полученного в результате предыдущих итераций. (Важно отметить, что сделать это можно за один просмотр элементов множества EG.). Затем с помощью поиска в глубину выделяются связные компоненты графа Т' = Т + М, который согласно утверждению 75.2 является лесом. После этого начинается следующая итерация с новым лесом Т’ имеющим, очевидно, меньше компонент, чем Т.
В приводимом ниже описании алгоритма A4 используются следующие обозначения. Ребра графа G содержатся в списке Е, т. е. E(i)—пара номеров концевых вершил i-го ребра. Список W содержит веса ребер графа G, т. е. W(i)—вес i-го ребра. Чтобы каждый раз строить множество минимальных по весу ребер для текущего леса заюдин просмотр списка Е, используются списки НМР, BMP и КОМП:
НМР (i)—номер минимального по весу ребра для i-й компоненты текущего леса;
BMP (i)—вес этого ребра;
КОМП (j)— номер компоненты текущего леса, содержащей вершину j.
Пусть, далее, ЕТ — множество ребер текущего леса Т, а р — число его компонент; Е1 — множество минимальных по весу ребер для текущего леса Т.
Алгоритм A4 построения минимального остова.
ЕТ:=¢, КОМП(i):=i, ВМР(i):=∞ для i = 1,n , р:= п. [Пп. 2—8 —построение множества Е1 минимальных по весу ребер для леса Т].
k:=1.
Пусть E(k) = uv; i:=КОМП(u), j:=КОМП(v) [i и j — номера компонент леса, содержащих вершины и и v соответственно].
Если i≠ j, то перейти к п. 5, иначе перейти к п. 7.
Если w(u, v)= W(k) < BMP (j), то BMP (j): = w(u, v), HMP(j):=k.
Если w(u, v)=W{k)<BMP(i), то ВМР(i): =w(u, v), HMP(i):=k.
Если k = |EG|, то перейти к п. 8. Иначе k := k +1 и перейти к п. 3. [К моменту выполнения п. 8 первые р элементов НМР содержат номера ребер, составляющих множество минимальных по весу ребер для Т.]
Просмотреть первые р элементов массива НМР и сформировать множество Е1 минимальных по весу ребер для леса Т.
9.ET:=ET U Ei [ЕТ — множество ребер «нового» леса Т'].
10. Выделить с помощью алгоритма поиска в глубину связные компоненты графа Т' = Т + E1 [обновлен список КОМП, получено новое значение р].
11. Если р = 1, то конец [ЕТ — множество ребер минимального остова]. Иначе перейти к п. 2.
Утверждение 75.4. Алгоритм A4 строит минимальный остов за время O(|EG| log |G|).
 Нетрудно
убедиться, что после каждого выполнения
п. 8 множество E1
является множеством минимальных
по весу ребер для леса Т,
рассматриваемого
в этот момент.
Поэтому согласно утверждению 75.2 граф
Т'
=
Т +
Е1
снова
является остовным лесом. Это означает,
Нетрудно
убедиться, что после каждого выполнения
п. 8 множество E1
является множеством минимальных
по весу ребер для леса Т,
рассматриваемого
в этот момент.
Поэтому согласно утверждению 75.2 граф
Т'
=
Т +
Е1
снова
является остовным лесом. Это означает,
что алгоритм строит некоторый остов графа G. Минимальность этого остова доказывается с помощью теоремы 75.1 точно так же, как при обосновании предыдущего алгоритма.
Выясним теперь быстродействие алгоритма A4. Для однократного выполнения каждого из пп. 3—6 достаточно времени O(1) и, следовательно, построение Е1 осуществляется за время O(|EG|). Таких же затрат достаточно и для однократного выполнения пп. 8—11. Таким образом, затраты на переход от Т к Т' = Т + Е1 (т. е. на выполнение одной итерации) составляют O(|EG|) операций. Оценим теперь число итераций алгоритма. Поскольку одно ребро может быть минимальным по весу не более чем для двух компонент леса Т, то на каждой итерации |Е1| ≥ р(Т)/2.А так как Т + Ех — лес,то р(Т+ Е1< <р(Т)/2, т. е. на каждой итерации число компонент уменьшается по крайней мере вдвое. Это означает, что число итераций алгоритма не превосходит log |G|, следовательно, он строит минимальный остов за время O(|EG|log|G|).
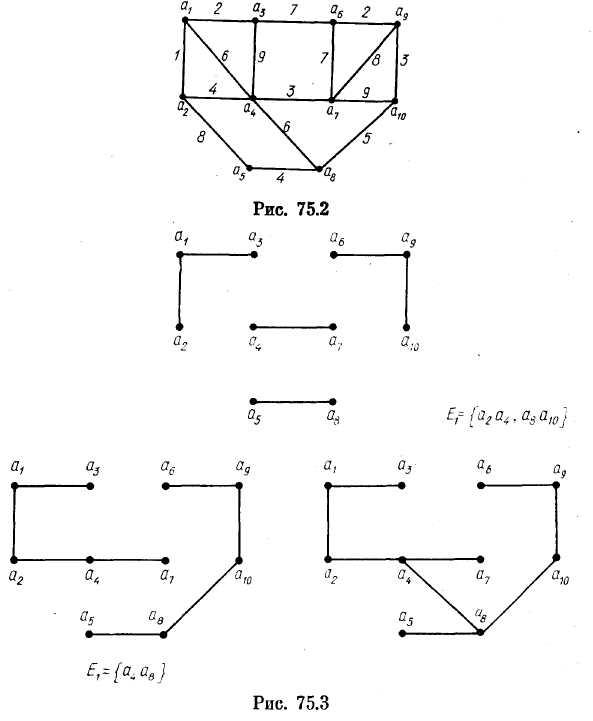
Пример 2. Применим алгоритм A4 к графу, изображенному на рис. 75.2. На первой итерации будет найдено множество Е1 = { а1a2 ,а1a3 ,а4 a7 ,а5 a8 ,а6 a9 ,а9 a10 } минимальных по весу ребер для леса, имеющего одновершинные компоненты. Остовные леса, полученные в результате выполнения 1-й, 2-й и 3-й итераций, изображены на рис. 75.3. Последний из них является минимальным остовом.
