Исследование функций ПНИПУ

Федеральное агентство по образованию

Государственное образовательное учреждение

высшего профессионального образования

ПЕРМСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

Исследование функций и построение графиков

Индивидуальные задания

Пособие разработано ст. преп. Роговой Н. В.

Одобрено методической комиссией кафедры «Высшая математика»

© 2007, каф. «Высшая математика» ПГТУ

Пермь 2007

План исследования функции

1. Найти область определения функции.

Определение. Областью определения функции называется совокупность всех значений независимой переменной , для которых функция определена.

2. Определить является функция четной, нечетной или общего вида.

Определение. Функция , определенная на множестве , называется четной, если выполняется условие и , называется нечетной, если выполняется условие и .

График четной функции симметричен относительно оси , график нечетной – относительно начала координат.

Если функция является четной или нечетной, то исследование можно провести только для и при построении графика воспользоваться его симметричностью.

3. Определить является ли функция периодической.

Определение. Функция , определенная на множестве , называется периодической на этом множестве, если существует такое число , что для и . При этом число называется периодом функции.

Наименьшее положительное число , удовлетворяющее равенству , является основным периодом функции.

Если функция периодическая, то исследование проводится на любом интервале, длина которого совпадает с основным периодом функции.

4. Определить координаты точек пересечения графика с осями координат, определить интервалы знакопостоянства функции.

5. Найти наклонные (в т.ч. горизонтальные) асимптоты и вертикальные асимптоты графика функции.

Прямая является вертикальной асимптотой графика функции , если или , где - точка разрыва или граничная точка области определения функций.

Прямая является горизонтальной асимптотой графика функции , если существует предел .

Прямая является наклонной асимптотой графика функции , если существуют пределы и .

При нахождении этих пределов удобно пользоваться правилом Лопиталя.

6. Найти точки экстремума и интервалы возрастания (убывания) функции.

Определение. Функция называется возрастающей (убывающей), если большему значению аргумента соответствует большее (меньшее) значение функции.

Возрастание и убывание функции характеризуется знаком ее производной .

Достаточные условия возрастания (убывания) функции. Если функция дифференцируема на интервале и для , то эта функция возрастает (убывает) на .

Определение. Точка называется точкой максимума (минимума) функции, если существует такая -окрестность точки , что для всех из этой окрестности выполняется неравенство , ().

Максимум и минимум функции называется экстремумом функции. Функция может иметь экстремум только в тех точках, которые принадлежат области определения функции и в которых первая производная равна нулю или не существует. Такие точки называются критическими.

Достаточные условия экстремума

I Если непрерывная функция дифференцируема в некоторой  - окрестности точки и при переходе через нее (слева направо) производная меняет знак с плюса на минус, то есть точка максимума, с минуса на плюс, то - точка минимума.

II Если в точке первая производная функции равна нулю , а вторая производная существует и отлична от нуля , то в точке функция имеет экстремум. Если - максимум, если - минимум.

7. Найти точки перегиба и интервалы выпуклости (вогнутости) графика функции.

Определение. График дифференцируемой функции называется выпуклым (вогнутым) на интервале , если он расположен выше (ниже) любой ее касательной на этом интервале.

Теорема. Если функция во всех точках интервала имеет отрицательную вторую производную , то график функции в этом интервале выпуклый. Если же - график вогнутый.

Точка графика непрерывной функции , отделяющая его части выпуклости и вогнутости, является точкой перегиба.

Достаточное условие существования точек перегиба. Если вторая производная при переходе через точку , в которой она равна нулю или не существует, меняет знак, то точка графика с абсциссой есть точка перегиба.

Результаты проведенного исследования функции рекомендуется свести в таблицу, в первой строке которой указываются все значения , выделенные в результате исследования, как самой функции , так и ее производных и , а также интервалы, на которые данными точками разбивается область определения. Во второй строке указываются значения функции на каждом из выделенных интервалов. В третьей строке выделяются критические точки функции и указывается знак первой производной на каждом интервале. В четвертой строке – знак второй производной на каждом интервале. В последней строке по знакам определяется характер монотонности функции, по знакам выпуклость (вогнутость) графика функции, а также определяется характер выделенных точек (точки максимума, точки минимума, точки перегиба).

Построение графика функции рекомендуется начать с обозначения на координатной плоскости точек, выделенных в таблице и построения асимптот (если они есть). Для более точного построения можно вычислить значения функции в дополнительных точках.

Приведем примеры полного исследования функции:

Пример 1:

1. Область определения:

2.

функция нечетная.

3. Функция не является периодической.

3. 

-нули функции.

3. Функция непрерывна на всей области определения, поэтому вертикальных асимптот нет.

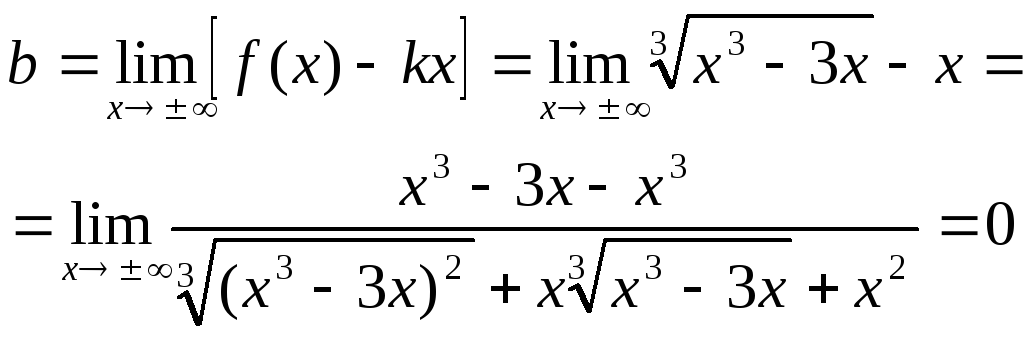
Прямая является наклонной асимптотой графика функции.

3. Найдем первую производную:

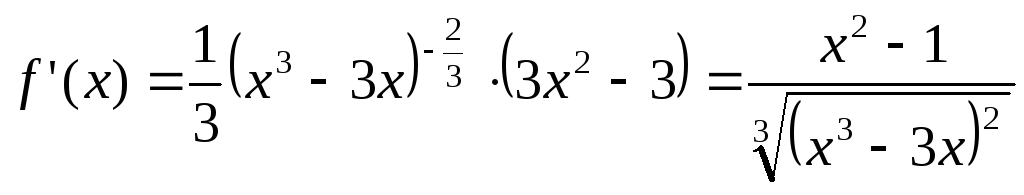
при ,

не существуют при , ,

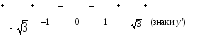
Используя достаточные условия экстремума, получаем, что - точка минимума, -точка максимума.

3. Найдем вторую производную:

не существует при

В точках , , - перегиб графика.

Составим таблицу:

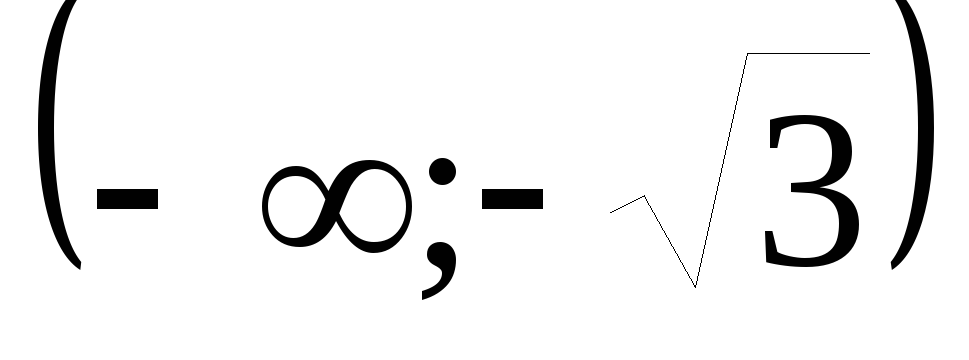
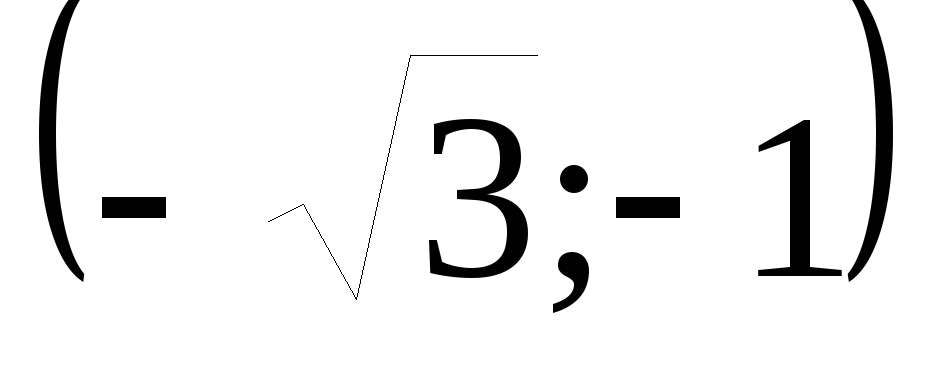
				-1	(-1;0)
	-	0	+		+
	+		+		-
	+		-		-
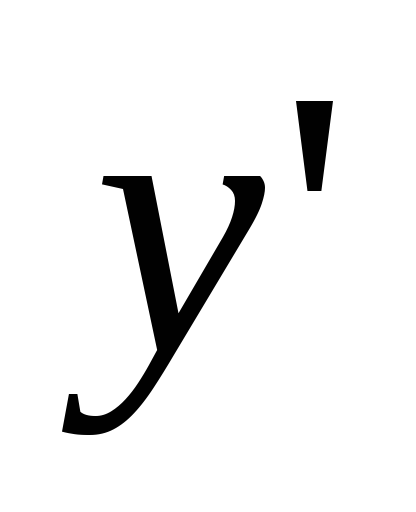
		перегиб		max

Продолжение таблицы

	0	(0;1)	1
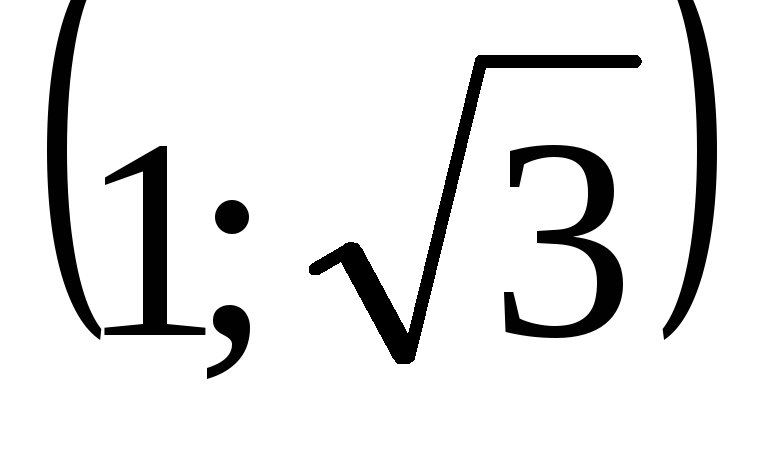
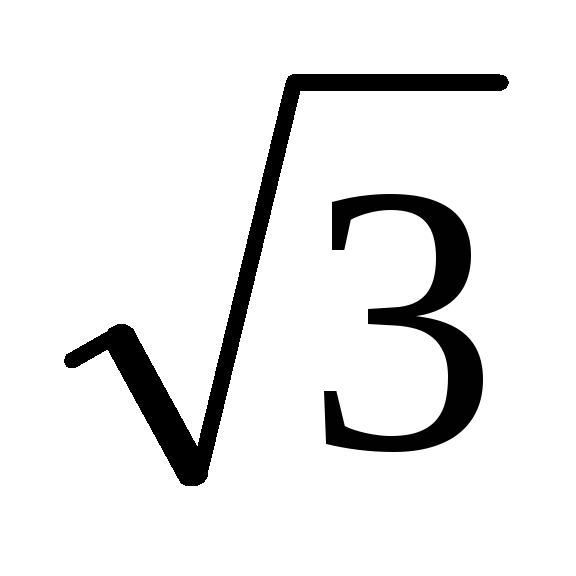
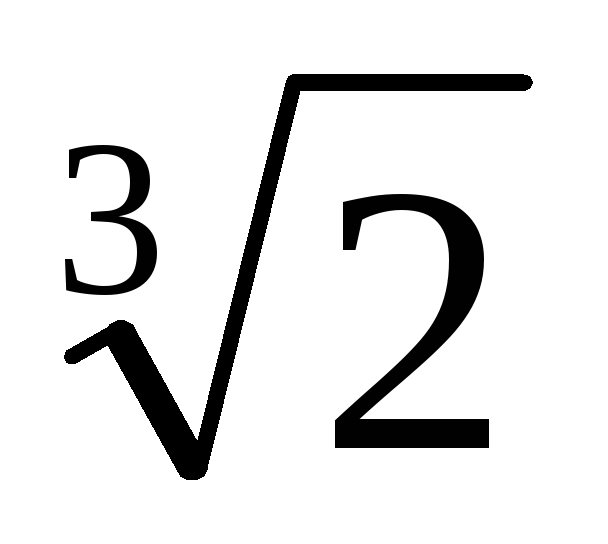
	0	-	-	-	0	+
		-		+		+
		+		+		-
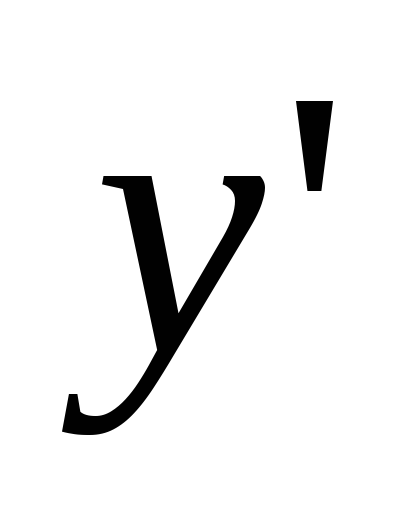
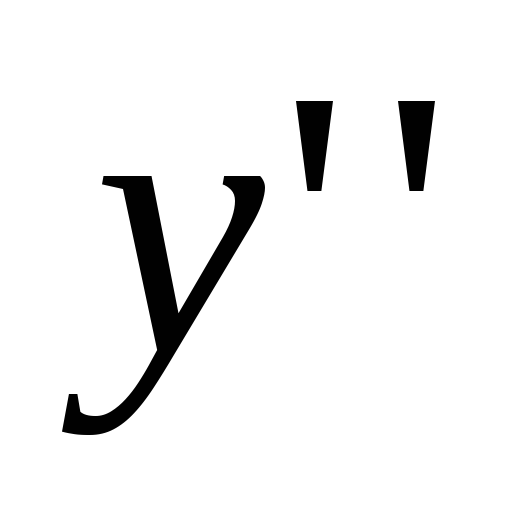
			min		перегиб

Строим график функции (рис.1).

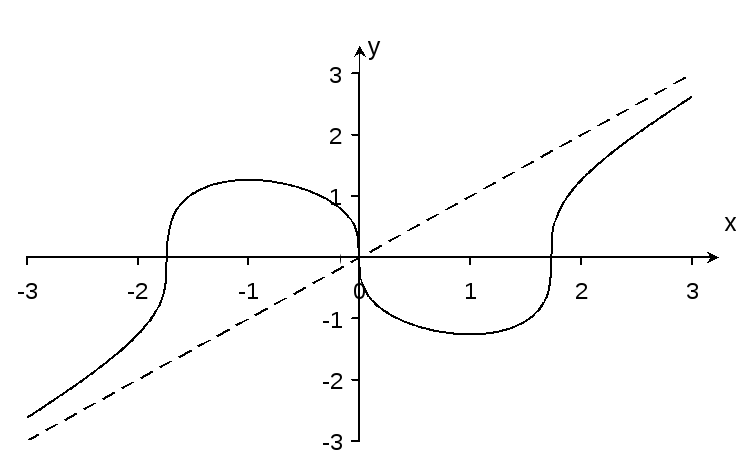
Рис.1

Пример 2:

1. Область определения:

2.

функция четная. Дальнейшее исследование проведем для .

3. Функция не является периодической.

4. при

5. Поскольку и - точки разрыва

и ,

, ,

то и - вертикальные асимптоты.

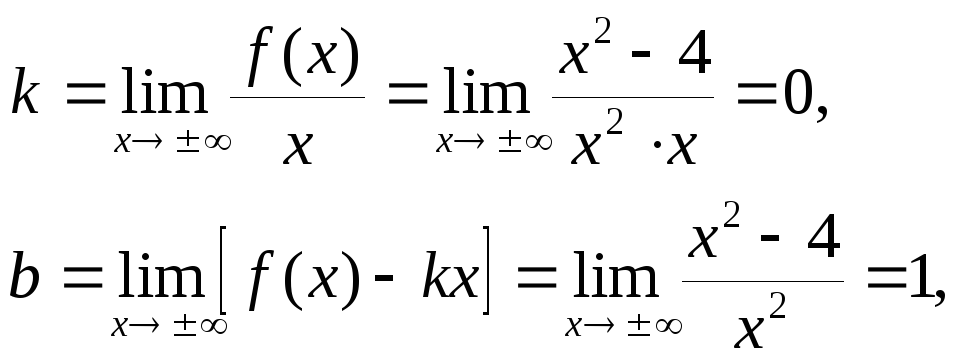
- горизонтальная асимптота.

6. Найдем первую производную:

при

не существует при .

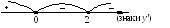
- точка максимума.

7. Найдем вторую производную:

при

не существует при

Т.к. при функция не определена, то точек перегиба нет.

Составим таблицу:

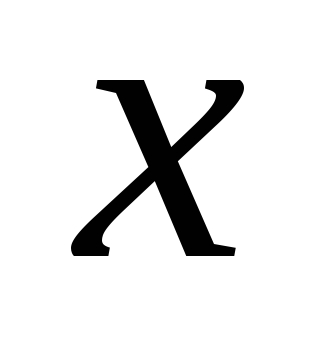
	0	(0;2)	2
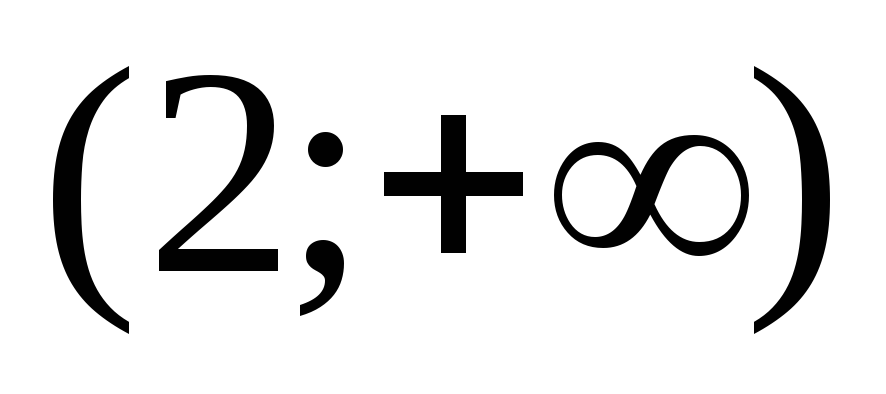
	0	-	Не существует	+
		-		-
		-		+
	max		Вертикальная асимптота

Строим график функции для , затем на интервале строим линию, симметричную относительно оси (рис.2).

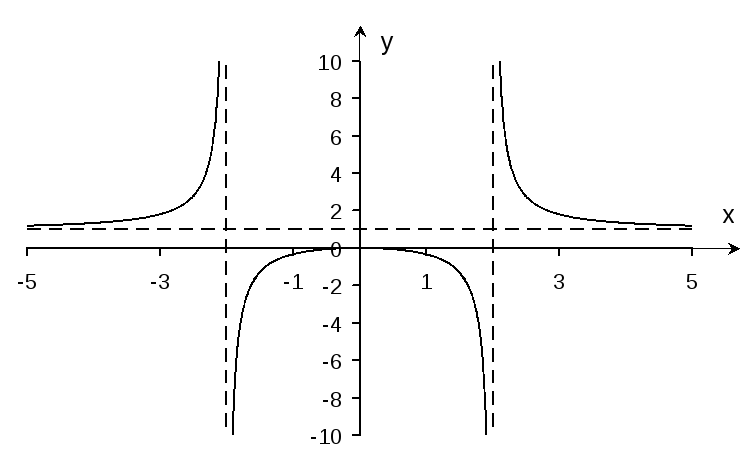
Рис.2

Пример 3:

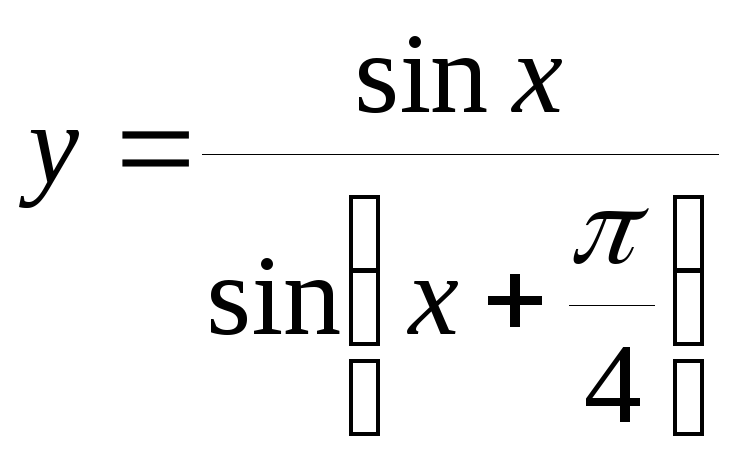
1. Область определения:

Функция определена для всех , для которых ,

т.е. .

2. Функция не является ни четной, ни нечетной.

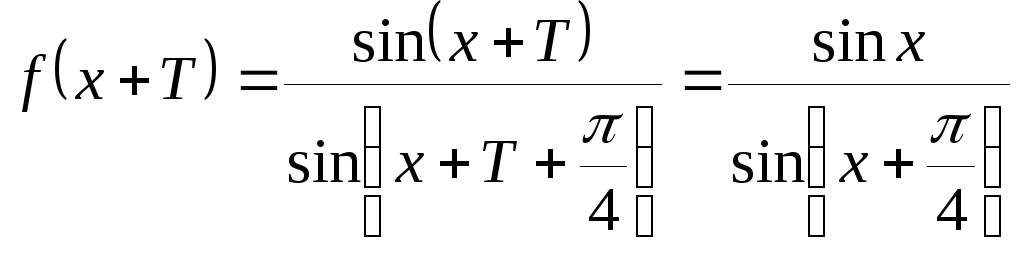3. при

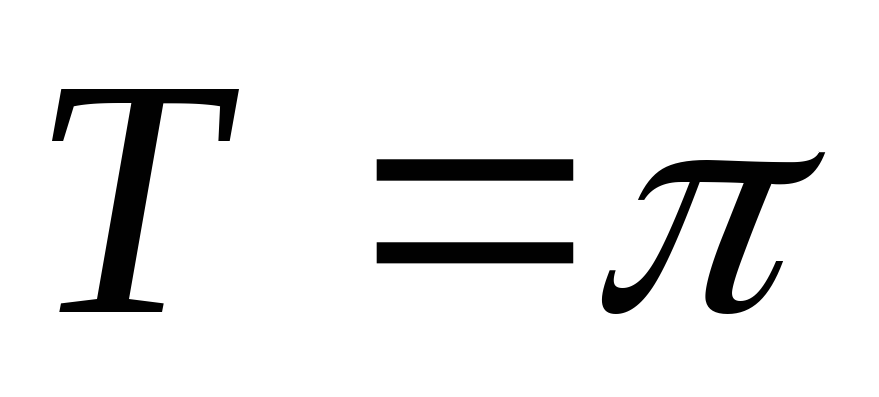
- основной период, основной промежуток .

4. при .

Промежутку принадлежат точки .

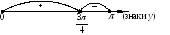
5. В промежутке одна точка разрыва , в остальных точках функция непрерывна.

, .

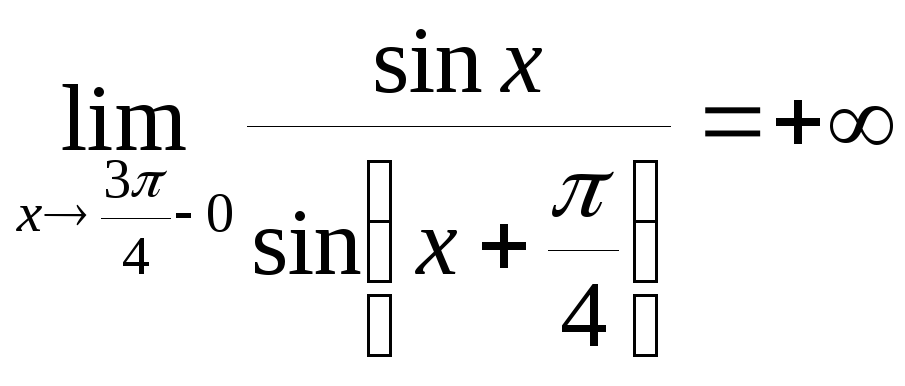Прямая - вертикальная асимптота.

Наклонных и горизонтальных асимптот нет.

6. Найдем первую производную:

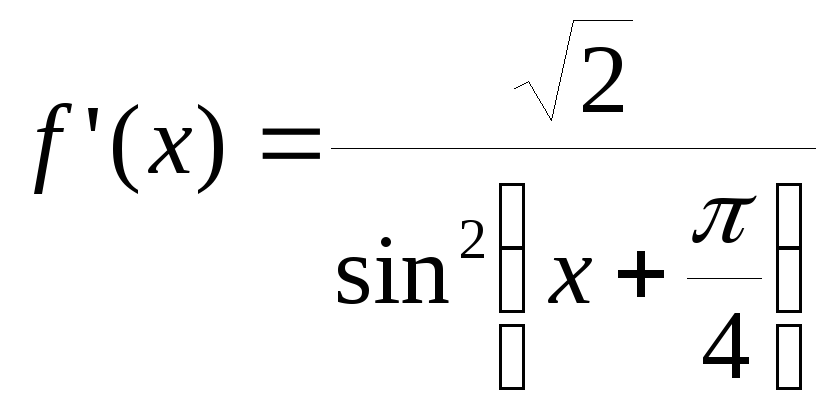
при ,

не существует при .

Cледовательно, точек экстремума нет.

7. Найдем вторую производную:

, если ,

т.е.

Из этого множества промежутку принадлежит точка .

не существует при .