2. Решатели оду в matlab

Данный раздел посвящен описанию возможностей, предоставляемых MATLAB, для численного решения задач Коши и краевых задач для обык­новенных дифференциальных уравнений произвольного порядка и систем, включая краевые задачи с неизвестными параметрами и вырождающимися коэффициентами. Рассматривается также решение дифференциальных урав­нений с запаздывающим аргументом. Для решения этих задач предназначе­ны специальные функции MATLAB в вычислительной математике их на­зывают солверы. MATLAB имеет достаточно большой набор солверов, ос­нованных на различных численных методах.

Для решения задачи Коши в MATLABсуществует семь солверов:

Таблица №1

ode45	Одношаговые явные методы Рунге-Кутта 4-го и 5-го порядка. Это классический метод, рекомендуемый для начальной пробы решения. Во многих случаях он дает хорошие результаты
ode23	Одношаговые явные методы Рунге-Кутта 2-го и 4-го порядка. При умеренной жесткости системы ОДУ и низких требованиях к точности этот мето;. может дать выигрыш в скорости решения
ode113	Многошаговый метод Адамса-Башворта-Мултона переменного порядка Это адаптивный метод, который может обеспечить высокую точность решения
ode23tb	Неявный метод Рунге-Кутта в начале решения и метод, использующий формулы обратного дифференцирования 2-го порядка в последующем
ode15s	Многошаговый метод переменного порядка (от 1 до 5, по умолчанию 5), использующий формулы численного дифференцирования. Это адаптивный метод, его стоит применять, если решатель ode45 не обеспечивает решения
ode23s	Одношаговый метод, использующий модифицированную формулу Розенброка 2-го порядка. Может обеспечить высокую скорость вычислений при низкой точности решения жесткой системы дифференциальных уравнений
ode23t	Метод трапеций с интерполяцией. Этот метод дает хорошие результаты при решении задач, описывающих колебательные системы с почти гармоническим выходным сигналом

Методика их использова­ния одинакова, включая способы задания входных и выходных аргументов:

Таблица №2

[T.Y]=solver(@F,tspan,у0)	Где вместо solver подставляем имя конкретного решателя — интегрирует систему дифференциальных уравнений вида у'=F(t,y) на интервале tspan с начальными условиями у0. @F — дескриптор ODE-функции. Каждая строка в массиве решений Y соответствует значению времени, возвращаемому в векторе-столбце Т
[T.Y]=solver(@F,tspan,y0, options)	Дает решение, подобное описанному выше, но с параметрами, определяемыми значениями аргумента options, созданного функцией odeset. Обычно используемые параметры включают допустимое значение относительной погрешности RelTol (по умолчанию le-З) и вектор допустимых значений абсолютной погрешности AbsTol (все компоненты по умолчанию равны 1е-6)
[T.Y]=solver(@F,tspan,y0, options,pl,p2...)	Дает решение, подобное описанному выше, передавая дополнительные параметры pi, р2,... в m-файл F всякий раз, когда он вызывается. Используйте options=[], если никакие параметры не задаются
[T.Y.TE.YE.IE]=solver(@F, tspan,y0,options)	В дополнение к описанному решению содержит свойства Events, установленные в структуре options ссылкой на функции событий. Когда эти функции событий от (t, у, равны нулю, производятся действия в зависимости от значения трех векторов value, isterminal, di rection (их величины можно установить в m-файлах функций событий). Для i-й функции событий value(i) —значение функции, isterminal (i) — прекратить интеграцию при достижении функцией нулевого значения, direction^) = 0, если все нули функции событий нужно вычислять (по умолчанию), +1 — только те нули, где функция событий увеличивается, -1 — только те нули, где функция событий уменьшается. Выходной аргумент ТЕ — вектор-столбец времен, в которые происходят события (events), строки YE являются соответствующими решениями, а индексы в векторе IE определяют, какая из i функций событий (event) равна нулю в момент времени, определенный ТЕ. Когда происходит вызов функции без выходных аргументов, по умолчанию вызывается выходная функция odeplot для построения вычисленного решения. В качестве альтернативы можно, например, установить свойство OutputFcn в значение ' odephas2' или 'odephas3' для построения двумерных или трехмерных фазовых плоскостей
[T.X.Y]=sim(@model, tspan,y0,options,ut,p1,р2..„)	Использует модель SIMULINK, вызывая соответствующий решатель из нее

В достаточно общем случае вызов солвера для решения задачи Коши про­изводится следующим образом:

[Т, У] = solver(odefun,interval,Y0,options)

где odefun — функция для вычисления вектор-функции правой части сис­темы уравнений, interval — массив из двух чисел, задающий промежуток для решения уравнения, Y0 - заданный вектор начальных значений иско­мой вектор-функции, options - структура для управления параметрами и ходом вычислительного процесса. Солвер возвращает массив т с координа­тами узлов сетки, в которых найдено решение, и матрицу решений Y, каж­дый столбец которой является значением компоненты вектор-функции ре­шения в узлах сетки.

Далее мы обсудим применение солверов и управление процессом решения на ряде показательных примеров из перечисленных выше классов задач.

Схема решения таких задач в MATLAB состоит из следующих этапов.

1 Приведение дифференциального уравнения к системе дифференциальных уравнений первого порядка (если изначально задана система, то в этом нет необходимости).

2 Написание специальной функции для системы уравнений.

3 Вызов подходящего солвера.

4 Визуализация результата.

Разберем решение дифференциальных уравнений на примере уравнения второго порядка:

y'' + 2y' + 10y = sint.

Соответствующие начальные усло­вия имеют вид:

y(0) = 1, y’(0) = 0.

Теперь исходную задачу надо привести к системе дифференциальных уравнений. Для этого вводят столько вспомо­гательных функции, каков порядок уравнения. В данном случае необходи­мы две вспомогательные функции у1 и у2, определяемые формулами:

y₁ = y, y₂ = y’.

Система уравнений с начальными условиями требуемая для работы такова:

y₁’ = y₂; y₁(0) = 1;

y₂’ = -2y₂ - 10 y₁ + sint; y₂(0) = 0.

Второй этап состоит в написании функции для системы дифференциальных уравнений. Функция должна иметь два входных аргумента: переменную t, по которой производится дифференцирование, и вектор, размер которого равен числу неизвестных функций системы. Число и порядок аргументов фиксированы, даже если t явно не входит в систему. Выходным аргументом функции является вектор правой части системы. Текст функции oscil для разбираемого примера приведен в листинге1.

Входными аргумента­ми солверов в самом простом случае являются: указатель на функцию (или ее имя в апострофах), вектор с начальным и конечным значением времени наблюдения за процессом и вектор начальных условий. Выходных аргумен­тов два: вектор, содержащий значения времени, и матрица значении иско­мых функций в соответствующие моменты времени. Значения функций рас­положены по столбцам матрицы, в первом столбце - значения первой функции, во втором - второй и т. д. В силу проделанных замен первый столбец матрицы содержит как раз значения неизвестной функции входящей в исходное дифференциальное уравнение а второй столбец — значения ее производной. Как правило, размеры матрицы и вектора достаточно велики, поэтому лучше сразу отобразить результат на гра­фике. Пример:

function solvdem

% формирование вектора начальных условий

Y0 = [1; 0];

% вызов солвера от функции oscil, начального и конечного

% времени и вектора начальных условий

[T, Y] = ode113(@oscil, [0 15], Y0);

% вывод графика решения исходного дифференциального уравнения

% (маркеры - точки, линия - сплошная)

plot(T, Y(:, 1), 'r.-')

% вывод графика производной от решения исходного

% дифференциального уравнения (маркеры - точки, линия - пунктир)

hold on

plot(T, Y(:, 2), 'k.:')

% вывод пояcнений на rpaфик

title(' {\ity} \prime\prime+2{\ity} \prime+10{\ity} = sin{\itt}')

xlabel('\itt')

ylabel( '{\ity), (\ity) \prime ')

legend ('y(t) ', 'v(t)', 4)

grid on

hold off

% подфункция вычисления правых частей уравнения

function F = oscil(t, y)

F = [y(2); -2*y(2) - 10*y(1) + sin(t)];

В результате применения солвера на экран выводятся графики:

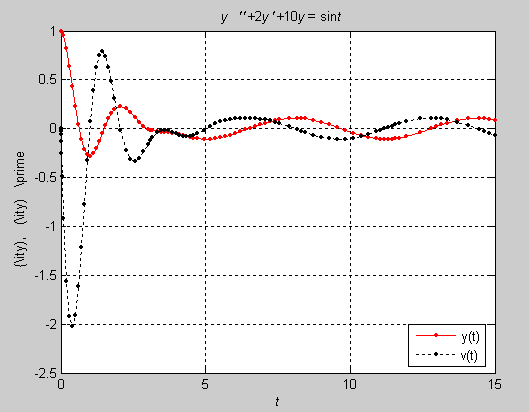
В нашем примере решение задачи Коши для системы дифференциальных уравнений, соответствующей исходной задаче для дифференциального уравнения второго порядка, было получено при помощи солвера ode113, который основан на методе Адамса—Бэшфорта—Милтона. Кроме солвера ode113, MATLAB имеет еще ряд солверов для задачи Коши: ode45, ode23, ode15s, ode23s, ode23t_f ode23tb, интерфейс которых не отличается от ode113.

При выборе солвера для решения задачи необходимо учитывать свойства системы дифференциальных уравнений, иначе можно получить неточный результат или затратить слишком много времени на решение.

Выбор солвера для решения задачи Коши

В данном разделе описана стратегия применения солверов MATLAB для решения обыкновенных дифференциальных уравнений или систем с на­чальными условиями.

Очень часто солвер ode45 даст вполне хорошие результаты, им стоит вос­пользоваться в первую очередь. Он основан на формулах Рунге—Кутты четвертого и пятого порядка точности. Солвер ode23 также основан на формулах Рунге—Кутты, но уже более низкого порядка точности. Имеет смысл применять ode23 в задачах, содержащих небольшую жесткость, когда требуется получить решение с невысокой степенью точности. Если же тре­буется получить решение нежесткий задачи с высокой точностью то наи­лучший результат даст od113, основанный на методе переменного порядка Адамса-Бэшфорта-Милтона. Солвер ode113 оказывается особенно эф­фективным для нежестких систем дифференциальных уравнении, правые части которых вычисляются по сложным формулам. Все солверы пытаются найти решение с относительной точностью 10^-3 и абсолютной - 10^-6, Хо­рошим тестом качества приближенного решения является увеличение точ­ности вычислений (задание точности вычислении и ряда других параметров описано в следующем разделе).

Если все попытки применения ode45, ode23s, ode113 не приводят к успеху, то возможно, что решаемая система является жесткой. Для решения жестких систем подходит солвер ode15s, основанный на многошаговом методе Гира, который допускает изменение порядка. Если требуется решить жесткую за­дачу с невысокой точностью, то хороший результат может дать солвер ode23s, реализующий одношаговый метод Розенброка второго порядка.

Простейшее использование вышеперечисленных солверов производится так же, как и odell3 При решении практических задач важно контролировать вычисления. Все солверы допускают задание ряда параметров, позволяющих повысить эф­фективность вычислении в зависимости от решаемой задачи. В частности, при решении жестких задач задание якобиана системы позволяет увеличить быстродействие вычислений. Одной из важнейших характеристик прибли­женного решения является его точность.

Управление процессом решения

Эффективное решение дифференциальных уравнений невозможно без по­нимания основных вопросов, связанных с численными методами. Солверы MATLAB не являются "черными ящиками". Пользователю необходимо выбрать подходящий солвер, в зависимости от свойств решаемой задачи, и произвести необходимые установки, обеспечивающие получение при­ближенного решения с требуемыми свойствами, например, с заданной точностью.

Солверы допускают указание параметров для контроля и управления вычислительным процессом.

Таблица №3

NormControl	Управление ошибкой в зависимости от нормы вектора решения [on | {off}].Установите 'on', чтобы norm(e) <= max(RelTol*norm(y), AbsTol). По умолчанию все решатели используют более жесткое управление по каждой из составляющих вектора решения
RelTol	Относительный порог отбора [положительный скаляр]. По умолчанию 1е-3 (0.1% точность) во всех решателях; оценка ошибки на каждом шаге интеграции e(i) <= max(RelTol*abs(y(i)), AbsTol(i))
AbsTol	Абсолютная точность [положительный скаляр или вектор {1е-6}].Скаляр вводится для всех составляющих вектора решения, а вектор указывает на компоненты вектора решения. AbsTolпо умолчанию 1е-6 во всех решателях
Refine	Фактор уточнения вывода [положительное целое число] — умножает число точек вывода на этот множитель. По умолчанию всегда равен 1, кроме ODE45, где он 4. Не применяется, еслиtspan> 2
OutputFcn	Дескриптор функция вывода [function] — имеет значение в том случае, если решатель вызывается без явного указания функции вывода,OutputFcnпо умолчанию вызывает функциюodeplot. Эту установку можно поменять именно здесь
OutputSel	Индексы отбора [вектор целых чисел] Установите компоненты, которые поступают в OutputFcn.OutputSelпо умолчанию выводит все компоненты
Stats	Установите статистику стоимости вычислений [on {off}]
Jacobian	Функция матрицы Якоби [function constant matrix]. Установите это свойство на дескриптор функцииFJac(еслиFJac(t,у)возвращает dF/dy) или на имя постоянной матрицы dF/dy
Jpattern	График разреженности матрицы Якоби [имя разреженной матрицы]. Матрица SсS(i,j)= 1, если составляющая iF(t, у) зависит от составляющей jвеличиныу, и 0 в противоположном случае
Vectorized	Векторизованная ODE-функция [on | {off}]. Устанавливается на'on', если ODE-функция FF(t,[yl y2...])возвращает вектор [F(t, yl) F(t, y2) ...]
Events	[function] — введите дескрипторы функций событий, содержащих собственно функцию в вектореvalue, и векторыisterminalиdirection(см выше)
Mass	Матрица массы [constant matrix function]. Для задачМ*у' = f(t, у)установите имя постоянной матрицы. Для задач с переменнойМвведите дескриптор функции, описывающей матрицу массы
MstateDependence	Зависимость матрицы массы от у [none | {weak} | strong]— установите'nоnе'для уравненийM(t)*y' = F(t, у). И слабая ('weak'), и сильная ('strong') зависимости означаютM(t, у), но'weak'приводит к неявным алгоритмам решения, использующим аппроксимации при решении алгебраических уравнений
MassSingular	Матрица массы М сингулярная[yes no | {maybe}](да/нет/может быть)
MvPattern	Разреженность (dMv/dy), график разреженности (см функциюspy) — введите имя разреженной матрицыSсS(i,j) = 1для любогоk, где(i, k)элемент матрицы массыM(t, у) зависит от проекции] переменнойу, и 0 в противном случае
Initial Step	Предлагаемый начальный размер шага, по умолчанию каждый решатель определяет его автоматически по своему алгоритму
Initial Slope	Вектор начального уклона ур0 ур0 = F(t0,y0)/M(t0, y0)
MaxStep	Максимальный шаг, по умолчанию во всех решателях равен одной десятой интервала tspan
BDF(Backward Differentiation Formulas) [on|{off}]	Указывает, нужно ли использовать формулы обратного дифференцирования (методы Gear) вместо формул численного дифференцирования, используемых вode15s по умолчанию
MaxOrder	Максимальный порядок ODE15S [1 | 2 | 3 |4 | 5]

Решатели используют в списке различные параметры. В приведенной ниже таблице они даны для решателей обычных (в том числе жестких) дифференциальных уравнений.

Таблица №4

Параметры	ode45	ode23	ode113	ode15s	ode23s	ode23t	ode23tb
RelTol, AbsTol, NormControl	+	+	+	+	+	+	+
OutputFcn, OutputSel, Refine, Stats	+	+	+	+	+	+	+
Events	+	+	+	+	+	+	+
MaxStep, InitialStep	+	+	+	+	+	+	+
Jacobian, JPattern, Vectorized	-	-	-	+	+	+	+
Mass	+	+	+	+	+	+	+
MStateDependence	+	+	+	+	-	+	+
MvPattern	-	-	-	+	-	+	+
MassSingular	-	-	-	+	-	+	-
InitialSlope	-	-	-	+	-	+	-
MaxOrder, BDF	-	-	-	+	-	-	-

Способ задания параметров солверов ode45, ode23, odell3, odel5s. ode23s, ode23t и ode23tb аналогичен Tому, который вы применяли при нахождении корней функции или локальных минимумов. Значения параметров записываются в управляющую структуру, которая создается функцией odeset. В общем случае обращение к odeset имеет вид:

Options = odeset (…, ‘вид контроля’, значение, …)

Параметры солверов, сгруппированные в категории по своему назначению, приведены в табл.. Следует иметь в виду, что неоправданное изменение многих параметров может повлечь уменьшение эффективности солвера или получение неверных результатов. Вызов odeset без входных аргументов позволяет посмотреть в командном окне имена всех свойств и их возможные значения, причем в фигурных скобках указаны значения, используемые солверами по умолчанию. Функция odeget предназначена для извлечения значения свойства из струк­туры

значение = odeget (options, вид_контроля)

При генерации структуры функцией odeset значение могло быть не опреде­лено, в этом случае возвращается пустой массив.

Пример выполнения задания:

Задание: Решите дифференциальное уравнение используя формулы обратного дифференцирования. Решение уравнения представьте в графическом виде. Задайте относительную точность решения и выведите ее значение на экран.

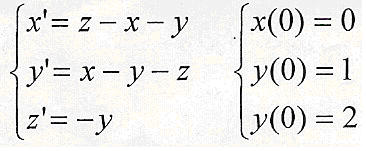
Решение:

Для решения поставленной задачи необходимо воспользоваться решателем odel5s. Именно он позволяет решить дифференциальное уравнение, используя формулы обратного дифференцирования, с помощью параметра BDF.

Приведем листинг программы:

function DIFURI

options=odeset('BDF','on','RelTol',1e-2);

odeget(options,'RelTol')

[T,Y]=ode15s(@RESH,[0 40],[0 1 2],options);

figure

for j=1:3

subplot(3,1,j); plot(T,Y(:,j),'k')

grid on

if j==1;

title('grafik X')

ylabel('X')

elseif j==2;

title('grafik Y')

ylabel('Y')

else j==3 ;

title('grafik Z')

ylabel('Z')

end

xlabel('T')

legend('ode15s',-1)

end

function dy=RESH(t,y)

dy=zeros(3,1);

dy(1)=y(3)-y(1)-y(2);

dy(2)=y(1)-y(2)-y(3);

dy(3)=-y(2);