
- •35.Дифференциальные уравнения: основные понятия и определения.
- •36.Дифференциальные уравнения с разделяющимися переменными.
- •38.Дифференциальные уравнения второго порядка, допускающие понижения порядка.
- •40.Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами.
- •37.Линейные дифференциальные уравнения первого порядка. Метод вариации произвольной постоянной. Метод подстановки.
Билет 1. Понятие производной.
Опр.
Пусть
ф-ция f(x)
определена в нек. Окрестности т.х0(U(x0)),
и пусть х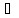 U(x0)=U(x0)\{x0}
– произвольное значение из данной
окрестности. Если
U(x0)=U(x0)\{x0}
– произвольное значение из данной
окрестности. Если
 предел отношеня
предел отношеня
 ,
х>x0,
то он называется производной ф-ции f(x)
в т. х0. Обознач. х-х0=
,
х>x0,
то он называется производной ф-ции f(x)
в т. х0. Обознач. х-х0= х,
тогда по опр. f’(x)=
х,
тогда по опр. f’(x)=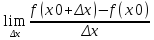 .
Пр.:f(x)=x,
f(x0+
.
Пр.:f(x)=x,
f(x0+ х)=x0+
х)=x0+ х,
f(x0)=x0,
х,
f(x0)=x0,
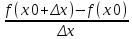 =
=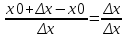 .
Пусть
f(x)
определена в нек.правосторон.(лево-)
окрестности т. х0 и
.
Пусть
f(x)
определена в нек.правосторон.(лево-)
окрестности т. х0 и
 правый (левый) предел отношения
правый (левый) предел отношения
 ,
тогда
этот предел наз прав.(левой) производной
ф-ции f(x)
в т х0.
,
тогда
этот предел наз прав.(левой) производной
ф-ции f(x)
в т х0.
 .
Теорема.
Пусть
ф-ция f(x)определ.в
нек.окрест.т.х0, тогда след.условия
эквивалентны: 1.
.
Теорема.
Пусть
ф-ция f(x)определ.в
нек.окрест.т.х0, тогда след.условия
эквивалентны: 1.
 f’(x0)
2.
f’(x0)
2.
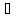 f’-(x0)=f’+(x0)
– (сущ.прав. и лев. производн.в т.х0 и они
равны). Геометр.смысл.
f’(x)опред-на
в нек. Окр.т.х0 и С. f(x),
ур-е прямой:y=y0+k(
f’-(x0)=f’+(x0)
– (сущ.прав. и лев. производн.в т.х0 и они
равны). Геометр.смысл.
f’(x)опред-на
в нек. Окр.т.х0 и С. f(x),
ур-е прямой:y=y0+k(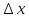 )(x-x0)(*).
Если
)(x-x0)(*).
Если

 ,
кот.получается из ур-я (*) наз касательной
графику ф-ции f(x)
в т М0. y=y0+k(x-x0).
,
кот.получается из ур-я (*) наз касательной
графику ф-ции f(x)
в т М0. y=y0+k(x-x0).
Билет 2.Понятие дифференцируемости функции в данной точке.
Опр.Пусть
ф-ция определена в нек.окре. т. х0, если
приращение дан.ф-ции в т.х0 представимо
а виде
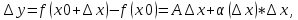 где
А- const,не
зависящая от
где
А- const,не
зависящая от
 ,
а
,
а
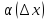 -беск.малая
ф-ция при
-беск.малая
ф-ция при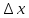 >0,
то данная ф-ция наз. Дифференцируемой
в т х0. При этом линейная(относ.
>0,
то данная ф-ция наз. Дифференцируемой
в т х0. При этом линейная(относ.
 )
часть
)
часть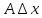 -наз.дифференциалом
ф-ци f(х)в
т х0 и обознач. dy=
-наз.дифференциалом
ф-ци f(х)в
т х0 и обознач. dy=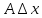 .
Теорема.f(x)
диф-ма в т х0 <=> когда в т.х0
.
Теорема.f(x)
диф-ма в т х0 <=> когда в т.х0
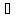 производ. Причем А=f
‘(x0).
Док-во:f(x)
– диф-ма в т.х0, т.е
производ. Причем А=f
‘(x0).
Док-во:f(x)
– диф-ма в т.х0, т.е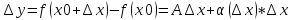 при
при
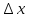 >0.
>0.
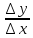 =А+d(xx).
=А+d(xx). =
=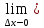 (А+d(xx))=A=f
‘(x0). Пусть
(А+d(xx))=A=f
‘(x0). Пусть
 F‘(x0),
т.е
F‘(x0),
т.е
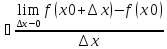 =F’(x0)=A
=F’(x0)=A
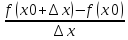 =A+
=A+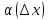 ,
где
,
где
 при
при
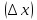 -> 0, => f
-> 0, => f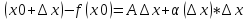 .
Опр.диф-алом
ф-ции (dy=
.
Опр.диф-алом
ф-ции (dy=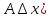 в т х0 наз-ся главная, линейная относительно
в т х0 наз-ся главная, линейная относительно
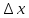 ,
часть приращения ф-ции в этой точке.
dy=f’(х0)
,
часть приращения ф-ции в этой точке.
dy=f’(х0)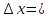 Пр.:
y(x)=x,
dx=1*
Пр.:
y(x)=x,
dx=1*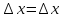 .
.
Билет 3.Свойства производных. Таблица производных.
Теорема.Пусть
имеются ф-ции f(x)
u
g(x),
определены в нек.окр. х0, имеют в дан.точке
производные. Тогда: 1. (f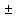 g)’=f’+g’/
2. (fg)’=f’g+fg’/
3.если g(x)
g)’=f’+g’/
2. (fg)’=f’g+fg’/
3.если g(x)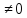 в
люб.т.из U(x0),
то (
в
люб.т.из U(x0),
то (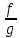 )’=
)’=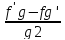 .
Теорема. Если ф-ция диф-ма в т х0, то она
непрерывна в дан. Точке. f
.
Теорема. Если ф-ция диф-ма в т х0, то она
непрерывна в дан. Точке. f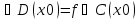 .
Док-во:
.
Док-во:
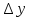 =
= при
при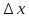 >0.
>0.
 =0
=0
Билет 4.Понятие дифференциала. Приближенное вычисление с помощью дифференциала.
Опр.диф-алом
ф-ции (dy=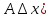 в т х0 наз-ся главная, линейная относительно
в т х0 наз-ся главная, линейная относительно
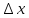 ,
часть приращения ф-ции в этой точке.
dy=f’(х0)
,
часть приращения ф-ции в этой точке.
dy=f’(х0)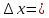 Пр.:
y(x)=x,
dx=1*
Пр.:
y(x)=x,
dx=1* .
.
/Пусть
ф-цияf(x)
 D
(x0).
F(x0)=f(x0)+f’(x0)(x-x0)+0(x-x0),
x>x0, (0(x-x0)=
D
(x0).
F(x0)=f(x0)+f’(x0)(x-x0)+0(x-x0),
x>x0, (0(x-x0)= (x-x0))
f(x0+
(x-x0))
f(x0+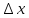 )=
f(x0)+f’(x0)
)=
f(x0)+f’(x0)
 +0(
+0(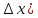 ,
,
 x>0.
При
остаточно малом значении
x>0.
При
остаточно малом значении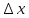 имеет место след.приближенное равенство:
F(x0+
имеет место след.приближенное равенство:
F(x0+ )
)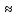 f(x0)+f’(x0)
f(x0)+f’(x0)
Билет 5.Производные и дифференциалы высших порядков.
Второй
производной наз.производную от первой
производной f(x):
у”=(f’(x))’.
Производ.n-го
порядка f(x)наз
производная от производной (n-1) порядка
f(x)ю
Теорема (ф-ма Лейбница) Пусть ф-ция f(x)
и g(x)
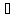 D до n-гопорядка
включительно(
D до n-гопорядка
включительно(
 f’,g’,…f(n),g(n)).
Тогда (f*g)(n)=
f’,g’,…f(n),g(n)).
Тогда (f*g)(n)=
 in
f(i)*g(n-i)=
in
f(i)*g(n-i)=
Диф-алом 1 порядка явл x и dx. Будем считать, что dx-const. Диф-алом 2порядка наз. Диф-ал от диф-ала 1 порядка= d2y=d(dy)=d(f’(x)dx)=f’(x)dx)’dx=f”(x)dx2
Билет
6.Правило Лопиталя. Раскрытие
неопределенностей. Т.Лопиталя:
пусть ф-ция f(x)
и g(x)
определены в нек.окр т а(U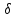 (a))
и пусть данная f(x)
(a))
и пусть данная f(x)
 D
в кажд.точке интервала окр-ти U
D
в кажд.точке интервала окр-ти U (a),
кроме ,быть может,самой т ф, и пределом
:
(a),
кроме ,быть может,самой т ф, и пределом
:
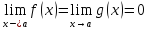
(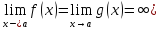 и
g’(x)
и
g’(x)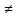 0
0
 x
x U
U (a). Тогда
если
(a). Тогда
если
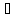 lim
lim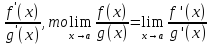
Билет 7. т.Ферма и Роля.
Т.Ферма:
пусть
ф-ция f(x)
опрд. В нек окр (a,b)
и в нек т х0 данной окр. Функция f(x)
принимает наибольшее, либо наименьшее
знач.тогда, если
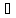 производ-я в дан. Точке f(x),
то она =0.(геометрич.смысл: если в т х0
производ-я в дан. Точке f(x),
то она =0.(геометрич.смысл: если в т х0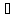 производ., то касательная ф-ции f(x),
проход. Через т х0 ||Ox.
производ., то касательная ф-ции f(x),
проход. Через т х0 ||Ox.
Т.Ролля:
пусть f(x)
опеределена на отрезке [a,b]
и выполнены след условия: 1.f(x)
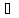 С
[a,b]
2.
С
[a,b]
2. f(x)
f(x)
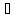 D
[a,b]
3. f(a)=f(b).
Тогда
D
[a,b]
3. f(a)=f(b).
Тогда
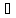 такая т с
такая т с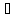 (a,b),
что f’(c)=0.
(геометрич.смысл: если вып. Условия, то
найдется такая с
(a,b),
что f’(c)=0.
(геометрич.смысл: если вып. Условия, то
найдется такая с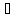 (a,b),
что касс-я, проведенная через эту точку
к f(x)
|| Ox
(a,b),
что касс-я, проведенная через эту точку
к f(x)
|| Ox
Билет8. т.Лагранжа и Коши
Т.Лагранжа:Пусть
ф-ция f(x)
определена на отрезке [a,b]
и вып.след.условия: 1. f(x)
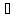 С
[a,b]
2. f(x)
С
[a,b]
2. f(x)
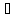 D
[a,b].
Тогда
D
[a,b].
Тогда
 т с
т с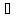 (a,b),
что
(a,b),
что
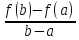 =f’(c).
(Геометрич.смысл:если вып.условия, то
=f’(c).
(Геометрич.смысл:если вып.условия, то
 такая с,3 что кас-я,проведенная к дан.т.
ф-ции f(x)
будет ||хорде, кот.проходит с координатами
((a,f(a)),(b,f(b)).
Т.Коши:
Пусть
f(x)
и g(x)
определ. на отр[a,b]
и выполнено: 1. f(x)
и g(x)
такая с,3 что кас-я,проведенная к дан.т.
ф-ции f(x)
будет ||хорде, кот.проходит с координатами
((a,f(a)),(b,f(b)).
Т.Коши:
Пусть
f(x)
и g(x)
определ. на отр[a,b]
и выполнено: 1. f(x)
и g(x)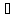 С[a,b]
2. f(x)
и g(x)
С[a,b]
2. f(x)
и g(x)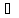 D(a,b)
3. g’(x)
D(a,b)
3. g’(x) 0
0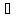 x
x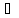 (a,b),
тогда
(a,b),
тогда
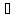 т.с
т.с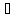 (a,b),
что вып-ся:
(a,b),
что вып-ся:

Билет
9.Признак монотонности функции.
Теорема.
Пусть f(x)
опред.на интеревала (a,b)
и
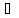 D
в каждой точке этого инервала. Тогда,
если f’(x)
D
в каждой точке этого инервала. Тогда,
если f’(x)
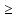 0(f’(x)
0(f’(x)
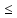 0)
0)
 x
x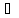 (a,b).то
f(x)
на итер-ле (a,b)
не убывает(не возрастает)Док-во: пусть
f(x)
(a,b).то
f(x)
на итер-ле (a,b)
не убывает(не возрастает)Док-во: пусть
f(x)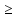 0
0 x
x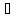 (a,b).требуется
док-ть,что
(a,b).требуется
док-ть,что
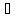 х1,х2
х1,х2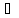 (a,b),x1
(a,b),x1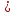 x2.
Должно выпол-ся: f(x1)
x2.
Должно выпол-ся: f(x1)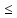 f(x2).
Фикс.х1,х2∈(a,b),
x1
f(x2).
Фикс.х1,х2∈(a,b),
x1 x2,
по формуле Лагранжа: f(x2)-f(x1)=f’(c)(x2-x1).
Где с
x2,
по формуле Лагранжа: f(x2)-f(x1)=f’(c)(x2-x1).
Где с (х1,х2).
f(x2)
(х1,х2).
f(x2)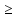 f(x1)=>f(x2)-f(x1)
f(x1)=>f(x2)-f(x1)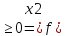 )
)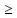 f(x1).
f(x1).
Точки
локального экстремума. Опр.точка
х0 наз лок.мин[макс], если
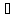 такая
окр.т.х0(х0-
такая
окр.т.х0(х0- ,х0+
,х0+ )=U
)=U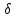 (x0),
что
(x0),
что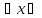 U
U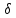 (x0)
вып-ся:f(x0)<f(x)
[f(x0)>f(x)].Опр.точки
лок.мин и лок.макс.объединены в общее
определение – точки экстремума.Теорема.Необходимое
условие точек лок.экстремума). Пусть
f(x)
имеет в т х0 лок экстремум и
(x0)
вып-ся:f(x0)<f(x)
[f(x0)>f(x)].Опр.точки
лок.мин и лок.макс.объединены в общее
определение – точки экстремума.Теорема.Необходимое
условие точек лок.экстремума). Пусть
f(x)
имеет в т х0 лок экстремум и f’(x)
в т х0(f(x)
f’(x)
в т х0(f(x) D(x0)).тогда
f’(x0)=0.
Док-во: следует из т.Ферма.дан.условие
не явл.достаточным. Теорема(достат.условие
точек лок.экстремума) пусть f(x)
D(x0)).тогда
f’(x0)=0.
Док-во: следует из т.Ферма.дан.условие
не явл.достаточным. Теорема(достат.условие
точек лок.экстремума) пусть f(x) D(U
D(U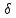 (x0)).
Тогда если f’(x)>0
[f’(x)<0]
(x0)).
Тогда если f’(x)>0
[f’(x)<0]
 (x0-
(x0- ,
x0)
и f’(x)<0
[f’(x)>0
,
x0)
и f’(x)<0
[f’(x)>0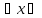 (x0,
x0+
(x0,
x0+ )]
, то х0- т.лок макс[мин].
)]
, то х0- т.лок макс[мин].
Билет 10.Направление выпуклости и точки перегиба графика функции.
Пусть
ф-ция f(x)
определена и диф-ма на интер.(a,b).
Тогда в кажд.точке (a,b)
можно построить касс-ую к графику ф-ции
f(x).
Опр.f(x)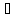 (a,b)имеет
выпуклость, направен.вниз [вверх], если
график f(x)лежит
не ниже [не выше] люб.касат.,проведенной
к точке из интер.(a,b).
Теорема: пусть на интервале (a,b)
f(x)
имеет конечную 2ю произвдную (f”(x)
(a,b)имеет
выпуклость, направен.вниз [вверх], если
график f(x)лежит
не ниже [не выше] люб.касат.,проведенной
к точке из интер.(a,b).
Теорема: пусть на интервале (a,b)
f(x)
имеет конечную 2ю произвдную (f”(x)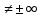 ),
тогда если f”(x)
),
тогда если f”(x)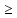 0[f”
0[f”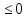 ]
]
 (a,b),
то на данном интер-ле f(x)
имеет выпуклость, направлен вниз[вверх].Опр.
т(x0
f(x0))
наз т.перегиба графика ф-ции f(x),если
(a,b),
то на данном интер-ле f(x)
имеет выпуклость, направлен вниз[вверх].Опр.
т(x0
f(x0))
наз т.перегиба графика ф-ции f(x),если
 такая
U
такая
U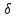 (x0),
что в дан.окр по обе стороны от т х0,
графикf(x)
имеет разное напр-е выпуклости.
Теорема(необход.условие т.перегиба)
пусть (f(x)
(x0),
что в дан.окр по обе стороны от т х0,
графикf(x)
имеет разное напр-е выпуклости.
Теорема(необход.условие т.перегиба)
пусть (f(x)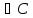 2(x0))f(x)
в т.х0 имеет непрерывн.2ю производную.
Тогда если т (х0, f(x0))
явл. Т.перегиба, то f”=0.
Теорема(достат.условие т.перегиба) Пусть
f(x)
имеет в нек.окр.т х0 производ. 2го порядка.
Тогда если в окр.дан.точки по обе стороны
от т.х0 f(x)
имеет 2ю производ. Различных знаков,
тогда т.х0 явл. т. перегиба.
2(x0))f(x)
в т.х0 имеет непрерывн.2ю производную.
Тогда если т (х0, f(x0))
явл. Т.перегиба, то f”=0.
Теорема(достат.условие т.перегиба) Пусть
f(x)
имеет в нек.окр.т х0 производ. 2го порядка.
Тогда если в окр.дан.точки по обе стороны
от т.х0 f(x)
имеет 2ю производ. Различных знаков,
тогда т.х0 явл. т. перегиба.
Билет 11.Асимптоты графика функции.
Опр.1:
если прямая
х=х0 наз
вертик.ассимптотой
к графику ф-ции f(x).
Опр.2: если
прямая
х=х0 наз
вертик.ассимптотой
к графику ф-ции f(x).
Опр.2: если

 =A(нек.число),
то прямая у=А наз гориз.ассимптотой.
Опр.3 если
=A(нек.число),
то прямая у=А наз гориз.ассимптотой.
Опр.3 если
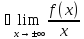 =k
и
=k
и
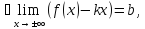 то
прямая у=kx+b
наз наклон.ассимптотой.
то
прямая у=kx+b
наз наклон.ассимптотой.
Билет 12.Схема исследования функции и построение графика.
1. Найти обл.определения ф-ции. 2.найти точки пересечения графика ф-ции с осями координат. 3. Найти асимптоты. 4. Найти точки возможного экстремума. 5. Найти критические точки. 6.исследовать знак первой и второй производной. Определить участки возрастания и убывания ф-ции, найти направлени выпуклости графика, точки экстремума и точки перегиба. 7.построить график.
Билет 13.Понятие первообразной и неопределенного интеграла. Свойства неопределенного интеграла.
Пусть
 - интервал, полуинтервал, отрезок, либо
вся числовая ось. Опр.пусть
f(x)
и f(x)
определены на промежутке
- интервал, полуинтервал, отрезок, либо
вся числовая ось. Опр.пусть
f(x)
и f(x)
определены на промежутке
 ,
причем F(x)
– диф-ма на
,
причем F(x)
– диф-ма на
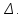 Ф-ция F(x)
наз первообразной
ф-ции f(x),если
для
Ф-ция F(x)
наз первообразной
ф-ции f(x),если
для
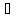 х
х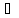
 F’(x)=f(x).
Пусть F(x)-
первообразная для ф-ции f(x)
на
F’(x)=f(x).
Пусть F(x)-
первообразная для ф-ции f(x)
на
 .
Рассмотрим ф-цию F(x)+С,
тогда F(x)+С-
тоже первообраз. f(x)
на
.
Рассмотрим ф-цию F(x)+С,
тогда F(x)+С-
тоже первообраз. f(x)
на
 .
Действительно, (F(x)+C)’=F’(x)+C=f(x).
Лемма.
Пусть F1(x)
b
F2(x)
–нек.первообразн-е для f(x)
на
.
Действительно, (F(x)+C)’=F’(x)+C=f(x).
Лемма.
Пусть F1(x)
b
F2(x)
–нек.первообразн-е для f(x)
на
 .
Тогда
.
Тогда
 такая
cont
C,
что F2(x)=F1(x)+C.
Док-во: рассмотр.ф-цию
такая
cont
C,
что F2(x)=F1(x)+C.
Док-во: рассмотр.ф-цию
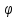 (х)=
F2(x)-F1(x)
Ф-ция
(х)=
F2(x)-F1(x)
Ф-ция
 (х)определ-а
и диф-ма на промеж-ке
(х)определ-а
и диф-ма на промеж-ке
 .
.
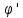 (х)=
(F2(x)-F1(x))’=F2’-F1’=f-f=0.
(х)=
(F2(x)-F1(x))’=F2’-F1’=f-f=0.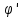 (х)
(х) 0
на промеж.
0
на промеж. по следствию из Теор. Лагранжа
по следствию из Теор. Лагранжа что
что
 (х)=С
на промеж.
(х)=С
на промеж. .
F2-F1=C
.
F2-F1=C F2=F1+C
F2=F1+C Опр.
Неопред.интегралом ф-ции f(x)
на пром-ке
Опр.
Неопред.интегралом ф-ции f(x)
на пром-ке
 наз. совокуп. Всех первообразн.ф-ции
f(x)на
наз. совокуп. Всех первообразн.ф-ции
f(x)на
 .
Фиксир. нек.первообр. f(x).Тогда
неопред.интеграл-м наз.совокуп.ф-ций
вида F(x)+C,
где С – первообр. Const,
и обозн.
.
Фиксир. нек.первообр. f(x).Тогда
неопред.интеграл-м наз.совокуп.ф-ций
вида F(x)+C,
где С – первообр. Const,
и обозн.
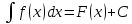 .Ф-ция
F(x)
подынтегральной ф-цией, а выраж-е f(x)dx
– подынтегральным выражением.
.Ф-ция
F(x)
подынтегральной ф-цией, а выраж-е f(x)dx
– подынтегральным выражением.
Свойства неопределенного интеграла.
-
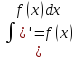 .
(F(x)+C)’=f(x).
d
.
(F(x)+C)’=f(x).
d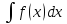 =f(x)dx,
d(F(x)+C)= (F(x)+C)’dx=f(x)dx
=f(x)dx,
d(F(x)+C)= (F(x)+C)’dx=f(x)dx -
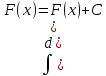
 .
. -
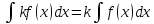
-
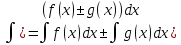
4’.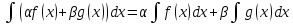
Билет 14.Свойства неопределенного интеграла. Таблица интегралов.
-
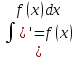 .
(F(x)+C)’=f(x).
d
.
(F(x)+C)’=f(x).
d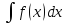 =f(x)dx,
d(F(x)+C)= (F(x)+C)’dx=f(x)dx
=f(x)dx,
d(F(x)+C)= (F(x)+C)’dx=f(x)dx -
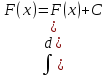
 .
. -

-
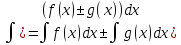
4’.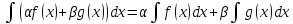
Билет
15.Основные методы интегрирования.
1.непосредственное
интегрирование.
Пр.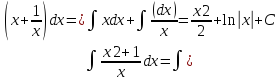
2.метод
подстановки.Теор.
пусть ф-ция
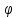 (t)
опред-на на промеж-ке
(t)
опред-на на промеж-ке
 t,
причем
t,
причем
 (t)
– диф-ма на
(t)
– диф-ма на
 t
и образом
t
и образом
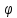 (
( t)явл.промежуток
t)явл.промежуток
 х
и фун-ция
х
и фун-ция
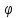 (t)явл
строго монотонной.
(t)явл
строго монотонной.
Пусть
также на пром-ке
 х
опред-на ф-ция
х
опред-на ф-ция
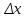 ,
кот. на
,
кот. на
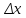 имеет первообразную F(x).
Тогда
имеет первообразную F(x).
Тогда
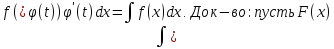 –первообр-я для ф-ции f(x).
Т.к. на промеж-ке
–первообр-я для ф-ции f(x).
Т.к. на промеж-ке
 t
определена ф-ция f
’(
t
определена ф-ция f
’( (t))
и F(
(t))
и F( (t)).
Найдем (F(
(t)).
Найдем (F(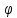 (t)))’=F
‘ (
(t)))’=F
‘ (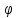 (t))
(t))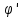 (t)=f(
(t)=f(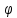 (t))
(t)) (t)
(t)
 ф-ция F(
ф-ция F( (t))
явл. первообр. ф-ции f(
(t))
явл. первообр. ф-ции f( (t))
(t))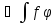 (t))
(t))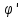 (t)dt=F(
(t)dt=F(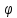 (t))+C.
Т.к.
(t))+C.
Т.к.
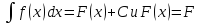 (
( (t)),
то
(t)),
то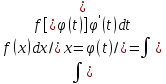
3.интегрирование
по частям.Теорема.Пусть
ф-ции u(x)
и v(x)
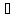 D
на нек.промеж-ке
D
на нек.промеж-ке
 .
и
.
и

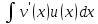 .
Тогда
.
Тогда

 ,
причем
,
причем
 Док-во: (uv)’=u’v+uv’.
d(uv)=(u’v+uv’)dx=vdu+udv.
Док-во: (uv)’=u’v+uv’.
d(uv)=(u’v+uv’)dx=vdu+udv.
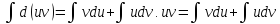
Билет 17.Определенный интеграл. Необходимое условие существования.
Пусть
ф-ция f(x)
определена на отрезке [a,b].
Разобъем отрезок [a,b]
на n
производных частей a=x<x1<x2<…<xn=b.
На каждом из отрезков [x(i-1),
xi]произвольным
образом выберем т. «кси» i [xi-1,xi].
Обозначим через
[xi-1,xi].
Обозначим через
 xi=xi-x(i-1)
и «кси»=(кси1, кси 2, … кси n).
Разбиение (a=x0<x1<…<xn=b)
обозначим через «тау». Составим сумму.
S
f(тау,
кси)=f(кси1
xi=xi-x(i-1)
и «кси»=(кси1, кси 2, … кси n).
Разбиение (a=x0<x1<…<xn=b)
обозначим через «тау». Составим сумму.
S
f(тау,
кси)=f(кси1 xi+f(кси2)
xi+f(кси2) xi+…+f(кси
n)
xi+…+f(кси
n) xi=
xi= составим такую сумму, кот.на.интегральной
суммой ф-ции f(x)
на [a,b]
с параметром кси и тау.Опр1.Пусть d(тау)
-
составим такую сумму, кот.на.интегральной
суммой ф-ции f(x)
на [a,b]
с параметром кси и тау.Опр1.Пусть d(тау)
-
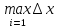 ,
- диаметр разбиения. Если
,
- диаметр разбиения. Если
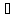 конечн.предел
конечн.предел
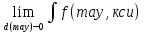 ,
не зависящей от способа разбиения
отрезка a,b
и выбора точек из набора кси, то этот
предел наз. Определенным интегралом
ф-ции f(x)
и обоз-ся
,
не зависящей от способа разбиения
отрезка a,b
и выбора точек из набора кси, то этот
предел наз. Определенным интегралом
ф-ции f(x)
и обоз-ся
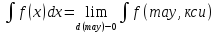 .
Необходимое
условие:
если f(x)
интегрируема на отрезке [a,b],то
она ограничена на этом отрезке. НО
обратное – неверно. Те
.
Необходимое
условие:
если f(x)
интегрируема на отрезке [a,b],то
она ограничена на этом отрезке. НО
обратное – неверно. Те
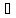 такие
ф-ции, кот.явл.ограниченными на нек.
Отрезке, но не явл.интегрироваными на
дан.отрезке.
такие
ф-ции, кот.явл.ограниченными на нек.
Отрезке, но не явл.интегрироваными на
дан.отрезке.
Билет 16. Интегрирование простейших рациональных дробей (3 вида).
Пусть
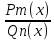 - нек.рац.дробь, где Pm(x)
и
- нек.рац.дробь, где Pm(x)
и
 )
– многочлены нд полем действ.чисел.
Если
)
– многочлены нд полем действ.чисел.
Если
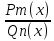 - непрерыв.дробь, т.е. degPm(x)
- непрерыв.дробь, т.е. degPm(x)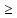 deg
deg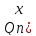 ),
тогда приводим её к виду
),
тогда приводим её к виду
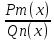 =W(x)+
=W(x)+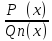 ,
где W(x)
и
,
где W(x)
и
 -
мн-ны над R,
причем рац.дробь
-
мн-ны над R,
причем рац.дробь
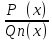 - явл.правой, т.е. deg
- явл.правой, т.е. deg < deg
< deg
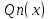 .
Теорема. Пусть Qn(x)=Qn(x-x1)a1(x-x2)a2…(x-xm)am
*(x2+p1x+q1)b1(x2+p2x+q2)b2…(x2+pkx+qk)bk
и
рац.дробь
.
Теорема. Пусть Qn(x)=Qn(x-x1)a1(x-x2)a2…(x-xm)am
*(x2+p1x+q1)b1(x2+p2x+q2)b2…(x2+pkx+qk)bk
и
рац.дробь
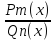 – правая, тогда имеет место след.разложение.
– правая, тогда имеет место след.разложение.
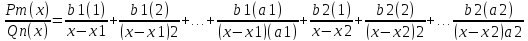 +…+
+…+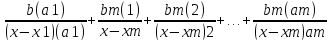 +…
после того,как люб.рац.дробь разложили
по предыдущ.теореме, получаем след.случай:
(1)
+…
после того,как люб.рац.дробь разложили
по предыдущ.теореме, получаем след.случай:
(1)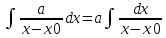 =a
ln(x-x0)+C.
(2)
=a
ln(x-x0)+C.
(2)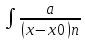 dx=
dx=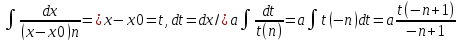 =
=

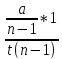 +C=
+C=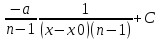 (3)
(3)
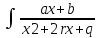 dx=
dx=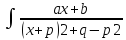 dx=\
x+p=t,
dt=dx\=
dx=\
x+p=t,
dt=dx\=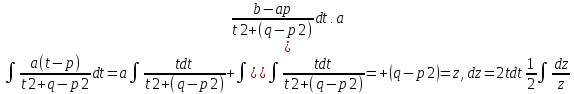 =
=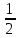 ln|z|+C=
ln|z|+C= ln|t2+(q-p2)|+C.
ln|t2+(q-p2)|+C.
Билет
18.Основные
свойства определенного интеграла.
Оценки интегралов.
1.

 2.Каковы бы ни были точки a,b
и c:
2.Каковы бы ни были точки a,b
и c:
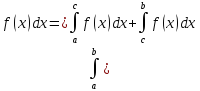 3.k-нект.число.
Тогда
3.k-нект.число.
Тогда
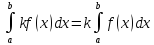 4.
4.
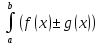 dx=
dx=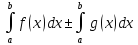 4’Св-во линейности:
4’Св-во линейности:
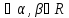
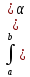 f(x)+
f(x)+ =
=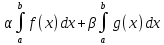 .
Оценки:1 пусть на [a,b]f
(x)
.
Оценки:1 пусть на [a,b]f
(x)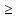 0.тогда
0.тогда
 0.
2пусть f(x)
0.
2пусть f(x) g(x)
g(x)
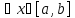 .
Тогда
.
Тогда
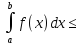
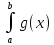 dx.
3пусть m-min
знач.f(x)
на [ab].
m=
dx.
3пусть m-min
знач.f(x)
на [ab].
m=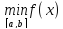 и M-max
знач f(x)
на [ab].Тогда
m(b-a)
и M-max
знач f(x)
на [ab].Тогда
m(b-a)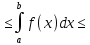 M(b-a).
4|
M(b-a).
4|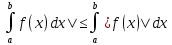 .
5Теорема о среднем. Пусть f(x)
.
5Теорема о среднем. Пусть f(x)
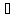 С[ab].Тогда
найдется такая с из [ab],
что
С[ab].Тогда
найдется такая с из [ab],
что
 f(c)*(b-a).
f(c)*(b-a).
Билет
19.Определенный
интеграл с переменным верхним пределом.
Теорема.
Пусть f(x)-интегрируема
на [ab].
Опр. Ф-ция Ф(х)=.
 – интегр.с переменным верхним пределом.
Теор.пусть ф-ция f(x)
– интегр.с переменным верхним пределом.
Теор.пусть ф-ция f(x)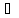 С[ab].
Тогда
С[ab].
Тогда
 Ф'(x)=f(x).
Док-во:фиксир. х из
Ф'(x)=f(x).
Док-во:фиксир. х из
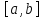 и пусть x+
и пусть x+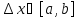 .Тогда
Ф(x+
.Тогда
Ф(x+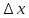 )=
)=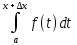 =
=
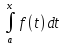 +
+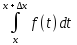 =Ф(x+
=Ф(x+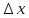 )+
)+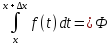 (x+
(x+ )-Ф(х)=
)-Ф(х)= .
Тк ф-ция f(x)
.
Тк ф-ция f(x)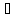 С
С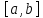 => по теореме о среднем найдется такая
т.с
=> по теореме о среднем найдется такая
т.с
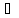 [x,
x+
[x,
x+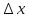 ],
что
],
что
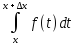 =f(c)
=f(c)
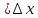 =>
=>
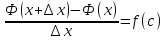 при
при
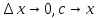 ,
а тк ф-ция непрер., то
,
а тк ф-ция непрер., то
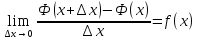 .
.
Существование
первообразной для непрерывной на отрезке
функции.
Следствие1. Если f(x)=c ,
то на дан.отрезке дан.ф-ция имеет
первообразную.
,
то на дан.отрезке дан.ф-ция имеет
первообразную.
Билет 20. Формула Ньютона-Лейбница.
Теорема.
Пусть f(x)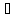 С
[ab]
ипусть F(x)
– одна из первообразных ф-ции f(x).Тогда
С
[ab]
ипусть F(x)
– одна из первообразных ф-ции f(x).Тогда
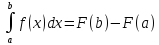 .
.
Замена переменной в определенном интеграле.
Пусть
f(x) С[ab]
и пусть
С[ab]
и пусть
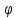 (t)
(t)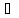 С
и D
[ab],
причем: 1)
С
и D
[ab],
причем: 1)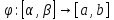 2)
2)
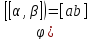 3)
3) =a,
=a,
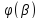 =b.Тогда
=b.Тогда
 док-во: по формуле Н-Л
док-во: по формуле Н-Л
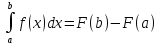 ,
где F(x)
– одна из первообразных ф-ции
f(x).Рассмотрим
ф-цию F(
,
где F(x)
– одна из первообразных ф-ции
f(x).Рассмотрим
ф-цию F(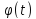 ).
(F(
).
(F(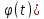 )’=F’(
)’=F’(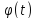 )*
)*
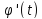 =f(
=f( )*
)*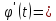 F(
F(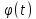 )-
первообр.ф-ции f(
)-
первообр.ф-ции f(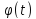 )*
)*
 =>
по формуле Н-Л:
=>
по формуле Н-Л:
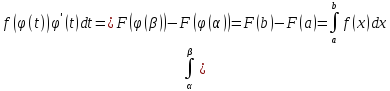 .
Формула
интегрирования по частям в определенном
интеграле. Теорема.Пусть
ф-ции
.
Формула
интегрирования по частям в определенном
интеграле. Теорема.Пусть
ф-ции
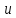 (x)
и
(x)
и
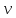 (x)
(x) С,D
[ab].
Тогда
С,D
[ab].
Тогда
 =
=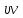 |ab
|ab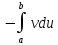 .
Док-во:d(u
.
Док-во:d(u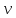 )=ud
)=ud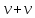 du.
du.

 v|
ab=u(b)
v|
ab=u(b)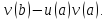
Билет
21.Геометрические
приложения определенного интеграла.
площадь криволинейной трапеции:пусть
f(x)-
опеределена на [ab],
не отриц-на.f(x) [ab].Тогда
S=
[ab].Тогда
S=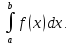 длина дуги кривой:пусть
f(x)
длина дуги кривой:пусть
f(x)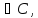 D
[ab].
L=
D
[ab].
L= .
объем тела вращения:
f(x)
.
объем тела вращения:
f(x) [ab].
V=
[ab].
V=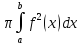 .
площадь
поверхности вращения: f(x)
.
площадь
поверхности вращения: f(x) [ab]
и f
‘(x)
[ab]
и f
‘(x) С[ab].
S=2
С[ab].
S=2 .
.
Билет
22.Несобственные
интегралы 1-го и 2-го рода. Опр.
Пусть f(x)опр-на
на пром-ке[a,+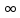 ]
и интегрир-ма в люб.его части [a,R](т.е.
]
и интегрир-ма в люб.его части [a,R](т.е.
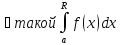 ).
Тогда если
).
Тогда если
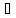
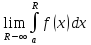 ,
то он наз.неопред. интег-ом 1го рода и
обознач
,
то он наз.неопред. интег-ом 1го рода и
обознач
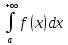 .
Опр. Пусть f(x)
опр-на на проме-ке [ab)
и f(x)
не ограничена в люб.точке окр-ти точка
b,
но
.
Опр. Пусть f(x)
опр-на на проме-ке [ab)
и f(x)
не ограничена в люб.точке окр-ти точка
b,
но
 >0
ф-ция f(x)
интегр-ма на отрезке[a,b-
>0
ф-ция f(x)
интегр-ма на отрезке[a,b- ]
, тогда если
]
, тогда если
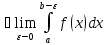 то он наз-ся несобственным интергралом
2го рода. Признак
сходимости несобственных интегралов.
Теорема.
Пусть f(x)
и g(x)определены
и С [a,+
то он наз-ся несобственным интергралом
2го рода. Признак
сходимости несобственных интегралов.
Теорема.
Пусть f(x)
и g(x)определены
и С [a,+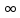 ],
причем 0
],
причем 0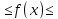 g(x)
на [a,+
g(x)
на [a,+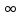 ].
Тогда из сходимости интег-а
].
Тогда из сходимости интег-а
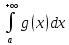 будет
следовать сходимость
будет
следовать сходимость
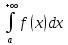 ,
а из расходимости
,
а из расходимости
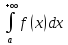 будет
следовать расходимость
будет
следовать расходимость
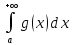 .
.
Билет
23.Функции двух переменных: определение
и основные понятия.
Опр. Пусть x,y,z
– нек.множ-ва(больш). ф-ция 2х переменных
наз множ-во всех таких точек (x,y,z),
что x
 X,
y
X,
y ,
z
,
z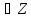 и кажд.пара (x,y)входит
в одну и только одну тройку. В этом случае
говорят, что кжд.паре (x,y)поставлена
в соответствие нек.число z:
z=f(x,y),
при этом z-наз-ся
зависимой переменной, а x
и y-
незваис. Мн-ва всех пар (x,y)
наз.областью опр-я ф-ции f,
а мн-ва всех знач-й z
наз. обл-ю значений ф-ции f.
Введем на пл-ть Оxy
метрику
и кажд.пара (x,y)входит
в одну и только одну тройку. В этом случае
говорят, что кжд.паре (x,y)поставлена
в соответствие нек.число z:
z=f(x,y),
при этом z-наз-ся
зависимой переменной, а x
и y-
незваис. Мн-ва всех пар (x,y)
наз.областью опр-я ф-ции f,
а мн-ва всех знач-й z
наз. обл-ю значений ф-ции f.
Введем на пл-ть Оxy
метрику
 .
Пусть М1(x1y1)
М2(x2y2).
.
Пусть М1(x1y1)
М2(x2y2).
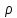 (М1М2)=
(М1М2)=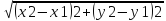
Опр.
-окрестность. Точки М0(x0y0)
наз. Такое мн-во точек пл-ки Oxy,
д/кот выпол.нер-во:
 <
<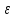 :
U
:
U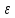 (M0)={M
(M0)={M (M0M)<
(M0M)<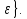 Опр.
Пусть имеется послед-ть точек М1(x1y1),
M2(x2y2)…Mn(xn,yn)
({Mn}
n
Опр.
Пусть имеется послед-ть точек М1(x1y1),
M2(x2y2)…Mn(xn,yn)
({Mn}
n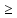 1).
Последовательность Mn
наз сходящейся к точке М0(x0y0),если
1).
Последовательность Mn
наз сходящейся к точке М0(x0y0),если
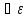 >0
найдется такой номер N,
зависящий N(
>0
найдется такой номер N,
зависящий N(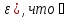 n>N
будет вып-ся:
n>N
будет вып-ся:
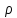 (M0,Mn)<
(M0,Mn)< .
Предел
функции двух переменных и его свойства.
Пусть
f(xy)опр-на
на нек мн-ве {M}
.
Предел
функции двух переменных и его свойства.
Пусть
f(xy)опр-на
на нек мн-ве {M}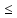 R*R
и пусть М0-нек.точка плоскости. Число А
наз пределом ф-ци f(xy)
в точке М0, если
R*R
и пусть М0-нек.точка плоскости. Число А
наз пределом ф-ци f(xy)
в точке М0, если
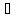 {M}n
{M}n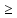 1
1
 {M}},
причем Mn
{M}},
причем Mn M0,
и Mn->n->
M0,
и Mn->n->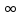 M0,
то
M0,
то
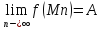 .
Опр. Число А наз пределом f(xy)
в т М0, если
.
Опр. Число А наз пределом f(xy)
в т М0, если
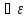 >0
>0
 s=S(
s=S(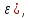 что
что
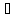 M
M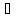 {M}
с усл 0<f(M0,M)<s=>
условие |f(M)-A|<
{M}
с усл 0<f(M0,M)<s=>
условие |f(M)-A|<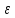 .
С-ва: Теор. Пусть f(xy)и
g(xy)
опр-ны на мн-ве {M}
и пусть сущ-ют пределы:
.
С-ва: Теор. Пусть f(xy)и
g(xy)
опр-ны на мн-ве {M}
и пусть сущ-ют пределы: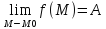 и
и
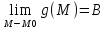 .
Тогда 1.
.
Тогда 1.
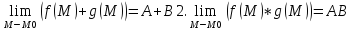 3.
Если В
3.
Если В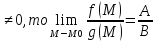
Билет 28.Производная по направлению. Градиент.
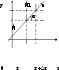
Пусть ф-ия z=f(M) определена в нек-ой окрестности т. M(x,y) и задан единичный вектор n=(cos,cos). Для хар-ки скорос-ти изменения ф-ии в т. M(x,y) введем понятие произ-ой по направлению n. Для этого проведем через т. M(x,y) прямую так, чтобы одно из направлений на ней совпадало с направл-ем вектора n. Возьмем на этой прямой т.М1(x+x,y+y).
Обозначим
длину L=|MM1|=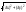 .
.
Опр.
Производная f(xy)
по направлению n
в точке М наз.след предел:
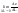 =
f‘x(x,y)cos+
f‘y(x,y)cos=
=
f‘x(x,y)cos+
f‘y(x,y)cos= .
Пусть f(xy)
диф-ма в т. М. Тогда
.
Пусть f(xy)
диф-ма в т. М. Тогда
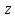 = f‘x(x,y)x+f‘y(x,y)y
+ (x,y)x+(x,y)y,
где x
= Lcos,
y
= Lcos
= f‘x(x,y)x+f‘y(x,y)y
+ (x,y)x+(x,y)y,
где x
= Lcos,
y
= Lcos
Разделим
обе части нерав-ва на L.
z/L=f‘x(x,y)cos+f‘y(x,y)cos+
(x,y)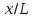 +(x,y)
+(x,y) .
Перейдем
в последнем равенстве к пределу при
L0.
.
Перейдем
в последнем равенстве к пределу при
L0.
Градиент.Опр.: Град-том ф-ии z=f(M) в т. M(x,y) наз-ся вектор, координаты кот-го равны соответс-им частным произ-водным в т. M(x,y). gradz=(z/x,z/y). Используя опр-ие grad м. получить след. формулу для производной по напр-ию.z/L=f‘x(x,y)cos+f‘y(x,y)cos, L=(cos,cos), z/L= grad z·L=grad z·L cos, z/L= grad z ·cos Градиент ф-ии z=f (x, y) в т. M (x,y) хар-ет направление и величину max-ой скорости изменения и возрастания ф-ии в данной точке.
Билет
30.Экстремумы функций двух переменных.
Необходимое условие экстремума.
Достаточное условие экстремума.
Пусть ф-ция
x=f(xy)
определена на нек множевстве {М}. Опр.:
т.М0(x0,y0)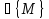 наз-ся точкой лок.max(min),
если найдется такая окрестность U(M0),что
для люб.т М
наз-ся точкой лок.max(min),
если найдется такая окрестность U(M0),что
для люб.т М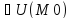 значение ф-ции f(М)
значение ф-ции f(М)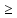 f(М0),
(f(М)
f(М0),
(f(М)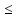 f(М0)).
Т(необ-ое
условие экстремума):
Если ф-ия z=f(x,y)
в точке М0(x0,y0)
имеет экст-ремум, то обе частные
производные в этой точке равны нулю.
Опр.:
Точки, в к-ых обе частные производные
равны нулю, наз-ся стационарными точками.
f(М0)).
Т(необ-ое
условие экстремума):
Если ф-ия z=f(x,y)
в точке М0(x0,y0)
имеет экст-ремум, то обе частные
производные в этой точке равны нулю.
Опр.:
Точки, в к-ых обе частные производные
равны нулю, наз-ся стационарными точками.
Т(достаточное
условие экстремума):
Пусть ф-ция z=f(xy)
определена в нек.окр.
 в т М0 и пусть в дан.точке
в т М0 и пусть в дан.точке
 частн.произв-е 1го порядка=0. Пусть в дан
окр-ти
частн.произв-е 1го порядка=0. Пусть в дан
окр-ти
 непрерывные частные производные 2го
порядка. Рассмотрим величину
непрерывные частные производные 2го
порядка. Рассмотрим величину
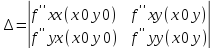
35.Дифференциальные уравнения: основные понятия и определения.
Опр.:
Ур-ие вида f(x,y,y’)=0
(1)
наз-ся диф-ым ур-ем 1-го порядка, где x
– перем-я, y–иско-мая
ф-я, y’
– ее производная.Опр.:
Поряд-ком
диф-го ур-ия наз-ся порядок старшей
производной, входящей в него. Если ур-ие
(1) можно решить относительно y’,
то оно примет вид: y’=f
(x,y)
(2),
к-ое наз-ют диф-ым
ур-ем, разрешенным относитель-но произ-ой.
Опр. Решение ур-я (2) наз всякая ф-ция
y= ,кот.при
подстановке в ур-е(2) обращает его в
тождество, те
,кот.при
подстановке в ур-е(2) обращает его в
тождество, те
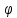 ’(x)
’(x)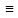 f(x,
f(x,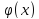 )
Опр. График решения диф-ого ур-я (2) наз
интегральн.кривой. Опр. Диф.ур-е y’=f(xy)с
задан. начальн. условиями.
)
Опр. График решения диф-ого ур-я (2) наз
интегральн.кривой. Опр. Диф.ур-е y’=f(xy)с
задан. начальн. условиями.
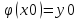 наз. Задачей Коши.
наз. Задачей Коши.
С
геометр-ой точки зрения задача Коши
озна-чает, что из множества интегральных
кривых области G
мы должны выбрать одну, проходящую через
данную точку (х0,у0).
Теорема.
Пусть ф-ция f(xy)
непрер в нек. обл. G
и
 такая
константа L,
что для люб пары точек (x,y1),
(x,y2)
такая
константа L,
что для люб пары точек (x,y1),
(x,y2)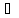 G
следует, что |f(x,y1)-f(x,y2)|
G
следует, что |f(x,y1)-f(x,y2)|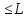 *|y1-y2|
- ур-е Лепшиц.
*|y1-y2|
- ур-е Лепшиц.
Общее
и частное решение диф-го ур-ия. Опр.:
Общим решением
ур-ия (2) в области G
наз-ся ф-ия y=(x,C),
зависящая от неизвестной x
и произвольной постоянной С, такая, что
 С=С0 –фция (x,C)
явл-ся решением ур-я (2) и
С=С0 –фция (x,C)
явл-ся решением ур-я (2) и
 (x0y0)
(x0y0)
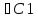
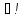 С=С1, такая что U(x,C0)
яв-ся решением задачи Коши.Опр.:
Частным
решением ур-я
(2) наз-ся ф-ия y=(x,C0),
полученная из общего решения ур-я(1)
заменой постоянной с определенным
значением. С гео-метр-ой точки зрения
частному решению соответствует одна
интегральная кривая, а общему – семейство
интегральных кри-вых.
С=С1, такая что U(x,C0)
яв-ся решением задачи Коши.Опр.:
Частным
решением ур-я
(2) наз-ся ф-ия y=(x,C0),
полученная из общего решения ур-я(1)
заменой постоянной с определенным
значением. С гео-метр-ой точки зрения
частному решению соответствует одна
интегральная кривая, а общему – семейство
интегральных кри-вых.
36.Дифференциальные уравнения с разделяющимися переменными.
Опр.: Ур-ие вида y’=f(x) g(y) наз-ся диф-ым ур-ем с разделяющимися переменны-ми, где f(x) и g(y) – непрерывные ф-ии. Чтобы решить такое ур-ие нужно разде-лить переменные, т.е. в левой части соб-рать все y, в правой – x. Для этого: 1. за-менить y’ на dy/dx; 2. умножить обе части на dx и разделить обе части на g(y) (g(y)0)
1) dy/dx = f(x)·g(y) ; dy/ g(y) + C1= f(x)dx + C2
2) dy/g(y) = f(x)dx ; dy/g (y) = f(x)dx + C2-C1 (C2-C1=C).
Однородные ур-ия. Опр.: Ур-ие y’= f(x, y) наз-ся однородным, если ф-я f(x,y) м. б. представлена как ф-я отношения своих аргументов. Схема решения: 1). обозначить y/x=U, y=Ux; 2). y’=U’x+U; 3) подставить y и y’ в данное ур-ие, решить его относительно ф-ии U; 4) сделать обратную замену, т.е. U выразить через x и y.
39. Лин. однородные диф. ур. второго порядка с пост. коэф. Однород.ур-я.(ОУ)
Опр.
Линейн.ОУ диф-ные ур-я 2 порядка, с
пост.коэф.наз-я ур-е вида

Опр.характеристич.ур-ем
соответствующим ур-ю (1), наз-ся ур-е
вида:
Т1:
Пусть k0-корень
хар-рного ур-я(2), кот соотв. Ур-ю (1). Тогда
ф-ция

Д-во:
имеем
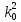 +pk0+q=0,
подставляем
+pk0+q=0,
подставляем
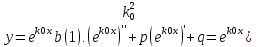 +pk0+q)=0
+pk0+q)=0
Т2:Пусть к1,к2-корни хар-ного ур-я(2)
Возможны случаи:
1.Если
к1,к2 и к1
и к1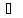 к2,
тогда общ.реш-е ур-я (1)выглядит след.
Образом:
к2,
тогда общ.реш-е ур-я (1)выглядит след.
Образом:
2.
к1,к2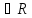 ,
к1=к2=к. Общее реш-е ур-я(1):
,
к1=к2=к. Общее реш-е ур-я(1):
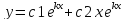
Док-во:
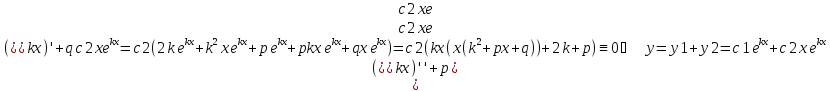
3.Если
к1 и к2- комплексные, тогда к1 и к2-сопряженные:
к1=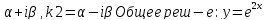 (c1
(c1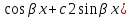
38.Дифференциальные уравнения второго порядка, допускающие понижения порядка.
Опр:
ур-е вида F(x,y,y’,y’’)=0,
где х- независимая переменная, у- искомая
фун-я, y’,y’’- ее производные, назыв диф
ур-ем 2-го порядка. Обычно расматр-ся
ур-я, кот. могут быть разрешены от-но
y’’, т.е. ур-е вида: y’’=f(x,y,y’) (1) Опр:
решением ур-я (1) назыв-ся фун-я y= (x),кот.
обращает его в тождество
(x),кот.
обращает его в тождество
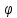 ’’(x)
’’(x)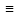 f(x,
f(x, .
Теорема (Коши):
.
Теорема (Коши):
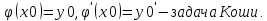 Общ.решение
ДУ(1): ф-я у=φ(х1,С1,С2) зависящая от х и 2-х
произвольных постоянных С1,С2, назыв
общим решением ур-я (1). Если она яв-ся
решением ур-я (1) при люб-х значениях
С1,С2 и если при начал-х условиях сущ-т
единственные значения постоянных С1=С1º
,С2=С2º, такие что ф-я у=φ(х,С1º,С2º)
удовлетворяет нач-м условиям. Опр: любая
ф-я у=φ(х,С1º,С2º) полученная из общего
решения ур-я (1) при опред-х значениях
постоянных С1 и С2 назыв частным
решением
ур-я (1). Рассм.
3 случая когда решение ур-я (1) с помощью
замены переменной сводится к решению
ур-я 1-ого порядка. Такое преобразование
ур-я назыв. понижением
порядка.
1.Ур-е
вида у’’=f
(х)
(нет у, у’), введем новую ф-цию z (x)=y, y’’=z
(x), подставим в ур-е y’’ получим ур-е
1-ого порядка решив к-ое найдем ф-цию z
(x) а значит нашли у' и теперь решая ур-е
для у’ найдем искомую ф-цию у. y’=x.
2.Ур-е
вида y’’=f
(x,
y’)
(нет у) введем вспомогательную ф-цию z
(x)=y’,
тогда y’’=z
(x)
подставив все в данное ур-е получим ур-е
1-ого порядка, решив к-ое найдем ф-цию z
(x),
т.е. y’
и решая ещё раз ур-е найдем искомую ф-цию
y’.
3.Ур-е
вида y’’=f
(y,
y’)
введем вспомогательную ф-цию z
(y)
так что y’=z.
y’’
= z
dz/dy.
Подставим в данное ур-е y’’
и y’
и решив его найдем z,
т.е. y’
и решив ур-е для y’
найдем y.
Общ.решение
ДУ(1): ф-я у=φ(х1,С1,С2) зависящая от х и 2-х
произвольных постоянных С1,С2, назыв
общим решением ур-я (1). Если она яв-ся
решением ур-я (1) при люб-х значениях
С1,С2 и если при начал-х условиях сущ-т
единственные значения постоянных С1=С1º
,С2=С2º, такие что ф-я у=φ(х,С1º,С2º)
удовлетворяет нач-м условиям. Опр: любая
ф-я у=φ(х,С1º,С2º) полученная из общего
решения ур-я (1) при опред-х значениях
постоянных С1 и С2 назыв частным
решением
ур-я (1). Рассм.
3 случая когда решение ур-я (1) с помощью
замены переменной сводится к решению
ур-я 1-ого порядка. Такое преобразование
ур-я назыв. понижением
порядка.
1.Ур-е
вида у’’=f
(х)
(нет у, у’), введем новую ф-цию z (x)=y, y’’=z
(x), подставим в ур-е y’’ получим ур-е
1-ого порядка решив к-ое найдем ф-цию z
(x) а значит нашли у' и теперь решая ур-е
для у’ найдем искомую ф-цию у. y’=x.
2.Ур-е
вида y’’=f
(x,
y’)
(нет у) введем вспомогательную ф-цию z
(x)=y’,
тогда y’’=z
(x)
подставив все в данное ур-е получим ур-е
1-ого порядка, решив к-ое найдем ф-цию z
(x),
т.е. y’
и решая ещё раз ур-е найдем искомую ф-цию
y’.
3.Ур-е
вида y’’=f
(y,
y’)
введем вспомогательную ф-цию z
(y)
так что y’=z.
y’’
= z
dz/dy.
Подставим в данное ур-е y’’
и y’
и решив его найдем z,
т.е. y’
и решив ур-е для y’
найдем y.
