Razdatochnyy_material_2010

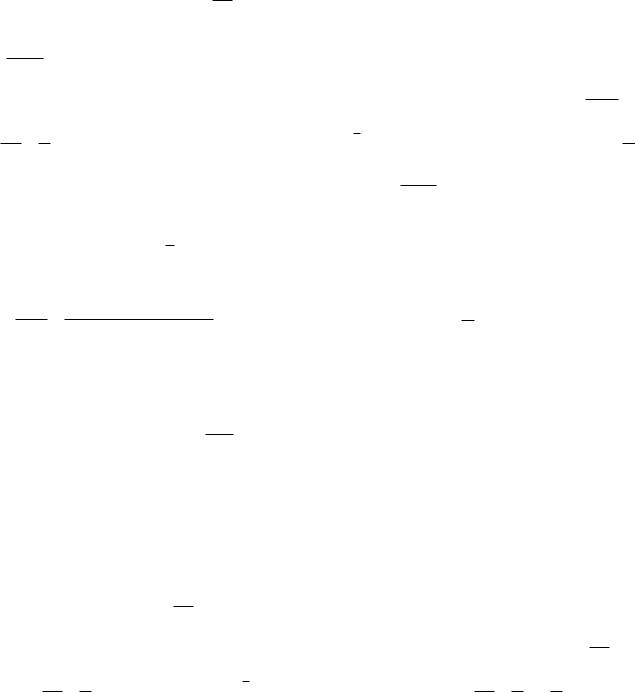
11. Динамические модели макроэкономики. Линейные модели динамики валового внутреннего продукта (ВВП) и чистого внутреннего продукта (ЧВП): простая модель, модель Харрода-Домара.

Справедливо основное макроэкономическое тождество Y = I + C, где C конечное потребление;инвестиции в накопление ОПФ, Y – чистый внутр. продукт (ЧВП), причем Y X (1 am ) , где Х – ВВП, a

	норма отчислений на амортизацию. I B			dY	- линейный акселератор, где В капиталоемкость ЧВП.
				dt
	Подставим в основное макроэк. тождество выражение для инвестиций, получим (*)
	Y (t) B	dY (t)	C(t) однопродуктовая динамическая модель ЧВП Леонтьева.
		dt
	Случай 1. C(t) 0 предельный случай, то есть, потребления нет. Уравнение примет вид Y(t)= B					dY(t)
						dt

I

m

,

отсюда

	dY		1	Y
	dt		B

1 t

. Решение уравнения имеет вид Y (t) Y (0)eВ , то есть Y (t) растет с индексом

IndY

1 В

.

Случай 2:

C(t) C(0) const

. Уравнение модели имеет вид

Y (t)

	B	dY (t)
		dt

C(0)

, где

B

const

. Запишем:

1

t – общее решение однородного

Y * (t) = C(0) – частное решение неоднородного уравнения, Y

(t) C e

В

1

уравнения. Далее запишем Y (t) Y (t) Y *(t) C1e

t

C(0) – общее решение неоднородного уравнения. При

t 0 получим Y (0) C1 C(0) откуда C1 Y (0) C(0) , Y (t) Y (0) C(0) e

t

C(0) .

Y

(t)

e t

1

IndY (t)

Y (0) C(0)

темп прироста дохода, он стремится к

при t + .

Y (t)

Y (0) C(0) e

t

C(0)

B

Модель чистого внутреннего продукта Харрода-Домара

Совместное действие мультипликатора

1

и акселератора B порождает непрерывный и прогрессирующий

c

1

рост выпуска продукции или дохода. Y = I + C + A основное балансовое соотношение, где I Ia Ii

сумма

интенсивностей автономных инвестиций вместе с индуцированными инвестициями, причем I

B

dY

,

i

dt

C Ca Ci

сумма интенсивностей автономного потребления вместе с индуцированным потреблением, Ci kY

норма потребления постоянна (для части потребления, зависящего от ЧВП), A

сумма интенсивностей чистого

экспорта Ex

и государственных закупок Gv .

В итоге получаем уравнение Y B

dY

kY Ia

Ca Ex Gv модель Харрода-Домара. Обозначим

dt

A Ia Ca Ex Gv . Введем s 1 k

норма производственного накопления. Отсюда sY B

dY

dt

dY

s

s

t

dY

dY

s

A

A 0 , имеем dt

B Y , откуда Y (t) Y (0)e

B

. В общем случае sY B dt A ,

dt

B y B .

Анализ модели проводится аналогично в трех основных случаях: А = 0, А = А(0), А = А(0) ert.

A

. При

12. Линейная односекторная модель динамики ВВП.

Рассмотрим линейную односекторную модель выпуска валового внутреннего продукта (ВВП) с учетом выбытия (амортизацией) с инерционным запаздыванием фондообразованием.

X(t) – ВВП, A(t) – внешние инвестиции, I(t) – собственные инвестиции,

V(t) –инвестиции в производство,

F(t) – основные произв. фонды (ОПФ), C(t) –непроизводственное потребление,

– средняя капиталоотдача,

а– ср. норматив отчислений на кап. вложения, n – ср. норма амортизации ОПФ, Т – лаг фондообразования.

Справедливо: X ( p) W ( p) A( p)

, W ( p)

( p)

2

( p)

3

( p)

1

, W ( p)

, модель

2

c

c

1

( p)

( p)

(t)F ( p)

c

Tp

(Tn 1) p n a

2

1

3

d

2

X

dX

имеет вид:

T

(Tn 1)

(n a ) X A(t) .

dt

2

dt

Характ. ур-ие имеет вид:

T

2

(Tn 1) n a 0

Ее корни: 1,2

Tn 1

1

(Tn 1)

2

4T (n a )

2T

2T

Tn 1

1

(Tn 1)

2

4a T

. Корни вещественные. Соответственно выводим: условие n a

означает, что

2T

2T

1,2 0

, то есть в ситуации отсутствия автономных инвестиции ( A(t) 0 ) ВВП X (t) сокращается, условие

n a

означает, что 2

0 ,

а 1

0

, то есть в ситуации отсутствия автономных инвестиции ВВП

X (t)

растет.

И, наконец, в ситуации маловероятной

n a

находим

1 0

и

2

(n

1 T

)

. В этом случае в ситуации

отсутствия автономных инвестиции выпуск стабилизируется.

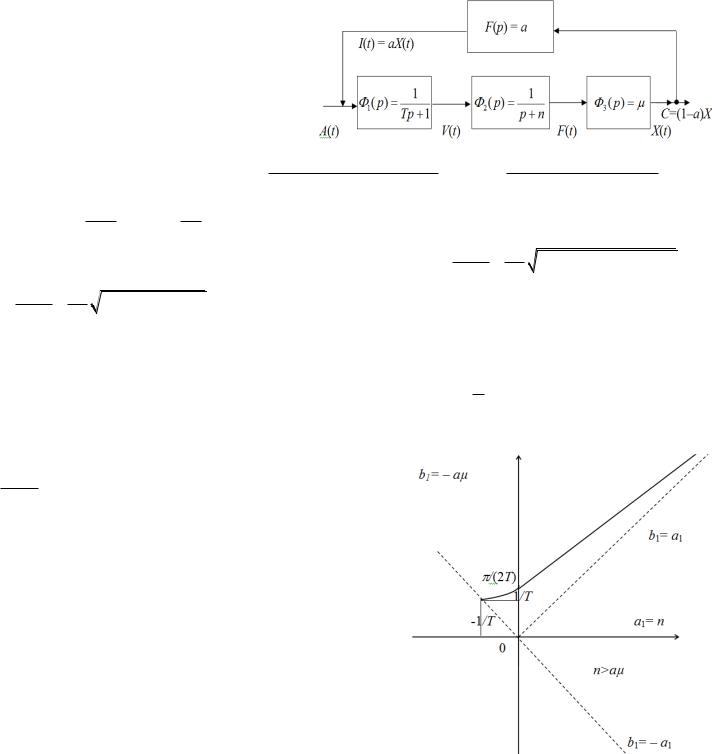
Модель выпуска ВВП с учетом выбытия (амортизации) и с дискретным запаздыванием образования капитала имеет вид:

dX (t)		nX (t) a X (t T ) A(t T ), t 0,
	dt
X ( ) X			0	( ), если 0.
По графику видно, что условие n a					означает, что

асимптотическая устойчивость, то есть в ситуации отсутствия

автономных инвестиции ( A(t) 0 ) ВВП

X (t) сокращается,

условие n a означает, что имеет место неустойчивость, то есть в ситуации отсутствия автономных инвестиции ВВП X (t) растет. И, наконец, в ситуации n a находим, что в этом

случае в ситуации отсутствия автономных инвестиции выпуск стабилизируется, то есть уравнение просто устойчиво.

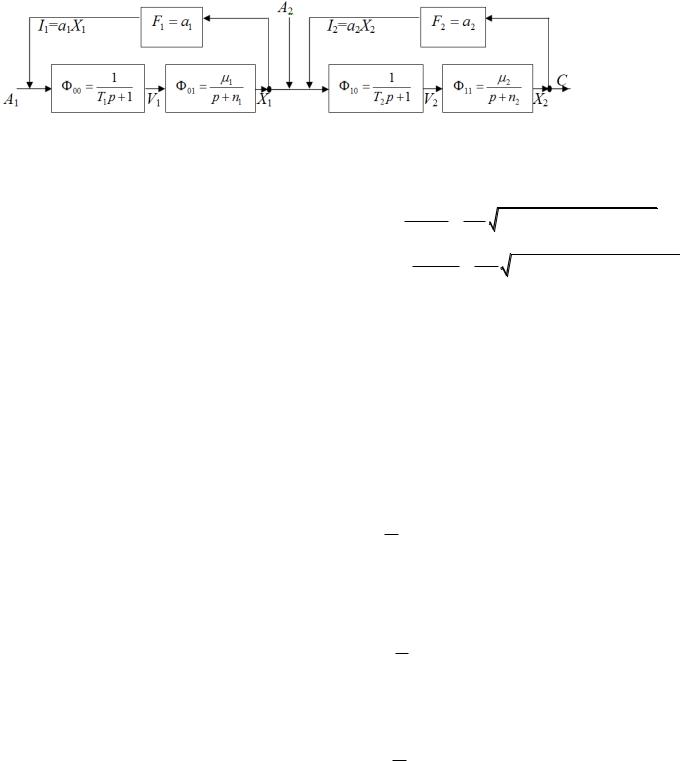
13.Линейная двухсекторная модель динамики ВВП.

X i – валовые выпуски секторов, i 1, 2, Ai – автономные инвестиции секторов, Ii – внутренние инвестиции секторов, Vi – реальные инвестиции в производство в секторах, i – средние технологические темпы (фондоотдачи) секторов, ai – средний норматив отчислений на капитальные вложения, ni – средняя норма амортизаций ОПФ, Ti – средний лаг фондообразования, причем X1 W1 A1 , X2 W2 ((1 а1 )X1 A2 ) ,

С (1 a2 )X2 .

Модель имеет вид:
T	d 2 X1	(T n 1)		dX1	(n a ) X				A ,		T	d 2 X 2	(T n 1)		dX 2	(n a			) X			((1 а ) X		A ) ,
								1												2			1
1	dt	1	1	dt	1	1	1		1	1	2		2	2	dt	2	2	2			2	1		2
												dt

C (1 a2 )X2 .

Первое характ. ур-ие:

T	2	(T n 1) n a
1		1	1	1	1	1

0

,

		T n 1			1	(T n		1)	2	4T (n a )
		1	1
1,2			2T		2T	1	1			1	1	1	1
			1		1

.

T2

2

(T2n2 1) n2 a2 2 0 ,

3,4

T n

1

1

1)

2

4T2

(n2 a2 2 ) .

Второе характ. ур-ие:

2

2

(T2n2

2T

2T

2

2

Условие n1

a1 1 , n2

a2 2 означает,

что корни первого характ. уравнения 1,2

0

и корни второго характ.

уравнения

3,4 0 , то есть, в ситуации отсутствия автономных инвестиции ( A1

(t) 0

, A2 (t) 0 ) выпуски X1 (t)

и

X 2 (t) сокращается. Условие n1

a1 1 , n2 a2 2 означает,

что 2

0 , а

1 0

, в то время как 3,4 0 . То есть,

в ситуации отсутствия автономных инвестиции выпуск

X1 (t)

растет, а выпуск

X

2 (t)

стремится к тренду,

определяемому выпуском

X1 (t) . Условие n1 a1 1 , n2

a2 2

означает, что 2,4

0 . То есть, в ситуации

отсутствия автономных инвестиции выпуск X1 (t) растет, а выпуск

X 2 (t) тоже растет. Условие

n1 a1 1 ,

n2

a2 2 означает, что корни первого характ.уравнения 1,2 0

и корни второго характ. уравнения

4 0 ,

3

0 . То есть, в ситуации отсутствия автономных инвестиции ( A1 (t) 0 ,

A2 (t) 0 ) выпуск X1 (t)

сокращается,

в то время как выпуск

X 2

(t) растет.

Наконец, в ситуации n1 a1 1 находим

1 0 и 2 (n1

1

) . В этом случае, в ситуации отсутствия

T

1

автономных инвестиции, выпуск

X1 (t)

стабилизируется. Условие n2

a2 2 означает, что корни второго

характеристическое уравнение 4

0

, 3 0 , значит, выпуск

X

2 (t)

растет. Условие

n2 a2 2

означает, что

корни второго характ. уравнения

3,4

0 , поэтому, хотя выпуск

X1 (t) стабилизируется, выпуск

X 2

(t) падает. И

последнее, в ситуации

n a
1	1	1

находим

1 0

и

2

(n1

		1	)
		T
		1

, а в ситуации

n2 a2 2

находим

3 0

и

	(n		1	) . В этом случае в ситуации отсутствия автономных инвестиции выпуск X															(t) и выпуск X		(t)
																		1		2
4	2		T2
постоянные.
Наконец, в ситуации					n	a			находим 0 и (n				1	) . Условие n a			означает, что корни первого
								2
					2	2			3	4	2		T	1	1	1
													2
характ. уравнения 2					0 , 1		0 , значит, выпуск X1 (t)				растет,			выпуск X 2 (t) тоже растет. Условие n1 a1 1
означает, что корни первого характ. уравнения 1,2										0 , поэтому, хотя выпуск X1 (t)							падает, выпуск X 2 (t)
стабилизируется.

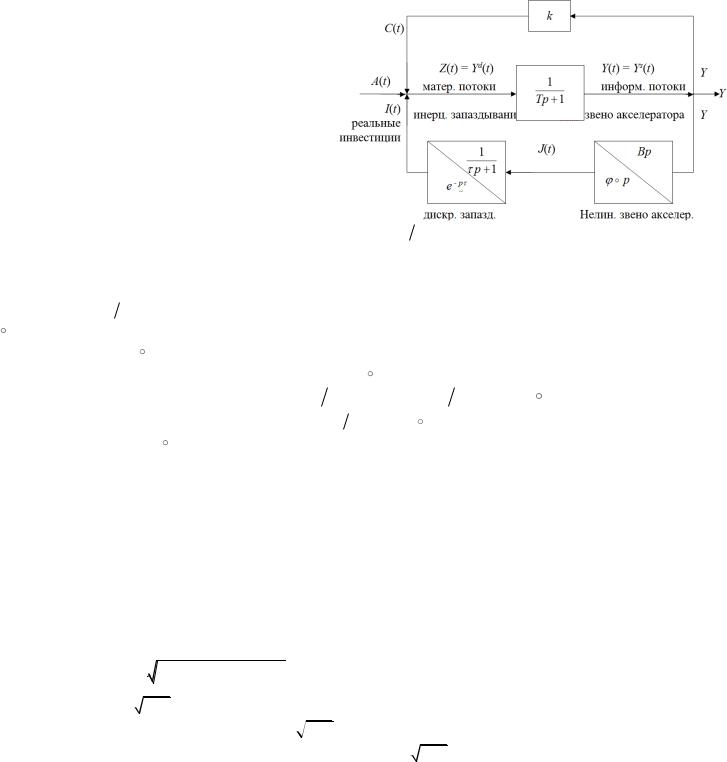
14. Линейная и нелинейная модель Филлипса динамики ВВП, ЧВП, капитала и инвестиций.

I BY

- линейный акселератор (дифференцирующее звено),. Рассматривают также случай нелинейного

, где – одна из указанных ниже функций. Акселератор позволяет по Y

определить

акселератора I (Y )

интенсивность планируемых инвестиций (решений об инвестировании) J (Y ) .

В этой схеме объединены линейный и нелинейный

случаи.

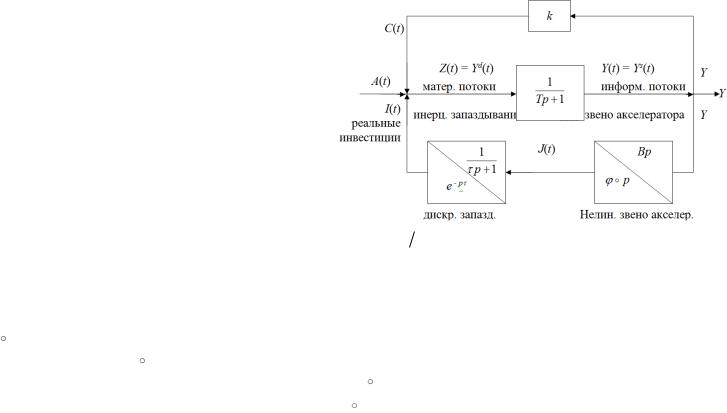
Здесь Z (t) Y

d

(t) — спрос на ЧВП,

Y (t) Y

s

(t)

–

предложение ЧВП.

I

– интенсивность инвестиций, индуцированных

ЧВП, B

– коэффициент акселератора (приростная

капиталоемкость ЧВП),

Y – интенсивность производства ЧВП,

J

- запланированные инвестиции,

k

- предельная склонность к потреблению.

А – автономные инвестиции.

Между спросом и предложением имеется

инерционное запаздывание, то есть зависимость вида

Y ( p) Z( p) (Tp 1) при Y (0) 0 . Это означает, что

между Z и Y существует зависимость в виде ЛОДУ

TY

Y Z . Здесь

T

лаг запаздывания формирования

предложения ЧВП. Далее распишем TY

Y Z A I

C , где C kY

– потребление, индуцированное ЧВП.

Реальные инвестиции

I

связаны с запланированными инвестициями J

инерционным запаздыванием. I

I

J

то есть I ( p) J ( p) ( p 1) при I (0) 0 . Здесь

– лаг запаздывания ввода реальных инвестиций. Выражение

p означает последовательное выполнение двух операций: дифференцирования и вычисления значения

функции. Например, (

p)(Y ( p)) в изображениях означает в оригиналах следующее:

. Отсюда можно

(Y (t))

написать, что в случае нелинейного акселератора J ( p) ( p)(Y ( p))

—

— для изображений, J (t) (Y (t))

для оригиналов. Далее при

I (0) 0 имеем

I ( p) 1

( p 1) J ( p) 1

( p 1)(

p)(Y ( p)) . Выведем

модель Филипса. Перепишем тождество

I ( p) C( p) 1 ( p 1) ( p)(Y ( p)) kY ( p)

в виде

( p 1)(I ( p) C( p))

(

p)(Y ( p)) ( p 1)kY ( p) .

Перейдем к оригиналам (при Y (0) 0 ,

I (0) 0 , C(0) 0 ):

(I (t) C (t)) I (t) C(t)

(Y (t)) k( Y (t) Y (t))

. Далее продифференцируем тождество

TY Y Z A I C ,

получим TY Y Z A I C .

Выразим: I

C

TY

Y

(TY

Y

Y A

kY ,

A , откуда

A ) TY

(Y (t)) k Y

TY (T k )Y

(Y ) (1 k)Y A A . Обозначим

s 1 k

,

получим нелинейную модель Филипса TY

(T s )Y

(Y ) sY A A . Линейный случай возникает,

когда (Y ) BY . Линейная модель Филлипса имеет вид: TY (T s B)Y sY A A.

Линейная модель Филлипса асимптотически устойчива тогда и только тогда, когда T s B 0 .

В случае линейной модели Филлипса все зависит от корней характеристического уравнения

1

B T s

.

1,2

(s T B)2 4 sT

2 sT

,

Если 0 T s B 2 sT , процесс циклический с затухающей амплитудой, то есть линейная модель Филлипса асимптотически устойчива. Если T s B 2 sT , процесс монотонный убывающий, то есть линейная

модель Филлипса асимптотически устойчива. Если T s B 2 sT , процесс монотонный убывающий, то есть линейная модель Филлипса асимптотически устойчива.

15. Линейная и нелинейная модель Гудвина динамики ВВП, ЧВП, капитала и инвестиций.

I BY

- линейный акселератор (дифференцирующее звено),. Рассматривают также случай нелинейного

акселератора

I

определить

(Y ) , где – одна из указанных ниже функций. Акселератор позволяет по Y

интенсивность планируемых инвестиций (решений об инвестировании)

J (Y ) .

В этой схеме объединены линейный и нелинейный

случаи.

Z (t) Y

d

(t)

Здесь

— спрос на ЧВП,

Y (t) Y

s

(t)

–

предложение ЧВП.

I

– интенсивность инвестиций, индуцированных

ЧВП,

B

– коэффициент акселератора (приростная

капиталоемкость ЧВП),

Y

– интенсивность производства ЧВП,

J

- запланированные инвестиции,

k

- предельная склонность к потреблению.

А – автономные инвестиции.

Между спросом и предложением имеется

инерционное запаздывание, то есть зависимость вида Y ( p) Z( p) (Tp 1) при Y (0) 0 . Это означает, что

между Z и Y существует зависимость в виде ЛОДУ TY

Y Z . Здесь T

лаг запаздывания формирования

предложения ЧВП. Далее распишем TY

Y Z A I C , где C kY

– потребление, индуцированное ЧВП.

Реальные инвестиции I

связаны с запланированными инвестициями J

дискретным запаздыванием

I (t) J (t )

, то есть

I ( p) e

p

J ( p) .Здесь – лаг запаздывания ввода реальных инвестиций. Выражение

p

означает последовательное выполнение двух операций: дифференцирования и вычисления значения

функции. Например, (

. Отсюда можно

p)(Y ( p)) в изображениях означает в оригиналах следующее: (Y (t))

написать, что в случае нелинейного акселератора J ( p) (

p)(Y ( p))

—

— для изображений, J (t) (Y (t))

для оригиналов. Далее при

I (0) 0 имеем I ( p) e p ( p)(Y ( p)) .

Выведем модель Гудвина.

TY Y Z A I C , где I (t) (Y (t )) , C(t) kY (t) . Отсюда получим

TY (t) Y (t) A(t) (Y (t )) kY (t) . Итак, получаем следующие уравнения модели:

— нелинейная модель Гудвина (в случае нелинейного акселератора),

TY (t) sY (t)

(Y (t )) A(t)

A(t) — линейная модель Гудвина (в случае линейного акселератора).

TY (t) sY (t)

BY (t )

Линейная модель Гудвина асимптотически устойчива, если

B T

, s 0 .

16. Ранняя линейная динамическая модель Калецкого.
Берем основное макроэкономическое тождество Y C I A		, С Cа Сi сумма интенсивностей автономного
потребления вместе с индуцированным потреблением, Ci kY		индуцированное потребление, I Ia Ii
сумма интенсивностей автономных инвестиций вместе с индуцированными инвестициями, Ii sY
индуцированные инвестиции, 0 s 1, k s 1 . Решение об объеме инвестиций в момент времени t
определяется формулой	J (t) asY (t) bK(t) (t) , где 0 a 1, b 0 , (t) случайное отклонение,
	дискретное запаздывание по времени получения ОПФ. Средняя величина ввода
невязка. K (t) J (t )

инвестиций за промежуток времени

(t

,t)

:

		1	t
	I (t)
			t

J (s) ds

.

1

t

d

1

1

Преобразуем выражение I (t)

K (s ) ds =

t

(K (t )

ds

K (s ) |t

=

t

равенство Y C I A , причем

С Cа Сi

, Ci kY

, получим Y (t)

1

(I (t)

s

Y (t)

1

(K (t ) K (t))

1

( A(t)

Ca (t)) . Подставим это выражение и

J (t)

s

s

J (t) asY (t) bK(t) (t) :

1

(K (t ) K (t)) a( A(t) Ca (t))

K (t ) a

a

K (t ) (

a

b)K (t) a( A(t) Ca (t) (t)) .

Получили K (t )

Если t

преобразуется в t

, то уравнение примет вид:

K (t)

a

K (t) (

a

b)K (t ) a( A(t ) C (t ) (t )) .

a

	K (t)) . Далее используем
	A(t) Ca (t))			=
	d	K (t )	в формулу
	dt
	bK(t) (t)

Получаем ЛДРУ первого порядка стационарного типа (все коэффициенты и запаздывания равны const).

a x(t) b x(t )

f (t)

x (t)

Сравнивая уравнение:

1

1

,

x( ) ( ),

0,

t 0

1

находим

a

a1 , b

a

b1

,

f (t) a(A(t ) Ca (t ) (t )) .

Из условий задачи получаем: 0 a

1, значит

1

a1 0

,

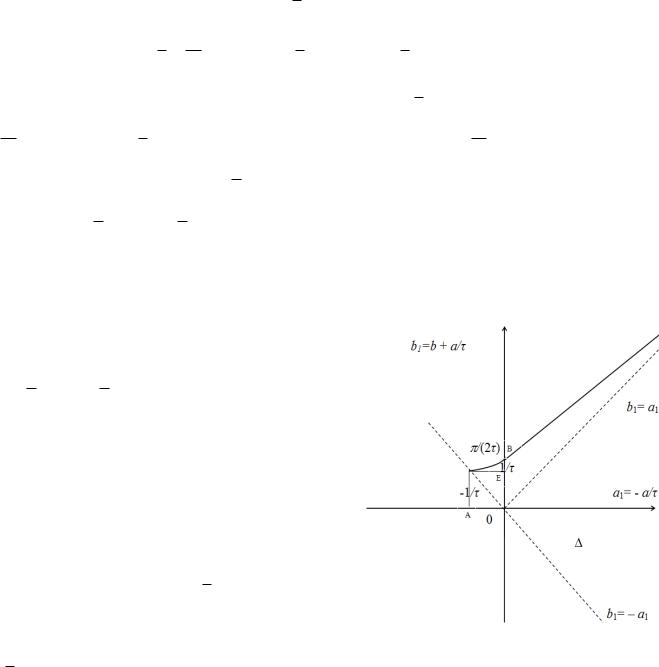
b1 0 . Асимптотическая устойчивость будет иметь место,

когда точка (a1,b1 ) (OAB) . Этот треугольник состоит из

равностороннего треугольника OAE и криволинейного

треугольника EAB. Попадание точки

(a1, b1 ) в равносторонний

треугольник OAE означает:

a1

b1 1 , или:

a

b

a

1

,

из которого следует, что 0 b

1 a

, откуда 0 a 1 b ,

0 b

1

.

Устойчивость модели Калецкого и зависит от значения коэффициентов а и b в уравнении реакции системы.

Коэффициент а выражает реакцию («чувствительность») инвестиционных решений на накопление (валовые сбережения), которые в некоторых условиях (когда накопляют только капиталисты) совпадают с непотребленной частью валовой прибыли капиталистов. Как видим, необходимым (но не достаточным) условием устойчивости является а < 1, объем инвестиционных решений должен быть меньше валового накопления.

Коэффициент b выражает реакцию («чувствительность») инвестиционных решений на запасы наличного основного капитала.

17.Поздняя линейная динамическая модель Калецкого.

Вданной модели предполагается, что капиталовложения производятся не только в основной капитал, но и в запасы сырья, готовых продуктов и незавершенное производство.

Пусть	Ik будет фактической величиной капиталовложений в основной капитал, Is капиталовложения в запасы,
так что I Ik Is . Затраты на запасы принимаются зависящими от изменений в выпуске продукции с
фиксированным временным отставанием
		Is (t) Js (t 1) B1Y (t 1) ,
где B1	инвестиционный коэффициент,	1 отставание. Предполагается также, что фактические затраты на

основной капитал производятся одновременно с установкой оборудования, то есть с оплатой поставок, но имеют

фиксированное запаздывание			2	, причем 0 1			2 , по отношению к соответствующим решениям об
инвестициям:	Ik (t) Jk (t						Jk (t) характеризует утвержденные решения об инвестициях в
			2 ) K (t) (*), где
основной капитал в момент t , а				K (t)		величина основного капитала.
В качестве факторов, влияющих на решения об объеме инвестиций								Jk (t) принимаются: норма сбережений,
изменения в скорости выпуска продукции (оба фактора влияют на увеличение Jk в прямом направлении) и
изменения в величине основного капитала (оказывает противоположное влияние на величину										Jk ). Тогда
										(**)
J (t) a S(t) B2Y (t) bK (t) (t)						,то есть J (t) as Y (t) B2Y (t) bK (t) (t) .
Из уравнений (*) и (**) получаем
Ik (t 2 ) Jk (t) as Y (t) B2Y (t) bK (t) (t) as Y (t) B2Y (t) bIk (t) (t) .
Далее сложим:	Ik (t								будет среднее запаздывание (взвешенное по
		2 ) b Ik (t) as Y (t) B2Y (t) (t) . Пусть
b ), такое, что	Ik (t 2 ) b Ik		(t)	Ik		(t ) ( 0 2 ), и примем			неизменным. Тогда предыдущее уравнение
	1	b
перепишется так: Ik (t )			1
					asY (t) B2Y (t) (t) .
		1 b

Далее предположим, что отставание в создании запасов равно среднему запаздыванию инвестиций в основной

капитал ( 1	). Тогда из уравнения для Is , находим						Is (t ) B1Y (t) и
I (t ) Ik	(t ) Is	(t )	as		B			(t)
				Y (t) B1	2					.
			1 b			Y (t)		1	b
					1 b

	Наконец, пользуясь уравнением Y	1	I Ca	A , мы можем в этом уравнении оставить члены, содержащие
		s

либо только капиталовложения I (t) , либо только ЧВП Y (t) . Калецкий выбирает первый вариант и получает:

I (t )

as

1

I (t) C

(t) A(t)

B

B

1

(t)

2

I (t) C

(t) A (t)

1 b

a

1

1 b

a

1 b

s

s

a

1

B2

a

1

B2

(t)

I (t)

B

I (t)

Ca (t) A(t)

B1

Ca

.

1 b

1

1 b

(t) A (t)

1

b

s

1 b

s

1 b

Введя удобную подстановку и упростив, получим ранее записанное:

- дифференциально-разностное уравнение опережающего типа.

I (t) a1I (t) b1 I (t ) f (t), t 0

Здесь:

a1

as

,

b1

(1 b)s

,

B1 (1

b) B2

B1

(1 b) B2

			s			1		(t) (t
f (t)				A(t) Ca	(t) (B1(1 b) B2 )
			b) B2				A (t) Ca
	B1	(1				s

По смыслу 0 a1 b1	и при достаточно малом			уравнение неустойчиво.
Выведем теперь уравнение для ЧВП: Y		1	I C		A , I sY Ca A,	I
				a
		s

Y (t) a1Y (t) b1Y (t ) f1(t), t 0 , где

)

.

sY C
a

A

, и наконец,

f1	(t)	1				Ca (t) A(t) b1	Ca (t ) A(t )		.
		s		f (t) Ca (t) A (t) a1

18. Односекторная динамическая нелинейная модель ВВП Рамсея-Солоу-Свена. Исследование модели Рамсея-Солоу-Свена.

	Обозначим X ВВП. Справедливо равенство	X I C , I – инвестиции, C – конечное потребление, k u					C
							X
	доля непроизводственного потребления, s 1 k 1 u				I	– доля произв. накопления.
					X
	Основное уравнение динамики ОПФ имеет вид K			I K		, норма амортизации. Здесь предполагают, что

–

L(t) = L e t , L(t) людские ресурсы,

x(t)

X (t)

– производительность труда, k(t)

K (t)

-

0

L(t)

L(t)

фондовооруженность (капиталовооруженность), откуда

K kL .

Продифференцируем последнее выражение:

K

I

K получим

(kL)

k L kL . Далее, из равенства K

k L kL I kL это уравнение динамики. При этом потребление I sX , X F(K, L,t)

–производственная

функция со степенью однородности один, явно зависящая от времени t.

Разделим обе части уравнения динамики на L:

k

k

L

s

X

K

, k sf (k,t) ( )k ,где

L

L

x

X

F (K, L,t)

1

F (K, L,t) F(

K

,

L

,t) F(

K

,1,t) F(k,1, t) f (k, t).

L

L

L

L

L

L

При 0 и u 1 s u(t) получаем модель Ф.Рамсея (F.Ramsey), 1928 г. При

0 и u 1 s const

получаем модель Р.Солоу (R.Solow) и Р.Свена (R.Swon), 1956 г.

k sf (k,t) ( )k,

Окончательно модель в удельных (относительных) показателях имеет вид

k(0)

k

.

0

Исследование модели Рамсея-Солоу-Свена (РСС)

Модель РСС в относительных показателях имеет вид

k

sf (k,t) ( )k .

Если заменить

k

на

k , то получим приближенное равенство

k s f (k,t) ( p)k прирост фондовооруженности.

Исследуем модель методами теории обыкновенных дифференциальных уравнений (ОДУ).

1) Проверка существования решения. Рассматриваемая модель

k

sf (k,t) ( )k нестационарное неавтономное нелинейное ОДУ первого порядка, для него необходимо

проверить существование решения.
Решение существует, если: f (t, k) непрерывна по t и k. В наших моделях предполагается непрерывность										f (t, k)
при t 0 и k 0 .
2) Решение единственно, если выполнено достаточное условие единственности решения:
а) существует		f	и непрерывна в рассматриваемой области;
	k
б) если выполнено условие Липшица: существует L 0 для любого				k	, k	2	из области |f (t, k ) f (t, k	2	) |
				1			1
L | k1 k2 | для любого t 0.

3) Существование стационарной траектории (решения), то есть такой траектории, что

k(t) const . При этом

траектория k(t) k* либо асимптотически устойчива (по Ляпунову), либо просто устойчивая (по Ляпунову), либо неустойчивая (по Ляпунову). Пусть k(t) k* . Подставим это выражение в уравнение, получим (k* ) 0 sf (k* ) – ( )k* , отсюда приходим к алгебраическому уравнению sf (k* ) ( )k* 0 .

Вданном случае при k0 > 0 все траектории асимптотически устойчивы. Это называется асимптотической устойчивостью (по Ляпунову) в целом (в данной области, то есть при k > 0).

Внаших примерах решение при k0 > 0 существует и единственно, то есть любой начальной точке соответствует

одна единственная траектория.

19.Задача оптимизации удельного потребления в модели Рамсея-Солоу-Свена. «Золотое правило накопления» Фелпса.

Модель РСС в относительных показателях имеет вид	k		sf (k,t) ( )k .

Существование стационарной траектории (решения), то есть такой траектории, что Уравнение для нахождения стационарной траектории:

k(t)

const

.

sf (k	*	) ( )k		*	0 .
Поставим задачу оптимизации, в том случае, когда							f (k)
имеет место строгая выпуклость вверх, причем
			:
sf (0) k
c c(k*) c(k *(s)) sup -задача оптимизации
	k* 0		0 s 1
Здесь		c(k*) (1 s) f (k*) f (k*) ( )k * в точке k*,
так как в этой точке sf (k*) ( )k *.
							это
Отсюда выписываем c (k*) f (k*) ( ) 0
необходимое условие экстремума. Здесь используется
правило дифференцирования сложной функции:
c (k *(s)) c (k*) (k*) 0 ,						(k* ) 0 – можно на этот
s					s	s
множитель сократить, получаем
c (k*) 0 необходимое условие экстремума.
«Золотое правило накопления» Фелпса
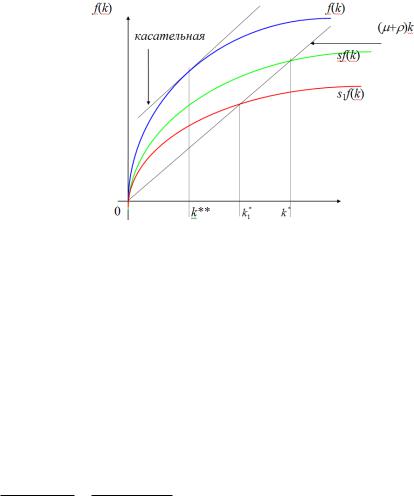
Геометрическая форма золотого правила имеет вид: в оптимальной стационарной точке								k ** касательная к
графику f (k)			параллельна секущей.Кроме того, если вычислить вторую производную							0
								c (k **) f	(k **)

есть точка максимума удельного потребления c(k**).

Действительно, в любой точке k* выполняется равенство sf (k*) ( )k * на стационарной траектории,
поэтому s	( )k *	.
	f (k*)
Затем в точке k* выполняется равенство						–	( ) 0	. – необх. условие экстремума.
			c (k **) f		(k **)
Найдем оптимальную норму накопления:			s **	( )k **			f (k **)k **		X	(K **, L **)	эластичность
				f (k **)			f (k **)		EK

, то

ВВП по капиталу (или по ОПФ).

Тогда s ** E X (K **, L K

РСС).

Рассмотрим пример. Для ПФ Кобба – Дугласа s ** FK , 1 s **

**) .Оптимальная норма накопления равна эластичности ВВП в точке k **( в рамках

имеем:

EL	1 .
F

20. Модель РСС с учетом научно-технического прогресса и с учетом запаздывания фондоообразования. Модель РСС с учетом научно-технического прогресса.

НТП – совокупность всех явлений и мероприятий, которые приводят к повышению выпуска продукции без повышения используемых ресурсов.

Автономный НТП – рост эффективности использования ресурсов не зависит от капитала и труда, а привносится извне и выражен в зависимости ПФ от времени.

Общий вид ПФ с учетом автономного научно-технического прогресса:		F(K, L,t) F0 (AK (t)K(t), AL (t)L(t))
F0 – ПФ степени однородности один (линейно однородная функция),		AK (t) – эффективность, темп роста
использования капитала, AL (t)	– эффективность, темп роста использования труда, KЭ (t) AK (t) K(t) –
эффективный капитал, LЭ (t)	AL (t) L(t) – эффективный труд.

Нейтральный НТП – автономный НТП называется Ф-нейтральным, если для некоторой функции Ф выполнено

Y

Y

, hLK

, LK ) 0

, Y – ЧВП, y

Y

– производительность труда, k

K

–

равенство Ф( y, k,YL ,YK , EL

, EK

L

L

фондовооруженность, Y

Y и Y

Y

– предельные производительности труда и капитала, EY

и EY

–

L

L

K

K

L

K

эластичности по труду и капиталу ,

hLK

K

– предельная норма замещения труда капиталом, LK

–

L

эластичность замещения труда капиталом.

1) Нейтральный НТП по Хиксу: рост экономической эффективности вследствие совершенствования техники, сопровождающийся неизменным распределением ЧВП между трудом и капиталом: h hLK (k) , то есть предельная норма замещения зависит от капиталовооруженности, в этом случае ПФ имеет следующий вид:

F(K, L,t) F0 (A(t)K, A(t)L) = A(t)F0 (K, L) , F0 (K, L) – линейно однородная ПФ, AK AL A – отдача капитала и труда одинакова. Нейтральный НТП по Хиксу означает равнодобавляющий, симметричный научно-

	технический прогресс, нейтральный по труду и капиталу:	F (K, L,t)	A(t) f0	(k) , A(t)	– темп роста
		L

производительности, f0 (k) – производительность без учета НТП.

2) Нейтральный НТП по Харроду: рост экономической эффективности вследствие совершенствования техники

при неизменности средней и предельной производительности капитала: YK		Y		Y	,
		K
				K

Y		Y		– средний продукт, то есть предельный продукт капитала зависит от среднего
K	– предельный продукт,
		K

продукта. ПФ в этом случае может быть записана в виде: F(K, L,t) F0 (K, AL (t)L) = F0 (K, LЭ (t)) . Нейтральный НТП по Харроду означает фондосберегающий (капиталосберегающий), трудоемкий, трудодобавляющий, трудорасходующий и, кроме того, удовлетворяет равенствам:

F (K, L,t)	F0	(k, AL	(t)) = AL	(t)F0		k
L						A	(t)
						L

Производительность эффективного труда:

	,1		A (t)
			L
	F (K, L,t)
		A (t) L
			L

f0
F
	0

k
A	(t)
L
(k	Э	(t

.

),1)

=

f	0	(k	Э	(t))

,

	k			K
		Э		L
				Э

	K
A	(t) L
L

.

3) Нейтральный НТП по Солоу: рост экономической эффективности вследствие совершенствования техники

при неизменности средней и предельной производительности труда:

Y		Y
L		L

Y
	L

,

предельный продукт труда зависит от среднего продукта труда. Нейтральный НТП по Солоу означает трудосберегающий, капиталоемкий, фондоемкий, капиталобавляющий, капиталорасходующий и, кроме

того,удовлетворяет равенствам:

F(K, L,t) F (A (t)K, L) = F (K

Э

(t), L) ,

0

K

0

F (K, L,t)

F (k

(t),1) = f

( A

(t)k) , k

KЭ

AK (t)K

.

L

0

Э

0

K

Э

L

L

Таким образом, в моделях РСС оптимальное удельное потребление может расти за счет научно-технического прогресса.