Razdatochnyy_material_2010

1.Производственные функции. Предельные и средние характеристики эластичности выпуска по

факторам.

Технол. закон – зависимость объема выпуска прод. от требующихся для этого затрат различных ресурсов. В мат. форме ТЗ=ПФ. ПФ устанавливает однозначную зависимость кол-ва выпускаемой прод.

от затрат всех ресурсов

y f (x) .

Требования к ПФ:

1.отражать св-ва реального производства

2.однозначно детермин.ированная функция

3.дважды непр. дифф. и однородна

4.ПФ-однородная функция cтепени однородности m>0, т.е f ( x) m f (x) , m-степень однородности;

m 1 объем производства растет; 0 m 1				снижение отдачи; m=1 эффект использования постоянен
	Аксиома	1:	при отсутствии хотя бы	одного	фактора	производство не возможно,	если
xi 0 i y f (x) 0
	Аксиома	2:	Увеличение значения фактора не		может	приводить к объема выпуска,	т.е.
dy	0,i 1, n	- эконом. область производств деятельности предприятия.
dx
i

Аксиома 3: Увеличение масштаба производства происходит с некоторой степенью однородности, yλ = f(λ x) = λ m f (x).

Аксиома 4: График поверхности произв. функции является выпуклым вверх: В случае двухфакторной ПФ аксиома строгой выпуклости вверх проверяется по следующим значениям миноров:

1			2		f
					2
1		x
				1

0

,

				2		f		2		f
1,2
	2		x			2	x			2
					1				2

		2	f		2
	x x
	1		2

0

.

Закон убывающей отдачи: если в производстве продукции используют малое количество ресурса, то на дополнительную единицу этого ресурса прирост выпуска продукции больше, чем в случае использования большего количества этого ресурса.

Экономические показатели на примере в случае двухфакторной ПФ:

1. Средний продукт (средняя отдача) ресурса вычисляется делением объема выпуска на величинуиспользования каждого ресурса. Средний продукт капитала λ K = y /K, средний продукт труда λ

L = y /L

2. Предельный продукт (предельная отдача) ресурса вычисляется по формуле частной производной производственной функции по фактору производства. Предельный продукт капитала µ K = y/ K, предельный продукт труда µ L = y/ L .

3. Предельная норма замещения трудозатрат капитальными издержками показывает прирост затрат на оплату капитала на один рубль прироста трудозатрат при неизменном объеме производства продукции. h = – dK/dL 0 при y = const. Величина h равна тангенсу острого угла наклона касательной к изокванте в точке определения, для которой вычисляется этот показатель

4. Эластичностью замещения ресурсов является своеобразный показатель, вычисляемый как эластичность показателя =K/L (фондовооруженность) по предельной норме замещения h. Его формула имеет вид = d /dh h / .

5. Показатель эластичности выпуска по фактору производства выражает предел отношения прироста выпуска к приросту использования соответствующего ресурса, эластичность выпуска по

y

y

E

капиталу

EK

= ( Y/ K)/(Y/K) или EK

= µK / λK

эластичность выпуска по труду

= µ L / λ L.

m

x2

m

x1

Примеры ПФ: 1.Леонтьева y min

;

2.Кобба-Дугласа

y ax

1

a

b

y	= ( Y/ L)/(Y/L) или
L

x2 .

	E	y
		L

y

ПФ

f (x

2. Предельная норма замещения факторов, эластичность замещения факторов.

устанавливает однозначную зависимость кол-ва выпускаемой прод. от затрат всех ресурсов

) .

На практике по разным причинам часто возникает необходимость замены одних факторов (ресурсов) другими. Предположим, что двухфакторное производство описывается производственной функцией у = f (К, L), где у - выпуск, К - капитал (основные фонды), L - трудовые ресурсы. Определенное

количество продукции можно произвести при различном сочетании используемых ресурсов. Зависимость
			капитала от труда при постоянном выпуске продукции ( y const ) можно
	K
			в общем виде выразить формулой K = ψ(L). Линия, соединяющая точки
			всевозможного сочетания используемых ресурсов (затрат на их оплату) при
			постоянном объеме производства продукции (дохода от ее реализации),
			получила название изокванты.
			Особенность изокванты состоит в том, что в любой ее точке уменьшение
			объема использования одного ресурса требует увеличения объема другого
		L	ресурса. График изокванты имеет форму, выпуклую к началу координат.
			При увеличении масштаба производства с пропорциональным ростом

затрат ресурсов изокванта смещается вправо вверх.

Изоклиналями называются линии наибольшего роста производственной функции. Изоклинали ортогональны линиям нулевого роста, т.е изоквантам. Уравнение изоклинали записывается в

форме:

	dK		dL
	( F K )		( F L)

В целях экономического анализа по изокванте K = ψ(L) при y = const можно вычислить три типа показателей: средние, предельные и эластичности.

Средний показатель, или соотношение используемых ресурсов, определяется, как отношение оплаты капитала к оплате трудозатрат =K/L. Средний показатель по форме совпадает с показателем фондовооруженности.

Предельная норма замещения трудозатрат капитальными издержками показывает прирост затрат на оплату капитала на один рубль прироста трудозатрат при неизменном объеме производства

	продукции. Он вычисляется по формуле h = –	dK		y / L	0 при y = const. Величина h равна тангенсу
		dL		y / K

острого угла наклона касательной к изокванте в точке определения, для которой вычисляется этот

показатель.

Например для ПФ Кобба-Дугласа: h = yL/yK = (а )/(а / ) = ( / ) ( ) = ( / ) .

Эластичностью замещения ресурсов является своеобразный показатель, вычисляемый как эластичность показателя по предельной норме замещения h. Его формула имеет вид = d /dh h / .

Например для ПФ Кобба-Дугласа: = d /dh h / = ( / ) ( / ) = 1.

3. Две динамические непрерывные модели развития предприятия.

Первая модель предприятия – модель Багриновского с зависимостью инвестиций от капитала и реализации без учета выбытия ОПФ.

В этой модели учитывается фонд развития предприятия, в который направляются средства, пропорциональные произведению величин производственного капитала и роста интенсивности выпуска продукции.

Обозначения:

I(t) – интенсивность капвложений в момент времени t,

u(t) – интенсивность отчислений от прибыли в фонд развития производства в момент времени t, k(t) – накопленное количество (объем, уровень) ОПФ в момент времени t,

y(t) – накопленное количество произведенной и реализованной продукции в момент времени t,y(t) k(t) – постоянная фондоотдача

Запишем функцию инвестиций:

u(t) a k(t)

y (t)

, где 0

a

1 - норматив отчислений,

Ind y(t)

y (t)

1

y(t)

1

y(t)

индекс роста (темп прироста) выпуска продукции.

Имеем

., то есть u(t)

a1

k(t)

k (t)

y(t) k(t) , при этом . k (t) I (t) u(t)

k(t)

a1 k (t) .

Запишем в классе изображений:

U ( p) a1( pK( p) k(0)) пусть k(0) k0

0 , тогда

U ( p) a pK ( p)

K ( p)

1

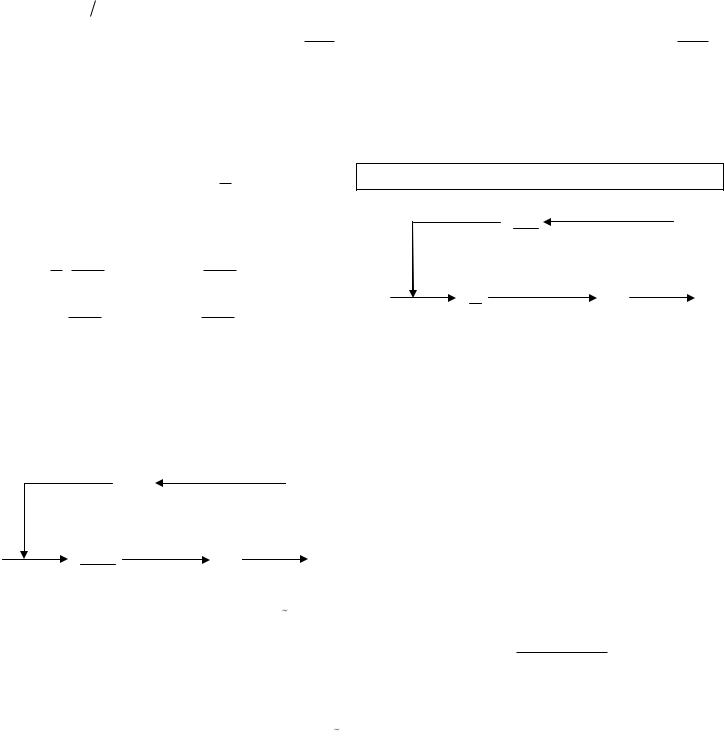
(I ( p) a pK ( p)) Структурная схема модели имеет следующий вид.

1

1

pK ( p) I ( p) U ( p)

p

u(t)

a

p

U ( p)

1

K ( p)

1

1

I ( p) k (t)

1

i(t)

p

1 a

1 a

i(t)

k(t)

y(t)

1

1

1

Y ( p)

1

I ( p) y (t)

i(t), y(0) 0

I ( p)

p

K ( p)

Y ( p)

a

1 a

p

1

1

1

–

Вторая модель предприятия Багриновского с зависимостью инвестиций от выпуска и реализации продукции с учетом выбытия ОПФ.

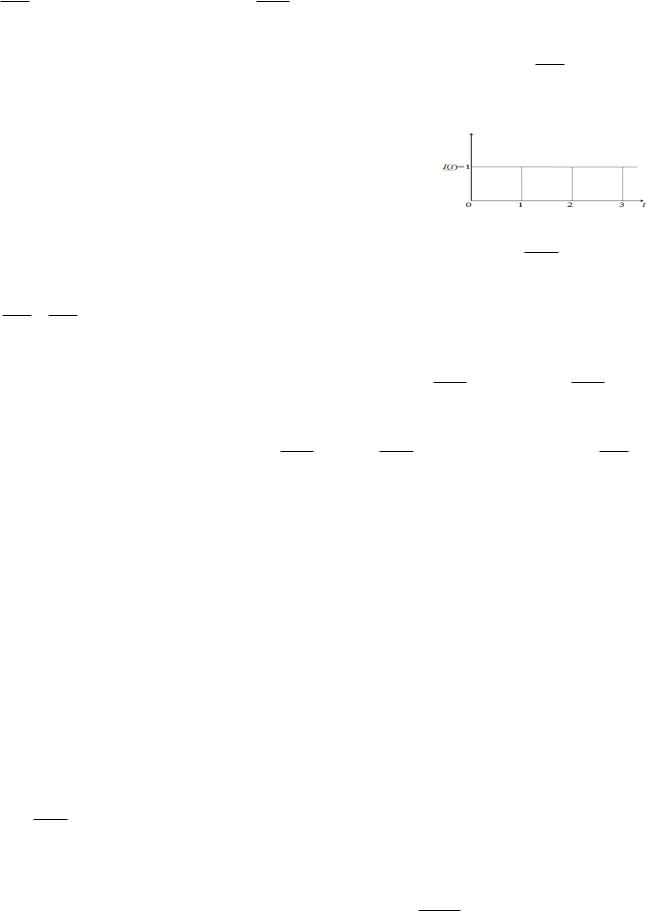
Структурная схема модели:

	u(t)
					a
	U ( p)
i(t)					k(t)			y(t)
			1
I ( p)		p	n		k( p)			Y ( p)
Для нахождения передаточной функции (

p)

В этой модели введено инерционное звено, отражающее запаздывание в процессе превращения инвестиций в ОПФ,

где n- норма выбытия.

модели воспользуемся основным ур-ем теории

автоматического регулирования с положительной обратной связью: Y ( p)

W ( p)

I ( p) ,

W ( p) ( p)

1

где W ( p) - передат. функция управляемого звена; ( p) - передат. Функция управляющего звена.

p n

В нашем случае W ( p)

и a , поэтому ( p)

, откуда Y

I ( p)

p n

1

a

p n a

p n a

p n

pY ( p) (n a )Y ( p) I ( p) .Модель в виде ЛОДУ:

y (t) (n a ) y(t) I (t) .

Т.к. y(t) k(t) , то модель виде ЛОДУ для ОПФ: k (t) (n a )k(t) i(t) .

4. Две динамические дискретные модели развития предприятия.

1. Первая модель предприятия. Без учета выбытия ОПФ.

Модель в виде ЛОДУ имеет следующий вид:

	1	I (t) для ОПФ F(t);			I (t)
F (t)	a		y (t)	a
1			1
				1

для выпуска продукции y(t), где

y(t)

F(t)

.

Дискретная модель получается следующим образом. Составим аппроксимацию

y (t) y(t) y(t 1) y(t) правая (нисходящая) разность, получим: y(t 1) y(t)

I (t)

(*)

1 a1

модель в виде ЛРУ.

Решим уравнение (*). Рассмотрим и решим однородное уравнение

y(t 1) y(t) 0

подстановкой y(t)

t

(метод Эйлера), получим

t 1

t

t

( 1) 0

, отсюда видим,

что

1

– характеристич. число.

Модель (уравнение) устойчиво, но не асимптотически.

Общее решение однородного уравнения: y(t) = y(0); t = y(0), то есть выпуск постоянный, отсюда

y(t) C1

t

C1 . Найдем частное решение неоднородного уравнения y(t 1) y(t)

I (t) при I(t) 1,

a

1

1

то есть когда интенсивность капвложений постоянная.

Видим

t

1

C частное решение неоднородного. ур-ия.

a

a

1 , откуда 1

1 , поэтому y*(t) = t

1

1

Общее решение неоднородного уравнения имеет вид: y(t) y(t) y *(t) C1

t

Ct C1 Ct

,

поэтому

y(t 1) C1 C(t 1) . Из уравнения видим y(t 1) y(t) C

1 , откуда

C

.

a

1 a

1

1

1

Далее y(0) C

0 C

, C y(0) .

1

1

1

Общее решение ЛРУ имеет вид:

y(t) y(0)

t

t y(0)

t ,

где

0 1,

0 a 1,

1

1

a

a

1

1

1

a

1

1

мультипликатор.

2. Вторая модель предприятия. С учетом выбытия ОПФ

Запишем непрерывную модель в виде ЛОДУ:
F (t) (n a )F(t) I (t) модель для ОПФ,		y (t) (n a ) y(t)
	y(t 1) (1 (n a ))
Положим y (t) y y(t 1) y(t) , отсюда

y(t)

I (t)

модель для выпуска продукции.

I (t), где 0 a 1, 0 n 1,

0 1 Решим однородное уравнение. Составим характеристическое уравнение (1 (n a )) 0 , откуда 1 (n a ) .

Равенство a = n означает = 1 (эквивалентность простой устойчивости решений однородного уравнения), т.е. в отсутствии внешних инвестиций выпуск постоянный: y(t) = y(0).

Общее решение однородного уравнения имеет вид:

y(t)

Найдем частное решение неоднородного уравнения при I получаем 1 , поэтому берем y* = C.

Общее решение неоднородного уравнения ищем в виде (*)

C		t	C (1 a n)	t
1	1		1

(t) = 1. Правая часть y(t) y(t) y *(t)

.

1 =

C
	t
1	1

1t,

C

= 1. В случае a n

,вычислим

y(t 1)

C		t 1	C
1	1

,

y(t 1) 1(1 a n) y(t)

C		t 1	C (1 a n)(C		C)
				t
1	1		1	1

C 1C ,

откуда	C		.Итак, получаем	y(t) C t					, откуда	y(0)
		1		1	1	1
		1						1

y(0) 0 . Вычислим

. Подставим это в (*):

1

n a

1

t

t

t

y(t)

y(0)

y(0)

1 y(0)

1

1 1

1

1

n a

n

1

n a

C1				,	C1	y(0)			, где
			1					1
	1					1

(1 t ) , где 1 a n .

a 1 1

5. Простейшие динамические паутинообразные модели и модель Гудвина рынка одного товара.

Рынок, на котором создается тенденция стабилизации цены на равновесном уровне (стремления к равновесной цене), является асимптотически устойчивым. Необходимыми условиями устойчивого движения рынка являются растущее предложение и убывающий спрос при увеличении цены. При этом крутизна падения спроса должна быть больше крутизны увеличения предложения, т.е. при условии что, D(P) = α – a P, S(P) = – β + b P, должно выполняться неравенство a > b.

По рис. движение цены можно объяснить следующим образом. Пусть в начальный момент времени цена равна P0. Это исходное состояние модели. Далее движение рынка можно описать по шагам.

Первый шаг. В начальном состоянии цена P0 низка и сложился дефицит

товара (предложение меньше спроса, т. е. S < D). При дефиците товара на

рынке возникает конкуренция покупателей, цена возрастает до уровня P1. На рынке создается новая ситуация.

Второй шаг. Продавцы увеличивают поставки товара, предложение при новой цене P1 высокое. Возникает избыток товара (предложение больше

спроса, т. е. S > D). При избытке товара обостряется конкуренция продавцов, цена падает до уровня P2. Ситуация на рынке опять изменяется. Теперь она аналогична положению, сложившемуся на рынке в начале первого шага.

Далее процесс продолжается так, как описано в первом шаге, цена снова возрастает до значения P3. Изменение цены продолжается до достижения точки равновесия. В данном случае рынок является

асимптотически устойчивым.

Модель Гудвина.

Продавцы ожидают, что сохранится цена предшествующего периода, но то и дело разочаровываются в такого рода ожиданиях. Поставщики ожидают, что если цена в течение одного периода находилась выше точки равновесия, то и в следующий период она будет в аналогичном положении. В действительности же в следующий период она может оказаться ниже точки равновесия. И модель исходит из предпосылки, что продавцы ничему не научились.

Цена в период t 1

равна Pt 1 . Пусть в период t цена, на которую рассчитывают поставщики, будет

Pt 1	Pt 2 , где Pt 2 – увеличение цена по сравнению с периодом t 2 , то есть Pt 2 Pt 1 Pt 2							,
а	– заданная постоянная. Величина означает вес (взвешивающий коэффициент), который продавцы
придают возможности поворота или сохранения направления движения цены. Если 0							, то какого-либо
изменения цены не ожидается; если 1 , ожидается полный поворот в движении цены.
Уравнение паутинообразный модели с линейными функциями имеем вид
	D(Pt ) S(Pt 1 )		= a Pt = b (Pt 1 Pt 2 )			,
Или, подставляя выражение P		, имеем:	a P b(1 )P		b P	.
	t 2		t	t 1	t 2
Отсюда находим: aPt b(1 )Pt 1		b Pt 2 .
Для ЛРУ второго порядка найдем условия асимптотической устойчивости:
		a b(1 ) b a b 0		,
		a b(1 ) b a b 2b 0			,
			a b 0 .

6. Динамические паутинообразные модели в случае нелинейных функций спроса и предложения.

Пусть нелинейная функция предложения

D D(Pt )

и

нелинейная

функция

спроса

S S(Pt 1 )

удовлетворяют

равновесию

D(Pt ) S(Pt 1 ) ,

где

S S(P) ,

D D(P)

–

непрерывно дифференцируемые функции для всех P > 0.

Разложим S(P) ,

D(P) в ряд Тейлора:

D(P) D(P*) D (P*)(P P*)

D (P*)

(P P*)

2

...

2!

S (P*)

(P P*)

2

... .,сравнив

S(P) S(P*) S (P*)(P P*)

2!

с линейной ДПМ ( D(P) aP(t),

S(P) bP(t) ),

видим, что D (P*) , S (P*) . Для линейной ДПМ

выполнено

b

1

- условие достаточной

a

S (P*)

D (P*)

P

D	S

P

Q*	Q

сходимости при P 0 . В общем случае сходимость – локальное свойство, т.е оно должно выполняться в окрестности точки равновесия.

Справедливы следующие достаточные условия локальной сходимости (асимптотическая устойчивость положения равновесия).

I. Точка для всех P 0

		)	– единственное положение равновесия и неравенство
(P	,Q
из некоторой окрестности этой точки P					.

S (P) D (P)

выполнено

II. Точка

)

– единственное положение равновесия и выполнено условие для эластичности:

(P

,Q

S

D

) .

EP

(P

) EP (P

Пример. Пусть функция спроса такова: S bP

m

, m 0 , b 0 , а функция предложения – D aP

n

, n 0

,

1

m

n

a m n

a 0 . Точку равновесия найдем из условия D = S:

bP

aP

, тогда получим P

b

m 1

n 1

a m n

a

m n

S

D

сходимости:

S (P

) bm

D (P

) an

или

EP

(P

) m EP

(P

) n .

b

b

. Условие

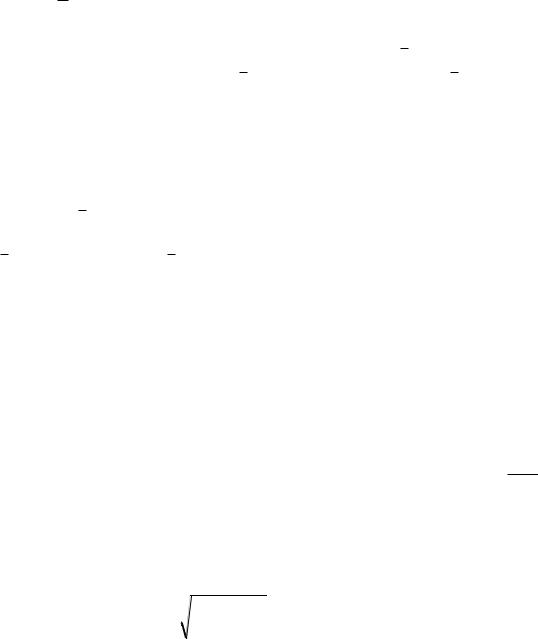
7.Динамические паутинообразные модели с учетом изменения запаса товара и с учетом зависимости скорости изменения цены товара от отклонения его текущего запаса от фиксированного запаса.

Для дискретного случая обозначим запасы в конце интервала t через Qt . Тогда
Qt Qt 1 Qt	Qt 1 St Dt представляет собой увеличение запасов на протяжении интервала t .
Ожидаемые St	и Dt , или планируемые предложение и спрос, равно как и фактические значение St

могут быть различными.

Модель 1. В период t торговцы устанавливают цену Pt согласно следующему условию: цена будет выше, если в предшествующий период запасы уменьшились, и ее повышение пропорционально сокращению запасов. Имеем Pt Pt 1 Qt 2 , где – заданная положительная величина. Далее

Dt aPt	, St bPt и	Qt 1 Qt 2 Qt 1 Qt 2 St 1 Dt 1 ( ) (a b)Pt 1 .
Уравнение	Pt Pt 1 Qt 2	сводится к следующему: Pt	Pt 1 ( ) (a b)Pt 1	,
то есть Pt [1 (a b)]Pt 1 ( ) .
Полученное ЛРУ первого порядка будет асимптотически устойчивым, если корень					его
характеристич. уравнения [1 (a b)] 0 будет |			| 1. Решаем неравенство |1 (a b) | 1			,

и Dt

,

получаем 0 a b	2	.
Модель 2. Торговцы устанавливают цену			Pt	в период t следующим образом: цена повышается, если в
предшествующий период уровень запасов упал ниже данного объема Q , и это повышение цен

пропорционально нехватке запасов до объема Q . Таким образом	Pt	Pt 1 (Q Qt 1 ) ,
где – заданная положительная величина.

Как и раньше, Dt aPt , St bPt .

Для определения величины запасов Qt произведем суммирование назад вплоть до начального момента

(

t

0

):

		t 1
Q	Q		Q
t 1	0		k
		k 1

0		t 2	k
Q			Q
		k 0

0		t 1		t
			S
Q
		k 1

D
t

Q0

t1

[ (

k 1

) (a

b)Pt

]

.

Уравнение Pt			Pt 1 (Q Qt 1 )			тогда позволит определить цены на все периоды вплоть до начального.
Но эту зависимость от движения цен в предшествующие периоды можно выразить и иначе:
Pt	Pt 1 (Q Qt 1 ) и Pt 1 Pt 2 (Q Qt 2 ) .
Произведем вычитание: Pt Pt 1						Pt 1 Pt 2 (Qt 2	Qt 1 ) .
Преобразовывая полученное уравнение, можно затем переписать уравнение следующим образом:
P 2P		P	(S	D	) , то есть P [2 (a b)]P			P	2	( ) .
t	t 1	t 2	t 1	t 1		t	t 1	t

Для ЛРУ второго порядка найдем условия асимптотической устойчивости:

a		a a		0	1 [2 (a b)] 1 (a b) 0
	0	1	2
		a1 a2		0		[2 (a b)] 1 4 (a b) 0
a0					1		,
		a	a			1 0
					1
		0	2

Видно что, условия асимптотической устойчивости не выполнено. Проведем доп.исследования:

k	2	(2	(a b))k 1 0	- характ. ур-ие. Осуществим камфорное преобразование: k	w 1
					w 1

b0 w2 b1w b2 0

	b0	a0 a1 a2
	b1 2(a0 a2 )
	b2	a0 a1 a2
	(a b)w2 (4 (a b)) 0 w		(a b) 4 , a b 0, 0
		1,2	(a b)
	при (a b) 4 >0 будут чисто мнимые корни, значит при 0 a b				4	модель устойчива.

8. Динамические непрерывные модели Вальраса-Эванса-Самуэльсона рынка одного товара: простейшая модель, модель с учетом инерции цены продавца.

Особенность моделей Вальраса состоит в том, что рынок рассматривается автономно, без влияния экзогенных процессов. Предполагается, что переменные P, D и S – непрерывные функции времени t. Линии спроса и предложения заданы следующими формулами: D(P) = – aP, S(P) = – + bP

Скорость роста цены пропорциональна дефициту товара на рынке с постоянным коэффициентом пропорциональности .

Модель имеет вид ЛОДУ dP/dt = (D – S), где dP/dt – скорость изменения цены, разность D – S составляет дефицит товара, – коэффициент скорости реакции покупателей на дефицит товара.

Для решения уравнения dP/dt = (D – S) подставим в него формулы D(P) и S(P) и получим иную запись дифференциального уравнения: dP(t)/dt = ( + ) – (a + b)P(t).

В точке равновесия скорость изменения цены равна нулю, поэтому дифференциальное уравнение приобретет

следующий вид: 0 = ( + ) – (a + b)P*, где P* – равновесная цена.

Из уравнений dP(t)/dt = ( + ) – (a + b)P(t) и 0 = ( + ) – (a + b)P* составим систему dP(t)/dt = ( + ) – (a + b)P(t),

0 = ( + ) – (a + b) P* .

Вычтем из первого уравнения системы второе, получим dP(t)/dt = – (a + b)(P(t) – P*) .

Для решения этого уравнения введем обозначение R(t) = P(t) – P*, тогда dR(t)/dt = dP(t)/dt, где

R(t) - отклонением цены от равновесного значения P* = ( + )/(a + b), превышением цены P(t) над равновесным значением P* в случае дефицита или занижением цены в случае избытка товаров. Подставив R(t) и dR(t)/dt в

дифференциальное уравнение dP(t)/dt = – (a + b)(P(t) – P*), получим dR(t)/dt = – (a + b)R. Уравнение имеет решение R(t) = R0 e - (a + b) t.

Таким образом, отклонение от равновесной цены изменяется по экспоненциальному закону.

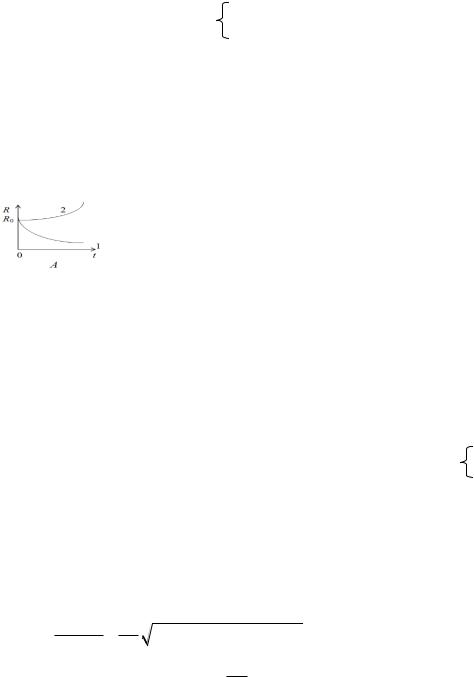
В зависимости от знака показателя степени процесс R(t) будет либо монотонно приближаться к равновесной цене (отриц знак – кривая1), либо монотонно удаляться в бесконечность (кривая 2).

Эти два графика отражают динамику двух качественно разных рынков: первый –

асимптотически устойчивого рынка, второй – неустойчивого рынка. В этой модели не возникают колебания цены, в частности, не возникают циклы.

Модель с учетом инерции цены продавца. Теперь рассматривается модель конкурентного рынка, в котором продавцы реагируют на изменение цены равновесия не мгновенно, а с некоторым запаздыванием. Запаздывание будем моделировать с помощью введения в систему инерционного звена первого порядка: P(t) – входной процесс звена, y(t) – реакция звена. Модель звена имеет вид T y'(t) + y(t) = P(t),

где T – временной лаг (среднее запаздывание). Предложение S с учетом ценовой динамики имеет следующий вид: S(y(t)) = – β + b y(t), где β, b – постоянные коэффициенты.

Динамика спроса D без дополнения, введенного в предыдущем пункте, описывается равенством D(P(t)) = α – a P(t), где α, а – постоянные коэффициенты.

Скорость изменения цены спроса на рынке пропорциональна рассогласованию между спросом и предложением товара с коэффициентом пропорциональности λ > 0: P'(t) = λ D(P(t)) – S(y(t)) .

Таким образом, моделируемый объект описывается системой уравнений P'(t) = λ (D(P(t)) – S(y(t)) ,

T y'(t) + y(t) = P(t)

При нулевых начальных условиях P0 = 0 и y0 = 0 система уравнений в форме изображений примет следующий вид: p P(p) = λ α /p – а P(p) + β/p – bY(p) , Tp Y(p) + Y(p) = P(p).

Подставим выражение P(p) из второго уравнения в первое и после преобразования получим

Tp2 Y(p) + (1 + λ аT)p Y(p) + λ(а + b)Y(p) = λ(α + β)/p.

Выражению соответствует модель цены предложения в форме ЛОДУ второго порядка:

T y'' (t) + (1 + λаT) y'(t) + λ(а + b) y(t) = λ(α + β). По виду процесса y(t) определим, является ли рынок устойчивой системой. Характеристическое уравнение системы имеет вид T p2 + (1 + λаT)p + λ(а + b) = 0.

Анализ движения цены предложения будем проводить на основании корней характеристич. уравнения

		1 aT		1	(1	aT )	2	4
1,2		2T		2T

определяется неравенствами: a 1

T

(

,

a b)T . Таким образом, область асимптотической устойчивости

a b 0 .

9. Динамические непрерывные модели ВЭС рынка одного товара: модель с учетом зависимости спроса и

предложения от скорости изменения цены, модель с учетом дискретного запаздывания цены продавца.

В формулу спроса и предположения дополнительно введем слагаемое учета скорости изменения цены. Скорость изменения цены выражается производной P'(t). Формулу предложения и спроса запишем в динамическом виде

равенством S(P(t)) = – β + bP(t) + k1 P'(t), D(P(t)) = α – aP(t) – k2 P'(t),

где α, а, k2 β, b, k1 > 0 – постоянные коэффициенты.

Скорость роста цены пропорциональна дефициту товара на рынке. Поэтому модель рынка записывается в виде уравнения P'(t) = λ D(P(t)) – S(P(t)), где λ – коэффициент пропорциональности, имеющий положительное значение. Подставив в P'(t) = λ D(P(t)) – S(P(t)) выражения для D(P(t)) и S(P(t)), запишем дифференциальное

уравнение рыночной системы в виде P'(t)= λ α – a P(t) – k2 P'(t) + β – bP(t) – k1 P'(t)

или, k = k1 + k2, в виде (1 + λk) P'(t)= λ(α + β) – λ(a + b)P(t).

Постоянные коэффициенты для упрощения записи формул будем обозначать:

А = λ(α + β)/(1 + k λ), В = λ(а + b)/(1 + k λ), k = k1 + k2. Теперь дифференциальное уравнение можно переписать в следующем виде: P'(t) + B P(t) = A. Выведенное дифференциальное уравнение решим с помощью операционного

исчисления: P'(t) + BP(t) = A ↔ pP(p) – P0 + ВP(p) =А/p.

Решим полученное уравнение относительно P(p): (p + B) P(p) = А/p + P0, P(p) = А/[p (p + B)] + P0/(p + B). Разложим это изображение на простейшие слагаемые: P(p) = (А/B) [1/p – 1/(p + B)] + P0/(p + B),

P (p) = (P0 – А/B) 1/(p + B) – (А/B) 1/p.Оригинал этого изображения: P(t) = (P0 – А/B) exp (– Bt) – А/В является решением данной задачи

Таким образом, цена изменяется по экспоненциальному закону. При больших значениях t темп изменения цены
можно считать равным B = – λ(а + b)/(1 + k λ), где а, b, k > 0 и λ > 0 – постоянные коэффициенты.
Выводы рассматриваемой рыночной системы совершенной конкуренции:
1.	Рыночная цена изменяется по экспоненциальному закону. Характер изм.цены на рынке монотонный.
2.	Устойчивость зависит только от значений постоянных параметров модели а, b, k > 0 и λ > 0.	В

стандартом случае, то есть, когда а > 0, b > 0, будет B > 0, поэтому система с учетом скорости изменения цены всегда асимптотически устойчива. Цена P(t) будет монотонно приближаться к равновесному значению. В случае произвольных параметров α, β, а и b при k > 0 и λ > 0 рыночная система будет асимптотически устойчивой тогда и только тогда, когда а + b > 0.

модель Вальраса-Эванса-Самуэльсона с учетом дискретного запаздывания цены продавца

Теперь рассматривается модель конкурентного рынка, в котором продавцы реагируют на изменение цены равновесия не мгновенно, а с некоторым дискретным запаздыванием.

Предложение задано формулой D(P) = – aP, где , а – постоянные коэффициенты, предложение S с учетом ценовой динамики имеет следующий вид: S(P(t – τ)) = – β + b P(t – τ),

где β, b – постоянные коэффициенты. Скорость изменения цены спроса на рынке пропорциональна рассогласованию между спросом и предложением товара с коэффициентом пропорциональности λ > 0: P'(t) = λ D(P(t)) – S(P(t – τ)). Подставим выражения для D(P(t)) и для S(P(t – τ)), получим

P'(t) + λ a P(t) +λ b P(t – τ) = λ (a + b).

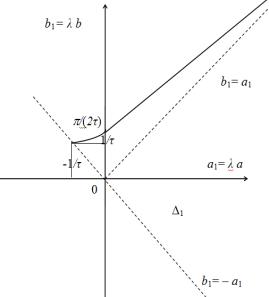
Будем рассматривать это уравнение при t ≥ 0, зададим P(ξ) = P0(ξ) при ξ < 0. Если обозначим a1 = λ a, b1 = λ b, f(t) = λ (a + b), тогда возникает ЛДРУ первого порядка

P'(t) + a1 P(t) + b1 P(t – τ) = f(t), P(ξ) = P0(ξ) при ξ < 0.

Уравнение асимптотически устойчиво эквивалентно тому, что точка с координатами (a1, b1) 1. При этом граница b1= – a1 до точки a1 =

– 1/τ (не включая эту точку) означает простую устойчивость. Точка

(0, /(2τ)) означает также простую устойчивость.

10. Динамическая непрерывная модель ВЭС рынка одного товара с учетом зависимости скорости изменения цены товара от отклонения его текущего запаса от фиксированного запаса.

	В случае непрерывного анализа запасы, подобно другим переменным D ,	S и	P , непрерывно
	изменяются во времени. По определению, если запасы в момент t составляют	Q(t)	, то	dQ	S D
				dt

	t
и Q Q0		(S D) ds .
	0

скорость возрастания

Q :

В каждый момент времени торговцы устанавливают цену P так, что цены пропорциональна разности запасов по сравнению с заданным уровнем

dP dt

(Q Q) [Q0

tQ (S

0

D)

ds]

, где

— заданная положительная величина. Имеем

	d	2	P			dQ
							(S D) , и ускорение возрастания цен пропорционально скорости уменьшения
	dt		2			dt
	запасов. При линейности функций и отсутствии запаздываний
	d	2	P
				(S D) (a b)P ( ) . Характеристическое уравнение модели имеет вид
	dt		2
			(a b) 0 .
		2
	Если a b 0 , то 1,2 i (a b) , и уравнение просто устойчиво. При a b 0							, получаем
	1,2				(a b) , то есть уравнение неустойчиво. Невероятный случай a b 0			приводить к

неустойчивому уравнению.

модель Алена

Модель именно так, чтобы в каждый момент времени t цена P устанавливается так, чтобы спрос полностью поглощал предложение, с одной стороны, и чтобы предложение полностью поглощал спрос, с другой, то есть

функции D(t) и S(t) удовлетворяли уравнению:

Если функции линейны, то S(t) bP(t)

	и мы получаем	dP(t)		a b	P(t)		,где
		dt		k		k

D P,

k1P (t k k1

dP
dt
) , k1
k	2

 

S 0 0

 

,

.

P,	dP
	.
	dt
D(t)

Модель рынка асимптотически устойчива тогда и только тогда, когда

aP(t) k	P (t)
2

a b 0 .

,

k	2

0

,

Модель Маршалла Если в какой-либо момент времени объем предложения отличается от уровня его, обеспечивающего равновесие, то

ожидаемые цены, которые покупатель готов заплатить, будут отличны от цен, приемлемых для продавца. Построим динамическую модель, в которой объем предложения увеличивается, если цены продавцов ниже тех, которые предлагают покупатели. Пусть скорость этого увеличения пропорциональна размерам дефицита.

Получаем: цена покупателя – P Q , цена продавца –

P Q

D

a

S

b

dQ

(PS PD ) ,

dQ(t)

(

Q(t)

Q(t)

dQ(t)

1

1

b a

и

)

Q(t)

,

dt

dt

b

a

dt

ab

a

b

где

по-прежнему означает скорость реакции.

Характеристическое уравнение модели имеет вид (

1

1

) 0 .

a

b

Асимптотическая устойчивость будет иметь место тогда и только тогда, тогда 1a b1 0 , это будет возможно, если a b 0 , ab 0 или, если a b 0 , ab 0 .