Razdatochnyy_material_2010

Модель РСС с учетом запаздывания фондоообразования Итак, баланс ВВП в абсолютных показателях имеет вид удельных показателях.

Здесь ВВП X F(K, L) , удельный ВВП имеет вид: x

X I C

F (K, L) L

, что эквивалентно

	= F (	K	,	L	) F (	K
		L		L		L

x i ,1)

f

c баланс в

(k) по свойству

однородности первой степени.

Далее, I sX

соответственно i sx

,

C (1 s)X , соответственно

c (1 s)x .

Динамика ОПФ:

dK

V K , где V интенсивность ввода ОПФ в момент времени t. Таким образом,

dt

dK

V K

звено запаздывания ввода ОПФ, то есть инерционное звено, T

1

лаг, постоянная времени или

dt

n

запаздывания инерционного звена.

Уравнение

dV

nV nI описывает инерционное звено запаздывания ввода реальных инвестиций, где I

dt

запланированные инвестиции. Модель можно записать в виде TV V I домножим на обратную величину

T

1

.

n

Будем использовать обозначения

k

K

фондовооруженность, i

I

удельные инвестиции (накопления) на

L

L

одного человека,

c

C

удельное потребление, f

F

средняя производительность труда, v

V

.

L

L

L

Напомним, что

x i c , где f (k)

средняя производительность труда, i sx , c (1 s)x .

Из равенства K kL получим K

K

k L kL , откуда

k L kL V kL . Разделим последнее равенство на

L, получим k

k

L

v k .

L

		L		L e		t	, k v k k , k v ( )k .
	Учтем, что			0
		L		L e	t
				0

В уравнении			dV	nV nI подставим V vL . Вычислим V							ni (
			dt					v L vL		, откуда v
Получим систему двух уравнений первого порядка, запишем сразу задачу Коши
	k v ( )k,
v nsf (k) (n )v,
	k(0) k	,	v(0) v .
	0				0
Поставим задачу оптимизации (максимизации) удельного (подушевого) потребления.
					c(k*) c(k *(s)) max,
Следующая задача:						k* 0, или 0 s 1.

n)v

.

В точке k*:

I I (t) sf

X X (t) f (k*)L e t = Y (0)e t , K K(t) K(0)e t		,
	0
(k*)L e t = I (0)e t ,	C (1 s) f (k*) L e t = C(0)e t .
0	0

V

V (t)

V (0)e	t

,

				L(t )
Все переменные растут по экспоненциальному закону с индексом роста .
Вычислим c	C	(1 s) f (k*) f (k*) sf (k*) = f (k*)			(n )( )	k *.
	L				n
Заметим, что s*			(n )( )k *	.
			nf (k*)

Запишем производную с(k), найдем s** оптимальную норму потребления:

c (k **) f (k **) (n )( ) 1 0 . n

21. Двухсекторная динамическая нелинейная модель.

Выделяются два сектора экономики: I сектор: производство средств производства, II – производство предметов

потребления. Даны ПФ: X1 F1 (K1	, L) , X2 F2 (K2 , L2 ) , F1 ПФ производства средств производства, F2 ПФ
производства средств потребления.	L = L1 + L2 = const , L –общий объем трудовых ресурсов. Далее обозначим K1

ОПФ в первом секторе, K2 ОПФ во втором секторе. Инвестиции в первом сектор равны I1 = sX1, где s норма накопления. Аналогично: I2 = (1 s)X1 .Конечное потребление определяется равенством C = X2 = F2(K2, L2), причем

в первый сектор sF2																		, во второй сектор								(1 s)F2			, где 0 s 1. Распределение трудовых ресурсов постоянно: L1 =
qL, L2 = (1 q)L, где																		q доля трудовых ресурсов, занятых в первом секторе (0 q 1).
Запишем систему ОДУ:
K					s F (K										, L ) K				,
		1						1					1		1			1
	K				(1 s) F (K , L ) K																	,
																					2
			2												1		1	1
	C		F (K									, L ),
										2
						2							2
	L			qL,				L					(1 q)L,
		1										2
0 s 1, 0 q 1.
Здесь норма амортизации, 0 < 1, мы будем рассматривать случай s, q = const. Обозначим
k					K1		,	k						K2			,	f (k) F (k ,1) ,						f		(k) F (k					,1) .
									2																2
1					L1										L2			1	1			1						2		2
Тогда система примет вид:
k			sf (k ) k														,
	1					1		1							1
							q
k										(1 s) f (k ) k										,
	2					1 q											1	1	2
	C					F (K							, L )
											2					(1 q) F (k							,1) (1 q) f
						2									2													(k		),
L																											2		2
						1				L									2			2
							1 q						2
s const,													q const,
		s 1, 0 q 1.
0

Будем искать стационарные траектории, состояния равновесия, положения равновесия, то есть

k2 (t) k2

const , получим систему

k (t) k
1	1

const

,

0 sf (k ) k						,
			1	1	1
	0		q	(1	s) f		(k ) k		.
			1 q			1	1	2

Если каким либо образом нашли стационарную траекторию k1 , то отсюда находим k2

1

q

(1

s) f1 (k1*) ,

1

q

поэтому

c* (1 q) f2

(k2 ) . Задача оптимизации: среди всех стационарных траекторий найти такую, которая дает

максимум потребления с*.

Оптимальные для стац. траектории S **и

q **

находятся по формулам:

S ** E

x2

k **

q ** E x2

k

2

** f ' (k

2

**)

1

;

2

;

k11

f (k **)

k 2

f

(k

**)

2

2

1

1

x

S **X1

1

K1;

- инвестиции в 1 сектор = доход от капитала в 1-м секторе

K

1

(1 S **) X1

x

1

L1;

- инвестиции в 2 сектор = доход от труда в 1-м секторе

L

1

q **X

x2

K

;

- потребление раб. в 1сектор = доход от капитала во 2-м секторе

2

K2

2

(1 q **) X

x2

L ; - потребление раб. в 2сектор = доход от труда во 2-м секторе

2

L2

2

22. Статические модели Леонтьева: продуктивность матрицы прямых материальных затрат, достаточные признаки продуктивности, матрица полных материальных затрат, двойственная система модели Леонтьева система уравнений открытой модели Леонтьева.

Рассмотрим n отраслей, причем каждая отрасль выпускает только один продукт. Обозначим:

y col y1,

вектор чистого, конечного продукта (КП),

x col{x1,

, xn}

– вектор валового продукта (ВП),

A aij

матрица прямых материальных затрат (МПМЗ). Здесь aij – объем затрат (стоимостных или натуральных)

, y
n
–

i-го

–

продукта, необходимый для производства единицы j-го продукта: aij

количество i-го продукта, необходимого для производства xj единиц

xi

( xi1 xi 2

xin ) yi

, в матричной записи получаем: y = x –

	x
	ij		, где xj	– количество j-го продукта, xij –
	x
		j

j-го продукта. Отсюда

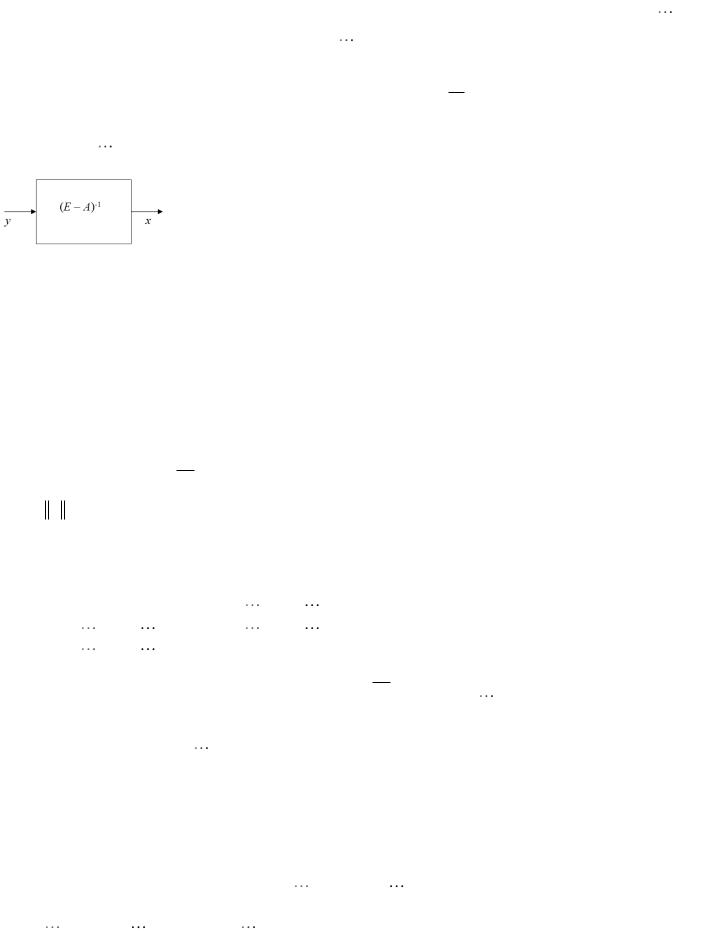
Ax - открытая статическая модель

a	x	a	x		a	x
i1	1	i 2		2	in	n

	Леонтьева. Здесь считается, что y –										вход (экзогенная переменная), x – выход
	(эндогенная переменная), А –								n n-матрица. Из теории матриц известно, что
	y R	n	! x R		n			(E	A)	1	. Кроме того, из экономического смысла следует:
	x 0,	y 0,		A 0. Это означает, что в пространстве n-мерных векторов и квадратных
n n-матриц введена частичная упорядоченность (полуупорядоченность): x 0 xi 0 ,
y 0 yi 0,	A 0 aij 0 .
В данной модели при А 0 возникает задача: y 0 !									x 0 (E A) 1 0 , то есть возникает задача об

условиях положительной обратимости матрицы Е – А.
Определение. Пусть A 0. Будем говорить, что A – продуктивная матрица, если y 0,				x 0 :	x Ax
Отсюда следует, что x 0 . Действительно, x y Ax 0, т.к y 0, Ax 0 .
Достаточные признаки продуктивности неотрицательной матрицы:
1. (A) 1 (E A)	1	0	A – продуктивная матрица.
Здесь ( A) max{| k |}		– спектральный радиус матрицы А, k при k=1,…,n, – собственные числа матрицы
k 1,n
учетом кратности, k	: k 1, n ( A) Sp( A) – спектр матрицы А.

y

А

.

с

2.Если A 1,		A 0 ( A) 1		(E A)	1	0 A – продуктивная матрица.
Матрицы полных материальных затрат.
Пусть A 0, (A) 1 A – продуктивная матрица (E A)							1	0 . Тогда система x Ax y однозначно
разрешима: x (E A) 1 y , (E A) 1 B – матрица полных затрат (МПЗ), матричный мультипликатор
Леонтьева. При этом x			2	n		) y, где А – матрица прямых материальных затрат (МПМЗ),
			(E A A	A
E A A2		An	- МПЗ, A2	An - матрица косвенных затрат (МКЗ). Заметим, что
2		n	- ряд Неймана для матрицы А. Таким образом, МПЗ = E + МПМЗ + МКЗ.
E A A		A

Двойственная система модели Леонтьева

Система состоит из уравнений вида

			n
p	j		a p v			,
			ij	i	j
			i 1

j

1, n

, где

p ( p1,

, pn )

– вектор цен продуктов

(ресурсов, товаров), pj – цена единица j-го продукта, vj – прибыль (добавленная стоимость) от производства

единицы j-го продукта, v (v1,	, vn ) .Систему можно записать в матричном виде p(E – A) = v. При этом говорят,
что А – прибыльная матрица А – продуктивная матрица. То есть, v 0, p 0 : p(E A) v
( p 0) . Все свойства прибыльности изучаются аналогично свойствам продуктивности.
Система уравнений открытой статистической модели Леонтьева
Система состоит из двух систем: (E A)x y и		p(E A) v . Первая описывает производство, вторая –
прибыльность производства.
Пусть L – общие затраты труда,	L = lx, где l = (l1,…,ln)		– вектор трудоемкостей, x = (x1,…xn) – вектор валовых
продуктов, валовых выпусков. Тогда L l1x1		ln xn	L1	Ln .

Пусть, далее, w – ставка заработной платы, номинальная заработная плата, цена единицы трудовых ресурсов,

v {v1, , vn} {l1w, ,ln w}, v1 l1w, , vn ln w . Тогда v = lw. В этой ситуации заданы y и v. Требуется найти x, p, L1,…,Ln, L.

23. Разложимость матрицы прямых материальных затрат, независимые и фондообразующие отрасли, предельный анализ модели Леонтьева, замкнутая статическая модель Вальраса-Леонтьева.

Определение. А – разложимая матрица существуют одновременные перестановки строк и столбцов с

одинаковыми номерами такие, что матрица принимает вид:

A
A	1
	0

	A
	2
	A
	3

Определение. А – неразложимая матрица с помощью одновременной перестановки строк и столбцов с одинаковыми номерами матрицу нельзя привести к треугольному виду i, j существует набор индексов

i1,i2 ,	,im , где i = i1, j = im такой, что любой элемент последовательности 0, то есть ai i				0	. Матрицу, не
				k k 1
являющуюся неразложимой, назовем разложимой.
В случае неразложимости матрицы A возникает последовательность ai i		0, ai i	0,	,	ai	i	0 – «дорожка
	1 2	2 3			m 1 m

невырожденности». В случае модели Леонтьева неразложимость матрицы означает, что любая отрасль косвенно использует продукцию любой другой отрасли. В этом случае нельзя разделить отрасли на изолированные группы. Независимые и фондообразующие отрасли.

Пусть A 0 , A – разложимая матрица, то есть ее можно представить в следующем

виде:

		m	n m
A ~ A		A	A
		1	2
		0	A
			3



m n m

.

Здесь продукция отраслей с номерами m +1, …, n не используется в отраслях с номерами 1, …, m. Статистическую

модель Леонтьева (E - A)x = y

в этом случае можно записать так:

	A
E		1
		0

A		x
			1
2					Y
A
3		x
			n

, где

x	a	x a		x	a	x
m 1	m 1,1	1	m 1,2	2	m 1,m 1	m 1
	0		0		0

ym 1

, то есть последние n – m отрасли не нужны для первых m

отраслей, первые m отраслей – фондообразующие. Теорема (Перрона–Фробениуса).

		ˆ
1) Если A 0 (A) s(A) A 0 – собственное число матрицы А (число Фробениуса матрицы А)
xA 0 : AxA A xA , то есть xA – собственный вектор матрицы А (вектор Фробениуса матрицы А).
		ˆ
2) Если А 0, А – неразложима (A) s(A) A 0 xA 0 .
Предельный анализ модели Леонтьева.
Пусть (E A)	1	0 , то есть A - продуктивная матрица. Тогда x = B y	и p = vB, v = lw p = lwB, L = lx = lBy.
Сформулируем задачи предельного анализа.
1. Изменение валового продукта в зависимости от конечного продукта: xi				y j xi y j bij .

2. Изменение затрат труда в зависимости от выпуска конечного продукта: L

y j

L

L

n

L

n

L

L

т.к. L L1 ... Li

... Ln

, L l x ,

i

libij

,

i

i

i i i

y j

y j

y j

y j

y j

i 1

i 1

	L	n	Li		Li
		libij ,				libij ,
	y j		y j		y j
		i 1

libij

В частности,

n

p j w libij

i 1

y	j			1	,	y	j	1
L			l b			L
	i		i	ij

w L , откуда

y j

	n
	libij . Для двойственной задачи имеем: p v(E A)									1	vB lwB ,
	i 1
	w			y j	, где	w	- реальная з\п в j-й отрасли ;	y j	- продукт труда в j-й отрасли
	p j			L		p j		L

Замкнутая статистическая модель Вальраса-Леонтьева.

Открытая статистическая модель Леонтьева: (E A)x y , p(E A) lw lx L . Замыкаем модель, предполагая, что y=y0L, где y0 – вектор фиксированных пропорций КП, то есть y –вектор заданной структуры. Получаем замкнутую статическую модель Леонтьева: (E A)x y0 L , p(E A) lw , lx L . Выполним некоторые преобразования: умножим обе части равенства p(E A) lw справа на x, получим p(E A)x lwx wlx . Итак, получили равенство py wL – закон Вальраса в узком смысле, где py – общая стоимость КП, wL – з/п по всем

отраслям. Этот закон утверждает, что весь произведенный продукт (в денежном выражении) тратится на потребление, то есть суммарный спрос = суммарному предложению. Существует также закон Вальраса в широком смысле: суммарное предложение суммарного спроса, то есть py wL.

24. Непрерывные и дискретные динамические модели Леонтьева. Замыкание динамических моделей Леонтьева. Определение технологического темпа прироста для непрерывной модели.

Пусть X = X(t) – вектор-столбец выпуска валового продукта (ВП) в материальном выражении в момент времени t, Y = Y(t) – вектор-столбец выпуска конечного продукта (КП) в материальном выражении в момент времени t,

C(t) – вектор-столбец непроизводственного потребления в материальном выражении в момент времени t, S(t) = I(t)) – вектор-столбец производственного накопления в материальном выражении в момент времени t.

Для чистого продукта предполагается выполненным баланс Y = S + C, где Y = X – AX. Напомним, что A = {aij} – матрица коэффициентов прямых материальных затрат. Она включает в себя также затраты на возмещение выбытия (амортизацию) и капитальный ремонт ОПФ. B = {bij} – матрица коэффициентов капиталоемкости приростов производства, матричный акселератор, где bij – затраты производственного накопления i-ой отрасли на единицу

	прироста валового продукта j-ой отрасли, то есть	S(t) B	dX (t)	.
			dt

а) Многопродуктовая открытая динамическая модель Леонтьева для ВП имеет вид: X (t) AX (t)

Пусть (E A)	1	0	, тогда X (E A)	1			(E A)	1
					Y , X				Y .

б) Многопродуктовая открытая динамическая модель Леонтьева для КП имеет вид:

	B	dX (t)
		dt

C(t)

.

Y (t) B(E A)	1	dY (t)	C(t) .
		dt

Замыкание динамической модели Леонтьева Замкнутые модели можно получить, записав зависимости

~ C CY

, где

	c
		1
		c
		2
	C
		0

cn

,

	s
		1
		s2
	S
		0

sn

.

Здесь c1, …, cn – нормы непроизводственного потребления по отраслям, s1, …, sn – нормы производственного

накопления по отраслям, c1 + s1 = 1, …, cn + sn = 1, то есть

C S E , Y = X – AX,

C C(E A)X

CY .

Для определения технологического темпа прироста будем искать решение системы однородных уравнений по

методу Эйлера, то есть, в виде

X (t)

X0e

t

, где X0

X (0) - начальное условие, - корень характеристического

уравнения det (E A B) 0

, корень характеристического уравнения det (E B(E A)

1

) 0 в случае

det (E A) 0 , собственное число матрицы (E A)

B

1

при det B 0 . Тогда в последнем случае

1

–

собственное число матрицы B(E A)

1

.

Если B 0, detB 0, A 0, A – неразложимая и продуктивная матрица, то B(E A)

1

0

– неразложимая

ˆ

ˆ

A)

1

)

0

матрица. Тогда по теореме Перрона-Фробениуса существует число Фробениуса s

s(B(E

неразложимой матрицы

B(E

A)	1

. Отсюда ˆ 1sˆ 0 – технологический темп прироста в межотраслевой

динамической модели Леонтьева. Причем, это самый меньший темп прироста по всем отраслям. Далее, из

ˆ	R,	ˆ	S	ˆ	ˆ	1 r ,	ˆ	ˆ	1 s .
неравенств r s		s s		следует: 1 R 1 s			1 S 1 s

Дискретные динамические модели Леонтьева. а) Модель для ВП:

X (t) AX (t) B X (t) = C(t), t = 0, 1, 2, …,

где X (t) X (t 1) X (t) , det B 0 . Проделав ряд преобразований, получим

X (t 1) DX (t) B	1
	C(t) ,

где D B 1 (E A B) E B 1(E A) .

б) Модель для КП:

Y (t) B(E A) 1 Y (t) C(t) ,

по-другому:

Y (t 1) FY (t) (E A)B 1C(t) , где F E (E A)B 1 .

Обозначим

		2n
Z	(u, v) R		,

25. Модели Гейла и Неймана. Теоремы о магистрали.

u 0, v 0 , – технологическое множество, множество технологических

способов производства, технологическая модель Гейла, где

n	, v R	n
u R

– векторы, u – вектор затрат, v – вектор

выпусков, причем u v, т.е. затраты обеспечивают выпуск. Поэтому такую модель называют моделью «затраты – выпуск». Иногда u и v разделены во времени, т.е. u переходит в v за промежуток времени: ut vt+1. Технологическое множество можно описать как некоторое подмножество конечномерного пространства Аксиомы технологического множества:

1)	(0, v) Z v 0 .
2) (u1, v1) Z,		(u2 , v2 ) Z
3)	(u, v) Z,	[0;1] (u,

4)Z – замкнутое множество в R2n.

5)i 1, ,n (u,v) z : vi

Модель Неймана.

(u1 u2 , v1 v2 ) Z – аддитивность.

v) ( u, v) Z	- бесконечная делимость технологического множества.
0 , где v (v1,	, vi , , vn ) , то есть любой продукт можно произвести.

Опишем подробнее модель Неймана.

возникают матрицы	1T	,	, a	mT
	A (a

Пусть ( ) и B

1		1
a	,b ),
	1T	,
(b

	, (a		m	,b	m	) – базисные технологические способы. Тогда
b	mT	)	и (u, v) Z u Ax,				v Bx , где x - вектор-столбец

интенсивностей использования технологий. Здесь «T» – символ транспортирования матрицы. В результате модель

Неймана может быть записана в виде Z {(u, v) : u Ax ,	v Bx ,	x 0} .
затраты	выпуск

Модель Леонтьева может быть рассмотрена как частный случай модели Неймана при

A = A, B = E, Z {(u, v) : u Ax ,

v x } .

затраты интенсивность выпуска

Для всех этих моделей вводится показатель

*

– темп роста модели Гейла:

*

max

(u,v) Z

*

*

*

*

*

v

i

по всем i, для которых ui

Доказано, что (u

, v ) :

(u

, v ) , где (u, v) min

u

i

задать магистраль v

*

*

*

. Взяв

*

*

*

*

*

(0)

*

(2)

(

*

)

2

*

(0),

u

u

(0) v

u

(1) u

, u

u

		v
	min		i	.
		u
	i
	i:u 0		i
	0	. Такое
		*	(n) (
	,u

*

*

позволяет

)	n	*	(0) .
		u

В результате получаем дискретный луч (луч Неймана) - это магистраль в модели Гейла, то есть траектория максимального пропорционального сбалансированного роста. Магистраль нужна для нахождения оптимальных в соответствующих смыслах траекторий, так как большую часть времени оптимальная траектория находится на магистрали.

Теоремы о магистрали В различных предположениях утверждения о существование магистрали (теоремы о магистрали) доказаны в трех

формах: слабой, сильной и сильнейшей. В слабых теоремах отмечено, что оптимальные траектории могут отклоняться от магистрали. Теоремы о магистрали в сильной форме утверждают, что отклонение от магистрали может приходиться только на начальном и конечном участках оптимальной траектории. Теоремы о магистрали в сильнейшей форме говорят, что большую часть времени оптимальные траектории находятся на магистрали.

Слабая теорема.

Сильная теорема

Сильнейшая теорема.