Конспект_ИЭЭ_14

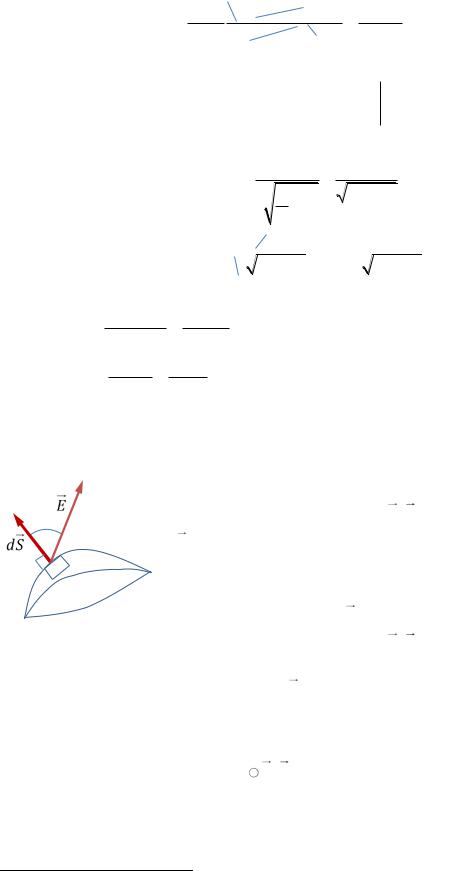
150

Подставим выражения для r и dl в выражение для dEx:

Q

2

Q

dE

bdα cos α cosα

cosαdα .

x

4πε l

2

2

4πε lb

cos α b

0

0

Проинтегрируем по α:

α0

Q

Q

α0

Qsinα0

Ex

cosαdα

sinα

4πε lb

4πε lb

2πε lb

α0

α

0

0

0

0

(стержень виден из точки C под углом 2α0). Из РИС. 19.4

sinα0

l

l

;

2

2

2

l

2

l

4b

4

b

E

Ql

Q

.

2πε b

2πε lb l2

4b2

l2

4b2

0

0

Предельные случаи

	а) b >> l E	Q
		2πε b 2b
		0

	б) b << l E	Q
		2πε bl
		0

гим способом ПОЗДНЕЕ.

		Q
		4πε
		0
		τ
	2πε b
		0

2	– поле точечного заряда.
b

– поле длинной нити. Эту формулу мы получим дру-

3.2.3. Поток векторного поля. Теорема Остроградского-Гаусса для напряжённости электрического поля

Элементарный поток

					dΦ EdS	,
	α	dS направлен по внешней47 нормали к малому участку dS;
	·			dΦ EdS cosα
	S	(см. РИС. 19.5).
		Полный поток вектора E сквозь поверхность S
	Рис. 19.5
					Φ EdS	.
					S
			E
	Теорема Остроградского-Гаусса для			: поток вектора напряжённости электри-

ческого поля сквозь произвольную замкнутую поверхность равен алгебраической сумме зарядов, охваченной этой поверхностью, делённой на ε0:

		.
EdS	q S
S	ε0

47 Если поверхность S не замкнута, то выбор одного из двух направлений нормали произволен, при этом направление нормали для всех участков dS должно быть одинаковым.

151

Доказательство48 (вывод из закона Кулона)

Рассмотрим точечный заряд q и его электрическое поле. Окружим заряд произвольной замкнутой поверхностью S (РИС. 19.6А). По закону Кулона напряжённость электрического поля точечного заряда

	E	q	r
		4πε	r	3
		0

.

S

q	α
	dΩ
	а

q	dΩ	α

б

Рис. 19.6

Элементарный поток

dΦ EdS

	qcosα		dS
	4πε r	2
	0

.

Телесный угол, под которым из точки, где находится заряд q, видна площадка dS

dΩ	dS		dS cosα
	r2		r2

(см. РИС. 19.6Б). Выразим элементарны й поток через телесный угол:

dΦ qdΩ .

4πε0

Проинтегрируем по полному телесному углу:

		4π			q 4π		q
	Φ EdS		qdΩ
			4πε		4πε		ε
	S	0
			0		0		0

.

Мы доказали теорему для случая одного точечного заряда. Обобщение на случай произвольной системы зарядов проводится по принципу суперпозиции полей:

E Ei

,

48 Мы строим курс, постулируя уравнения Максвелла. Это доказательство даётся для того, чтобы продемонстрировать связь уравнений Максвелла с эмпирическими законами электромагнетизма:

в данном случае – III уравнения Максвелла (теорема Остроградского-Гаусса для E ) и закона Кулона, и не входит в экзаменационную программу.

152

	EdS Ei dS EidS			i
				q
				ε
	S	S	S
				0

	q	S
	ε
	0

, ч. т. д.

Рассмотрим примеры расчёта полей с использованием теоремы ОстроградскогоГаусса для E . Эта теорема полезна в том случае, когда можно выбрать замкнутую поверхность так, чтобы легко было вычислить поток E . Прежде чем решать зада-

чу с помощью теоремы Остроградского-Гаусса, нужно найти направление E методом суперпозиций.

Случаи использования теоремы Остроградского-Гаусса
Сферическая	Цилиндрическая	Плоская
(центральная)	(осевая)	симметрия
симметрия	симметрия	распределения
распределения	распределения	заряда
заряда	заряда	(размеры области про-
	(протяжённость области	странства, содержащей за-
	пространства, содержащей	ряд, в плоскости симмет-
	заряд, вдоль оси симмет-	рии много больше попе-
	рии много больше её попе-	речного размера этой об-
	речных размеров)	ласти)

ПРИМЕРЫ

1) Электрическое поле равномерно заряженной сферы

				Сфера радиуса R равномерно заряжена за-
				рядом Q (РИС. 19.7). Найти зависимость
			I	напряжённости электрического поля от рас-
Q		II	SII	SI стояния r от центра сферы Er(r)49.
				Заряд распределён сферически симметрич-
		O	R	но. В каждой точке пространства напряжён-
				ность электрического поля E направлена
		r
	B			радиально.
			r	Будем выбирать поверхности интегрирова-
				ния в виде сфер радиуса r,где r – расстояние
			A	от центра сферы до точки, где измеряется
				напряжённость поля.
				Разобьём пространство на две области – вне
				сферы и внутри сферы. Вид зависимости
				Er(r) в этих областях должен быть различ-
		Рис. 19.7		ным.

49 Здесь и далее в подобных примерах мы находим именно проекцию векторного поля на указанное направление – величину, которая содержит информацию и о модуле, и о направлении векторного поля. В зависимости от знака заряда проекция напряжённости электрического поля может быть как положительной, так и отрицательной.

153

I. r > R

Теорема Остроградского-Гаусса:

EIdSI		q	S
				I
S		ε
	I	0

.

Выберем поверхность SI в виде сферы радиуса r, концентричной заряженной сфере (РИС. 19.7). В каждой точке этой поверхности (например, в точке A на рисунке)

напряжённость электрического поля EI

накова. Вектор внешней нормали

dSI

направлена радиально, а по модулю оди-

сонаправлен

EI

. Поток напряжённости

электрического поля

EIdSI EIrdSI cos0 EIr
S	I	S	I	1

Заряд, охваченный поверхностью SI,

q	S
	I
– весь заряд заряженной сферы. Получим

dSI SI

Q

E	Ir	S	I

EIr

4πr	2

.

E		4πr	2		Q
	Ir				ε
					0

E

Ir

		Q
		4πε r	2
		0

.

II. r < R

Теорема Остроградского-Гаусса:

		EIIdSII	q	S
					II	.
S			ε
	II		0

Выберем поверхность SII в виде сферы радиуса r, концентричной заряженной сфе-

ре (РИС. 19.7). Направления EII и dSII показаны на рисунке. Поток напряжённости электрического поля, аналогично выражению для области I,

EIIdSII SII

EIIr

4πr	2

.

Заряд, охваченный поверхностью SII,
q	S	0	,
	II

так как заряды внутрь поверхности SII не попадают. Поэтому

EIIr 0 .

График зависимости Er(r) представлен на РИС. 19.8.

При r = R график Er(r) терпит разрыв, так как на поверхности r = R сосредоточены свободные заряды. Разрывы конечной величины на графиках можно соединять сплошной линией.

S

Рис. 19.9

154

Er

0

R

r

Рис. 19.8

2) Электрическое поле равномерно заряженной бесконечно длинной тонкой прямой нити

			Бесконечно длинная прямая нить равно-
	τ		мерно заряжена с линейной плотностью
			τ (РИС. 19.9). Найти зависимость напря-
			жённости электрического поля от рас-
	B		стояния r от нити Er(r).
			Распределение заряда					имеет осевую
	r		симметрию. Теорема				Остроградского-
h			Гаусса
		A		EdS			q		S
						ε			.
			S				0

Выберем поверхность интегрирования в виде цилиндра радиуса r (r – расстояние от нити до точки, где измеряется поле – точка A на РИС. 19.9) и произвольной вы-

соты h, ось которого совпадает с нитью. Напряжённость электрического поля направлена радиально и зависит только от r. Векторы внешней нормали направ-

лены: для боковой поверхности dSбок

E , для торцов

dSторц

E

. Поток напряжён-

ности электрического поля					1				0
								π
EdS		EdSбок 2		EdSторц ErdSбок cos0 2			ErdSторц cos
S	Sбок	Sторц		Sбок	Sторц			2

Er dSбок Er Sбок Er 2πrh.

Sбок

Заряд, охваченный поверхностью S,

q S τh

– заряд участка нити длиной h. Получим

E	2πrh τh	E			τ	.
			r
r	ε				2πε r
	0				0

155

Результат не зависит от h, как и должно быть. Это же решение было получено нами методом суперпозиций (см. РАЗДЕЛ 3.2.3).

График зависимости Er(r) представлен на РИС. 19.10.

Er

0

r

Рис. 19.10

156

Лекция 20

3.2.3. Поток векторного поля. Теорема Остроградского-Гаусса для напряжённости электрического поля (продолжение)

3) Электрическое поле равномерно заряженной плоскости

Плоскость равномерно заряжена с поверхностной плотностью σ. Найти зависимость напряжённости электрического поля от расстояния от плоскости: Ex(x).

σ

C

B A

S

0

x

Рис. 20.1

Распределение заряда имеет плоскую симметрию. Теорема Остроградского-Гаусса

	q
EdS		S
	ε	.
S
	0

Выберем поверхность интегрирования в виде цилиндра высотой

2 x

(x – коорди-

ната точки, где измеряется поле, – точки A на РИС. 20.1) и произвольного сечения Sторц, расположенного симметрично относительно заряженной плоскости. Напряжённость электрического поля направлена перпендикулярно плоскости и может зависеть только от x. Векторы внешней нормали направлены: для боковой по-

верхности dSбок E , для торцов поля

dSторц

E

. Поток напряжённости электрического

EdS EdSбок 2			EdSторц	ExdSбок cos	π	2	ExdSторц x cos0
S	Sбок	Sторц	Sбок		2	Sторц

2E dSторц 2ESторц .

Sторц

Заряд, охваченный поверхностью S,

q S σSторц

– заряд участка плоскости площадью Sторц. Получим

157

			σS
2ES			торц
	торц		ε
			0
		x 0:E
				x
		x 0:E
				x

E

σ , 2ε0

σ

2ε0

σ 2ε0

.

50;

По каждую сторону от заряженной плоскости поле однородно. График зависимости Ex(x) представлен на РИС. 20.2.

Ex

0

x

Рис. 20.2

Демонстрация: Сетка Кольбе

3.2.4. Потенциал

I уравнение Максвелла для электростатического поля

Edl

L

0

.

Умножим это уравнение на пробный заряд q0:

0		Edl		0		1
q				q Edl		F dl 0
	L		L		L

– работа электростатического поля по перемещению пробного заряда по произвольной замкнутой траектории равна нулю. Это означает, что электростатиче-

ское поле потенциально (см. РАЗДЕЛ 1.8.4).

[Можно прийти к этому выводу по-другому: кулоновская сила центральна, а поле центральных сил потенциально (см. 1.8.4).]

Потенциальная энергия заряженной частицы в электростатическом поле равна работе внешних сил при перемещении этой частицы из точки, где потенциальная энергия принята равной нулю, в данную точку, или работе поля при этом перемещении:

Wп Aполя A* .

Потенциальная энергия – характеристика и поля, и заряда:

50 Эта формула справедлива при σ > 0. Для σ < 0 знак σ нужно изменить на противоположный.

158

	Отношение	W
		п
		q
		0
	ля:

– потенциал;

Wп f q0 ,E .

не зависит от q0 и является энергетической характеристикой по-

	φ	W
		п	;
		q
		0

[φ] = В (вольт).

Эта величина определяется с точностью до произвольной постоянной. Физиче-

ский смысл имеет разность потенциалов

				поля		*
	φ	φ φ		A		A
				1 2		1 2
	12	2	1	q		q
				0		0

– работа поля по перемещению пробного заряда из начального положения в конечное, отнесённая к модулю этого заряда и взятая с обратным знаком, или работа внешних сил при том же перемещении, отнесённая к модулю пробного заряда.

Связь напряжённости и потенциала электростатического поля

Работа электростатического поля при перемещению пробного заряда из точки 1 в точку 2

		2	1	2	0	0	2
поля			F dl		q Edl q			Edl
A
		1		1			1

разность потенциалов

;

			поля	2
	φ12		A	Edl ;
			q0
				1

интегрирование проводится по произвольной кривой, соединяющей точки 1 и 2.

Интегральная связь напряжённости и потенциала электростатического поля

				2			2
		φ			Edl			E	dl		,
		12						l
				1			1
1			1				1		l
				Edl
φ									E	dl
			φ 0			φ 0

– потенциал поля в точке 1. Элементарная работа поля

δAполя F1dl q0Edl ;

элементарное приращение потенциала

dφ	δAполя	Edl ,
	q
	0

		159
	E	dφ	gradφ
		dl

– дифференциальная связь напряжённости и потенциала электростатиче-

	ского поля (определение вектора градиента φ	dφ	см. в РАЗДЕЛЕ 1.8.5).
		dl

Эквипотенциальная поверхность – геометрическое место точек, потенциал которых одинаков.

Так как

E gradφ , вектор напряжённости электрического поля перпендикуля-

рен эквипотенциальным поверхностям.

ПРИМЕР

Потенциал поля точечного заряда

Напряжённость электрического поля точечного заряда q

	E	q	r		.
		4πε	r	3
		0

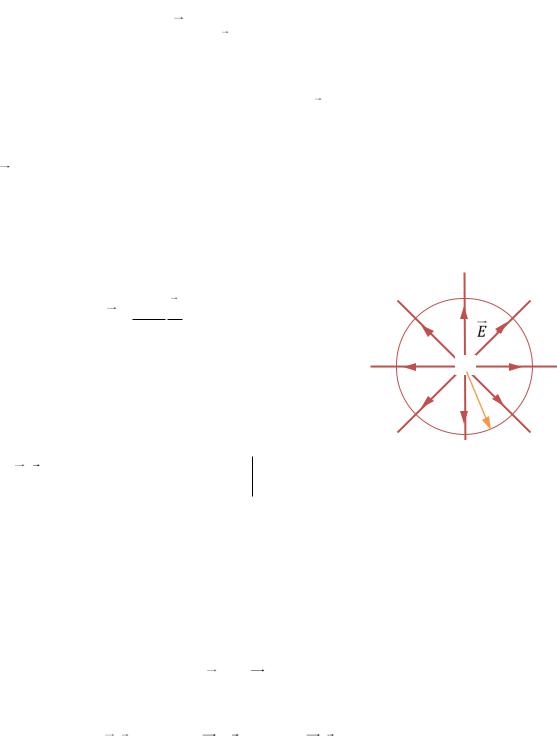
Эквипотенциальные поверхности – сферы (РИС. 20.3).

Положим начало отсчёта потенциала в бесконечно удалённой точке: φ(∞) = 0. Интегрирование в формуле интегральной связи напряжённости и потенциала проведём по радиальной прямой:

	r	r	r	q	dr2	q	1	r	q
	φ Edr Erdr									.
				4πε		4πε	r		4πε r
					r
				0		0			0

q

r

Рис. 20.3

Принцип суперпозиции (в применении к потенциалу): потенциал электростатического поля системы заряженных тел равен сумме потенциалов полей, создаваемых каждым из этих тел по отдельности:

φ φ	, φ		dφ	.
i

Доказательство

Имеем систему N заряженных тел. По принципу суперпозиции напряжённость электрического поля

E Ei .

Интегральная связь напряжённости и потенциала для поля в точке A

A

A

i

A

i

i

φ

Edl

dl

dl

E

E

φ

φ 0

φ 0

φ 0

, ч. т. д.

Любую систему заряженных тел можно разбить на точечные заряды и найти потенциал по методу суперпозиций. Таким образом проще рассчитать потенциал, чем напряжённость электрического поля, так как потенциал – скалярная величина, а напряжённость – векторная.