Тема 9. Законы распределения случайных величин

9.1. Случайная величина ξ имеет биномиальное распределение с параметрами n и p (n – натуральное число, 0  p  1), если она принимает значения 0, 1, … , n с вероятностями .

Заметим, что характеристическое свойство (7.1) (см. тему 7) выполняется, так как в силу формулы бинома Ньютона .

Биномиальное распределение является распределением числа “успехов” в n испытаниях Бернулли с вероятностью “успеха” p и “неудачи” q = 1 – p в каждом испытании (см. тему 6).

Математическое ожидание и дисперсия с.в. ξ: M = np, D = npq.

Максимум вероятностей p_k (k = 0, 1, … , n) достигается при k = [np – q] + 1, которое называется наиболее вероятным (или наивероятнейшим) числом “успехов” в n испытаниях Бернулли. Здесь [x] – целое число от x.

9.2. Случайная величина ξ имеет гипергеометрическое распределение с параметрами N, M, n (N, M, n – натуральные числа, M  N, n  N), если она принимает значения m₀, m₀ + 1, m₀ + 2, … , m₁, с вероятностями где

m₀ = max (0, N – M + n), m₁ = min (M, n).

Гипергеометрическое распределение является распределением числа объектов, обладающих заданным свойством среди n объектов, случайным образом извлеченных (без возвращения) из совокупности N объектов, из которых M обладают этим свойством (см. тему 2).

Математическое ожидание и дисперсия с.в. ξ: .

9.3. Случайная величина ξ имеет геометрическое распределение с параметром p (0 < p < 1), если она принимает значения 1, 2, … , n, …. (счетное множество значений) с вероятностями

.

Воспользовавшись формулой суммы бесконечно убывающей геометрической прогрессии, убеждаемся, что характеристическое свойство (7.1) (см. тему 7) выполняется:

.

Геометрическое распределение является распределением числа испытаний Бернулли до появления первого “успеха”, если вероятность “успеха” в каждом испытании равна p.

Математическое ожидание и дисперсия с.в. ξ:

.

9.4. Случайная величина ξ имеет распределение Пуассона с параметром  ( > 0), если она принимает значения 0, 1, … , n, …. (счетное множество значений) с вероятностями

.

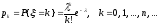Характеристическое свойство (7.1) снова выполнено, так как

.

Распределение Пуассона является пределом биномиального распределения, когда в схеме Бернулли n   и p  0 так, что np =  > 0. Поскольку при этом вероятность “успеха” p мала, то распределение Пуассона часто называют законом распределения редких событий.

Математическое ожидание и дисперсия с.в. ξ совпадают:

M = D = .

9.5. Случайная величина ξ имеет равномерное распределение на отрезке [a, b], где a < b, если её плотность распределения p(x) постоянна на этом отрезке и равна нулю вне его:

Функция распределения с.в. ξ, распределенной по равномерному закону на отрезке [a, b], имеет вид

Графики функций p(x) и F(x) приведены на рис. 9.1.

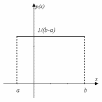
Рис.9.1. Плотность и функция распределения равномерного закона

Математическое ожидание и дисперсия равномерно распределенной с.в. ξ:

.

9.6. Случайная величина ξ имеет показательное (или экспоненциальное) распределение с параметром  ( > 0), если её плотность распределения p(x) имеет вид

Функция распределения с.в. ξ, распределенной по показательному закону, равна

Графики функций p(x) и F(x) приведены на рис. 9.2.

Рис.9.2. Плотность и функция распределения показательного закона

Математическое ожидание и дисперсия показательно распределенной с.в. ξ:

.

9.7. Случайная величина ξ имеет нормальное распределение с параметрами a и  (–  < a < ,  > 0), если её плотность распределения p(x) выражается формулой

,

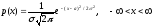а функция распределения

,

где – функция Лапласа (см. тему 6).

Подчиненность с.в.  нормальному закону распределения с параметрами a и  символически обозначается   N(a, ).

Графики функций p(x) и F(x) приведены на рис. 9.3.

Рис.9.3. Плотность и функция распределения нормального закона

Математическое ожидание с.в., распределенной по нормальному закону, равно параметру a, дисперсия равна ²:

M = a, D = ².

Нормальное распределение при a = 0 и  = 1 называется стандартным нормальным. Плотность и функция распределения этого закона распределения равны соответственно

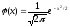и , – < x < .

Теорема. Пусть с.в.   N(a, ) и <х₁, х₂> один из интервалов (конечный или бесконечный) вида [х₁, х₂], [х₁, х₂), (х₁, х₂], (х₁, х₂). Тогда

1) ;

2) 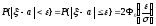для любого числа  > 0.

13