3. Моделирование стационарных случайных процессов

Цель работы: освоение методов моделирования случайных процессов с заданными спектрально-корреляционными свойствами.

1. Основные теоретические сведения

При моделировании систем управления и обработки информации важно уметь формировать модели внешних воздействий и ошибок измерений, представляемых, как правило, стационарными случайными процессами с заданными корреляционными функциями R() или спектральными плотностями S(). Как известно, данные статистические характеристики связаны между собой прямым и обратным преобразованиями Фурье:

Для того, чтобы получить стационарный процесс с заданными характеристиками, обычно используют метод формирующего фильтра [1], рассчитывая его таким образом, чтобы при подаче на вход фильтра процесса (t) типа белого шума его выходной сигнал y(t) обладал необходимыми свойствами. Отметим, что при моделировании марковских случайных процессов, характеризуемых спектральной плотностью дробно-рационального вида, формирующий фильтр будет линейным. Для получения передаточной функции W_фф(p) такого фильтра спектральную плотность процесса подвергают факторизации, т.е. представляют ее в виде произведения двух комплексно сопряженных сомножителей, все нули и полюса первого из которых лежат в левой полуплоскости, а второго – в правой:

Здесь предполагается, что интенсивность порождающего белого шума (t) равна единице.

Модель формирующего фильтра, заданная его передаточной функцией, может быть также представлена в форме пространства состояний [4]:

(13)

где x – вектор состояния фильтра; F – матрица динамики; G – матрица возмущений; H – матрица наблюдения.

Начальное состояние фильтра x(0) должно быть сформировано таким образом, чтобы обеспечить стационарность выходного процесса. Это условие выполняется, если ковариационная матрица P вектора состояния в начальный момент времени соответствует ее установившемуся значению, которое может быть найдено из матричного уравнения [5]

(14)

Заметим, что решение уравнения (14) может быть легко получено, если числитель дробно-рациональной спектральной плотности S() не зависит от . В этом случае процесс является n – 1 раз дифференцируемым, где n – порядок фильтра, так что переменные состояния могут быть выбраны равными соответственно выходному моделируемому процессу и его производным до (n – 1)-й включительно: x₁ = y ; x₂ = y^˙, …, x_n = y^{(n – 1)}. Действительно, в этом случае, как следует из вида функции S(), уравнение фильтра не будет содержать производных входного процесса, а n-я производная выходного процесса x^˙_n = y⁽ⁿ⁾ может быть выражена через его младшие производные y, y^˙, …, y^{(n – 1)}, т.е. непосредственно через переменные состояния x₁, x₂, …, x_n. Таким образом, элементы матрицы P, удовлетворяющие условию (14), могут быть сформированы только лишь исходя из выражения для корреляционной функции моделируемого процесса.

К примеру, для фильтра второго порядка имеем y = x₁; x^˙₁ = x₂. В этом случае матрица ковариаций, соответствующая стационарному векторному процессу x(t), примет вид [3]

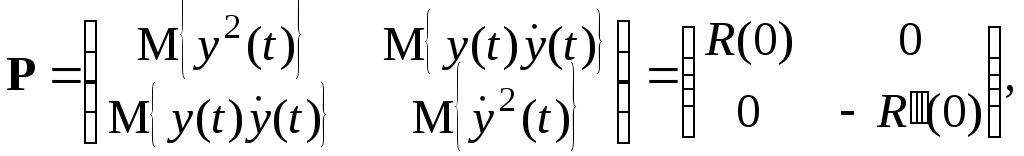
причем R(0) = R(+0) = R(–0), т.е. при вычислении производных достаточно для определенности положить  > 0.

Соответственно, для фильтра третьего порядка y = x₁; x^˙₁ = x₂; x^˙₂ = x₃;

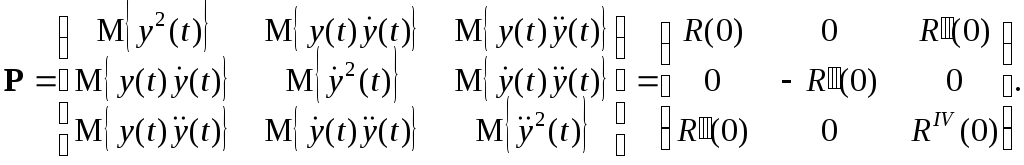
Начальное состояние фильтра формируется в виде x(0) = C, где CC^T = P,  – центрированная случайная величина с единичной дисперсией. При этом если матрица P диагональная, матрица C будет также диагональной с элементами C_ii =  в противном случае для нахождения матрицы C можно воспользоваться, например, разложением Холецкого [6], которое реализуется в Matlab с помощью встроенной функции chol.

Поскольку при компьютерном моделировании случайный процесс неизбежно должен быть представлен своими дискретными отсчетами, от непрерывной модели (13) переходят к ее дискретному описанию [4]:

(15)

где w_k – дискретный белый шум с дисперсией Q. Матрицы  и  следует определить из условия стохастической эквивалентности моделей (13) и (15), состоящей в совпадении математического ожидания и матрицы ковариаций вектора x(t), соответствующего непрерывной модели (13), с математическим ожиданием и матрицей ковариаций вектора x_k, соответствующего дискретной модели (15), в моменты времени t_k = kt, где t – период дискретности.

Поскольку матрица ковариаций P_k дискретной последовательности x_k определяется с помощью рекуррентного соотношения [5]

а для матрицы ковариаций P(t_k) непрерывного процесса x(t), t = t_k, справедливо следующее соотношение, являющееся следствием формулы Коши [4]:

,

где () = e^F – фундаментальная матрица системы (13), то условие стохастической эквивалентности может быть выполнено путем выбора матриц ,  и дисперсии Q в соответствии с соотношениями

 = e^Ft ≈ E + Ft, (16)

(17)

Здесь E – единичная матрица.

На практике для нахождения  и Q нередко используют различного рода приближенные процедуры. Так, в первом приближении (при малых t) e^F ≈ E + F, и равенство (17) принимает вид

Полагая

 = Gt (18)

(что совпадает с формулой первого приближения для кусочно-постоянных входных воздействий [4]), для дисперсии порождающего шума получим Q = 1/t.

Период дискретности t следует выбирать таким образом, чтобы он был много меньше самой малой постоянной времени формирующего фильтра: при формировании узкополосных процессов t << 1/, где  – преобладающая частота процесса; при формировании широкополосных процессов t << 1/, где  – ширина спектра.