2.2. Модальный синтез
Модальный синтез предполагает формирование таких обратных связей по состоянию, при которых обеспечивается заданное расположение полюсов замкнутой системы.
Рассмотрим уравнения состояния замкнутой системы
На рис. 2.1 приведена структура, соответствующая этим уравнениям.
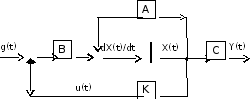
Рис. 2.1. Система с обратной связью по состоянию
Свободное движение системы (при g(t) = 0) описывается выражением:
где K – вектор коэффициентов обратной связи.
Основная теорема модального управления гласит, что если линейная динамическая система является управляемой, то линейная обратная связь может быть выбрана таким образом, что матрица (А – ВK) будет иметь желаемый спектр (желаемое расположение полюсов замкнутой системы).
При доказательстве этой теоремы используется каноническая форма управляемости. Рассмотрим одномерную систему с вектором обратной связи
Заданному спектру соответствует характеристический полином замкнутой системы
Этому полиному можно поставить в соответствие каноническую форму матрицы замкнутой системы
Рассматривая канонические формы матриц А и В исходной системы, можно записать:
Откуда следует:
Последняя формула справедлива при любых параметрах, поэтому теорему можно считать доказанной.
Пример 2.6. Модальный синтез для системы со скалярным входом.
Матрица управляемости
Определитель не равен нулю, следовательно, система является полностью управляемой.
Характеристическое уравнение:
Коэффициенты уравнения α0 = 2, α1 = –3.
Оба полюса положительные (λ1=2, λ2=1), следовательно, система является неустойчивой.
Зададим желаемые полюса замкнутой системы:
λ1* = –1, λ2* = –3.
Характеристическое уравнение желаемой замкнутой системы имеет вид:
Коэффициенты уравнения β0 = 3, β1 = 4.
Таким образом, коэффициенты обратной связи:
k1 = β0 – α0 = 3 – 2 = 1,
k2 = β1 – α1 = 4 – (–3) = 7.
Уравнения состояния:
Этим уравнениям соответствует структурная схема, показанная на рис. 2.2.
Рис. 2.2. Пример регулятора по состоянию
2.3. Формула Аккермана
Таким образом, для решения задачи модального управления можно перевести модель произвольной структуры в каноническую форму управляемости, после чего с помощью уравнения получить коэффициенты обратной связи. Однако в реальной системе желательно использовать переменные состояния, отражающие физическую сторону протекающих процессов, а не абстрактные переменные состояния канонической формы, которые могут быть недоступны для измерения. Аккерманом была предложена формула, позволяющая с помощью преобразования подобия перевести модель произвольной структуры в каноническую форму управляемости, определить искомые коэффициенты K, а затем пересчитать полученное решение применительно к исходной структуре.
Если задан желаемый характеристический полином замкнутой системы
q(s)
=
,
то формула Аккермана имеет вид:
Пример 2.7. Пусть система описывается матрицами
Желаемые полюса заданы вектором
.
Требуется найти коэффициенты обратной связи.
Характеристический полином желаемой замкнутой системы имеет вид:
q(s)
=
,
т. е. a2=3; a1=4.
Формула Аккермана:
Этот результат совпадает с полученным ранее.
Пример 2.8. Дана передаточная функция объекта:
Найти коэффициенты обратной связи, обеспечивающие заданные значения корней характеристического полинома замкнутой системы:
Запишем уравнения в канонической форме управляемости
Здесь, очевидно,
b2=0, b1=0, b0=10.
a2=16, a1=0, a0=1.
Тогда
Характеристическое уравнение желаемой замкнутой системы имеет вид:
Коэффициенты уравнения α0 = 2, α1 = 3.
Записываем формулу Аккермана
