
Ответы по математическому анализу
Таблица
эквивалентных бесконечно малых при ![]()
Как
показывает приведённый выше, пределы
отношения бесконечно малых можно
упрощать, откидывая бесконечно малые
слагаемые большего порядка и заменяя
множители в числителе и знаменателе на
эквивалентные бесконечно малые. Для
того, чтобы этот способ вычисления
пределов (точнее, раскрытия неопределённостей
вида ![]() )
можно было применять к возможно большему
числу примеров, мы должны иметь достаточно
большой запас известных пар эквивалентных
бесконечно малых величин. Для наиболее
употребительной базы
)
можно было применять к возможно большему
числу примеров, мы должны иметь достаточно
большой запас известных пар эквивалентных
бесконечно малых величин. Для наиболее
употребительной базы ![]() создадим
такой запас в виде таблицы "стандартных"
эквивалентных бесконечно малых.
создадим
такой запас в виде таблицы "стандартных"
эквивалентных бесконечно малых.
Поскольку
в этой таблице мы всегда будем рассматривать
базу ![]() ,
для простоты записи обозначение этой
базы будем пропускать и писать
знак
,
для простоты записи обозначение этой
базы будем пропускать и писать
знак ![]() вместо
вместо ![]() .
.
1) ![]() .
Эту формулу мы уже доказали и использовали
в примерах. Эквивалентность
.
Эту формулу мы уже доказали и использовали
в примерах. Эквивалентность ![]() и
и ![]() при
при ![]() означает
в точности, что первый замечательный
предел равен 1.
означает
в точности, что первый замечательный
предел равен 1.
2) ![]() .
Эта эквивалентность тоже была доказана
выше в одном из примеров.
.
Эта эквивалентность тоже была доказана
выше в одном из примеров.
3) ![]() .
Докажем эту эквивалентность:
.
Докажем эту эквивалентность:

4) ![]() .
Докажите это в качестве упражнения,
сделав замену
.
Докажите это в качестве упражнения,
сделав замену ![]() и
применив предыдущую табличную формулу.
и
применив предыдущую табличную формулу.
5)  .
Для доказательства воспользуемся
формулой
.
Для доказательства воспользуемся
формулой ![]() .
Далее, имеем:
.
Далее, имеем:
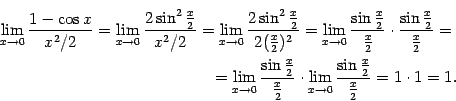
Это означает, что доказываемая эквивалентность имеет место.
6) ![]() (
( ![]() ).
Для доказательства этой эквивалентности
сделаем такое преобразование:
).
Для доказательства этой эквивалентности
сделаем такое преобразование:

Для вычисления предела правой части воспользуемся непрерывностью логарифма и вторым замечательным пределом:
![]()
и мы доказали формулу 6.
В
частном случае, при ![]() ,
получаем эквивалентность
,
получаем эквивалентность
![]() )
) ![]() .
.
7) ![]() (
( ![]() ).
Для доказательства сделаем замену
).
Для доказательства сделаем замену ![]() и
выразим
и
выразим ![]() через
через ![]() :
: ![]() .
Согласно формуле 6,
.
Согласно формуле 6, ![]() при
при ![]() ,
откуда
,
откуда ![]() .
Из непрерывности логарифма следует,
что
.
Из непрерывности логарифма следует,
что ![]() и,
значит,
и,
значит, ![]() при
при ![]() .
В этой формуле осталось лишь сменить
обозначение переменного
.
В этой формуле осталось лишь сменить
обозначение переменного ![]() на
на ![]() ,
чтобы получить формулу 7.
,
чтобы получить формулу 7.
В
частном случае, при ![]() ,
получаем эквивалентность
,
получаем эквивалентность
![]() )
) ![]() .
.
Сведём
теперь полученные формулы в итоговую
таблицу. Всюду в ней ![]() .
.
|
1) |
|
|
2) |
|
|
3) |
|
|
4) |
|
|
5) |
|
|
6) |
|
|
|
|
|
7) |
|
|
|
|
Приведём
примеры применения табличных формул
для раскрытия неопределённостей вида ![]() .
.
Пример 2.37
Вычислим предел  .
Для этого в числителе вынесем за скобку
.
Для этого в числителе вынесем за скобку ![]() ,
а к знаменателю применим формулу
,
а к знаменателю применим формулу  ,
где
,
где ![]() ,
, ![]() .
Получим
.
Получим
![]()
Мы
заменили ![]() на
эквивалентную величину
на
эквивалентную величину ![]() (учтя
при этом, что
(учтя
при этом, что ![]() при
при ![]() ),
), ![]() на
эквивалентную величину
на
эквивалентную величину ![]() (учтя,
что
(учтя,
что ![]() при
при ![]() ),
затем сократили числитель и знаменатель
на
),
затем сократили числитель и знаменатель
на ![]() и,
наконец, воспользовались тем, что
функции
и,
наконец, воспользовались тем, что
функции ![]() и
и ![]() непрерывны
и что
непрерывны
и что ![]() и
и ![]() .
.
Пример 2.38
Вычислим предел 
Заменим
в числителе ![]() на
эквивалентную величину
на
эквивалентную величину ![]() ,
а знаменатель
,
а знаменатель ![]() --
на эквивалентную величину
--
на эквивалентную величину ![]() .
После этого можно будет сократить дробь
на
.
После этого можно будет сократить дробь
на ![]() и
получить ответ:
и
получить ответ:

Ещё
раз обратим внимание читателя, что все
формулы таблицы эквивалентных бесконечно
малых относятся к базе ![]() .
Следовательно, те же эквивалентности
имеют место и при односторонних
базах
.
Следовательно, те же эквивалентности
имеют место и при односторонних
базах ![]() и
и ![]() .
Если же рассматриваемый пример содержит
неопределённость вида
.
Если же рассматриваемый пример содержит
неопределённость вида ![]() при
какой-либо другой базе, то часто предел
можно свести к пределу при "стандартной"
базе
при
какой-либо другой базе, то часто предел
можно свести к пределу при "стандартной"
базе ![]() (или
(или ![]() ,
или
,
или ![]() )
с помощью подходящей замены переменной,
а затем воспользоваться табличными
эквивалентностями.
)
с помощью подходящей замены переменной,
а затем воспользоваться табличными
эквивалентностями.
Пример 2.39
Вычислим предел  .
.
Если
сделать замену ![]() ,
то при
,
то при ![]() новая
переменная
новая
переменная ![]() будет,
очевидно, стремиться к 0, то есть
база
будет,
очевидно, стремиться к 0, то есть
база ![]() перейдёт
при такой замене в "стандартную"
базу
перейдёт
при такой замене в "стандартную"
базу ![]() .
Подставляя
.
Подставляя ![]() и
учитывая формулу приведения для косинуса,
получаем:
и
учитывая формулу приведения для косинуса,
получаем:

Мы
применили табличную формулу  ,
а затем сократили дробь на
,
а затем сократили дробь на ![]() и
получили ответ.
и
получили ответ.
Применяя формулы таблицы эквивалентностей бесконечно малых последовательно, мы можем получать (и использовать для вычисления пределов) цепочки эквивалентностей произвольной длины.
Пример 2.40 Можно, например, получить следующую формулу:

Здесь мы последовательно воспользовались формулами

и
учли, что величины ![]() ,
, ![]() ,
, ![]() ,
, ![]() являются
бесконечно малыми при
являются
бесконечно малыми при ![]() .
.
Используя полученную в результате эквивалентность
![]()
|
Бесконечно малая — числовая функция или последовательность, которая стремится к нулю. |
Бесконечно большая — числовая функция или последовательность, которая стремится к бесконечности определённого знака.
ЧИСЛОВАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ
ЧИСЛОВАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ – функция вида y = f(x), x О N,где N – множество натуральных чисел (или функция натурального аргумента), обозначается y = f(n) или y1, y2,…, yn,…. Значения y1, y2, y3,…называют соответственно первым, вторым, третьим, … членами последовательности.
Например, для функции y = n2\shad \shad0можно записать:
y1 = 12 = 1;
y2 = 22 = 4;
y3 = 32 = 9;…yn = n2;…\shad
\shad0
Способы задания последовательностей.
Последовательности можно задавать различными способами, среди которых особенно важны три: аналитический, описательный и рекуррентный.
1. Последовательность задана аналитически, если задана формула ее n-го члена:
yn = f(n).
Пример. yn = 2n – 1 – последовательность нечетных чисел: 1, 3, 5, 7, 9, …
2. Описательный способ задания числовой последовательности состоит в том, что объясняется, из каких элементов строится последовательность.
Пример 1. «Все члены последовательности равны 1». Это значит, речь идет о стационарной последовательности 1, 1, 1, …, 1, ….
Пример 2. «Последовательность состоит из всех простых чисел в порядке возрастания». Таким образом, задана последовательность 2, 3, 5, 7, 11, …. При таком способе задания последовательности в данном примере трудно ответить, чему равен, скажем, 1000-й элемент последовательности.
3. Рекуррентный способ задания последовательности состоит в том, что указывается правило, позволяющее вычислить n-й член последовательности, если известны ее предыдущие члены. Название рекуррентный способ происходит от латинского слова recurrere – возвращаться. Чаще всего в таких случаях указывают формулу, позволяющую выразить n-й член последовательности через предыдущие, и задают 1–2 начальных члена последовательности.
Пример 1. y1 = 3; yn = yn–1 + 4, если n = 2, 3, 4,….
Здесь y1 = 3; y2 = 3 + 4 = 7; y3 = 7 + 4 = 11; ….
Можно видеть, что полученную в этом примере последовательность может быть задана и аналитически: yn = 4n – 1.
Пример 2. y1 = 1; y2 = 1; yn = yn–2 + yn–1 , если n = 3, 4,….
Здесь: y1 = 1; y2 = 1; y3 = 1 + 1 = 2; y4 = 1 + 2 = 3; y5 = 2 + 3 = 5; y6 = 3 + 5 = 8;
Последовательность,
составленную в этом примере, специально
изучают в математике, поскольку она
обладает рядом интересных свойств и
приложений. Ее называют последовательностью
Фибоначчи – по имени итальянского
математика 13 в. Задать последовательность
Фибоначчи рекуррентно очень легко, а
аналитически – очень трудно. n-е
число Фибоначчи выражается через его
порядковый номер следующей формулой .
.
На первый взгляд, формула для n-го числа Фибоначчи кажется неправдоподобной, так как в формуле, задающей последовательность одних только натуральных чисел, содержатся квадратные корни, но можно проверить «вручную» справедливость этой формулы для нескольких первых n.
Свойства числовых последовательностей.
Числовая последовательность – частный случай числовой функции, поэтому ряд свойств функций рассматриваются и для последовательностей.
Определение. Последовательность {yn} называют возрастающей, если каждый ее член (кроме первого) больше предыдущего:
y1 < y2 < y3 < … < yn < yn+1 < ….
Определение. Последовательность {yn} называют убывающей, если каждый ее член (кроме первого) меньше предыдущего:
y1 > y2 > y3 > … > yn > yn+1 > … .
Возрастающие и убывающие последовательности объединяют общим термином – монотонные последовательности.
Пример 1. y1 = 1; yn = n2\shad \shad0– возрастающая последовательность.
Пример
2. y1 = 1; ![]() –
убывающая последовательность.
–
убывающая последовательность.
Пример
3. y1 = 1; ![]() –
эта последовательность не является не
возрастающей не убывающей.
–
эта последовательность не является не
возрастающей не убывающей.
Определение. Последовательность называется периодической, если существует такое натуральное число T, что начиная с некоторого n, выполняется равенство yn = yn+T . Число T называется длиной периода.
Пример.
Последовательность ![]() периодична
с длиной периода T= 2.
периодична
с длиной периода T= 2.
Арифметическая прогрессия.
Числовую последовательность, каждый член которой, начиная со второго, равен сумме предыдущего члена и одного и того же числа d, называют арифметической прогрессией, а число d – разностью арифметической прогрессии.
Таким образом, арифметическая прогрессия – это числовая последовательность {an}, заданная рекуррентно соотношениями
a1 = a, an = an–1 + d (n = 2, 3, 4, …)
(a и d – заданные числа).
Пример. 1, 3, 5, 7, 9, 11, … – возрастающая арифметическая прогрессия, у которой a1 = 1, d = 2.
Пример. 20, 17, 14, 11, 8, 5, 2, –1, –4,… – убывающая арифметическая прогрессия, у которой a1 = 20, d = –3.
Нетрудно найти явное (формульное) выражение an через n. Величина очередного элемента возрастает на d по сравнению с предыдущим, таким образом, величина n элемента возрастет на величину (n – 1)d по сравнению с первым членом арифметической прогрессии, т.е.
an = a1 + d(n – 1).
Это формула n-го члена арифметической прогрессии.
Используя явное выражение an через n, можно доказать следующее свойство арифметической прогрессии: если натуральные числа i, j, k, lтаковы, что i + j = k + l, то ai + aj= ak + al. Чтобы в этом убедиться, достаточно подставить i, j, k и l вместо n в формулу n-го члена арифметической прогрессии и сложить. Отсюда следует, что если рассматривать первые n членов арифметической прогрессии, то суммы членов, равно отстоящих от концов, будут одинаковы:
a1 + an = a2 + an–1 = a3 + an–2 = … = 2a1 + (n – 1)d.
Последнее равенство позволяет вычислить сумму первых n членов арифметической прогрессии:
Sn = a1 + a2 + … + an–1 + an.
С этой целью берется еще одна такая же сумма, но слагаемые записывается в обратном порядке:
Sn = an + an–1 + … + a2 + a1.
Далее она складывается почленно с исходной суммой, причем слагаемые сразу попарно группируются. В результате
2Sn = (a1 + an) + (a2 + an–1) + … + (an + a1) = n(2a1 + (n – 1)d),
откуда ![]() .
Это формула суммы n членов
арифметической прогрессии.
.
Это формула суммы n членов
арифметической прогрессии.
Арифметической прогрессия названа потому, что в ней каждый член, кроме первого, равен среднему арифметическому двух соседних с ним – предыдущего и последующего. Действительно, так как
an = an–1 + d;
an = an+1 – d.
Сложение
двух последних равенств дает ![]() .
.
Таким образом, верна следующая теорема (характеристическое свойство арифметической прогрессии). Числовая последовательность является арифметической тогда и только тогда, когда каждый ее член, кроме первого (и последнего в случае конечной последовательности), равен среднему арифметическому предшествующего и последующего членов.
Пример. При каком значении x числа 3x + 2, 5x – 4 и 11x + 12 образуют конечную арифметическую прогрессию?
Согласно характеристическому свойству, заданные выражения должны удовлетворять соотношению
5x – 4 = ((3x + 2) + (11x + 12))/2.
Решение этого уравнения дает x = –5,5. При этом значении x заданные выражения 3x + 2, 5x – 4 и 11x + 12 принимают, соответственно, значения –14,5, –31,5, –48,5. Это – арифметическая прогрессия, ее разность равна –17.
Геометрическая прогрессия.
Числовую последовательность, все члены которой отличны от нуля и каждый член которой, начиная со второго, получается из предыдущего члена умножением на одно и то же число q, называют геометрической прогрессией, а число q – знаменателем геометрической прогрессии.
Таким образом, геометрическая прогрессия – это числовая последовательность {bn}, заданная рекуррентно соотношениями
b1 = b, bn = bn–1 q (n = 2, 3, 4…).
(b и q – заданные числа, b № 0, q № 0).
Пример 1. 2, 6, 18, 54, … – возрастающая геометрическая прогрессия b = 2,q = 3.
Пример 2. 2, –2, 2, –2, … – геометрическая прогрессия b = 2, q = –1.
Пример 3. 8, 8, 8, 8, … – геометрическая прогрессия b = 8, q = 1.
Геометрическая прогрессия является возрастающей последовательностью, если b1 > 0, q > 1, и убывающей, если b1 > 0, 0 < q < 1.
Одно из очевидных свойств геометрической прогрессии состоит в том, что если последовательность является геометрической прогрессией, то и последовательность квадратов, т.е.
b12, b22, b32, …, bn2,… является геометрической прогрессией, первый член которой равен b12, а знаменатель – q2.
Формула n-го члена геометрической прогрессии имеет вид
bn = b1qn–1.
Можно получить формулу суммы членов конечной геометрической прогрессии.
Пусть дана конечная геометрическая прогрессия
b1, b2, b3, …, bn
пусть Sn – сумма ее членов, т.е.
Sn= b1 + b2+ b3 + … + bn.
Принимается, что q № 1. Для определения Sn применяется искусственный прием: выполняются некоторые геометрические преобразования выражения Snq.
Тогда
Snq = (b1 + b2 + b3+ … + bn–1 + bn)q = b2 + b3 + b4 + …+ bn + bnq = Sn+ bnq– b1.
Таким образом, Snq = Sn + bnq – b1 и, следовательно,
![]() .
.
Это формула суммы n членов геометрической прогрессии для случая, когда q № 1.
При q = 1 формулу можно не выводить отдельно, очевидно, что в этом случае Sn = a1n.
Геометрической прогрессия названа потому, что в ней каждый член кроме первого, равен среднему геометрическому предыдущего и последующего членов. Действительно, так как
bn= bn-1q;
bn= bn+1/q,
следовательно, bn2= bn–1 bn+1 и верна следующая теорема(характеристическое свойство геометрической прогрессии):
числовая последовательность является геометрической прогрессией тогда и только тогда, когда квадрат каждого ее члена, кроме первого (и последнего в случае конечной последовательности), равен произведению предыдущего и последующего членов.
Предел последовательности.
Пусть есть
последовательность {cn} =
{1/n}. Эту последовательность
называют гармонической, поскольку
каждый ее член, начиная со второго, есть
среднее гармоническое между предыдущим
и последующим членами. Среднее
геометрическое чисел a и b есть
число ![]() ,
или
,
или ![]() .
С ростом n все члены геометрической
прогрессии убывают и их значение
приближается к нулю. В этом случае
принято говорить, что при n,
стремящемся к бесконечности, данная
последовательность сходитсяи нуль есть
ее предел. Записывается это так:
.
С ростом n все члены геометрической
прогрессии убывают и их значение
приближается к нулю. В этом случае
принято говорить, что при n,
стремящемся к бесконечности, данная
последовательность сходитсяи нуль есть
ее предел. Записывается это так:
![]() .
.
Строгое определение предела формулируется следующим образом:
Если существует такое число A, что для любого (сколь угодно малого) положительного числа e найдется такое натуральное N (вообще говоря, зависящее от e), что для всех n і N будет выполнено неравенство |an – A| < e, то говорят, что последовательность {an} сходится и A – ее предел.
Обозначается
это так: ![]() .
.
В противном случае последовательность называется расходящейся.
Опираясь на это определение, можно, например, доказать наличие предела A = 0 у гармонической последовательности {cn} = {1/n}. Пусть e – сколь угодно малое положительное число. Рассматривается разность
![]() .
.
Существует ли такое N, что для всех n і N выполняется неравенство 1/N <e? Если взять в качестве N любое натуральное число, превышающее 1/e, то для всех n і N выполняется неравенство 1/n Ј 1/N < e , что и требовалось доказать.
Доказать наличие предела у той или иной последовательности иногда бывает очень сложно. Наиболее часто встречающиеся последовательности хорошо изучены и приводятся в справочниках. Имеются важные теоремы, позволяющие сделать вывод о наличии предела у данной последовательности (и даже вычислить его), опираясь на уже изученные последовательности.
Теорема 1. Если последовательность имеет предел, то она ограничена.
Теорема 2. Если последовательность монотонна и ограничена, то она имеет предел.
Теорема 3. Если последовательность {an} имеет предел A, то последовательности {can}, {an + с} и {| an|} имеют пределы cA, A + c, |A| соответственно (здесь c – произвольное число).
Теорема 4. Если последовательности {an} и {bn} имеют пределы, равные Aи B соответственно, то последовательность {pan + qbn} имеет предел pA +qB.
Теорема 5. Если последовательности {an} и {bn}имеют пределы, равные A иB соответственно, то последовательность {anbn} имеет предел AB.
Теорема 6. Если последовательности {an} и {bn} имеют пределы, равные Aи B соответственно, и, кроме того, bn № 0 и B № 0, то последовательность {an / bn} имеет предел A/B.
Замеча́тельные преде́лы — термин, использующийся в советских и российских учебниках по математическому анализу для обозначения некоторых широко известных математических тождеств со взятием предела. Особенно известны:
-
Первый замечательный предел:
![]()
-
Второй замечательный предел:
![]()
Первый замечательный предел
![]()
Доказательство

Рассмотрим односторонние
пределы ![]() и
и ![]() и
докажем, что они равны 1.
и
докажем, что они равны 1.
Пусть ![]() .
Отложим этот угол на единичной окружности
(
.
Отложим этот угол на единичной окружности
(![]() ).
).
Точка K —
точка пересечения луча с окружностью,
а точка L — с касательной к
единичной окружности в точке ![]() .
Точка H — проекция точки K на
ось OX.
.
Точка H — проекция точки K на
ось OX.
Очевидно, что:
![]() (1)
(1)
(где ![]() —
площадь сектора
—
площадь сектора ![]() )
)
![]()
![]()
![]()
(из ![]() :
: ![]() )
)
Подставляя в (1), получим:
![]()
Так как
при ![]() :
:
![]()
Умножаем
на ![]() :
:
![]()
Перейдём к пределу:
![]()
![]()
![]()
Найдём левый односторонний предел:

Правый и левый односторонний пределы существуют и равны 1, а значит и сам предел равен 1.
Следствия
Доказательство следствий
![]()



Второй замечательный предел
![]() или
или ![]()
Доказательство второго замечательного предела:
Доказательство для натуральных значений x
![]() Докажем
вначале теорему для случая
последовательности
Докажем
вначале теорему для случая
последовательности ![]()
По
формуле бинома Ньютона: ![]()
Полагая ![]() ,
получим:
,
получим:
![]()
![]() (1)
(1)
Из данного
равенства (1) следует, что с увеличением
n число положительных слагаемых в правой
части увеличивается. Кроме того, при
увеличении n число ![]() убывает,
поэтому величины
убывает,
поэтому величины ![]() возрастают.
Поэтому последовательность
возрастают.
Поэтому последовательность ![]() — возрастающая,
при этом
— возрастающая,
при этом
![]() (2).
(2).
Покажем, что она ограничена. Заменим каждую скобку в правой части равенства на единицу, правая часть увеличится, получим неравенство
![]()
Усилим полученное неравенство, заменим 3,4,5, …, стоящие в знаменателях дробей, числом 2:
![]() .
.
Сумму в скобке найдём по формуле суммы членов геометрической прогрессии:
 .
.
Поэтому ![]() (3).
(3).
Итак,
последовательность ограничена сверху,
при этом ![]() выполняются
неравенства (2) и (3):
выполняются
неравенства (2) и (3): ![]() .
.
Следовательно,
на основании теоремы Вейерштрасса
(критерий сходимости последовательности)
последовательность ![]() монотонно
возрастает и ограниченна, значит имеет
предел, обозначаемый буквой e.
Т.е.
монотонно
возрастает и ограниченна, значит имеет
предел, обозначаемый буквой e.
Т.е. ![]()
![]()
![]() Зная, что второй замечательный предел
верен для натуральных значений x, докажем
второй замечательный предел для
вещественных x, то есть докажем, что
Зная, что второй замечательный предел
верен для натуральных значений x, докажем
второй замечательный предел для
вещественных x, то есть докажем, что ![]() .
Рассмотрим два случая:
.
Рассмотрим два случая:
1. Пусть ![]() .
Каждое значение x заключено между двумя
положительными целыми числами:
.
Каждое значение x заключено между двумя
положительными целыми числами: ![]() ,
где
,
где ![]() —
это целая часть x.
—
это целая часть x.
Отсюда
следует: ![]() ,
поэтому
,
поэтому
![]() .
.
Если ![]() ,
то
,
то ![]() .
Поэтому, согласно пределу
.
Поэтому, согласно пределу ![]() ,
имеем:
,
имеем:

![]() .
.
По признаку
(о пределе промежуточной функции)
существования пределов ![]() .
.
2. Пусть ![]() .
Сделаем подстановку
.
Сделаем подстановку ![]() ,
тогда
,
тогда
![]()
![]() .
.
Из двух
этих случаев вытекает, что ![]() для
вещественного x.
для
вещественного x. ![]()
Следствия
-

-

-

-

-
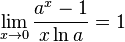 для
для  ,
, 
-

Доказательства следствий

Теорема Вейерштрасса об ограниченной возрастающей последовательности утверждает, что любая ограниченная возрастающая последовательность имеет предел, причем этот предел равен ее точной верхней грани. Несмотря на прозрачность и очевидность доказательства, эта теорема оказывается очень удобной для нахождения пределов многих последовательностей, или хотя бы доказательства их существования.
Доказательство и формулировка
Пусть ![]() -
возрастающая последовательность,
ограниченная собственным супремумом
-
возрастающая последовательность,
ограниченная собственным супремумом ![]() .
Тогда
.
Тогда ![]() .
Действительно, с одной стороны, если
найдется такое число
.
Действительно, с одной стороны, если
найдется такое число ![]() ,
что в
,
что в ![]() нет
элементов
нет
элементов ![]() ,
то (
,
то (![]() )
- число, меньшее
)
- число, меньшее ![]() ,
но большее любого элемента
,
но большее любого элемента ![]() .
Cледовательно
.
Cледовательно ![]() -
не супремум, пришли к противоречию.
Значит,
-
не супремум, пришли к противоречию.
Значит, ![]() - предельная
точка
- предельная
точка ![]() .
Но у возрастающей последовательности
может быть лишь одна предельная точка,
это ее предел. Теорема доказана.
.
Но у возрастающей последовательности
может быть лишь одна предельная точка,
это ее предел. Теорема доказана.
Точки разрыва и их классификация.
Рассмотрим некоторую функцию f(x), непрерывную в окрестности точки х0, за исключением может быть самой этой точки. Из определения точки разрыва функции следует, что х = х0 является точкой разрыва, если функция не определена в этой точке, или не является в ней непрерывной.
Следует отметить также, что непрерывность функции может быть односторонней. Поясним это следующим образом.
Если
односторонний предел (см. выше) ![]() ,
то функция называется непрерывной
справа.
,
то функция называется непрерывной
справа.
|
|
|
|
|
|
х0
Если
односторонний предел (см. выше) ![]() ,
то функция называется непрерывной
слева.
,
то функция называется непрерывной
слева.
|
|
|
|
|
|
х0
Определение. Точка х0 называется точкой разрыва функции f(x), если f(x) не определена в точке х0 или не является непрерывной в этой точке.
Определение. Точка х0 называется точкой разрыва 1- го рода, если в этой точке функция f(x) имеет конечные, но не равные друг другу левый и правый пределы.
![]()
Для выполнения условий этого определения не требуется, чтобы функция была определена в точке х = х0, достаточно того, что она определена слева и справа от нее.
Из определения можно сделать вывод, что в точке разрыва 1 – го рода функция может иметь только конечный скачок. В некоторых частных случаях точку разрыва 1 – го рода еще иногда называют устранимой точкой разрыва, но подробнее об этом поговорим ниже.
Определение. Точка х0 называется точкой разрыва 2 – го рода, если в этой точке функция f(x) не имеет хотя бы одного из односторонних пределов или хотя бы один из них бесконечен.
Пример. Функция Дирихле (Дирихле Петер Густав(1805-1859) – немецкий математик, член- корреспондент Петербургской АН 1837г)
![]()
не является непрерывной в любой точке х0.
Пример. Функция f(x)
= ![]() имеет
в точке х0 =
0 точку разрыва 2 – го рода, т.к.
имеет
в точке х0 =
0 точку разрыва 2 – го рода, т.к.
![]() .
.
![]()

Пример. f(x)
= ![]()
Функция
не определена в точке х = 0, но имеет в
ней конечный предел ![]() ,
т.е. в точке х = 0 функция имеет точку
разрыва 1 – го рода. Это – устранимая
точка разрыва, т.к. если доопределить
функцию:
,
т.е. в точке х = 0 функция имеет точку
разрыва 1 – го рода. Это – устранимая
точка разрыва, т.к. если доопределить
функцию:

График этой функции:

Пример. f(x)
= ![]() =
=![]()
Пример. f(x)
= ![]() =
=![]()
 y
y
1
0 x
-1
Эта функция также обозначается sign(x) – знак х. В точке х = 0 функция не определена. Т.к. левый и правый пределы функции различны, то точка разрыва – 1 – го рода. Если доопределить функцию в точке х = 0, положив f(0) = 1, то функция будет непрерывна справа, если положить f(0) = -1, то функция будет непрерывной слева, если положить f(x) равное какому- либо числу, отличному от 1 или –1, то функция не будет непрерывна ни слева, ни справа, но во всех случаях тем не менее будет иметь в точке х = 0 разрыв 1 – го рода. В этом примере точка разрыва 1 – го рода не является устранимой.
Таким образом, для того, чтобы точка разрыва 1 – го рода была устранимой, необходимо, чтобы односторонние пределы справа и слева были конечны и равны, а функция была бы в этой точке не определена.
Определение точек разрыва
Дадим теперь определение точек разрыва функции.
Определение 3.2
Точка ![]() называется точкой
разрыва функции
называется точкой
разрыва функции ![]() ,
если она определена в некоторой проколотой
окрестности точки
,
если она определена в некоторой проколотой
окрестности точки ![]() (то
есть определена на некотором интервале,
для которого
(то
есть определена на некотором интервале,
для которого ![]() служит
внутренней точкой, но в самой точке
служит
внутренней точкой, но в самой точке ![]() ,
возможно, не определена) и выполняется
хотя бы одно из следующих условий:
,
возможно, не определена) и выполняется
хотя бы одно из следующих условий:
1) не
существует предела слева ![]() ;
;
2) не
существует предела справа ![]() ;
;
3) пределы
слева ![]() и
справа
и
справа ![]() существуют,
но не равны друг другу:
существуют,
но не равны друг другу: ![]() ;
;
4) пределы
слева ![]() и
справа
и
справа ![]() существуют
и равны друг другу:
существуют
и равны друг другу: ![]() ,
но не совпадают со значением функции в
точке
,
но не совпадают со значением функции в
точке ![]() :
: ![]() ,
или функция
,
или функция ![]() не
определена в точке
не
определена в точке ![]() .
.
Если имеет
место либо случай 3, либо случай 4, то
точка разрыва ![]() называется точкой
разрыва первого рода, а поведение
функции в окрестности точки
называется точкой
разрыва первого рода, а поведение
функции в окрестности точки ![]() называетсяразрывом
первого рода в точке
называетсяразрывом
первого рода в точке ![]() ;
в случае 4 точка разрыва первого рода
называется устранимой точкой
разрыва, а разрыв функции в этой
точке -- устранимым разрывом.
;
в случае 4 точка разрыва первого рода
называется устранимой точкой
разрыва, а разрыв функции в этой
точке -- устранимым разрывом.
Если же
имеет место либо случай 1, либо случай
2 (либо и тот и другой сразу), то точка
разрыва ![]() называется точкой
разрыва второго рода, а поведение
функции в окрестности этой точки -- разрывом
второго рода в точке
называется точкой
разрыва второго рода, а поведение
функции в окрестности этой точки -- разрывом
второго рода в точке ![]() .
.
Итак, если
функция ![]() имеет
разрыв первого рода в точке
имеет
разрыв первого рода в точке ![]() ,
то существуют, как часто говорят, значения
функции "на берегах разрыва":
,
то существуют, как часто говорят, значения
функции "на берегах разрыва": ![]() и
и ![]() ,
но точка
,
но точка ![]() не
является точкой непрерывности.
не
является точкой непрерывности.

Рис.3.2.![]() --
точка разрыва первого рода
--
точка разрыва первого рода
Если значения
на берегах разрыва разные, то значение
функции в точке ![]() может
быть любым (или вообще отсутствовать),
всё равно
может
быть любым (или вообще отсутствовать),
всё равно ![]() будет
давать разрыв первого рода. Если же
значения на берегах разрыва совпадают,
то для наличия разрыва нужно, чтобы либо
эти совпадающие значения были отличны
от значения функции в точке
будет
давать разрыв первого рода. Если же
значения на берегах разрыва совпадают,
то для наличия разрыва нужно, чтобы либо
эти совпадающие значения были отличны
от значения функции в точке ![]() ,
либо функция в этой точке была вовсе не
определена. Если в этом случае
переопределить (или доопределить)
функцию
,
либо функция в этой точке была вовсе не
определена. Если в этом случае
переопределить (или доопределить)
функцию ![]() в
точке
в
точке ![]() ,
положив
,
положив ![]() ,
то полученная изменённая функция будет
уже непрерывна в точке
,
то полученная изменённая функция будет
уже непрерывна в точке ![]() и
разрыв в точке
и
разрыв в точке ![]() исчезнет;
отсюда и название такого разрыва --
устранимый.
исчезнет;
отсюда и название такого разрыва --
устранимый.

Рис.3.3.![]() --
точка устранимого разрыва
--
точка устранимого разрыва
Наконец, к
разрывам второго рода, как видно из
определения, относятся все разрывы,
которые не принадлежат к разрывам
первого рода; некоторые из возможных
способов поведения функции в окрестности
точки ![]() ,
где происходит разрыв второго рода,
представлены на следующем рисунке.
,
где происходит разрыв второго рода,
представлены на следующем рисунке.



Рис.3.4.![]() --
точка разрыва второго рода. Некоторые
возможные варианты
--
точка разрыва второго рода. Некоторые
возможные варианты
Пример 3.3
Рассмотрим функцию  ,
для которой
,
для которой
![]()
Функция
имеет разрывы при ![]() и
при
и
при ![]() .
Нетрудно видеть, что при
.
Нетрудно видеть, что при ![]()
 В
точках
В
точках ![]() и
и ![]() функция
имеет неустранимые разрывы первого
рода. В точке
функция
имеет неустранимые разрывы первого
рода. В точке ![]() имеем:
имеем:
![]()
(значения
на краях разыва существуют, но не
совпадают); в точке ![]() --
--
![]()
(снова пределы слева и справа существуют, но не совпадают).

Рис.3.5.График
функции ![]()
Пример 3.4
Функция  имеет
при
имеет
при ![]() разрыв
второго рода, так как
разрыв
второго рода, так как ![]() при
при ![]() и
и ![]() при
при ![]() .
.

Рис.3.6.График
функции ![]()
Пример 3.5
Функция  имеет
при
имеет
при ![]() разрыв
второго рода, так как
разрыв
второго рода, так как ![]() при
при ![]() и
при
и
при ![]() .
.

Рис.3.7.График
функции ![]()
Пример 3.6
Возьмём ![]() .
Все точки области определения
.
Все точки области определения ![]() этой
элементарной функции являются точками
непрерывности. Поскольку
этой
элементарной функции являются точками
непрерывности. Поскольку ![]() не
входит в область определения функции
не
входит в область определения функции ![]() ,
но
,
но ![]() определена
во всех точках любой проколотой
окрестности 0, то 0 -- точка разрыва
функции
определена
во всех точках любой проколотой
окрестности 0, то 0 -- точка разрыва
функции ![]() .
Разобранный вышепример
3.2 показывает, что если доопределить
эту функцию при
.
Разобранный вышепример
3.2 показывает, что если доопределить
эту функцию при ![]() ,
положив
,
положив ![]() ,
то функция становится непрерывной в
точке 0. Значит, 0 -- точка разрыва
первого рода для функции
,
то функция становится непрерывной в
точке 0. Значит, 0 -- точка разрыва
первого рода для функции ![]() .
.

Рис.3.8.Устранимый
разрыв функции ![]()
Пример 3.7
Рассмотрим функцию ![]() .
Её область определения
.
Её область определения ![]() состоит
из точек непрерывности, так как это
элементарная функция. Точка
состоит
из точек непрерывности, так как это
элементарная функция. Точка ![]() ,
в которой функция не определена, --
это точка разрыва функции. Поскольку
,
в которой функция не определена, --
это точка разрыва функции. Поскольку  при
при ![]() ,
то
,
то ![]() .
Это означает, что при
.
Это означает, что при ![]() функция
имеет устранимый разрыв и становится
непрерывной на всей вещественной оси,
если положить
функция
имеет устранимый разрыв и становится
непрерывной на всей вещественной оси,
если положить ![]() .
.

Рис.3.9.Устранимый
разрыв функции ![]()
Пример 3.8
Рассмотрим функцию ![]() ,
где
,
где ![]() .
При
.
При ![]() она
имеет разрыв, так как
она
имеет разрыв, так как ![]() .
Поскольку
.
Поскольку ![]() --
ограниченная функция, а
--
ограниченная функция, а ![]() при
при ![]() ,
то
,
то ![]() (по теореме
2.7). Следовательно, разрыв устранимый,
и если доопределить функцию, положив
(по теореме
2.7). Следовательно, разрыв устранимый,
и если доопределить функцию, положив ![]() ,
она становится непрерывной при всех
,
она становится непрерывной при всех ![]() .
.

Рис.3.10.График
функции ![]() при
при ![]()
Пример 3.9
Рассмотрим функцию ![]() ,
заданную равенством
,
заданную равенством
![]()
При ![]() ,
, ![]() ,
, ![]() ,
так что последовательность
,
так что последовательность ![]() --
это геометрическая прогрессия со
знаменателем
--
это геометрическая прогрессия со
знаменателем ![]() ,
, ![]() ,
и
,
и ![]() При
При ![]() ,
, ![]() ,
, ![]() ,
и все
,
и все ![]() ,
так что
,
так что ![]() При
При ![]() ,
, ![]() ,
, ![]() ,
и последовательность имеет вид
,
и последовательность имеет вид
![]()
Эта
последовательность предела не имеет,
так что функция ![]() не
определена при
не
определена при ![]() ,
, ![]() .
.
Рис.3.11.График
функции ![]()
Получаем,
что ![]() .
Точками разрыва этой функции служат
как все точки, не принадлежащие области
определения (точки вида
.
Точками разрыва этой функции служат
как все точки, не принадлежащие области
определения (точки вида ![]() ,
, ![]() ),
так и все точки вида
),
так и все точки вида ![]() ,
, ![]() ,
в которых функция принимает значение 1.
Все точки разрыва -- устранимые, так
как пределы функции слева и справа в
этих точках совпадают и равны 0.
,
в которых функция принимает значение 1.
Все точки разрыва -- устранимые, так
как пределы функции слева и справа в
этих точках совпадают и равны 0.
Пример 3.10
Рассмотрим функцию ![]() ;
её область определения
;
её область определения ![]() ,
и точка
,
и точка ![]() --
точка разрыва. Рассмотрим поведение
функции слева и справа от точки разрыва.
При
--
точка разрыва. Рассмотрим поведение
функции слева и справа от точки разрыва.
При ![]() будет
будет ![]() и
и ![]() ;
при
;
при ![]() будет
будет ![]() и
и ![]() .
Итак, значения "на правом берегу"
разрыва не существует, и разрыв функции
.
Итак, значения "на правом берегу"
разрыва не существует, и разрыв функции ![]() в
точке
в
точке ![]() --
второго рода.
--
второго рода.

Рис.3.12.График
функции ![]()
Замечание 3.1
Если функция ![]() не
определена на интервале, примыкающем
к точке
не
определена на интервале, примыкающем
к точке ![]() слева
или справа, то точку
слева
или справа, то точку ![]() мы
не считаем точкой разрыва функции.
мы
не считаем точкой разрыва функции.
Пример 3.11
Рассмотрим функцию  .
Её область определения --
.
Её область определения -- ![]() .
При
.
При ![]() и
при
и
при ![]() знаменатель
знаменатель ![]() стремится
к 0 и положителен, так что
стремится
к 0 и положителен, так что ![]() .
однако точки
.
однако точки ![]() и
и ![]() мы
не считаем точками разрыва, так как
функция
мы
не считаем точками разрыва, так как
функция ![]() не
определена при
не
определена при ![]() и
при
и
при ![]() .
.

Рис.3.13.График
функции 
Пример 3.12
Рассмотрим функцию  .
Её область определения -- это
.
Её область определения -- это ![]() .
Точка
.
Точка ![]() не
является точкой разрыва функции
не
является точкой разрыва функции ![]() ,
несмотря на характер её поведения при
,
несмотря на характер её поведения при ![]() ,
поскольку функция
,
поскольку функция ![]() не
определена при
не
определена при ![]() .
.

Рис.3.14.График
функции 
Приближенные вычисления с помощью дифференциала
На данном уроке мы рассмотрим широко распространенную задачу о приближенном вычислении значения функции с помощью дифференциала. Здесь и далее речь пойдёт о дифференциалах первого порядка, для краткости я часто буду говорить просто «дифференциал». Задача о приближенных вычислениях с помощью дифференциала обладает жёстким алгоритмом решения, и, следовательно, особых трудностей возникнуть не должно. Единственное, есть небольшие подводные камни, которые тоже будут подчищены. Так что смело ныряйте головой вниз.
Кроме того, на странице присутствуют формулы нахождения абсолютной и относительной погрешность вычислений. Материал очень полезный, поскольку погрешности приходится рассчитывать и в других задачах. Физики, где ваши аплодисменты? =)
Для успешного освоения примеров необходимо уметь находить производные функций хотя бы на среднем уровне, поэтому если с дифференцированием совсем нелады, пожалуйста, начните с урока Как найти производную?Также рекомендую прочитать статьюПростейшие задачи с производной, а именно параграфы о нахождении производной в точке и нахождении дифференциала в точке. Из технических средств потребуется микрокалькулятор с различными математическими функциями. Можно использовать Эксель, но в данном случае он менее удобен.
Урок состоит из двух частей:
– Приближенные вычисления с помощью дифференциала функции одной переменной.
– Приближенные вычисления с помощью полного дифференциала функции двух переменных.
Кому что нужно. На самом деле можно было разделить богатство на две кучи, по той причине, что второй пункт относится к приложениям функции нескольких переменных. Но что поделать, вот люблю я длинные статьи.
Рассматриваемое задание тесно связано с понятием дифференциала, и его геометрический смысл можно узнать на уроке Что такое производня? А сейчас ограничимся формальным рассмотрением примеров, чего вполне достаточно, чтобы научиться их решать.
Приближенные вычисления с помощью дифференциала функции одной переменной
В первом
параграфе рулит функция одной переменной.
Как все знают, она обозначается через ![]() или
через
или
через ![]() .
Для данной задачи намного удобнее
использовать второе обозначение. Сразу
перейдем к популярному примеру, который
часто встречается на практике:
.
Для данной задачи намного удобнее
использовать второе обозначение. Сразу
перейдем к популярному примеру, который
часто встречается на практике:
Пример 1
Вычислить
приближенно ![]() ,
заменяя приращения функции ее
дифференциалом.
,
заменяя приращения функции ее
дифференциалом.
Решение: Пожалуйста, перепишите в тетрадь рабочую формулу для приближенного вычисления с помощью дифференциала:
![]()
Начинаем разбираться, здесь всё просто!
На первом
этапе необходимо составить функцию ![]() .
По условию предложено вычислить
кубический корень из числа:
.
По условию предложено вычислить
кубический корень из числа: ![]() ,
поэтому соответствующая функция имеет
вид:
,
поэтому соответствующая функция имеет
вид: ![]() .
Нам нужно с помощью формулы найти
приближенное значение
.
Нам нужно с помощью формулы найти
приближенное значение ![]() .
.
Смотрим
на левую часть формулы ![]() ,
и в голову приходит мысль, что число 67
необходимо представить в виде
,
и в голову приходит мысль, что число 67
необходимо представить в виде ![]() .
Как проще всего это сделать? Рекомендую
следующий алгоритм: вычислим данное
значение на калькуляторе:
.
Как проще всего это сделать? Рекомендую
следующий алгоритм: вычислим данное
значение на калькуляторе:
![]() –
получилось 4 с хвостиком, это важный
ориентир для решения.
–
получилось 4 с хвостиком, это важный
ориентир для решения.
В
качестве ![]() подбираем
«хорошее» значение, чтобы корень
извлекался нацело. Естественно, это
значение
подбираем
«хорошее» значение, чтобы корень
извлекался нацело. Естественно, это
значение ![]() должно
быть как можно ближе к 67. В
данном случае:
должно
быть как можно ближе к 67. В
данном случае: ![]() .
Действительно:
.
Действительно: ![]() .
.
Примечание:
Когда с подбором ![]() всё
равно возникает затруднение, просто
посмотрите на скалькулированное значение
(в данном случае
всё
равно возникает затруднение, просто
посмотрите на скалькулированное значение
(в данном случае ![]() ),
возьмите ближайшую целую часть (в
данном случае 4) и возведите её нужную
в степень (в данном случае
),
возьмите ближайшую целую часть (в
данном случае 4) и возведите её нужную
в степень (в данном случае ![]() ).
В результате и будет выполнен нужный
подбор:
).
В результате и будет выполнен нужный
подбор: ![]() .
.
Если ![]() ,
то приращение аргумента:
,
то приращение аргумента: ![]() .
.
Итак, число
67 представлено в виде суммы ![]()
Далее
работаем с правой частью формулы ![]() .
.
Сначала
вычислим значение функции в точке ![]() .
Собственно, это уже сделано ранее:
.
Собственно, это уже сделано ранее:
![]()
Дифференциал
в точке находится по формуле:
![]() –
тоже можете переписать к себе в тетрадь.
–
тоже можете переписать к себе в тетрадь.
Из формулы
следует, что нужно взять первую
производную:
![]()
И найти её
значение в точке ![]() :
:
![]()
Таким
образом:
![]()
Всё готово!
Согласно формуле ![]() :
:
![]()
Найденное
приближенное значение достаточно близко
к значению ![]() ,
вычисленному с помощью микрокалькулятора.
,
вычисленному с помощью микрокалькулятора.
Ответ: ![]()
Пример 2
Вычислить
приближенно ![]() ,
заменяя приращения функции ее
дифференциалом.
,
заменяя приращения функции ее
дифференциалом.
Это пример
для самостоятельного решения. Примерный
образец чистового оформления и ответ
в конце урока. Начинающим сначала
рекомендую вычислить точное значение ![]() на
микрокалькуляторе, чтобы выяснить,
какое число принять за
на
микрокалькуляторе, чтобы выяснить,
какое число принять за ![]() ,
а какое – за
,
а какое – за ![]() .
Следует отметить, что
.
Следует отметить, что ![]() в
данном примере будет отрицательным.
в
данном примере будет отрицательным.
У некоторых, возможно, возник вопрос, зачем нужна эта задача, если можно всё спокойно и более точно подсчитать на калькуляторе? Согласен, задача глупая и наивная. Но попытаюсь немного её оправдать. Во-первых, задание иллюстрирует смысл дифференциала функции. Во-вторых, в древние времена, калькулятор был чем-то вроде личного вертолета в наше время. Сам видел, как из местного политехнического института году где-то в 1985-86 выбросили компьютер размером с комнату (со всего города сбежались радиолюбители с отвертками, и через пару часов от агрегата остался только корпус). Антиквариат водился и у нас на физмате, правда, размером поменьше – где-то с парту. Вот так вот и мучились наши предки с методами приближенных вычислений. Конная повозка – тоже транспорт.
Так или иначе, задача осталась в стандартном курсе высшей математики, и решать её придётся. Это основной ответ на ваш вопрос =)
Пример 3
Вычислить
приближенно с помощью дифференциала
значение функции ![]() в
точке
в
точке ![]() .
Вычислить более точное значение функции
в точке
.
Вычислить более точное значение функции
в точке ![]() с
помощью микрокалькулятора, оценить
абсолютную и относительную погрешность
вычислений.
с
помощью микрокалькулятора, оценить
абсолютную и относительную погрешность
вычислений.
Фактически
то же самое задание, его запросто можно
переформулировать так: «Вычислить
приближенное значение ![]() с
помощью дифференциала»
с
помощью дифференциала»
Решение: Используем
знакомую формулу: ![]() В
данном случае уже дана готовая функция:
В
данном случае уже дана готовая функция: ![]() .
Ещё раз обращаю внимание, что для
обозначения функции вместо «игрека»
удобнее использовать
.
Ещё раз обращаю внимание, что для
обозначения функции вместо «игрека»
удобнее использовать ![]() .
.
Значение ![]() необходимо
представить в виде
необходимо
представить в виде ![]() .
Ну, тут легче, мы видим, что число 1,97
очень близко к «двойке», поэтому
напрашивается
.
Ну, тут легче, мы видим, что число 1,97
очень близко к «двойке», поэтому
напрашивается ![]() .
И, следовательно:
.
И, следовательно: ![]() .
Вычислим
значение функции в точке
.
Вычислим
значение функции в точке ![]() :
:
![]()
Используя
формулу ![]() ,
вычислим дифференциал в этой же точке.
,
вычислим дифференциал в этой же точке.
Находим
первую производную:
![]()
И её значение
в точке ![]() :
:
![]()
Таким
образом, дифференциал в точке:
![]()
В результате,
по формуле ![]() :
:
![]()
Вторая часть задания состоит в том, чтобы найти абсолютную и относительную погрешность вычислений.
Абсолютная и относительная погрешность вычислений
Абсолютная
погрешность вычислений находится
по формуле:
![]()
Знак модуля показывает, что нам без разницы, какое значение больше, а какое меньше. Важно, насколько далеко приближенный результат отклонился от точного значения в ту или иную сторону.
Относительная
погрешность вычислений находится
по формуле:
![]() ,
или, то же самое:
,
или, то же самое:
![]()
Относительная погрешность показывает, на сколько процентов приближенный результат отклонился от точного значения. Существует версия формулы и без домножения на 100%, но на практике я почти всегда вижу вышеприведенный вариант с процентами.
После
короткой справки вернемся к нашей
задаче, в которой мы вычислили приближенное
значение функции ![]() с
помощью дифференциала.
с
помощью дифференциала.
Вычислим
точное значение функции с помощью
микрокалькулятора:
![]() ,
строго говоря, значение всё равно
приближенное, но мы будем считать его
точным. Такие уж задачи встречаются.
,
строго говоря, значение всё равно
приближенное, но мы будем считать его
точным. Такие уж задачи встречаются.
Вычислим
абсолютную погрешность:
![]()
Вычислим
относительную погрешность:
![]() ,
получены тысячные доли процента, таким
образом, дифференциал обеспечил просто
отличное приближение.
,
получены тысячные доли процента, таким
образом, дифференциал обеспечил просто
отличное приближение.
Ответ: ![]() ,
абсолютная погрешность вычислений
,
абсолютная погрешность вычислений ![]() ,
относительная погрешность вычислений
,
относительная погрешность вычислений ![]()
Следующий пример для самостоятельного решения:
Пример 4
Вычислить
приближенно с помощью дифференциала
значение функции ![]() в
точке
в
точке ![]() .
Вычислить более точное значение функции
в данной точке, оценить абсолютную и
относительную погрешность вычислений.
.
Вычислить более точное значение функции
в данной точке, оценить абсолютную и
относительную погрешность вычислений.
Примерный образец чистового оформления и ответ в конце урока.
Многие обратили внимание, что во всех рассмотренных примерах фигурируют корни. Это не случайно, в большинстве случаев в рассматриваемой задаче действительно предлагаются функции с корнями.
Но для страждущих читателей я раскопал небольшой пример с арксинусом:
Пример 5
Вычислить
приближенно с помощью дифференциала
значение функции ![]() в
точке
в
точке ![]()
Этот коротенький, но познавательный пример тоже для самостоятельного решения. А я немного отдохнул, чтобы с новыми силами рассмотреть особое задание:
Пример 6
Вычислить
приближенно с помощью дифференциала ![]() ,
результат округлить до двух знаков
после запятой.
,
результат округлить до двух знаков
после запятой.
Решение: Что
нового в задании? По условию требуется
округлить результат до двух знаков
после запятой. Но дело не в этом, школьная
задача округления, думаю, не представляет
для вас сложностей. Дело в том, что у нас
дан тангенс с аргументом, который
выражен в градусах. Что делать, когда
вам предлагается для решения
тригонометрическая функция с градусами?
Например, ![]() и
т. д.
Алгоритм решения принципиально
сохраняется, то есть необходимо, как и
в предыдущих примерах, применить
формулу
и
т. д.
Алгоритм решения принципиально
сохраняется, то есть необходимо, как и
в предыдущих примерах, применить
формулу ![]()
Записываем
очевидную функцию ![]()
Значение ![]() нужно
представить в виде
нужно
представить в виде ![]() .
Серьёзную помощь окажет таблица
значений тригонометрических функций.
Кстати, кто её не распечатал, рекомендую
это сделать, поскольку заглядывать туда
придется на протяжении всего курса
изучения высшей математики.
.
Серьёзную помощь окажет таблица
значений тригонометрических функций.
Кстати, кто её не распечатал, рекомендую
это сделать, поскольку заглядывать туда
придется на протяжении всего курса
изучения высшей математики.
Анализируя
таблицу, замечаем «хорошее» значение
тангенса, которое близко располагается
к 47 градусам: ![]()
Таким
образом: ![]()
После предварительного анализа градусы необходимо перевести в радианы. Так, и только так!
В данном
примере непосредственно из тригонометрической
таблицы можно выяснить, что ![]() .
По формуле перевода градусов в
радианы:
.
По формуле перевода градусов в
радианы: ![]() (формулы
можно найти в той же таблице).
(формулы
можно найти в той же таблице).
Дальнейшее
шаблонно:

Таким
образом: ![]() (при
вычислениях используем значение
(при
вычислениях используем значение ![]() ).
Результат, как и требовалось по условию,
округлён до двух знаков после запятой.
).
Результат, как и требовалось по условию,
округлён до двух знаков после запятой.
Ответ: ![]()
Пример 7
Вычислить
приближенно с помощью дифференциала ![]() ,
результат округлить до трёх знаков
после запятой.
,
результат округлить до трёх знаков
после запятой.
Это пример для самостоятельного решения. Полное решение и ответ в конце урока.
Как видите, ничего сложного, градусы переводим в радианы и придерживаемся обычного алгоритма решения.
|
Свойства дифференциала |
||
|
|
||
|

Производные простых функций
Вывод
![]()
-
 когда
когда  и
и  определены,
определены, 
Вывод
![]()
![]()



![]()
![]()
![]()
Вывод
Так как ![]() ,
то пусть
,
то пусть ![]() и
и ![]()
Тогда ![]()
Производные экспоненциальных и логарифмических функций
Вывод
![]()
Вывод
![]()
![]()
![]()
![]()
Производные тригонометрических и обратных тригонометрических функций
Вывод
![]()
![]()
![]()
![]()
![]()
![]()
Производные гиперболических функций
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
при
,
при ![]()
![]()
![]() ,
при
,
при ![]()
![]()
Правила дифференцирования общих функций
![]()
![]()
![]()
![]() (частный
случай формулы Лейбница)
(частный
случай формулы Лейбница)


![]() — Правило
дифференцирования сложной функции
— Правило
дифференцирования сложной функции
![]()
![]()
Производная обратной функции
Пусть ![]() -
функция от аргумента x в некотором
интервале
-
функция от аргумента x в некотором
интервале ![]() .
Если в уравнении
.
Если в уравнении ![]() y
считать аргументом, а x - функцией, то
возникает новая функция
y
считать аргументом, а x - функцией, то
возникает новая функция ![]() ,
где
,
где ![]() - функция
обратная данной.
- функция
обратная данной.
Содержание
-
1 Теорема (о дифференцировании обратной функции)
-
2 Примеры
-
3 См. также
-
4 Примечания
-
5 Литература
Теорема (о дифференцировании обратной функции)[править | править исходный текст]
Для дифференцируемой функции с производной, отличной от нуля, производная обратной функции равна обратной величине производной данной функции, т.е
![]()
Доказательство
Пусть ![]() -
дифференцируемая функция,
-
дифференцируемая функция, ![]() .
Пусть
.
Пусть ![]() -
приращение независимой переменной y
и
-
приращение независимой переменной y
и ![]() -
соответствующее приращение обратной
функции
-
соответствующее приращение обратной
функции ![]() .
Напишем
тождество
.
Напишем
тождество
![]()
Переходя
в этом равенстве к пределу при ![]() ,
которое влечет за собой стремление
,
которое влечет за собой стремление ![]() к
нулю (
к
нулю (![]() ),
получим:
),
получим:
![]() ,
где
,
где ![]() -
производная обратной функции.
-
производная обратной функции.
Замечание Если пользоваться обозначениями Лейбница, то выше доказанная формула примет вид

Примеры![]() ,
,

-
 ,
,
![]()
![]() .
.
Таблица интегралов
Применяя таблицу производных и правила взятия интегралов, можно составить такую таблицу интегралов:
1). 
2). ∫cosx dx=sinx+c
3). ∫sinx dx=-cosx+c
4). 
5). 
6). 
7). 
8). 
9). 
10). 
11). 
12). 
13). 
14). 
Производная функции, заданной неявно
Или короче – производная неявной функции. Что такое неявная функция? Поскольку мои уроки носят практическую направленность, я стараюсь избегать определений, формулировок теорем, но здесь это будет уместно сделать. А что такое вообще функция?
Функция
одной переменной ![]() – это
правило, по которому каждому значению
независимой переменной
– это
правило, по которому каждому значению
независимой переменной ![]() соответствует
одно и только одно значение функции
соответствует
одно и только одно значение функции ![]() .
.
Переменная ![]() называется независимой
переменной или аргументом.
Переменная
называется независимой
переменной или аргументом.
Переменная ![]() называется зависимой
переменной или функцией.
называется зависимой
переменной или функцией.
Грубо говоря, буковка «игрек» в данном случае – и есть функция.
До сих пор мы рассматривали функции, заданные в явном виде. Что это значит? Устроим разбор полётов на конкретных примерах.
Рассмотрим
функцию ![]()
Мы видим,
что слева у нас одинокий «игрек»
(функция), а справа – только «иксы».
То есть, функция ![]() в
явном виде выражена через независимую
переменную
в
явном виде выражена через независимую
переменную ![]() .
.
Рассмотрим
другую функцию: ![]()
Здесь
переменные ![]() и
и ![]() расположены
«вперемешку». Причем никакими
способами невозможно выразить
«игрек» только через «икс». Что это за
способы? Перенос слагаемых из части в
часть со сменой знака, вынесение за
скобки, перекидывание множителей по
правилу пропорции и др. Перепишите
равенство
расположены
«вперемешку». Причем никакими
способами невозможно выразить
«игрек» только через «икс». Что это за
способы? Перенос слагаемых из части в
часть со сменой знака, вынесение за
скобки, перекидывание множителей по
правилу пропорции и др. Перепишите
равенство ![]() и
попробуйте выразить «игрек» в явном
виде:
и
попробуйте выразить «игрек» в явном
виде: ![]() .
Можно крутить-вертеть уравнение часами,
но у вас этого не получится.
.
Можно крутить-вертеть уравнение часами,
но у вас этого не получится.
Разрешите
познакомить: ![]() –
пример неявной функции.
–
пример неявной функции.
В курсе математического анализа доказано, что неявная функция существует (однако не всегда), у неё есть график (точно так же, как и у «нормальной» функции). У неявной функции точно так же существует первая производная, вторая производная и т.д. Как говорится, все права секс-меньшинств соблюдены.
И на этом уроке мы научимся находить производную от функции, заданной неявно. Это не так сложно! Все правила дифференцирования, таблица производных элементарных функций остаются в силе. Разница в одном своеобразном моменте, который мы рассмотрим прямо сейчас.
Да, и сообщу хорошую новость – рассмотренные ниже задания выполняются по довольно жесткому и чёткому алгоритму без камня перед тремя дорожками.
Пример 1
Найти
производную от функции, заданной неявно ![]()
1) На первом
этапе навешиваем штрихи на обе части:
![]()
2) Используем
правила линейности производной (первые
два правила урока ):
![]()
3)
Непосредственное дифференцирование.
Как
дифференцировать ![]() и
и ![]() совершенно
понятно. Что делать там, где под штрихами
есть «игреки»?
совершенно
понятно. Что делать там, где под штрихами
есть «игреки»?
![]() –
просто до безобразия, производная
от функции равна её производной:
–
просто до безобразия, производная
от функции равна её производной: ![]() .
.
Как
дифференцировать ![]() Здесь
у нас сложная функция. Почему?
Вроде бы под синусом всего одна буква
«игрек». Но, дело в том, что всего одна
буква «игрек» – САМА ПО СЕБЕ ЯВЛЯЕТСЯ
ФУНКЦИЕЙ(см. определение в начале
урока). Таким образом, синус – внешняя
функция,
Здесь
у нас сложная функция. Почему?
Вроде бы под синусом всего одна буква
«игрек». Но, дело в том, что всего одна
буква «игрек» – САМА ПО СЕБЕ ЯВЛЯЕТСЯ
ФУНКЦИЕЙ(см. определение в начале
урока). Таким образом, синус – внешняя
функция, ![]() –
внутренняя функция. Используем правило
дифференцирования сложной функции
–
внутренняя функция. Используем правило
дифференцирования сложной функции ![]() :
:
![]()
Произведение
дифференцируем по обычному правилу ![]() :
:
![]()
Обратите
внимание, что ![]() –
тоже сложная функция, любой «игрек
с наворотами» – сложная функция:
–
тоже сложная функция, любой «игрек
с наворотами» – сложная функция:
![]()
Само
оформление решения должно выглядеть
примерно так:
![]()
![]() Если
есть скобки, то раскрываем их:
Если
есть скобки, то раскрываем их:
![]()
4) В левой
части собираем слагаемые, в которых
есть «игрек» со штрихом. В правую часть
– переносим всё остальное:
![]()
5) В левой
части выносим производную ![]() за
скобки:
за
скобки:
![]()
6) И по правилу пропорции сбрасываем эти скобки в знаменатель правой части:
![]()
Производная найдена. Готово.
Интересно
отметить, что в неявном виде можно
переписать любую функцию. Например,
функцию ![]() можно
переписать так:
можно
переписать так: ![]() .
И дифференцировать её по только что
рассмотренному алгоритму. На самом деле
фразы «функция, заданная в неявном виде»
и «неявная функция» отличаются одним
смысловым нюансом. Фраза «функция,
заданная в неявном виде» более общая и
корректная,
.
И дифференцировать её по только что
рассмотренному алгоритму. На самом деле
фразы «функция, заданная в неявном виде»
и «неявная функция» отличаются одним
смысловым нюансом. Фраза «функция,
заданная в неявном виде» более общая и
корректная, ![]() –
эта функция задана в неявном виде, но
здесь можно выразить «игрек» и представить
функцию в явном виде. Под фразой «неявная
функция» понимают «классическую»
неявную функцию, когда «игрек» выразить
нельзя.
–
эта функция задана в неявном виде, но
здесь можно выразить «игрек» и представить
функцию в явном виде. Под фразой «неявная
функция» понимают «классическую»
неявную функцию, когда «игрек» выразить
нельзя.
Второй способ решения
Внимание! Со вторым способом можно ознакомиться только в том случае, если Вы умеете уверенно находить частные производные.
Найдем
производную неявной функции ![]() вторым
способом.
вторым
способом.
Переносим
все слагаемые в левую часть:
![]()
И рассматриваем
функцию двух переменных:
![]()
Тогда нашу
производную можно найти по формуле ![]() Найдем
частные производные:
Найдем
частные производные:
![]()
![]()
Таким
образом:
![]()
Второй способ решения позволяет выполнить проверку. Но оформлять им чистовой вариант задания нежелательно, поскольку частные производные осваивают позже, и студент, изучающий тему «Производная функции одной переменной», знать частные производные как бы еще не должен.
Производная параметрически заданной функции
Не напрягаемся,
в этом параграфе тоже всё достаточно
просто. Можно записать общую формулу
параметрически заданной функции, но,
для того, чтобы было понятно, я сразу
запишу конкретный пример. В параметрической
форме функция задается двумя уравнениями: ![]() .
Частенько уравнения записывают не под
фигурными скобками, а последовательно:
.
Частенько уравнения записывают не под
фигурными скобками, а последовательно:![]() ,
, ![]() .
.
Переменная ![]() называется
параметром и может принимать
значения от «минус бесконечности» до
«плюс бесконечности». Рассмотрим,
например, значение
называется
параметром и может принимать
значения от «минус бесконечности» до
«плюс бесконечности». Рассмотрим,
например, значение ![]() и
подставим его в оба уравнения:
и
подставим его в оба уравнения: ![]() .
Или по человечески: «если икс равен
четырем, то игрек равно единице». На
координатной плоскости можно отметить
точку
.
Или по человечески: «если икс равен
четырем, то игрек равно единице». На
координатной плоскости можно отметить
точку ![]() ,
и эта точка будет соответствовать
значению параметра
,
и эта точка будет соответствовать
значению параметра ![]() .
Аналогично можно найти точку для любого
значения параметра «тэ». Как и для
«обычной» функции, для американских
индейцевпараметрически заданной функции
все права тоже соблюдены: можно построить
график, найти производные и т.д.
.
Аналогично можно найти точку для любого
значения параметра «тэ». Как и для
«обычной» функции, для американских
индейцевпараметрически заданной функции
все права тоже соблюдены: можно построить
график, найти производные и т.д.
В простейших
случаях есть возможность представить
функцию в явном виде. Выразим из первого
уравнения параметр: ![]() –
и подставим его во второе уравнение:
–
и подставим его во второе уравнение: ![]() .
В результате получена обыкновенная
кубическая функция.
.
В результате получена обыкновенная
кубическая функция.
В более «тяжелых» случаях такой фокус не прокатывает. Но это не беда, потому что для нахождения производной параметрической функции существует формула:
![]()
Находим
производную от «игрека по переменной
тэ»:
![]()
Все правила
дифференцирования и таблица производных
справедливы, естественно, и для буквы ![]() ,
таким образом, какой-то новизны в
самом процессе нахождения производных
нет. Просто мысленно замените в таблице
все «иксы» на букву «тэ».
,
таким образом, какой-то новизны в
самом процессе нахождения производных
нет. Просто мысленно замените в таблице
все «иксы» на букву «тэ».
Находим
производную от «икса по переменной
тэ»:
![]()
Теперь
только осталось подставить найденные
производные в нашу формулу:
![]()
Готово.
Производная, как и сама функция, тоже
зависит от параметра ![]() .
.
Что касается
обозначений, то в формуле вместо
записи ![]() можно
было просто записать
можно
было просто записать ![]() без
подстрочного индекса, поскольку это
«обычная» производная «по икс». Но в
литературе всегда встречается вариант
без
подстрочного индекса, поскольку это
«обычная» производная «по икс». Но в
литературе всегда встречается вариант ![]() ,
поэтому я не буду отклоняться от
стандарта.
,
поэтому я не буду отклоняться от
стандарта.
ТЕОРЕМЫ ФЕРМА, РОЛЛЯ, ЛАГРАНЖА И КОШИ
Теорема Ферма. Если функция у = f (х), определенная в интервале (а ; b), достигает в некоторой точке с этого интервала наибольшего (или наименьшего) значения и существует производная f ′(с), то f ′(с) = 0.
Геометрический
смысл этой теоремы состоит в том, что
касательная к графику функции у = f (х)
в точке с абсциссой с параллельна
оси абсцисс (рис.).
 Теорема
Ролля. Если функция у = f (х),
непрерывная на отрезке [а ; b]
и дифференцируемая в интервале
(а ; b), принимает на концах
этого отрезка равные значения f (a)
= f(b), то в интервале (а ; b)
существует такая точка с, что f ′(с)
= 0.
Геометрически эта теорема
означает следующее: если крайние
ординаты кривой у = f (х)
равны, то на кривой найдется точка, в
которой касательная параллельна оси
абсцисс (рис.).
Теорема
Ролля. Если функция у = f (х),
непрерывная на отрезке [а ; b]
и дифференцируемая в интервале
(а ; b), принимает на концах
этого отрезка равные значения f (a)
= f(b), то в интервале (а ; b)
существует такая точка с, что f ′(с)
= 0.
Геометрически эта теорема
означает следующее: если крайние
ординаты кривой у = f (х)
равны, то на кривой найдется точка, в
которой касательная параллельна оси
абсцисс (рис.).
 Теорема
Лагранжа. Если функция у = f (х)
непрерывна на отрезке [а ; b]
и дифференцируема в интервале
(а ; b), то в этом интервале
найдется такая точка с, что
Теорема
Лагранжа. Если функция у = f (х)
непрерывна на отрезке [а ; b]
и дифференцируема в интервале
(а ; b), то в этом интервале
найдется такая точка с, что ![]()
Эта теорема
имеет простой геометрический смысл
(рис.): на графике функции у = f (х)
между точками А и В найдется
такая внутренняя точка С, что
касательная к графику в точке С параллельна
хорде АВ. 
Следствие. Если f ′(x) = 0 в интервале (а ; b), то в этом интервале функция f (х) постоянна.
Теорема Коши. Если функции f (х) и g (х): 1) непрерывны на отрезке [а ; b];
2) дифференцируемы в интервале (а ; b);
3) g'(x) ≠ 0 в этом интервале,
то в интервале (а ; b) существует такая точка с, что имеет место равенство
![]()
|
|
Формула Ньютона-Лейбница (формула двойной подстановки)

(f непрерывна; F - первообразная для f).
Теорема Барроу
Если f непрерывна,
то 
Свойства интеграла Линейность
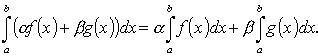
Аддитивность
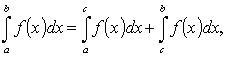

Монотонность
Если ![]() и a
< b, то
и a
< b, то  В
частности, если
В
частности, если ![]() то
то 
Правила Лопиталя. Примеры решений
Представьте
стаю воробьёв с выпученными глазами.
Нет, это не гром, не ураган и даже не
маленький мальчик с рогаткой в руках.
Просто в самую гущу птенчиков летит
огромное-огромное пушечное ядро. Именно
так правила Лопиталя расправляются
с пределами, в которых имеет место
неопределённость ![]() или
или ![]() .
.
Правила Лопиталя – очень мощный метод, позволяющий быстро и эффективно устранить указанные неопределенности, не случайно в сборниках задач, на контрольных работах, зачётах часто встречается устойчивый штамп: «вычислить предел, не пользуясь правилом Лопиталя». Выделенное жирным шрифтом требование можно с чистой совестью приписать и к любому пределу уроков Пределы. Примеры решений, Замечательные пределы.Методы решения пределов, Замечательные эквивалентности, где встречается неопределённость «ноль на ноль» либо «бесконечность на бесконечность». Даже если задание сформулировано коротко – «вычислить пределы», то негласно подразумевается, что вы будете пользоваться всем, чем угодно, но только не правилами Лопиталя.
Всего правил два, и они очень похожи друг на друга, как по сути, так и по способу применения. Кроме непосредственных примеров по теме, мы изучим и дополнительный материал, который будет полезен в ходе дальнейшего изучения математического анализа.
Сразу оговорюсь, что правила будут приведены в лаконичном «практическом» виде, и если вам предстоит сдавать теорию, рекомендую обратиться к учебнику за более строгими выкладками.
Первое правило Лопиталя
Рассмотрим
функции ![]() ,
которые бесконечно малЫ в некоторой
точке
,
которые бесконечно малЫ в некоторой
точке ![]() .
Если существует предел их отношений
.
Если существует предел их отношений ![]() ,
то в целях устранения неопределённости
,
то в целях устранения неопределённости ![]() можно
взять две производные –
от числителя и от знаменателя. При
этом:
можно
взять две производные –
от числителя и от знаменателя. При
этом: ![]() ,
то есть при дифференцировании
числителя и знаменателя значение предела
не меняется.
,
то есть при дифференцировании
числителя и знаменателя значение предела
не меняется.
Примечание:
предел ![]() тоже
должен существовать, в противном случае
правило не применимо.
тоже
должен существовать, в противном случае
правило не применимо.
Что следует из вышесказанного?
Во-первых, необходимо уметь находить производные функций, и чем лучше – тем лучше =)
Во-вторых,
производные берутся ОТДЕЛЬНО от числителя
и ОТДЕЛЬНО от знаменателя. Пожалуйста,
не путайте с правилом дифференцирования
частного  !!!
!!!
И, в-третьих,
«икс» может стремиться куда угодно, в
том числе, к бесконечности – лишь бы
была неопределённость ![]() .
.
Вернёмся
к Примеру 5 первой статьи о пределах,
в котором был получен следующий
результат:
![]() К
неопределённости 0:0 применим первое
правило Лопиталя:
К
неопределённости 0:0 применим первое
правило Лопиталя:
![]() Как
видите, дифференцирование числителя и
знаменателя привело нас к ответу с пол
оборота: нашли две простые производные,
подставили в них «двойку», и оказалось,
что неопределённость бесследно исчезла!
Как
видите, дифференцирование числителя и
знаменателя привело нас к ответу с пол
оборота: нашли две простые производные,
подставили в них «двойку», и оказалось,
что неопределённость бесследно исчезла!
Не редкость,
когда правила Лопиталя приходится
применять последовательно два или
бОльшее количество раз (это относится
и ко второму правилу). Вытащим на
ретро-вечер Пример 2 урока о
замечательных пределах:

На двухъярусной
кровати снова прохлаждаются два бублика.
Применим правило Лопиталя:

Обратите внимание, что на первом шаге в знаменателе берётся производная сложной функции. После этого проводим ряд промежуточных упрощений, в частности, избавляемся от косинуса, указывая, что он стремится к единице. Неопределённость не устранена, поэтому применяем правило Лопиталя ещё раз (вторая строчка).
Я специально подобрал не самый простой пример, чтобы вы провели небольшое самотестирование. Если не совсем понятно, как найдены производные, следует усилить свою технику дифференцирования, если не понятен фокус с косинусом, пожалуйста, вернитесь к замечательным пределам. Не вижу особого смысла в пошаговых комментариях, так как о производных и пределах я уже рассказал достаточно подробно. Новизна статьи состоит в самих правилах и некоторых технических приёмах решения.
Как уже отмечалось, в большинстве случаев правила Лопиталя использовать не нужно, но их зачастую целесообразно применять для черновой проверки решения. Зачастую, но далеко не всегда. Так, например, только что рассмотренный пример значительно выгоднее проверить через замечательные эквивалентности.
Второе правило Лопиталя
Брат-2
борется с двумя спящими восьмёрками ![]() .
Аналогично:
.
Аналогично:
Если
существует предел отношения бесконечно
больших в точке ![]() функций:
функций: ![]() ,
то в целях устранения неопределённости
,
то в целях устранения неопределённости ![]() можно
взять две производные –
ОТДЕЛЬНО от числителя и ОТДЕЛЬНО от
знаменателя. При этом:
можно
взять две производные –
ОТДЕЛЬНО от числителя и ОТДЕЛЬНО от
знаменателя. При этом: ![]() ,
то есть при дифференцировании
числителя и знаменателя значение предела
не меняется.
,
то есть при дифференцировании
числителя и знаменателя значение предела
не меняется.
Примечание:
предел ![]() должен
существовать
должен
существовать
Опять же,
в различных практических
примерах значение ![]() может
быть разным, в том числе, бесконечным.
Важно, чтобы была неопределённость
может
быть разным, в том числе, бесконечным.
Важно, чтобы была неопределённость ![]() .
.
Проверим
Пример №3 первого урока: ![]() .
Используем второе правило Лопиталя:
.
Используем второе правило Лопиталя:
![]()
Однако для
Примера №2 ![]() той
же статьи проверка данным способом
будет весьма муторна. Тут придётся
использовать правило Лопиталя три раза
подряд (экспериментаторы могут
попробовать). На самом деле ответ лежит
на поверхности и почти мгновенно
определяется устно (см. статью Методы
решения пределов).
той
же статьи проверка данным способом
будет весьма муторна. Тут придётся
использовать правило Лопиталя три раза
подряд (экспериментаторы могут
попробовать). На самом деле ответ лежит
на поверхности и почти мгновенно
определяется устно (см. статью Методы
решения пределов).
Коль скоро речь зашла о великанах, разберём два каноничных предела:
Пример 1
Вычислить
предел
![]()
Получить
ответ «обычными» методами непросто,
поэтому для раскрытия неопределённости
«бесконечность на бесконечность»
используем правило Лопиталя:

Таким
образом, линейная функция более
высокого порядка роста, чем логарифм с
основанием бОльшим единицы (![]() и
т.д.). Разумеется, «иксы» в старших
степенях тоже будут «перетягивать»
такие логарифмы. Действительно,
функция
и
т.д.). Разумеется, «иксы» в старших
степенях тоже будут «перетягивать»
такие логарифмы. Действительно,
функция ![]() растёт
достаточно медленно и её график является
более пологим относительно того же
«икса».
растёт
достаточно медленно и её график является
более пологим относительно того же
«икса».
Пример 2
Вычислить
предел
![]()
Ещё один
примелькавшийся кадр. В целях устранения
неопределённости ![]() ,
используем правило Лопиталя, причём,
два раза подряд:
,
используем правило Лопиталя, причём,
два раза подряд:
![]()
Показательная
функция, с основанием, бОльшим единицы (![]() и
т.д.) более высокого порядка роста,
чем степенная функция с положительной
степенью.
и
т.д.) более высокого порядка роста,
чем степенная функция с положительной
степенью.
Похожие пределы встречаются в ходе полного исследования функции, а именно, при нахождении асимптот графиков. Также замечаются они и в некоторых задачах по теории вероятностей. Советую взять на заметку два рассмотренных примера, это один из немногих случаев, когда лучше дифференцирования числителя и знаменателя ничего нет.
Далее по тексту я не буду разграничивать первое и второе правило Лопиталя, это было сделано только в целях структурирования статьи. Вообще, с моей точки зрения, несколько вредно излишне нумеровать математические аксиомы, теоремы, правила, свойства, поскольку фразы вроде «согласно следствию 3 по теореме 19…» информативны только в рамках того или иного учебника. В другом источнике информации то же самое будет «следствием 2 и теоремой 3». Такие высказывания формальны и удобны разве что самим авторам. В идеале лучше ссылаться на суть математического факта. Исключение – исторически устоявшиеся термины, например, первый замечательный предел или второй замечательный предел.
Продолжаем разрабатывать тему, которую нам подкинул член Парижской академии наук маркиз Гийом Франсуа де Лопиталь. Статья приобретает ярко выраженную практическую окраску и в достаточно распространённом задании требуется:
Вычислить предел, используя правило Лопиталя
Для разминки разберёмся с парой небольших воробушков:
Пример 3
Вычислить
предел по правилу Лопиталя
![]()
Предел
можно предварительно упростить,
избавившись от косинуса, однако проявим
уважение к условию и сразу продифференцируем
числитель и знаменатель:
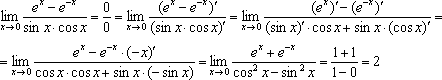
В самом
процессе нахождения производных нет
чего-то нестандартного, так, в знаменателе
использовано обычное правило
дифференцирования произведения ![]() .
.
Рассмотренный пример разруливается и через замечательные пределы, похожий случай разобран в конце статьи Сложные пределы.
Пример 4
Вычислить
предел по правилу Лопиталя
![]()
Это пример для самостоятельного решения. Нормально пошутил =)
Типична ситуация, когда после дифференцирования получаются трех- или четырёхэтажные дроби:
Пример 5
Вычислить
предел, используя правило Лопиталя
![]()
Напрашивается
применение замечательной
эквивалентности, но путь жёстко
предопределён по условию:
 После
дифференцирования настоятельно
рекомендую избавляться от многоэтажности
дроби и проводить максимальные
упрощения. Конечно, более подготовленные
студенты могут пропустить последний
шаг и сразу записать:
После
дифференцирования настоятельно
рекомендую избавляться от многоэтажности
дроби и проводить максимальные
упрощения. Конечно, более подготовленные
студенты могут пропустить последний
шаг и сразу записать:  ,
но в некоторых пределах запутаются даже
отличники.
,
но в некоторых пределах запутаются даже
отличники.
Пример 6
Вычислить
предел, используя правило Лопиталя
![]()
Пример 7
Вычислить
предел, используя правило Лопиталя
![]()
Это примеры для самостоятельного решения. В Примере 7 можно ничего не упрощать, слишком уж простой получается после дифференцирования дробь. А вот в Примере 8 после применения правила Лопиталя крайне желательно избавиться от трёхэтажности, поскольку вычисления будут не самыми удобными. Полное решение и ответ в конце урока. Если возникли затруднения – тригонометрическая таблица в помощь.
И, упрощения совершенно необходимы, когда после дифференцирования неопределённостьне устранена.
Пример 8
Вычислить
предел, используя правило Лопиталя
![]()
Поехали:

Интересно,
что первоначальная неопределённость ![]() после
первого дифференцирования превратилась
в неопределённость
после
первого дифференцирования превратилась
в неопределённость ![]() ,
и правило Лопиталя невозмутимо применяется
дальше. Также заметьте, как после каждого
«подхода» устраняется четырёхэтажная
дробь, а константы выносятся за знак
предела. В более простых примерах
константы удобнее не выносить, но когда
предел сложный, упрощаем всё-всё-всё.
Коварство решённого примера состоит
ещё и в том, что при
,
и правило Лопиталя невозмутимо применяется
дальше. Также заметьте, как после каждого
«подхода» устраняется четырёхэтажная
дробь, а константы выносятся за знак
предела. В более простых примерах
константы удобнее не выносить, но когда
предел сложный, упрощаем всё-всё-всё.
Коварство решённого примера состоит
ещё и в том, что при ![]() ,
а
,
а ![]() ,
поэтому в ходе ликвидации синусов
немудрено запутаться в знаках. В
предпоследней строчке синусы можно
было и не убивать, но пример довольно
тяжелый, простительно.
,
поэтому в ходе ликвидации синусов
немудрено запутаться в знаках. В
предпоследней строчке синусы можно
было и не убивать, но пример довольно
тяжелый, простительно.
На днях мне попалось любопытное задание:
Пример 9
Вычислить
предел функции, используя правило
Лопиталя
![]()
Если честно, немного засомневался, чему будет равен данный предел. Как демонстрировалось выше, «икс» более высокого порядка роста, чем логарифм, но «перетянет» ли он логарифм в кубе? Постарайтесь выяснить самостоятельно, за кем будет победа.
Да, правила Лопиталя – это не только пальба по воробьям из пушки, но ещё и кропотливая работа….
В целях
применения правил Лопиталя к бубликам
или уставшим восьмёркам сводятся
неопределённости вида ![]() .
.
Расправа
с неопределённостью ![]() подробно
разобрана в Примерах №№9-13 урока Методы
решения пределов. Давайте для проформы
ещё один:
подробно
разобрана в Примерах №№9-13 урока Методы
решения пределов. Давайте для проформы
ещё один:
Пример 10
Вычислить
предел функции, используя правило
Лопиталя
![]()
На первом
шаге приводим выражение к общему
знаменателю, трансформируя тем самым
неопределённость ![]() в
неопределённость
в
неопределённость ![]() .
А затем заряжаем правило Лопиталя:
.
А затем заряжаем правило Лопиталя:

Здесь, к слову, тот случай, когда четырёхэтажное выражение трогать бессмысленно.
Неопределённость ![]() тоже
не сопротивляется превращению в
тоже
не сопротивляется превращению в ![]() или
или ![]() :
:
Пример 11
Вычислить
предел функции с помощью правила
Лопиталя
![]()
Предел
здесь односторонний, и о таких пределах
уже шла речь в методичке Графики и
свойства функций. Как вы помните,
графика «классического» логарифма не
существует слева от оси ![]() ,
таким образом, мы можем приближаться к
нулю только справа.
,
таким образом, мы можем приближаться к
нулю только справа.
Правила
Лопиталя для односторонних пределов
работают, но сначала необходимо
разобраться с неопределённостью ![]() .
На первом шаге делаем дробь трёхэтажной,
получая неопределённость
.
На первом шаге делаем дробь трёхэтажной,
получая неопределённость ![]() ,
далее решение идёт по шаблонной схеме:
,
далее решение идёт по шаблонной схеме:

После
дифференцирования числителя и знаменателя
избавляемся от четырёхэтажной дроби,
чтобы провести упрощения. В результате
нарисовалась неопределённость ![]() .
Повторяем трюк: снова делаем дробь
трёхэтажной и к полученной
неопределённости
.
Повторяем трюк: снова делаем дробь
трёхэтажной и к полученной
неопределённости ![]() применяем
правило Лопиталя ещё раз:
применяем
правило Лопиталя ещё раз:
 Готово.
Готово.
Исходный
предел можно было попытаться свести к
двум бубликам:
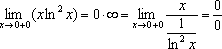 Но,
во-первых, производная в знаменателе
труднее, а во-вторых, ничего хорошего
из этого не выйдет.
Но,
во-первых, производная в знаменателе
труднее, а во-вторых, ничего хорошего
из этого не выйдет.
Таким
образом, перед решением похожих
примеров нужно проанализировать (устно
либо на черновике), К КАКОЙ неопределённости
выгоднее свести ![]() –
к «нулю на ноль» или к «бесконечности
на бесконечность».
–
к «нулю на ноль» или к «бесконечности
на бесконечность».
В свою
очередь на огонёк ![]() подтягиваются собутыльники
подтягиваются собутыльники ![]() и
более экзотические товарищи
и
более экзотические товарищи ![]() .
Метод трансформации прост и стандартен:
.
Метод трансформации прост и стандартен:
Пример 12
Вычислить
предел функции с помощью правила
Лопиталя
![]()
Для устранения
неопределённости ![]() используем
основное логарифмическое тождество:
используем
основное логарифмическое тождество: ![]() .
В данном случае
.
В данном случае ![]() :
:
![]()
На
предпоследнем шаге, согласно
известному школьному свойству,
«сносим» синус из степени за пределы
логарифма, получая произведение ![]() .
На последнем шаге перемещаем значок
предела в показатель (поскольку
экспоненциальная функция непрерывна,
да и предел относится, прежде всего, к
верхнему этажу).
.
На последнем шаге перемещаем значок
предела в показатель (поскольку
экспоненциальная функция непрерывна,
да и предел относится, прежде всего, к
верхнему этажу).
Чтобы не
мельчить, вычислим предел показателя
отдельно:
![]()
С
неопределённостью ![]() разбираемся
уже знакомым способом – делаем дробь
трёхэтажной, получая долгожданную
неопределённость
разбираемся
уже знакомым способом – делаем дробь
трёхэтажной, получая долгожданную
неопределённость ![]() ,
к которой применимо правило Лопиталя:
,
к которой применимо правило Лопиталя:

Метаморфозы
продолжаются, теперь вылезла
неопределённость «ноль на ноль». В
принципе, можно избавиться от косинуса,
указав, что он стремится к единице. Но
мудрая стратегия заключается в том,
чтобы никто ни до чего не докопался.
Поэтому сразу применим правило Лопиталя,
как этого требует условие задачи:
![]()
Не торопитесь,
предел не равен нулю! Мы вычислили только
предел показателя. В конце решения
главное не забыть про экспоненту, я
сейчас сам чуть про неё не забыл =)
Окончательно:
![]()
В ряде
случаев после использование основного
логарифмического тождества удаётся
миновать неопределённость ![]() :
:
Пример 13
Вычислить
предел по правилу Лопиталя
![]()
Очередной
папуас ![]() тоже
сдаётся перед формулой
тоже
сдаётся перед формулой ![]() .
В данном случае
.
В данном случае ![]() :
:
![]()
В результате
сразу получена неопределённость ![]() ,
что облегчает задачу. Предел показателя
для удобства вычислим отдельно:
,
что облегчает задачу. Предел показателя
для удобства вычислим отдельно:
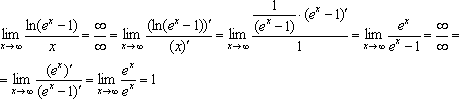
В итоге:
![]()
Аналогичное задание для самостоятельного решения:
Пример 14
Вычислить
предел по правилу Лопиталя
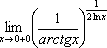
Полное решение и ответ в конце урока.
Предел с
неопределённостью ![]() по
правилу Лопиталя, если честно, у себя
не нашёл, но для полноты картины решим
многострадальный шестой пример
урока Замечательные пределы:
по
правилу Лопиталя, если честно, у себя
не нашёл, но для полноты картины решим
многострадальный шестой пример
урока Замечательные пределы:
Пример 15
Вычислить
с помощью правила Лопиталя
![]()
Решайте =)
В заключение хочу успокоить гринписовцев – ни один воробей от оружия серьёзно не пострадал, пределы – птицы юркие, да и ядра формы обтекаемой. Вспоминаем обычное требование: «…не пользуясь правилом Лопиталя». С беспощадной действительностью соприкоснёмся в статье Сложные пределы.
Теорема Штольца
Содержание
работы: Формулировка и доказательство
теоремы Штольца. Применение теоремы
Штольца: ![]() ;
нахождение предела “среднего
арифметического” первых n значений
варианты
;
нахождение предела “среднего
арифметического” первых n значений
варианты ![]() ;
; ![]() ;
; ![]() .
Применение теоремы Штольца к нахождению
некоторых пределов отношения
последовательностей. Нахождение
некоторых пределов отношения функций
с помощью теоремы Штольца.
.
Применение теоремы Штольца к нахождению
некоторых пределов отношения
последовательностей. Нахождение
некоторых пределов отношения функций
с помощью теоремы Штольца.
Для
определения пределов неопределенных
выражений ![]() типа
типа ![]() часто
бывает полезна следующая теорема,
принадлежащая Штольцу.
часто
бывает полезна следующая теорема,
принадлежащая Штольцу.
Пусть
варианта ![]() ,
причем – хотя бы начиная с некоторого
листа – с возрастанием n и
,
причем – хотя бы начиная с некоторого
листа – с возрастанием n и ![]() возрастает:
возрастает: ![]() .
Тогда
.
Тогда ![]() =
=![]() ,
,
Если только существует предел справа (конечный или даже бесконечный).
Допустим,
что этот предел равен конечному числу ![]() :
:
![]() .
.
Тогда по
любому заданному ![]() найдется
такой номер N, что для n>N будет
найдется
такой номер N, что для n>N будет

или
![]() .
.
Значит,
какое бы n>N ни взять, все дроби ![]() ,
, ![]() ,
…,
,
…, ![]() ,
, ![]() лежат
между этими границами. Так как знаменатели
их, ввиду возрастания yn вместе с номером
n, положительны, то между теми же границами
содержится и дробь
лежат
между этими границами. Так как знаменатели
их, ввиду возрастания yn вместе с номером
n, положительны, то между теми же границами
содержится и дробь ![]() ,
числитель которой есть сумма всех
числителей, написанных выше дробей, а
знаменатель – сумма всех знаменателей.
Итак, при n>N
,
числитель которой есть сумма всех
числителей, написанных выше дробей, а
знаменатель – сумма всех знаменателей.
Итак, при n>N
 .
.
Напишем теперь тождество:
 ,
,
откуда
 .
.
Второе
слагаемое справа при n>N становится
<![]() ;
первое же слагаемое, ввиду того, что
;
первое же слагаемое, ввиду того, что ![]() ,
также будет <
,
также будет <![]() ,
скажем, для n>N’. Если при этом взять
N’>N, то для n>N’, очевидно,
,
скажем, для n>N’. Если при этом взять
N’>N, то для n>N’, очевидно,  ,
что и доказывает наше утверждение.
,
что и доказывает наше утверждение.
Примеры: Пусть,
например, ![]() .
Отсюда, прежде всего вытекает, что (для
достаточно больших n)
.
Отсюда, прежде всего вытекает, что (для
достаточно больших n) ![]() ,
следовательно, вместе с yn и xn
,
следовательно, вместе с yn и xn![]() ,
причем варианта xn возрастает с возрастанием
номера n. В таком случае, доказанную
теорему можно применить к обратному
отношению
,
причем варианта xn возрастает с возрастанием
номера n. В таком случае, доказанную
теорему можно применить к обратному
отношению ![]()
![]()
(ибо здесь
предел уже конечен), откуда и следует,
что ![]() ,
что и требовалось доказать.
,
что и требовалось доказать.
При а>1
![]()
Этот
результат с помощью теоремы Штольца
получается сразу:![]()
![]()
Применим теорему Штольца к доказательству следующего интересного предложения:
Если варианта
an![]() имеет
предел (конечный или бесконечный), то
этот же предел имеет и варианта
имеет
предел (конечный или бесконечный), то
этот же предел имеет и варианта
![]()
(“среднее арифметическое” первых n значений варианты аn).
Действительно, полагая в теореме Штольца
Xn=a1+a2+…+an, yn=n,
Имеем:
![]()
Например,
если мы знаем, что ![]() ,
,
то и ![]()
Рассмотрим теперь варианту (считая k-натуральным)
![]() ,
,
которая
представляет неопределённость вида ![]() .
.
Полагая в теореме Штольца
xn=1k+2k+…+nk, yn=nk+1,
будем иметь
![]() .
.
Но
(n-1)k+1=nk+1-(k+1)nk+… ,
так что
nk+1-(n-1)k+1=(k+1)nk+…
и
![]() .
.
Определим предел варианты
![]() ,
,
представляющей
в первой форме неопределенность вида ![]() ,
а во второй – вида
,
а во второй – вида ![]() .
Произведя вычитание дробей, получим на
этот раз неопределенное выражение
вида
.
Произведя вычитание дробей, получим на
этот раз неопределенное выражение
вида ![]() :
:
![]() .
.
Полагая xn равным числителю этой дроби, а yn – знаменателю, применим еще раз ту же теорему. Получим
![]() .
.
Но ![]() ,
,
а ![]() ,
,
так что, окончательно,
 .
.
Пример 1.
![]() =
=![]() =
=![]() =
=![]() =
=![]() =
=![]() =
= ![]() =
=![]()
![]() =
=![]() =
=![]() .
.
Пример 2.
![]() =
=
=![]() =
=
=![]() =
=
=![]() =
=
=![]() =
=
=![]() =
=
=![]() .
.
Пример 3.
![]()
=![]()
=![]() .
.
Теорема Штольца справедлива для последовательностей, но т.к. последовательности есть частный случай функций, то эту теорему можно обобщить для функций.
Теорема.
Пусть
функция ![]() ,
причем, начиная с некоторой xk, g(xk+1)>g(xk),
т.е. функция возрастающая.
,
причем, начиная с некоторой xk, g(xk+1)>g(xk),
т.е. функция возрастающая.
Тогда ![]() ,
,
если только существует предел справа конечный или бесконечный.
Доказательство:
Допустим, что этот предел равен конечному числу k
![]() .
.
Тогда, по
определению предела ![]()

или
![]() .
.
Значит,
какой бы ![]() ни
взять, все дроби
ни
взять, все дроби
![]() ,
, ![]() ,
…,
,
…, ![]()
лежат между
этими границами. Так как знаменатели
их, ввиду возрастания g(xn) вместе с x(n),
положительны, то между теми же границами
содержится и дробь ![]() ,
числитель которой есть сумма всех
числителей, написанных выше дробей, а
знаменатель – сумма всех знаменателей.
Итак, при
,
числитель которой есть сумма всех
числителей, написанных выше дробей, а
знаменатель – сумма всех знаменателей.
Итак, при ![]()
 .
.
Напишем тождество(которое легко проверить):
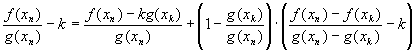 ,
,
Откуда
 .
.
Второе
слагаемое справа при ![]() становится
становится ![]() ;
первое же слагаемое, ввиду того, что
;
первое же слагаемое, ввиду того, что ![]() ,
так же будет
,
так же будет ![]() ,
скажем, для
,
скажем, для ![]() .
Если при этом взять
.
Если при этом взять ![]() ,
то для
,
то для ![]() ,
очевидно
,
очевидно  ,
что и доказывает теорему.
,
что и доказывает теорему.
Примеры:
Найти следующие пределы:
![]() очевидна
неопределенность
очевидна
неопределенность ![]()
![]() =
=![]() =
=![]() =2
=2
![]() неопределенность
неопределенность ![]()
![]() =
=![]() =
=![]() =
=![]() =0
=0
![]() неопределенность
неопределенность ![]()
![]() =
=![]() =
=![]() =
=![]()
Асимптоты графика функции
Призрак асимптоты давно бродил по сайту чтобы, наконец, материализоваться в отдельно взятой статье и привести в особый восторг читателей, озадаченных полным исследованием функции. Нахождение асимптот графика – одна из немногих частей указанного задания, которая освещается в школьном курсе лишь в обзорном порядке, поскольку события вращаются вокруг вычисления пределов функций, а они относятся всё-таки к высшей математике. Посетители, слабо разбирающиеся в математическом анализе, намёк, думаю, понятен ;-) …стоп-стоп, вы куда? Пределы – это легко!
Примеры асимптот встретились сразу же на первом уроке о графиках элементарных функций, и сейчас тема получает детальное рассмотрение.
Итак, что такое асимптота?
Асимптота – это прямая, к которой бесконечно близко приближается график функции, при этом он должен бесконечно далеко удаляться от начала координат.
Примечание: определение содержательно, если вам необходима формулировка в терминах и обозначениях математического анализа, пожалуйста, обратитесь к учебнику.
На плоскости асимптоты классифицируют по их естественному расположению:
1) Вертикальные
асимптоты, которые задаются уравнением
вида ![]() ,
где «альфа» – действительное число.
Популярная представительница
,
где «альфа» – действительное число.
Популярная представительница ![]() определяет
саму ось ординат,
с приступом лёгкой
тошноты вспоминаем гиперболу
определяет
саму ось ординат,
с приступом лёгкой
тошноты вспоминаем гиперболу ![]() .
.
2) Наклонные
асимптоты традиционно
записываются уравнением
прямой с угловым коэффициентом ![]() .
Иногда отдельной группой выделяют
частный случай –горизонтальные
асимптоты
.
Иногда отдельной группой выделяют
частный случай –горизонтальные
асимптоты ![]() .
Например, та же гипербола с асимптотой
.
Например, та же гипербола с асимптотой ![]() .
.
Резво пошло-поехало, ударим по теме короткой автоматной очередью:
Сколько асимптот может быть у графика функции?
Ни одной, одна, две, три,… или бесконечно много. За примерами далеко ходить не будем, вспомним элементарные функции. Парабола, кубическая парабола, синусоида вовсе не имеют асимптот. График экспоненциальной, логарифмической функции обладает единственной асимптотой. У арктангенса, арккотангенса их две, а у тангенса, котангенса – бесконечно много. Не редкость, когда график укомплектован и горизонтальными и вертикальными асимптотами. Гипербола, will always love you.
Что значит найти асимптоты графика функции?
Это значит выяснить их уравнения, ну и начертить прямые линии, если того требует условие задачи. Процесс предполагает нахождение пределов функции.
Вертикальные асимптоты графика функции
Вертикальная
асимптота графика, как правило, находится в
точке бесконечного разрывафункции.
Всё просто: если в точке ![]() функция
функция ![]() терпит
бесконечный разрыв, то прямая,
заданная уравнением
терпит
бесконечный разрыв, то прямая,
заданная уравнением ![]() является
вертикальной асимптотой графика.
является
вертикальной асимптотой графика.
Примечание:
обратите внимание, что запись ![]() используется
для обозначения двух совершенно разных
понятий. Точка подразумевается или
уравнение прямой – зависит от контекста.
используется
для обозначения двух совершенно разных
понятий. Точка подразумевается или
уравнение прямой – зависит от контекста.
Таким
образом, чтобы установить наличие
вертикальной асимптоты ![]() в
точке
в
точке ![]() достаточно
показать, что хотя бы один из
односторонних пределов
достаточно
показать, что хотя бы один из
односторонних пределов ![]() бесконечен.
Чаще всего это точка, где знаменатель
функции равен нулю. По существу, мы уже
находили вертикальные асимптоты в
последних примерах урока о
непрерывности функции. Но в ряде
случаев существует только один
односторонний предел, и, если он
бесконечен, то снова – любите и жалуйте
вертикальную асимптоту. Простейшая
иллюстрация:
бесконечен.
Чаще всего это точка, где знаменатель
функции равен нулю. По существу, мы уже
находили вертикальные асимптоты в
последних примерах урока о
непрерывности функции. Но в ряде
случаев существует только один
односторонний предел, и, если он
бесконечен, то снова – любите и жалуйте
вертикальную асимптоту. Простейшая
иллюстрация: ![]() и
ось ординат (см. Графики
и свойства элементарных функций).
и
ось ординат (см. Графики
и свойства элементарных функций).
Из
вышесказанного также следует очевидный
факт: если функция непрерывна на ![]() ,
то вертикальные асимптоты отсутствуют.
На ум почему-то пришла парабола.
Действительно, где тут «воткнёшь»
прямую? …да… понимаю… последователи
дядюшки Фрейда забились в истерике
=)
Обратное утверждение в общем
случае неверно: так, функция
,
то вертикальные асимптоты отсутствуют.
На ум почему-то пришла парабола.
Действительно, где тут «воткнёшь»
прямую? …да… понимаю… последователи
дядюшки Фрейда забились в истерике
=)
Обратное утверждение в общем
случае неверно: так, функция ![]() не
определена на всей числовой прямой,
однако совершенно обделена асимптотами.
не
определена на всей числовой прямой,
однако совершенно обделена асимптотами.
Наклонные асимптоты графика функции
Наклонные
(как частный случай – горизонтальные)
асимптоты могут нарисоваться, если
функция стремится к «плюс бесконечности»
или/и «минус бесконечности». Поэтому график
функции не может иметь больше 2-х наклонных
асимптот. Например, график экспоненциальной
функции ![]() обладает
единственной горизонтальной асимптотой
при
обладает
единственной горизонтальной асимптотой
при ![]() ,
а график арктангенса
,
а график арктангенса ![]() при
при ![]() –
двумя такими асимптотами, причём
различными.
–
двумя такими асимптотами, причём
различными.
Когда график
и там и там сближается с единственной
наклонной асимптотой, то «бесконечности»
принято объединять под единой записью ![]() .
Например, …правильно догадались:
.
Например, …правильно догадались: ![]() .
.
Общее практическое правило:
Если
существуют два конечных предела ![]() ,
то прямая
,
то прямая ![]() является
наклонной асимптотой графика
функции
является
наклонной асимптотой графика
функции ![]() при
при ![]() .
Если хотя бы один из перечисленных
пределов бесконечен, то наклонная
асимптота отсутствует.
.
Если хотя бы один из перечисленных
пределов бесконечен, то наклонная
асимптота отсутствует.
Примечание: формулы остаются справедливыми, если «икс» стремится только к «плюс бесконечности» или только к «минус бесконечности».
Докажем,
что у параболы ![]() нет
наклонных асимптот:
нет
наклонных асимптот:
![]()
Предел
бесконечен, значит, наклонная асимптота
отсутствует. Заметьте, что в нахождении
предела ![]() необходимость
отпала, поскольку ответ уже получен.
необходимость
отпала, поскольку ответ уже получен.
Примечание: если у вас возникли (или возникнут) трудности с пониманием знаков «плюс-минус», «минус-плюс», пожалуйста, посмотрите справку в начале урока о бесконечно малых функциях, где я рассказал, как правильно интерпретировать данные знаки.
Очевидно, что у любой квадратичной, кубической функции, многочлена 4-ой и высших степеней также нет наклонных асимптот.
А теперь
убедимся, что при ![]() у
графика
у
графика ![]() тоже
нет наклонной асимптоты. Для раскрытия
неопределённости используем правило
Лопиталя:
тоже
нет наклонной асимптоты. Для раскрытия
неопределённости используем правило
Лопиталя:
![]() ,
что и требовалось проверить.
,
что и требовалось проверить.
При ![]() функция
функция ![]() неограниченно
растёт, однако не существует такой
прямой, к которой бы её график
приближался бесконечно близко.
неограниченно
растёт, однако не существует такой
прямой, к которой бы её график
приближался бесконечно близко.
Переходим к практической части урока:
Как найти асимптоты графика функции?
Именно так формулируется типовое задание, и оно предполагает нахождение ВСЕХ асимптот графика (вертикальных, наклонных/горизонтальных). Хотя, если быть более точным в постановке вопроса – речь идёт об исследовании на наличие асимптот (ведь таковых может и вовсе не оказаться). Начнём с чего-нибудь простого:
Пример 1
Найти
асимптоты графика функции
![]()
Решение удобно разбить на два пункта:
1) Сначала
проверяем, есть ли вертикальные асимптоты.
Знаменатель обращается в ноль при ![]() ,
и сразу понятно, что в данной точке
функция терпит бесконечный
разрыв, а прямая, заданная уравнением
,
и сразу понятно, что в данной точке
функция терпит бесконечный
разрыв, а прямая, заданная уравнением ![]() ,
является вертикальной асимптотой
графика функции
,
является вертикальной асимптотой
графика функции ![]() .
Но, прежде чем оформить такой вывод,
необходимо найти односторонние пределы:
.
Но, прежде чем оформить такой вывод,
необходимо найти односторонние пределы:
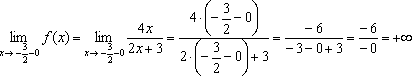
Напоминаю
технику вычислений, на которой я подобно
останавливался в статьеНепрерывность
функции. Точки разрыва. В выражение
под знаком предела вместо «икса»
подставляем ![]() .
В числителе ничего интересного:
.
В числителе ничего интересного:
![]() .
.
А вот в
знаменателе получается бесконечно
малое отрицательное число:
![]() ,
оно и определяет судьбу предела.
,
оно и определяет судьбу предела.
Левосторонний
предел бесконечный, и, в принципе уже
можно вынести вердикт о наличии
вертикальной асимптоты. Но односторонние
пределы нужны не только для этого – они
ПОМОГАЮТ ПОНЯТЬ, КАК расположен
график функции и построить его КОРРЕКТНО.
Поэтому обязательно вычислим и
правосторонний предел:

Вывод:
односторонние пределы бесконечны,
значит, прямая ![]() является
вертикальной асимптотой графика функции
при
является
вертикальной асимптотой графика функции
при ![]() .
.
2) Проверим
наличие наклонных асимптот:

Первый
предел конечен, значит, необходимо
«продолжить разговор» и найти второй
предел:
 Второй
предел тоже конечен.
Второй
предел тоже конечен.
Таким
образом, наша асимптота:

Вывод:
прямая, заданная уравнением ![]() является
горизонтальной асимптотой графика
функции при
является
горизонтальной асимптотой графика
функции при ![]() .
.
Для нахождения горизонтальной асимптоты можно пользоваться упрощенной формулой:
Если
существует конечный предел ![]() ,
то прямая
,
то прямая ![]() является
горизонтальной асимптотой графика
функции
является
горизонтальной асимптотой графика
функции ![]() при
при ![]() .
.
Нетрудно
заметить, что числитель и знаменатель
функции ![]() одного
порядка роста, а значит, искомый
предел будет конечным:
одного
порядка роста, а значит, искомый
предел будет конечным:

Ответ: ![]()
По условию
не нужно выполнять чертёж, но если в
самом разгаре исследование
функции, то на черновике сразу же
делаем набросок:
 Исходя
из трёх найденных пределов
Исходя
из трёх найденных пределов ![]() ,
попытайтесь самостоятельно прикинуть,
как может располагаться график функции
,
попытайтесь самостоятельно прикинуть,
как может располагаться график функции ![]() .
Совсем трудно? Найдите 5-6-7-8 точек и
отметьте их на чертеже. Впрочем, график
данной функции строится с
помощью преобразований
графика элементарной функции, и
читатели, внимательно рассмотревшие
Пример 21 указанной статьи легко
догадаются, что это за кривая.
.
Совсем трудно? Найдите 5-6-7-8 точек и
отметьте их на чертеже. Впрочем, график
данной функции строится с
помощью преобразований
графика элементарной функции, и
читатели, внимательно рассмотревшие
Пример 21 указанной статьи легко
догадаются, что это за кривая.
Пример 2
Найти
асимптоты графика функции
![]()
Это пример для самостоятельного решения. Процесс, напоминаю, удобно разбить на два пункта – вертикальные асимптоты и наклонные асимптоты. В образце решения горизонтальная асимптота найдёна по упрощенной схеме.
На практике чаще всего встречаются дробно-рациональные функции, и после тренировки на гиперболах усложним задание:
Пример 3
Найти
асимптоты графика функции
![]()
Решение: Раз, два и готово:
1) Вертикальные
асимптоты находятся в
точках бесконечного разрыва, поэтому
нужно проверить, обращается ли знаменатель
в ноль. Решим квадратное
уравнение:
![]() Дискриминант
положителен, поэтому уравнение имеет
два действительных корня, и работы
значительно прибавляется =)
Дискриминант
положителен, поэтому уравнение имеет
два действительных корня, и работы
значительно прибавляется =)

В целях
дальнейшего нахождения односторонних
пределов квадратный трёхчлен удобно
разложить на множители:
![]() (для
компактной записи «минус» внесли в
первую скобку). Для подстраховки выполним
проверку, мысленно либо на черновике
раскрыв скобки.
(для
компактной записи «минус» внесли в
первую скобку). Для подстраховки выполним
проверку, мысленно либо на черновике
раскрыв скобки.
Перепишем
функцию в виде ![]()
Найдём
односторонние пределы в точке ![]() :
:

И в точке ![]() :
:

Таким
образом, прямые ![]() являются
вертикальными асимптотами графика
рассматриваемой функции.
являются
вертикальными асимптотами графика
рассматриваемой функции.
2) Если
посмотреть на функцию ![]() ,
то совершенно очевидно, что предел
,
то совершенно очевидно, что предел ![]() будет
конечным и у нас горизонтальная асимптота.
Покажем её наличие коротким способом:
будет
конечным и у нас горизонтальная асимптота.
Покажем её наличие коротким способом:
![]()
Таким
образом, прямая ![]() (ось
абсцисс) является горизонтальной
асимптотой графика данной функции.
(ось
абсцисс) является горизонтальной
асимптотой графика данной функции.
Ответ: ![]()
Найденные
пределы и асимптоты дают немало информации
о графике функции. Постарайтесь мысленно
представить чертёж с учётом следующих
фактов:

Схематично изобразите вашу версию графика на черновике.
Конечно, найденные пределы однозначно не определяют вид графика, и возможно, вы допустите ошибку, но само упражнение окажет неоценимую помощь в ходе полного исследования функции. Правильная картинка – в конце урока.
Пример 4
Найти
асимптоты графика функции
![]()
Пример 5
Найти
асимптоты графика функции
![]() Это
задания для самостоятельного решения.
Оба графика снова обладают горизонтальными
асимптотами, которые немедленно
детектируются по следующим признакам:
в Примере 4порядок
роста знаменателя больше,
чем порядок роста числителя, а в Примере
5 числитель и знаменатель одного
порядка роста. В образце решения
первая функция исследована на наличие
наклонных асимптот полным путём, а
вторая – через предел
Это
задания для самостоятельного решения.
Оба графика снова обладают горизонтальными
асимптотами, которые немедленно
детектируются по следующим признакам:
в Примере 4порядок
роста знаменателя больше,
чем порядок роста числителя, а в Примере
5 числитель и знаменатель одного
порядка роста. В образце решения
первая функция исследована на наличие
наклонных асимптот полным путём, а
вторая – через предел ![]() .
.
Горизонтальные асимптоты, по моему субъективному впечатлению, встречаются заметно чаще, чем те, которые «по-настоящему наклонены». Долгожданный общий случай:
Пример 6
Найти
асимптоты графика функции
![]()
Решение: классика жанра:
1) Поскольку знаменатель положителен, то функция непрерывна на всей числовой прямой, и вертикальные асимптоты отсутствуют. …Хорошо ли это? Не то слово – отлично! Пункт №1 закрыт.
2) Проверим
наличие наклонных асимптот:
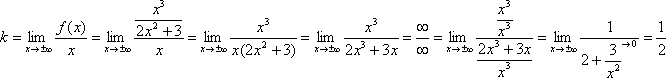 Первый
предел конечен, поэтому едем
дальше. В ходе вычисления второго предела
для устранения неопределённости
«бесконечность минус бесконечность» приводим
выражение к общему знаменателю:
Первый
предел конечен, поэтому едем
дальше. В ходе вычисления второго предела
для устранения неопределённости
«бесконечность минус бесконечность» приводим
выражение к общему знаменателю:

Второй
предел тоже конечен, следовательно,
у графика рассматриваемой функции
существует наклонная асимптота:

Вывод: ![]()
Таким
образом, при ![]() график
функции
график
функции ![]() бесконечно
близко приближается к прямой
бесконечно
близко приближается к прямой ![]() :
:

Заметьте, что он пересекает свою наклонную асимптоту в начале координат, и такие точки пересечения вполне допустимы – важно, чтобы «всё было нормально» на бесконечности (собственно, речь об асимптотах и заходит именно там).
Пример 7
Найти
асимптоты графика функции
![]()
Решение: комментировать особо нечего, поэтому оформлю примерный образец чистового решения:
1) Вертикальные
асимптоты. Исследуем точку ![]() .
.
 Прямая
Прямая ![]() является
вертикальной асимптотой для графика
является
вертикальной асимптотой для графика ![]() при
при ![]() .
.
2) Наклонные
асимптоты:

Прямая ![]() является
наклонной асимптотой для графика
является
наклонной асимптотой для графика ![]() при
при ![]() .
.
Ответ: ![]()
Найдённые односторонние пределы и асимптоты с высокой достоверностью позволяют предположить, как выглядит график данной функции. Корректный чертёж в конце урока.
Пример 8
Найти
асимптоты графика функции
![]()
Это пример для самостоятельного решения, для удобства вычисления некоторых пределов можно почленно разделить числитель на знаменатель. И снова, анализируя полученные результаты, постарайтесь начертить график данной функции.
Очевидно,
что обладателями «настоящих» наклонных
асимптот являются графики тех
дробно-рациональных функций, у которых
старшая степень числителя на единицу
больше старшей степени знаменателя.
Если больше – наклонной асимптоты уже
не будет (например, ![]() ).
).
Но в жизни происходят и другие чудеса:
Пример 9
Исследовать
график функции на наличие асимптот
![]()
Решение:
функция непрерывна на
всей числовой прямой, значит, вертикальные
асимптоты отсутствует. Но вот наклонные
вполне могут быть. Проверяем:

Вспоминаю,
как ещё в ВУЗе столкнулся с похожей
функцией и просто не мог поверить, что
у неё есть наклонная асимптота. До тех
пор, пока не вычислил второй предел:
![]()
Строго
говоря, здесь две неопределённости: ![]() и
и ![]() ,
но так или иначе, нужно использовать
метод решения, который разобран в
Примерах 5-6 статьи о
пределах повышенной сложности.
Умножаем и делим на сопряженное выражение,
чтобы воспользоваться формулой
,
но так или иначе, нужно использовать
метод решения, который разобран в
Примерах 5-6 статьи о
пределах повышенной сложности.
Умножаем и делим на сопряженное выражение,
чтобы воспользоваться формулой ![]() :
:

Ответ: ![]()
Пожалуй, самая популярная наклонная асимптота.
До сих пор
бесконечности удавалось «стричь под
одну гребёнку», но бывает, что у графика
функции две разные наклонные
асимптоты при ![]() и
при
и
при ![]() :
:
Пример 10
Исследовать
график функции на наличие асимптот
![]()
Решение: подкоренное выражение положительно, значит, область определения – любое действительно число, и вертикальных палок быть не может.
Проверим, существуют ли наклонные асимптоты.
Если «икс»
стремится к «минус бесконечности»,
то:  (при
внесении «икса» под квадратный корень
необходимо добавить знак «минус», чтобы
не потерять отрицательность знаменателя)
(при
внесении «икса» под квадратный корень
необходимо добавить знак «минус», чтобы
не потерять отрицательность знаменателя)
![]()
Выглядит необычно, но здесь неопределённость «бесконечность минус бесконечность». Умножаем числитель и знаменатель на сопряженное выражение:

Таким
образом, прямая ![]() является
наклонной асимптотой графика при
является
наклонной асимптотой графика при ![]() .
.
С «плюс
бесконечностью» всё тривиальнее:

А прямая ![]() –
при
–
при ![]() .
.
Ответ:
![]() ,
если
,
если ![]() ;
;
![]() ,
если
,
если ![]() .
.
Не удержусь
от графического изображения:
 Это
одна из ветвей гиперболы
Это
одна из ветвей гиперболы ![]() .
.
Не редкость, когда потенциальное наличие асимптот изначально ограничено областью определения функции:
Пример 11
Исследовать
график функции на наличие асимптот
![]()
Решение:
очевидно, что ![]() ,
поэтому рассматриваем только правую
полуплоскость, где есть график функции.
,
поэтому рассматриваем только правую
полуплоскость, где есть график функции.
1)
Функция непрерывна на
интервале ![]() ,
а значит, если вертикальная асимптота
и существует, то это может быть только
ось ординат. Исследуем поведение функции
вблизи точки
,
а значит, если вертикальная асимптота
и существует, то это может быть только
ось ординат. Исследуем поведение функции
вблизи точки ![]() справа:
справа:
![]()
Обратите внимание, здесь НЕТ неопределённости (на таких случаях акцентировалось внимание в начале статьи Методы решения пределов).
Таким
образом, прямая ![]() (ось
ординат) является вертикальной асимптотой
для графика функции
(ось
ординат) является вертикальной асимптотой
для графика функции ![]() при
при ![]() .
.
2) Исследование
на наклонную асимптоту можно провести
по полной схеме, но в статьеПравила
Лопиталя мы выяснили, что линейная
функция более высокого порядка роста,
чем логарифмическая, следовательно: ![]() (см.
Пример 1 того же урока).
(см.
Пример 1 того же урока).
Вывод: ось
абсцисс является горизонтальной
асимптотой графика функции при ![]() .
.
Ответ:
![]() ,
если
,
если ![]() ;
;
![]() ,
если
,
если ![]() .
.
Чертёж для
наглядности:

Интересно,
что у вроде бы похожей функции ![]() асимптот
нет вообще (желающие могут это проверить).
асимптот
нет вообще (желающие могут это проверить).
Два заключительных примера для самостоятельного изучения:
Пример 12
Исследовать
график функции на наличие асимптот
![]()
Для проверки на вертикальные асимптоты сначала нужно найти область определения функции, а затем вычислить пару односторонних пределов в «подозрительных» точках. Наклонные асимптоты тоже не исключены, поскольку функция определена на «плюс» и «минус» бесконечности.
Интегралы от тригонометрических функций. Примеры решений
На данном уроке мы рассмотрим интегралы от тригонометрических функций, то есть начинкой интегралов у нас будут синусы, косинусы, тангенсы и котангенсы в различных комбинациях. Все примеры будут разобраны подробно, доступно и понятно даже для чайника.
Для успешного изучения интегралов от тригонометрических функций Вы должны хорошо ориентироваться в простейших интегралах, а также владеть некоторыми приемами интегрирования. Ознакомиться с этими материалами можно на лекциях Неопределенный интеграл. Примеры решений и Метод замены переменной в неопределенном интеграле. А сейчас нам потребуются: Таблица интегралов, Таблица производных и Справочник тригонометрических формул. Все методические пособия можно найти на страницеМатематические формулы и таблицы. Рекомендую всё распечатать. Особо заостряю внимание на тригонометрических формулах, они должны быть перед глазами – без этого эффективность работы заметно снизится.
Но сначала
о том, каких интегралов в данной
статье нет. Здесь не найдется
интегралов вида ![]() ,
, ![]() –
косинус, синус, умноженный на какой-нибудь
многочлен (реже что-нибудь с тангенсом
или котангенсом). Такие интегралы
интегрируются по частям, и для изучения
метода посетите урок Интегрирование
по частям. Примеры решений.Также
здесь не найдется интегралов с
«арками» – арктангенсом, арксинусом и
др., они тоже чаще всего интегрируются
по частям.
–
косинус, синус, умноженный на какой-нибудь
многочлен (реже что-нибудь с тангенсом
или котангенсом). Такие интегралы
интегрируются по частям, и для изучения
метода посетите урок Интегрирование
по частям. Примеры решений.Также
здесь не найдется интегралов с
«арками» – арктангенсом, арксинусом и
др., они тоже чаще всего интегрируются
по частям.
При нахождении интегралов от тригонометрических функций используется ряд методов:
Использование тригонометрических формул
Понижение степени подынтегральной функции (частный случай п.1)
Метод замены переменной
Универсальная тригонометрическая подстановка (частный случай п.3)
В рамках урока я постараюсь подробно разобрать все перечисленные методы и привести примеры решения типовых интегралов. Следует отметить, что данное разделение по параграфам весьма условно, поскольку очень часто вышеперечисленные правила используются одновременно.
Использование тригонометрических формул
Пример 1
Найти
неопределенный интеграл.
![]()
Сначала
полное решение, потом комментарии.
![]()
Используем
формулу:
![]()

(1) Мы видим,
что в подынтегральном выражении находится
произведение двух функций. К сожалению,
в интегральном исчислении нет удобной
формулы для интегрирования произведения: ![]() ,
поэтому приходится прибегать к различным
ухищрениям. В данном случае мы прерываем
решение значком
,
поэтому приходится прибегать к различным
ухищрениям. В данном случае мы прерываем
решение значком ![]() и
поясняем, что используется тригонометрическая
формула. Данная формула превращает
произведение в сумму.
и
поясняем, что используется тригонометрическая
формула. Данная формула превращает
произведение в сумму.
(2) Используем свойства линейности неопределенного интеграла – интеграл от суммы равен сумме интегралов; константу можно (и нужно) вынести за знак интеграла.
! Справка: При работе с тригонометрическими функциями следует помнить, что:
Косинус
– это четная функция, то есть ![]() ,
минус исчезает без всяких последствий.
В рассматриваемом примере:
,
минус исчезает без всяких последствий.
В рассматриваемом примере: ![]()
Синус –
функция нечетная: ![]() –
здесь минус, наоборот – не пропадает,
а выносится.
–
здесь минус, наоборот – не пропадает,
а выносится.
(3) Под
интегралами у нас сложные функции
(косинусы не просто от ![]() ,
а от сложного аргумента). Это простейшие
из сложных функций, интегралы от них
удобнее найти методом подведения под
знак дифференциала. Более подробно с
данным приёмом можно ознакомиться на
уроке Метод
замены переменной в неопределенном
интеграле.
(4) Используем табличную
формулу
,
а от сложного аргумента). Это простейшие
из сложных функций, интегралы от них
удобнее найти методом подведения под
знак дифференциала. Более подробно с
данным приёмом можно ознакомиться на
уроке Метод
замены переменной в неопределенном
интеграле.
(4) Используем табличную
формулу ![]() ,
единственное отличие, вместо «икса» у
нас сложное выражение.
,
единственное отличие, вместо «икса» у
нас сложное выражение.
Готово.
Пример 2
Найти
неопределенный интеграл.
![]()
Это пример для самостоятельного решения, полное решение и ответ – в конце урока.
Пример 3
Найти
неопределенный интеграл.
![]()
Классика жанра для тех, кто тонет на зачёте. Как Вы, наверное, заметили, в таблице интегралов нет интеграла от тангенса и котангенса, но, тем не менее, такие интегралы найти можно.
![]()
(1) Используем
тригонометрическую формулу ![]()
(2) Подводим функцию под знак дифференциала.
(3) Используем
табличный интеграл ![]() .
.
Пример 4
Найти
неопределенный интеграл.
![]()
Это пример для самостоятельного решения, полное решение и ответ – в конце урока.
Пример 5
Найти
неопределенный интеграл.
![]()
Степени у нас будут потихоньку повышаться =). Сначала решение:

(1) Используем
формулу ![]()
(2) Используем
основное тригонометрическое тождество ![]() ,
из которого следует, что
,
из которого следует, что ![]() .
.
(3) Почленно делим числитель на знаменатель.
(4) Используем свойство линейности неопределенного интеграла.
(5) Интегрируем с помощью таблицы.
Пример 6
Найти
неопределенный интеграл.
![]()
Это пример для самостоятельного решения, полное решение и ответ – в конце урока.
Также существуют интегралы от тангенсов и котангенсов, которые находятся в более высоких степенях. Интеграл от тангенса в кубе рассмотрен на уроке Как вычислить площадь плоской фигуры? Интегралы от тангенса (котангенса) в четвертой и пятой степенях можно раздобыть на странице Сложные интегралы.
Понижение степени подынтегральной функции
Данный
приём работает, когда подынтегральные
функции нафаршированы синусами и
косинусами в чётных степенях.
Для понижения степени используют
тригонометрические формулы ![]() ,
, ![]() и
и ![]() ,
причем последняя формула чаще используется
в обратном направлении:
,
причем последняя формула чаще используется
в обратном направлении: ![]() .
.
Пример 7
Найти
неопределенный интеграл.
![]()
Решение:
![]()
В принципе,
ничего нового здесь нет, за исключением
того, что мы применили формулу ![]() (понизив
степень подынтегральной функции).
Обратите внимание, что я сократил
решение. По мере накопления опыта
интеграл от
(понизив
степень подынтегральной функции).
Обратите внимание, что я сократил
решение. По мере накопления опыта
интеграл от ![]() можно
находить устно, это экономит время и
вполне допустимо при чистовом оформлении
заданий. В данном случае целесообразно
не расписывать и правило
можно
находить устно, это экономит время и
вполне допустимо при чистовом оформлении
заданий. В данном случае целесообразно
не расписывать и правило ![]() ,
сначала устно берем интеграл от 1, затем
– от
,
сначала устно берем интеграл от 1, затем
– от ![]() .
.
Пример 8
Найти
неопределенный интеграл.
![]()
Это пример для самостоятельного решения, полное решение и ответ – в конце урока.
Таки обещанное повышение степени:
Пример 9
Найти
неопределенный интеграл.
![]()
Сначала решение, потом комментарии:

(1) Готовим
подынтегральную функцию для применения
формулы ![]() .
.
(2) Собственно применяем формулу.
(3) Возводим знаменатель в квадрат и выносим константу за знак интеграла. Можно было поступить несколько иначе, но, на мой взгляд, так удобнее.
(4) Используем
формулу ![]()
(5) В третьем
слагаемом снова понижаем степень, но
уже с помощью формулы ![]() .
.
(6) Приводим
подобные слагаемые (здесь я почленно
разделил ![]() и
выполнил сложение
и
выполнил сложение ![]() ).
).
(7) Собственно
берём интеграл, правило линейности ![]() и
метод подведения функции под знак
дифференциала выполняем устно.
и
метод подведения функции под знак
дифференциала выполняем устно.
(8) Причесываем ответ.
! В неопределенном интеграле нередко ответ можно записать несколькими способами
В только
что рассмотренном примере окончательный
ответ ![]() можно
было записать иначе – раскрыть скобки
и даже это сделать еще до интегрирования
выражения, то есть вполне допустима
следующая концовка примера:
можно
было записать иначе – раскрыть скобки
и даже это сделать еще до интегрирования
выражения, то есть вполне допустима
следующая концовка примера:

Вполне возможно, что такой вариант даже удобнее, просто я объяснил так, как сам привык решать). Вот еще один характерный пример для самостоятельного решения:
Пример 10
Найти
неопределенный интеграл.
![]()
Это пример решается двумя способами, и у Вас могут получиться два совершенно разных ответа (точнее говоря, они будут выглядеть совершенно по-разному, а с математической точки зрения являться эквивалентными). Скорее всего, Вы не увидите наиболее рациональный способ и помучаетесь с раскрытием скобок, использованием других тригонометрических формул. Наиболее эффективное решение приведено в конце урока.
Подытоживая
параграф, сделаем вывод: любой интеграл
вида ![]() ,
где
,
где ![]() и
и ![]() – чётные числа,
решается методом понижения степени
подынтегральной функции.
На практике
мне встречались интегралы с 8 и 10
степенями, решать их ужасный
геморприходилось, понижая степень
несколько раз, в результате чего
получались длинные-длинные ответы.
– чётные числа,
решается методом понижения степени
подынтегральной функции.
На практике
мне встречались интегралы с 8 и 10
степенями, решать их ужасный
геморприходилось, понижая степень
несколько раз, в результате чего
получались длинные-длинные ответы.
Метод замены переменной
Как уже
упоминалось в статье Метод
замены переменной в неопределенном
интеграле, основной предпосылкой
для использования метода замены является
тот факт, что в подынтегральном выражении
есть некоторая функция ![]() и
её производная
и
её производная ![]() :
:
![]() (функции
(функции ![]() ,
, ![]() не
обязательно находятся в произведении)
не
обязательно находятся в произведении)
Пример 11
Найти
неопределенный интеграл.
![]()
Смотрим в
таблицу производных и замечаем
формулы ![]() ,
, ![]() ,
то есть, в нашем подынтегральном выражении
есть функция и её производная. Однако
мы видим, что при дифференцировании
косинус и синус взаимно превращаются
друг в друга, и возникает вопрос: как
выполнить замену переменной и что же
обозначать за
,
то есть, в нашем подынтегральном выражении
есть функция и её производная. Однако
мы видим, что при дифференцировании
косинус и синус взаимно превращаются
друг в друга, и возникает вопрос: как
выполнить замену переменной и что же
обозначать за ![]() –
синус или косинус?! Вопрос можно решить
методом научного тыка: если мы неправильно
выполним замену, то ничего хорошего не
получится.
–
синус или косинус?! Вопрос можно решить
методом научного тыка: если мы неправильно
выполним замену, то ничего хорошего не
получится.
Общий
ориентир: в похожих случаях за ![]() нужно
обозначить функцию, которая находится
в знаменателе.
нужно
обозначить функцию, которая находится
в знаменателе.
![]()
Прерываем
решение и проводим замену
![]()
 В
знаменателе у нас всё хорошо, всё зависит
только от
В
знаменателе у нас всё хорошо, всё зависит
только от ![]() ,
теперь осталось выяснить, во что
превратится
,
теперь осталось выяснить, во что
превратится ![]() .
Для
этого находим дифференциал
.
Для
этого находим дифференциал ![]() :
:
![]()
Или, если
короче: ![]() Из
полученного равенства по правилу
пропорции выражаем нужное нам выражение:
Из
полученного равенства по правилу
пропорции выражаем нужное нам выражение:
![]()
Итак:
 Теперь
всё подынтегральное выражение у нас
зависит только от
Теперь
всё подынтегральное выражение у нас
зависит только от ![]() и
можно продолжать решение
и
можно продолжать решение

Готово. Напоминаю, что цель замены – упростить подынтегральное выражение, в данном случае всё свелось к интегрированию степенной функции по таблице.
Я не случайно так подробно расписал этот пример, это сделано в целях повторения и закрепления материалов урока Метод замены переменной в неопределенном интеграле.
А сейчас два примера для самостоятельного решения:
Пример 12
Найти неопределенный интеграл.
![]()
Пример 13
Найти неопределенный интеграл.
![]()
Полные решения и ответы в конце урока.
Пример 14
Найти неопределенный интеграл.
![]()
Здесь опять
в подынтегральном выражении находятся
синус с косинусом (функция с производной),
но уже в произведении, и возникает
дилемма – что же обозначать за ![]() ,
синус или косинус?
,
синус или косинус?
Можно
попытаться провести замену методом
научного тыка, и, если ничего не получится,
то обозначить за ![]() другую
функцию, но есть:
другую
функцию, но есть:
Общий
ориентир: за ![]() нужно
обозначить ту функцию, которая, образно
говоря, находится в «неудобном положении».
нужно
обозначить ту функцию, которая, образно
говоря, находится в «неудобном положении».
Мы видим, что в данном примере студент косинус «мучается» от степени, а синус – свободно так сидит, сам по себе.
Поэтому
проведем замену:

Если у кого
остались трудности с алгоритмом замены
переменной и нахождением дифференциала ![]() ,
то следует вернуться к уроку Метод
замены переменной в неопределенном
интеграле.
,
то следует вернуться к уроку Метод
замены переменной в неопределенном
интеграле.
![]()
Пример 15
Найти неопределенный интеграл.
![]()
Анализируем
подынтегральную функцию, что нужно
обозначить за ![]() ?
Вспоминаем
наши ориентиры:
1) Функция, скорее
всего, находится в знаменателе;
2)
Функция находится в «неудобном положении».
?
Вспоминаем
наши ориентиры:
1) Функция, скорее
всего, находится в знаменателе;
2)
Функция находится в «неудобном положении».
Кстати, эти ориентиры справедливы не только для тригонометрических функций.
Под оба
критерия (особенно под второй) подходит
синус, поэтому напрашивается замена ![]() .
В принципе, замену можно уже проводить,
но сначала неплохо было бы разобраться,
а что делать с
.
В принципе, замену можно уже проводить,
но сначала неплохо было бы разобраться,
а что делать с ![]() ?
Во-первых, «отщипываем» один косинус:
?
Во-первых, «отщипываем» один косинус:
![]()
![]() мы
резервируем под наш «будущий»
дифференциал
мы
резервируем под наш «будущий»
дифференциал ![]()
А ![]() выражаем
через синус с помощью основного
тригонометрического тождества:
выражаем
через синус с помощью основного
тригонометрического тождества:
![]()
![]()
Вот теперь
замена: ![]()
![]()

Готово.
Общее
правило: Если в подынтегральной функции
одна из тригонометрических функций
(синус или косинус) находится
в нечетной степени, то
нужно от нечетной степени «откусить»
одну функцию, а за ![]() –
обозначить другую функцию. Речь
идет только об интегралах, где есть
косинусы и синусы.
–
обозначить другую функцию. Речь
идет только об интегралах, где есть
косинусы и синусы.
В рассмотренном
примере в нечетной степени у нас находился
косинус, поэтому мы отщипнули от степени
один косинус, а за ![]() обозначили
синус.
обозначили
синус.
Пример 16
Найти неопределенный интеграл.
![]()
Степени идут на взлёт =). Это пример для самостоятельного решения. Полное решение и ответ в конце урока.
Универсальная тригонометрическая подстановка
Универсальная
тригонометрическая подстановка – это
частый случай метода замены переменной.
Её можно попробовать применить, когда
«не знаешь, что делать». Но на самом деле
есть некоторые ориентиры для ее
применения. Типичными интегралами, где
нужно применить универсальную
тригонометрическую подстановку, являются
следующие интегралы:![]() ,
, ![]() ,
, ![]() ,
, ![]() и
т.д.
и
т.д.
Пример 17
Найти неопределенный интеграл.
![]()
Универсальная
тригонометрическая подстановка в данном
случае реализуется следующим способом.
Проведем замену: ![]() .
Я использую не букву
.
Я использую не букву ![]() ,
а букву
,
а букву ![]() ,
это не является каким-то правилом, просто
опять же я так привык решать.
,
это не является каким-то правилом, просто
опять же я так привык решать.
Здесь
удобнее находить дифференциал ![]() ,
для этого из равенства
,
для этого из равенства ![]() ,
я выражаю
,
я выражаю ![]() :
Навешиваю
на обе части арктангенс:
:
Навешиваю
на обе части арктангенс:
![]() Арктангенс
и тангенс взаимно уничтожаются:
Арктангенс
и тангенс взаимно уничтожаются:
![]()
![]()
Таким
образом:
![]()
На практике
можно не расписывать так подробно, а
просто пользоваться готовым результатом: ![]()
! Выражение ![]() справедливо
только в том случае, если под синусами
и косинусами у нас просто «иксы», для
интеграла
справедливо
только в том случае, если под синусами
и косинусами у нас просто «иксы», для
интеграла ![]() (о
котором мы еще поговорим) всё будет
несколько иначе!
(о
котором мы еще поговорим) всё будет
несколько иначе!
При
замене ![]() синусы
и косинусы у нас превращаются в следующие
дроби:
синусы
и косинусы у нас превращаются в следующие
дроби:
![]() ,
, ![]() ,
эти равенства основаны на известных
тригонометрических формулах:
,
эти равенства основаны на известных
тригонометрических формулах:  ,
, 
Итак, чистовое оформление может быть таким:
![]()
Проведем
универсальную тригонометрическую
подстановку: ![]()
![]()
![]()
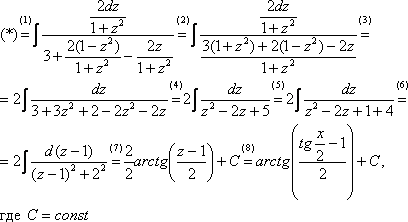
(1) Производим
в исходный интеграл подстановку: ![]() ,
, ![]() ,
, ![]() .
.
(2) Приводим знаменатель к общему знаменателю.
(3) Избавляемся
от четырехэтажности дроби, при этом ![]() у
нас сокращается. Раскрываем скобки в
знаменателе, двойку в числителе выносим
за знак интеграла.
у
нас сокращается. Раскрываем скобки в
знаменателе, двойку в числителе выносим
за знак интеграла.
(4) Приводим подобные слагаемые в знаменателе.
(5)
Интеграл ![]() решается методом
выделения полного квадрата. Более
подробно с этим методом можно ознакомиться
на уроке Интегрирование
некоторых дробей. Разложение
решается методом
выделения полного квадрата. Более
подробно с этим методом можно ознакомиться
на уроке Интегрирование
некоторых дробей. Разложение ![]() является
подготовкой для осуществления
вышеуказанного приёма
является
подготовкой для осуществления
вышеуказанного приёма
(6) Выделяем полный квадрат и готовим интеграл для интегрирования.
(7) Интегрируем
по табличной формуле ![]() .
.
(8) Проводим
обратную замену, вспоминая, что ![]() .
.
Готово.
Рассмотрим
похожий интеграл: ![]() ,
нет, решать мы его не будем =), а просто
поймем как проводить замену.
,
нет, решать мы его не будем =), а просто
поймем как проводить замену.
Здесь тоже
проводится универсальная тригонометрическая
подстановка: ![]() .
Обратите
внимание, что аргумент под тангенсом должен
быть в два раза меньше, чем под
синусом и косинусом. Формулы
.
Обратите
внимание, что аргумент под тангенсом должен
быть в два раза меньше, чем под
синусом и косинусом. Формулы ![]() ,
, ![]() сохраняют
статус-кво, а вот дифференциал будет
немного другой (я не зря недавно так
подробно его расписал):
сохраняют
статус-кво, а вот дифференциал будет
немного другой (я не зря недавно так
подробно его расписал):
![]()
![]()
Интеграл ![]() решается
путем замены
решается
путем замены ![]() и
т.д., всё точно так же, единственное
отличие, дифференциал будет опять
немного другой.
и
т.д., всё точно так же, единственное
отличие, дифференциал будет опять
немного другой.
Интегрирование по частям. Примеры решений
И снова, здравствуйте. Сегодня на уроке мы научимся интегрировать по частям. Метод интегрирования по частям – это один из краеугольных камней интегрального исчисления. На зачете, экзамене студенту почти всегда предлагают решить интегралы следующих типов: простейший интеграл (см. статью Неопределенный интеграл. Примеры решений) либо интеграл на замену переменной (см. статью Метод замены переменной в неопределенном интеграле) либо интеграл как раз на метод интегрирования по частям.
Для эффективного изучения темы необходимо хорошо ориентироваться в материалах двух вышеуказанных уроков. Если Вы чайник, и только-только начинаете погружение в удивительный мир интегралов, то читать далее не имеет особого смысла – следует начать с урока Неопределенный интеграл. Примеры решений.
Как всегда, под рукой должны быть: Таблица интегралов и Таблица производных. Если у Вас до сих пор их нет, то, пожалуйста, посетите кладовку моего сайта: Математические формулы и таблицы. Не устану повторять – лучше всё распечатать. Весь материал я постараюсь изложить последовательно, просто и доступно, в интегрировании по частям нет особых трудностей.
Какую задачу
решает метод интегрирования по частям?
Метод интегрирования по частям решает
очень важную задачу, он позволяет
интегрировать некоторые функции,
отсутствующие в таблице, произведение функций,
а в ряде случаев – и частное. Как мы
помним, нет удобной формулы:![]() .
Зато есть такая:
.
Зато есть такая: ![]() –
формула интегрирования по частям
собственной персоной. Знаю, знаю, ты
одна такая – с ней мы и будем работать
весь урок (уже легче).
–
формула интегрирования по частям
собственной персоной. Знаю, знаю, ты
одна такая – с ней мы и будем работать
весь урок (уже легче).
И сразу список в студию. По частям берутся интегралы следующих видов:
1) ![]() ,
, ![]() ,
, ![]() –
логарифм, логарифм, умноженный на
какой-нибудь многочлен.
–
логарифм, логарифм, умноженный на
какой-нибудь многочлен.
2) ![]() ,
,![]() –
экспоненциальная функция, умноженная
на какой-нибудь многочлен. Сюда же можно
отнести интегралы вроде
–
экспоненциальная функция, умноженная
на какой-нибудь многочлен. Сюда же можно
отнести интегралы вроде ![]() –
показательная функция, умноженная на
многочлен, но на практике процентах так
в 97, под интегралом красуется симпатичная
буква «е». … что-то лирической получается
статья, ах да… весна же пришла.
–
показательная функция, умноженная на
многочлен, но на практике процентах так
в 97, под интегралом красуется симпатичная
буква «е». … что-то лирической получается
статья, ах да… весна же пришла.
3) ![]() ,
, ![]() ,
, ![]() –
тригонометрические функции, умноженные
на какой-нибудь многочлен.
–
тригонометрические функции, умноженные
на какой-нибудь многочлен.
4) ![]() ,
, ![]() –
обратные тригонометрические функции
(«арки»), «арки», умноженные на какой-нибудь
многочлен.
–
обратные тригонометрические функции
(«арки»), «арки», умноженные на какой-нибудь
многочлен.
Также по частям берутся некоторые дроби, соответствующие примеры мы тоже подробно рассмотрим.
Интегралы от логарифмов
Пример 1
Найти неопределенный интеграл.
![]()
Классика. Время от времени данный интеграл можно встретить в таблицах, но пользоваться готовым ответом нежелательно, так как у преподавателя весенний авитаминоз и он сильно заругается. Потому что рассматриваемый интеграл отнюдь не табличный – он берётся по частям. Решаем:
![]()
Прерываем решение на промежуточные объяснения.
Используем
формулу интегрирования по частям: ![]()
Формула применяется слева направо
Смотрим на
левую часть: ![]() .
Очевидно, что в нашем примере
.
Очевидно, что в нашем примере ![]() (и
во всех остальных, которые мы рассмотрим)
что-то нужно обозначить за
(и
во всех остальных, которые мы рассмотрим)
что-то нужно обозначить за ![]() ,
а что-то за
,
а что-то за ![]() .
.
В интегралах
рассматриваемого типа за ![]() всегда
обозначается логарифм.
всегда
обозначается логарифм.
Технически оформление решения реализуется следующим образом, в столбик записываем:
![]()
То есть,
за ![]() мы
обозначили логарифм, а за
мы
обозначили логарифм, а за ![]() – оставшуюся
часть подынтегрального выражения.
– оставшуюся
часть подынтегрального выражения.
Следующий
этап: находим дифференциал ![]() :
:

Дифференциал – это почти то же самое, что и производная, как его находить, мы уже разбирали на предыдущих уроках.
Теперь
находим функцию ![]() .
Для того чтобы найти функцию
.
Для того чтобы найти функцию ![]() необходимо
проинтегрироватьправую часть нижнего
равенства
необходимо
проинтегрироватьправую часть нижнего
равенства ![]() :
:

Теперь
открываем наше решение и конструируем
правую часть формулы: ![]() .
Вот
кстати, и образец чистового решения с
небольшими пометками:
.
Вот
кстати, и образец чистового решения с
небольшими пометками:
 Единственный
момент, в произведении
Единственный
момент, в произведении ![]() я
сразу переставил местами
я
сразу переставил местами ![]() и
и ![]() ,
так как множитель
,
так как множитель ![]() принято
записывать перед логарифмом.
принято
записывать перед логарифмом.
Как видите, применение формулы интегрирования по частям, по сути дела, свело наше решение к двум простым интегралам.
Обратите внимание, что в ряде случаев сразу после применения формулы, под оставшимся интегралом обязательно проводится упрощение – в рассматриваемом примере мы сократили подынтегральное выражение на «икс».
Выполним проверку. Для этого нужно взять производную от ответа:

Получена исходная подынтегральная функция, значит, интеграл решён правильно.
В ходе
проверки мы использовали правило
дифференцирования произведения: ![]() .
И это не случайно.
.
И это не случайно.
Формула
интегрирования по частям ![]() и
формула
и
формула ![]() –
это два взаимно обратных правила.
–
это два взаимно обратных правила.
Пример 2
Найти неопределенный интеграл.
![]()
Подынтегральная функция представляет собой произведение логарифма на многочлен. Решаем.
![]()
Я еще один раз подробно распишу порядок применения правила, в дальнейшем примеры будут оформляться более кратко, и, если у Вас возникнут трудности в самостоятельном решении, нужно вернуться обратно к первым двум примерам урока.
Как уже
говорилось, за ![]() необходимо
обозначить логарифм (то, что он в
степени – значения не имеет).
За
необходимо
обозначить логарифм (то, что он в
степени – значения не имеет).
За ![]() обозначаем оставшуюся
часть подынтегрального выражения.
обозначаем оставшуюся
часть подынтегрального выражения.
Записываем
в столбик:
![]()
Сначала
находим дифференциал ![]() :
:

Здесь
использовано правило дифференцирования
сложной функции ![]() .
Не случайно, на самом первом уроке
темы Неопределенный
интеграл. Примеры решений я
акцентировал внимание на том, что для
того, чтобы освоить интегралы, необходимо
«набить руку» на производных. С
производными придется столкнуться еще
не раз.
.
Не случайно, на самом первом уроке
темы Неопределенный
интеграл. Примеры решений я
акцентировал внимание на том, что для
того, чтобы освоить интегралы, необходимо
«набить руку» на производных. С
производными придется столкнуться еще
не раз.
Теперь
находим функцию ![]() ,
для этого интегрируем правую
часть нижнего равенства
,
для этого интегрируем правую
часть нижнего равенства ![]() :
:

Для
интегрирования мы применили простейшую
табличную формулу ![]()
Теперь всё
готово для применения формулы ![]() .
Открываем «звёздочкой» и «конструируем»
решение в соответствии с правой частью
.
Открываем «звёздочкой» и «конструируем»
решение в соответствии с правой частью ![]() :
:

Под интегралом
у нас снова многочлен на логарифм!
Поэтому решение опять прерывается и
правило интегрирования по частям
применяется второй раз. Не забываем,
что за ![]() в
похожих ситуациях всегда обозначается
логарифм.
в
похожих ситуациях всегда обозначается
логарифм.

Хорошо бы, если к данному моменту простейшие интегралы и производные Вы умели находить устно.

(1) Не
путаемся в знаках! Очень часто здесь
теряют минус, также обратите внимание,
что минус относится ко
всей скобке  ,
и эти скобки нужно корректно раскрыть.
,
и эти скобки нужно корректно раскрыть.
(2) Раскрываем скобки. Последний интеграл упрощаем.
(3) Берем последний интеграл.
(4) «Причесываем» ответ.
Необходимость дважды (а то и трижды) применять правило интегрирования по частям возникает не так уж и редко.
А сейчас пара примеров для самостоятельного решения:
Пример 3
Найти неопределенный интеграл.
![]()
Этот пример решается методом замены переменной (или подведением под знак дифференциала)! А почему бы и нет – можете попробовать взять его по частям, получится забавная вещь.
Пример 4
Найти неопределенный интеграл.
![]()
А вот этот интеграл интегрируется по частям (обещанная дробь).
Это примеры для самостоятельного решения, решения и ответы в конце урока.
Вроде бы в примерах 3,4 подынтегральные функции похожи, а вот методы решения – разные! В этом-то и состоит основная трудность освоения интегралов – если неправильно подобрать метод решения интеграла, то возиться с ним можно часами, как с самой настоящей головоломкой. Поэтому чем больше вы прорешаете различных интегралов – тем лучше, тем легче пройдут зачет и экзамен. Кроме того, на втором курсе будут дифференциальные уравнения, а без опыта решения интегралов и производных делать там нечего.
По логарифмам, пожалуй, более чем достаточно. На закуску могу еще вспомнить, что студенты-технари логарифмами называют женскую грудь =). Кстати, полезно знать назубок графики основных элементарных функций: синуса, косинуса, арктангенса, экспоненты, многочленов третьей, четвертой степени и т.д. Нет, конечно, презерватив на глобус я натягивать не буду, но теперь вы многое запомните из раздела Графики и функции =).
Интегралы от экспоненты, умноженной на многочлен
Общее
правило: за ![]() всегда
обозначается многочлен
всегда
обозначается многочлен
Пример 5
Найти неопределенный интеграл.
![]()
Решение:
![]()
Используя знакомый алгоритм, интегрируем по частям:
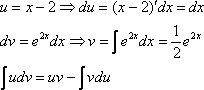

Если возникли
трудности с интегралом ![]() ,
то следует вернуться к статье Метод
замены переменной в неопределенном
интеграле.
,
то следует вернуться к статье Метод
замены переменной в неопределенном
интеграле.
Единственное, что еще можно сделать, это «причесать» ответ:

Но если
Ваша техника вычислений не очень хороша,
то самый выгодный вариант оставить
ответом ![]() или
даже
или
даже ![]()
То есть, пример считается решенным, когда взят последний интеграл. Ошибкой не будет, другое дело, что преподаватель может попросить упростить ответ.
Пример 6
Найти неопределенный интеграл.
![]()
Это пример
для самостоятельного решения. Данный
интеграл дважды интегрируется по частям.
Особое внимание следует обратить на
знаки – здесь легко в них запутаться,
также помним, что ![]() –
сложная функция.
–
сложная функция.
Больше про экспоненту рассказывать особо нечего. Могу только добавить, что экспонента и натуральный логарифм взаимно-обратные функции, это я к теме занимательных графиков высшей математики =) Стоп-стоп, не волнуемся, лектор трезв.
Интегралы от тригонометрических функций, умноженных на многочлен
Общее
правило: за ![]() всегда
обозначается многочлен
всегда
обозначается многочлен
Пример 7
Найти неопределенный интеграл.
![]()
Интегрируем по частям:


Хммм, …и комментировать нечего.
Пример 8
Найти
неопределенный интеграл
![]()
Это пример для самостоятельного решения
Пример 9
Найти
неопределенный интеграл
![]()
Еще один
пример с дробью. Как и в двух предыдущих
примерах за ![]() обозначается
многочлен.
обозначается
многочлен.
![]()
Интегрируем
по частям:

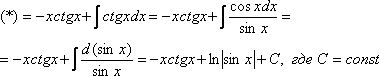
Если возникли
трудности или недопонимание с нахождением
интеграла ![]() ,
то рекомендую посетить урок Интегралы
от тригонометрических функций.
,
то рекомендую посетить урок Интегралы
от тригонометрических функций.
Пример 10
Найти
неопределенный интеграл
![]()
Это пример для самостоятельного решения.
Подсказка: перед использованием метода интегрирования по частям следует применить некоторую тригонометрическую формулу, которая превращает произведение двух тригонометрических функций в одну функцию. Формулу также можно использовать и в ходе применения метода интегрирования по частям, кому как удобнее.
Вот, пожалуй, и всё в данном параграфе. Почему-то вспомнилась строчка из гимна физмата «А синуса график волна за волной по оси абсцисс пробегает»….
Интегралы от обратных тригонометрических функций. Интегралы от обратных тригонометрических функций, умноженных на многочлен
Общее
правило: за ![]() всегда
обозначается обратная тригонометрическая
функция.
всегда
обозначается обратная тригонометрическая
функция.
Напоминаю, что к обратным тригонометрическим функциям относятся арксинус, арккосинус, арктангенс и арккотангенс. Для краткости записи я буду называть их «арками»
Пример 11
Найти
неопределенный интеграл.
![]()
Решаем.
![]()
Интегрируем
по частям:


Интеграл ![]() найден
методом подведения функции под знак
дифференциала, можно использовать и
метод замены в «классическом» виде.
Аналогичный пример мы разбирали на
уроке Метод замены переменной в
неопределенном интеграле.
найден
методом подведения функции под знак
дифференциала, можно использовать и
метод замены в «классическом» виде.
Аналогичный пример мы разбирали на
уроке Метод замены переменной в
неопределенном интеграле.
Таким образом, помимо «чистого» интегрирования по частям нередко требуется применять и другие методы, приёмы решения.
Интегрирование дробно-рациональной функции. Метод неопределенных коэффициентов
Продолжаем заниматься интегрированием дробей. Интегралы от некоторых видов дробей мы уже рассмотрели на уроке Интегрирование некоторых дробей, и этот урок в некотором смысле можно считать продолжением. Для успешного понимания материала необходимы базовые навыки интегрирования, поэтому если Вы только приступили к изучению интегралов, то есть, являетесь чайником, то необходимо начать со статьи Неопределенный интеграл. Примеры решений.
Как ни странно, сейчас мы будем заниматься не столько нахождением интегралов, сколько… решением систем линейных уравнений. В этой связи настоятельно рекомендую посетить урокКак решить систему линейных уравнений? А именно – нужно хорошо ориентироваться в методах подстановке («школьном» методе) и методе почленного сложения (вычитания) уравнений системы.
Что такое дробно-рациональная функция? Простыми словами, дробно-рациональная функция – это дробь, в числителе и знаменателе которой находятся многочлены либо произведения многочленов. При этом дроби является более навороченными, нежели те, о которых шла речь в статье Интегрирование некоторых дробей.
Интегрирование правильной дробно-рациональной функции
Сразу пример и типовой алгоритм решения интеграла от дробно-рациональной функции.
Пример 1
Найти
неопределенный интеграл.
![]()
Шаг 1. Первое, что мы ВСЕГДА делаем при решении интеграла от дробно-рациональной функции – это выясняем следующий вопрос: является ли дробь правильной? Данный шаг выполняется устно, и сейчас я объясню как:
Сначала
смотрим на числитель и выясняем старшую
степень многочлена:
 Старшая
степень числителя равна двум.
Старшая
степень числителя равна двум.
Теперь
смотрим на знаменатель и выясняем старшую
степень знаменателя. Напрашивающийся
путь – это раскрыть скобки и привести
подобные слагаемые, но можно поступить
проще, в каждой скобке находим
старшую степень
 и
мысленно умножаем:
и
мысленно умножаем: ![]() –
таким образом, старшая степень знаменателя
равна трём. Совершенно очевидно, что
если реально раскрыть скобки, то мы не
получим степени, больше трёх.
–
таким образом, старшая степень знаменателя
равна трём. Совершенно очевидно, что
если реально раскрыть скобки, то мы не
получим степени, больше трёх.
Вывод: Старшая степень числителя СТРОГО меньше старшей степени знаменателя, значит, дробь является правильной.
Если бы в данном примере в числителе находился многочлен 3, 4, 5 и т.д. степени, то дробь была бы неправильной.
Сейчас мы будем рассматривать только правильные дробно-рациональные функции. Случай, когда степень числителя больше либо равна степени знаменателя, разберём в конце урока.
Шаг
2. Разложим знаменатель на множители.
Смотрим на наш знаменатель:
![]() Вообще
говоря, здесь уже произведение множителей,
но, тем не менее, задаемся вопросом:
нельзя ли что-нибудь разложить еще?
Объектом пыток, несомненно, выступит
квадратный трехчлен. Решаем квадратное
уравнение:
Вообще
говоря, здесь уже произведение множителей,
но, тем не менее, задаемся вопросом:
нельзя ли что-нибудь разложить еще?
Объектом пыток, несомненно, выступит
квадратный трехчлен. Решаем квадратное
уравнение:
![]()
Дискриминант больше нуля, значит, трехчлен действительно раскладывается на множители:

Общее правило: ВСЁ, что в знаменателе МОЖНО разложить на множители – раскладываем на множители.
Начинаем оформлять решение:
![]()
Шаг 3. Методом неопределенных коэффициентов раскладываем подынтегральную функцию в сумму простых (элементарных) дробей. Сейчас будет понятнее.
Смотрим на
нашу подынтегральную функцию:
![]()
И, знаете,
как-то проскакивает интуитивная мысль,
что неплохо бы нашу большую дробь
превратить в несколько маленьких.
Например, вот так:
![]()
Возникает вопрос, а можно ли вообще так сделать? Вздохнем с облегчением, соответствующая теорема математического анализа утверждает – МОЖНО. Такое разложение существует и единственно.
Только есть
одна загвоздочка, коэффициенты ![]() мы пока не
знаем, отсюда и название – метод
неопределенных коэффициентов.
мы пока не
знаем, отсюда и название – метод
неопределенных коэффициентов.
Как вы
догадались, последующие телодвижения так,
не гоготать! будут направлены на то,
чтобы как раз их УЗНАТЬ – выяснить,
чему же равны ![]() .
.
Будьте внимательны, подробно объясняю один раз!
Итак,
начинаем плясать от:
![]()
В левой
части приводим выражение к общему
знаменателю:
![]()
Теперь
благополучно избавляемся от знаменателей
(т.к. они одинаковы):
![]()
В левой
части раскрываем скобки, неизвестные
коэффициенты ![]() при
этом пока не трогаем:
при
этом пока не трогаем:
![]()
Заодно повторяем школьное правило умножение многочленов. В свою бытность учителем, я научился выговаривать это правило с каменным лицом: Для того чтобы умножить многочлен на многочлен нужно каждый член одного многочлена умножить на каждый член другого многочлена.
С точки
зрения понятного объяснения
коэффициенты ![]() лучше
внести в скобки (хотя лично я никогда
этого не делаю в целях экономии времени):
лучше
внести в скобки (хотя лично я никогда
этого не делаю в целях экономии времени):
![]()
Составляем
систему линейных уравнений.
Сначала
разыскиваем старшие степени:
 И
записываем соответствующие коэффициенты
в первое уравнение системы:
И
записываем соответствующие коэффициенты
в первое уравнение системы:

Хорошо
запомните следующий нюанс. Что
было бы, если б в правой части вообще не
было ![]() ?
Скажем, красовалось бы просто
?
Скажем, красовалось бы просто ![]() без
всякого квадрата? В этом случае в
уравнении системы нужно было бы поставить
справа ноль:
без
всякого квадрата? В этом случае в
уравнении системы нужно было бы поставить
справа ноль: ![]() .
Почему ноль? А потому-что в правой части
всегда можно приписать этот самый
квадрат с нулём:
.
Почему ноль? А потому-что в правой части
всегда можно приписать этот самый
квадрат с нулём: ![]() . Если
в правой части отсутствует какие-нибудь
переменные или (и) свободный член, то в
правых частях соответствующих уравнений
системы ставим нули.
. Если
в правой части отсутствует какие-нибудь
переменные или (и) свободный член, то в
правых частях соответствующих уравнений
системы ставим нули.
Далее
процесс идет по снижающейся траектории,
от водки к пиву, отмечаем все «иксы»:
![]()
Записываем
соответствующие коэффициенты во второе
уравнение системы:
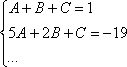
И, наконец, минералка, подбираем свободные члены.
Эх,…что-то я расшутился. Шутки прочь – математика наука серьезная. У нас в институтской группе никто не смеялся, когда доцент на лекции сказала, что разбросает члены по координатной прямой и выберет из них самые большие. Настраиваемся на серьезный лад. Хотя… кто доживет до конца этого урока, все равно будет тихо улыбаться.
![]()
Система готова:

Решаем
систему:

(1) Из первого
уравнения выражаем ![]() и
подставляем его во 2-ое и 3-е уравнения
системы. На самом деле можно было
выразить
и
подставляем его во 2-ое и 3-е уравнения
системы. На самом деле можно было
выразить ![]() (или
другую букву) из другого уравнения, но
в данном случае выгодно выразить именно
из 1-го уравнения, поскольку там самые
маленькие коэффициенты.
(2)
Приводим подобные слагаемые во 2-ом и
3-м уравнениях.
(или
другую букву) из другого уравнения, но
в данном случае выгодно выразить именно
из 1-го уравнения, поскольку там самые
маленькие коэффициенты.
(2)
Приводим подобные слагаемые во 2-ом и
3-м уравнениях.
(3) Почленно
складываем 2-ое и 3-е уравнение, при этом,
получая равенство ![]() ,
из которого следует, что
,
из которого следует, что ![]()
(4)
Подставляем ![]() во
второе (или третье) уравнение, откуда
находим, что
во
второе (или третье) уравнение, откуда
находим, что ![]()
(5)
Подставляем ![]() и
и ![]() в
первое уравнение, получая
в
первое уравнение, получая ![]() .
.
Если возникли трудности с методами решения системы отработайте их на уроке Как решить систему линейных уравнений?
После
решения системы всегда полезно сделать
проверку – подставить найденные
значения ![]() в
каждое уравнение системы, в
результате всё должно «сойтись».
в
каждое уравнение системы, в
результате всё должно «сойтись».
Почти
приехали. Коэффициенты ![]() найдены,
при этом:
найдены,
при этом:
![]()
Чистовое оформление задание должно выглядеть примерно так:
![]()
Методом неопределенных коэффициентов разложим подынтегральную функцию в сумму элементарных дробей:
![]()
![]()
![]()


Как видите, основная трудность задания состояла в том, чтобы составить (правильно!) и решить (правильно!) систему линейных уравнений. А на завершающем этапе всё не так сложно: используем свойства линейности неопределенного интеграла и интегрируем. Обращаю внимание, что под каждым из трёх интегралов у нас «халявная» сложная функция, об особенностях ее интегрирования я рассказал на уроке Метод замены переменной в неопределенном интеграле.
Проверка: Дифференцируем ответ:

Получена исходная подынтегральная функция, значит, интеграл найден правильно. В ходе проверки пришлось приводить выражение к общему знаменателю, и это не случайно.Метод неопределенных коэффициентов и приведение выражения к общему знаменателю – это взаимно обратные действия.
Пример 2
Найти
неопределенный интеграл.
![]()
Это пример для самостоятельного решения. Полное решение и ответ в конце урока.
Вернемся
к дроби из первого примера: ![]() .
Нетрудно заметить, что в знаменателе
все множители РАЗНЫЕ. Возникает вопрос,
а что делать, если дана, например, такая
дробь:
.
Нетрудно заметить, что в знаменателе
все множители РАЗНЫЕ. Возникает вопрос,
а что делать, если дана, например, такая
дробь: ![]() ?
Здесь в знаменателе у нас степени, или,
по-математически кратные множители.
Кроме того, есть неразложимый на множители
квадратный трехчлен
?
Здесь в знаменателе у нас степени, или,
по-математически кратные множители.
Кроме того, есть неразложимый на множители
квадратный трехчлен ![]() (легко
убедиться, что дискриминант
уравнения
(легко
убедиться, что дискриминант
уравнения ![]() отрицателен,
поэтому на множители трехчлен никак не
разложить). Что делать? Разложение в
сумму элементарных дробей будет выглядеть
наподобие
отрицателен,
поэтому на множители трехчлен никак не
разложить). Что делать? Разложение в
сумму элементарных дробей будет выглядеть
наподобие ![]() с
неизвестными коэффициентами
с
неизвестными коэффициентами ![]() вверху
или как-то по-другому?
вверху
или как-то по-другому?
Пример 3
Представить
функцию ![]() в
виде суммы элементарных дробей с
неизвестными коэффициентами.
в
виде суммы элементарных дробей с
неизвестными коэффициентами.
Шаг
1. Проверяем, правильная ли у нас
дробь
Старшая степень числителя:
2
Старшая степень знаменателя: 8
![]() ,
значит, дробь является правильной.
,
значит, дробь является правильной.
Шаг
2. Можно ли что-нибудь разложить в
знаменателе на множители? Очевидно, что
нет, всё уже разложено. Квадратный
трехчлен ![]() не
раскладывается в произведение по
указанным выше причинам. Гуд. Работы
меньше.
не
раскладывается в произведение по
указанным выше причинам. Гуд. Работы
меньше.
Шаг 3. Представим дробно-рациональную функцию в виде суммы элементарных дробей. В данном случае, разложение имеет следующий вид:
![]()
Смотрим на
наш знаменатель: ![]() При
разложении дробно-рациональной функции
в сумму элементарных дробей можно
выделить три принципиальных момента:
При
разложении дробно-рациональной функции
в сумму элементарных дробей можно
выделить три принципиальных момента:
1) Если в
знаменателе находится «одинокий»
множитель в первой степени (в нашем
случае ![]() ),
то вверху ставим неопределенный
коэффициент (в нашем случае
),
то вверху ставим неопределенный
коэффициент (в нашем случае ![]() ).
Примеры №1,2 состояли только из таких
«одиноких» множителей.
).
Примеры №1,2 состояли только из таких
«одиноких» множителей.
2) Если в
знаменателе есть кратный множитель ![]() ,
то раскладывать нужно так:
,
то раскладывать нужно так:
![]() –
то есть последовательно перебрать все
степени «икса» от первой до энной
степени. В нашем примере два кратных
множителя:
–
то есть последовательно перебрать все
степени «икса» от первой до энной
степени. В нашем примере два кратных
множителя: ![]() и
и ![]() ,
еще раз взгляните на приведенное мной
разложение и убедитесь, что они разложены
именно по этому правилу.
,
еще раз взгляните на приведенное мной
разложение и убедитесь, что они разложены
именно по этому правилу.
3) Если в
знаменателе находится неразложимый
многочлен второй степени (в нашем
случае ![]() ),
то при разложении в числителе нужно
записать линейную функцию с неопределенными
коэффициентами (в нашем случае
),
то при разложении в числителе нужно
записать линейную функцию с неопределенными
коэффициентами (в нашем случае ![]() с
неопределенными коэффициентами
с
неопределенными коэффициентами ![]() и
и ![]() ).
).
На самом деле, есть еще 4-ый случай, но о нём я умолчу, поскольку на практике он встречается крайне редко.
Пример 4
Представить
функцию ![]() в
виде суммы элементарных дробей с
неизвестными коэффициентами.
в
виде суммы элементарных дробей с
неизвестными коэффициентами.
Это пример для самостоятельного решения. Полное решение и ответ в конце урока. Строго следуйте алгоритму!
Если Вы разобрались, по каким принципам нужно раскладывать дробно-рациональную функцию в сумму, то сможете разгрызть практически любой интеграл рассматриваемого типа.
Пример 5
Найти
неопределенный интеграл.
![]()
Шаг
1. Очевидно, что дробь является
правильной: ![]()
Шаг
2. Можно ли что-нибудь разложить в
знаменателе на множители? Можно. Здесь
сумма кубов ![]() .
Раскладываем знаменатель на множители,
используя формулу сокращенного
умножения
.
Раскладываем знаменатель на множители,
используя формулу сокращенного
умножения ![]()
![]()
Шаг 3. Методом неопределенных коэффициентов разложим подынтегральную функцию в сумму элементарных дробей:
![]()
Обратите
внимание, что многочлен ![]() неразложим
на множители (проверьте, что дискриминант
отрицательный), поэтому вверху мы ставим
линейную функцию
неразложим
на множители (проверьте, что дискриминант
отрицательный), поэтому вверху мы ставим
линейную функцию ![]() с
неизвестными коэффициентами, а не просто
одну буковку.
с
неизвестными коэффициентами, а не просто
одну буковку.
Приводим
дробь к общему знаменателю:
![]()
![]()
Составим и решим систему:

(1) Из первого
уравнения выражаем ![]() и
подставляем во второе уравнение системы
(это наиболее рациональный способ).
и
подставляем во второе уравнение системы
(это наиболее рациональный способ).
(2) Приводим подобные слагаемые во втором уравнении.
(3) Почленно складываем второе и третье уравнения системы.
Все дальнейшие
расчеты, в принципе, устные, так как
система несложная.

(1) Записываем
сумму дробей в соответствии с найденными
коэффициентами ![]() .
.
(2) Используем свойства линейности неопределенного интеграла. Что произошло во втором интеграле? С этим методом Вы можете ознакомиться в последнем параграфе урокаИнтегрирование некоторых дробей.
(3) Еще раз используем свойства линейности. В третьем интеграле начинаем выделять полный квадрат (предпоследний параграф урока Интегрирование некоторых дробей).
(4) Берём второй интеграл, в третьем – выделяем полный квадрат.
(5) Берём третий интеграл. Готово.
А вот вам еще пара примеров для самостоятельного решения, один похожий, другой – труднее.
Пример 6
Найти
неопределенный интеграл.
![]()
Пример 7
Найти
неопределенный интеграл.
![]()
Интегрирование неправильной дробно-рациональной функции
Перейдем к рассмотрению случая, когда старшая степень числителя больше либо равна старшей степени знаменателя.
Пример 8
Найти неопределенный интеграл.
![]()
Совершенно
очевидно, что данная дробь является
неправильной: ![]()
Основной метод решения интеграла с неправильной дробно-рациональной функций – этоделение числителя на знаменатель. Алгоритм деления многочленов столбиком рассматривался на уроке Сложные пределы, и сейчас мы закрепим навыки.
Сначала
рисуем «заготовку» для деления:

ВСЕ недостающие степени (и (или) свободные члены) без пропусков записываем в ОБОИХ многочленах с нулевыми коэффициентами.
Теперь
маленькая задачка, на какой множитель
нужно умножить ![]() ,
чтобы получить
,
чтобы получить ![]() ?
Очевидно, что на
?
Очевидно, что на ![]() :
:

Далее
умножаем ![]() сначала
на
сначала
на ![]() ,
потом – на
,
потом – на ![]() ,
потом – на
,
потом – на ![]() ,
потом – на 0 и записываем результаты
слева:
,
потом – на 0 и записываем результаты
слева:

Проводим
черточку и производим вычитание (из
верха вычитаем низ):
 Старшая
степень остатка
Старшая
степень остатка ![]() равна
двум, старшая степень делителя
равна
двум, старшая степень делителя ![]() –
больше, она равна трём, значит, больше
разделить не удастся. Если бы изначально
у нас был в числителе многочлен пятой
степени, то то алгоритм деления увеличился
бы на один шаг.
–
больше, она равна трём, значит, больше
разделить не удастся. Если бы изначально
у нас был в числителе многочлен пятой
степени, то то алгоритм деления увеличился
бы на один шаг.
Итак, наше
решение принимает следующий вид:
![]()
Делим
числитель на знаменатель:


(1) Что дало деление? Много хорошего: теперь у нас два слагаемых, первое – интегрируется совсем просто, а второе – правильная дробь, которую мы решать уже умеем.
После
деления всегда желательно выполнять
проверку.
В рассматриваемом примере
можно привести к общему знаменателю ![]() ,
и в результате получится в точности
исходная неправильная дробь
,
и в результате получится в точности
исходная неправильная дробь ![]()
(2) От первого слагаемого сразу берем интеграл. Знаменатель дроби раскладываем на множители
Дальше всё идет по накатанной схеме:
Методом
неопределенных коэффициентов разложим
подынтегральную функцию в сумму
элементарных дробей:
![]()


![]()
Интегрирование корней (иррациональных функций). Примеры решений
Вот и пробил час интегралов от корней, они вас заждались! С моей точки зрения интегрирование иррациональных функций следует изучать уже при некоторых знаниях и навыках решения неопределенного интеграла, поскольку интегралы от корней, во-первых, встречаются реже, чем другие типы интегралов, а во-вторых, некоторые из них – самые настоящие крепкие орешки. Таким образом, если Вы чайник, и за плечами всего десяток прорешанных интегралов, да и с методом замены переменной в неопределенном интеграле не очень, то лучше начать со статьи Неопределенный интеграл. Примеры решений. Хотя, не пугаемся, не разбегаемся – простейшие примеры с квадратными корнями, думаю, будут понятны широкому кругу студентов. Весь материал я постараюсь изложить максимально подробно и максимально просто.
На уроке мы разберем простейшие неопределенные интегралы от иррациональных функций, чуть более громоздкие (с разными корнями), и закончится повествование биномиальными интегралами, кои уже являются немного дебрями интегралов, где преподаватель-волк частенько кушает зайцев.
Итак, прошу любить и жаловать первый параграф
Интегралы от корней. Типовые методы и приемы решения
Вспоминаем счастливые школьные годы. Пыонеры на уроках математики, приступая к изучению корней, в первую очередь знакомятся с квадратным корнем. Мы пойдем тем же путем.
Пример 1
Найти
неопределенный интеграл
![]()
Анализируя подынтегральную функцию, приходишь к печальному выводу, что она совсем не напоминает табличные интегралы. Вот если бы всё это добро находилось в числителе – было бы просто. Или бы корня внизу не было. Или многочлена. Никакие методы интегрирования дробей тоже не помогают. Что делать?
Основной приём решения иррациональных интегралов – это замена переменной, которая избавит нас от ВСЕХ корней в подынтегральной функции.
Отмечу, что эта замена немного своеобразная, ее техническая реализация отличается от «классического» способа замены, который рассмотрен на уроке Метод замены в неопределенном интеграле.
В данном
примере нужно провести замену ![]() ,
то есть, вместо «икса» под корнем у нас
окажется
,
то есть, вместо «икса» под корнем у нас
окажется ![]() .
Почему замена именно такая? Потому-что
.
Почему замена именно такая? Потому-что ![]() ,
и в результате замены корень пропадёт.
,
и в результате замены корень пропадёт.
Если бы в
подынтегральной функции вместо
квадратного корня у нас находился ![]() ,
то мы бы провели замену
,
то мы бы провели замену ![]() .
Если бы там был
.
Если бы там был ![]() –
то
–
то ![]() и
так далее.
и
так далее.
Хорошо, ![]() у
нас превратится в
у
нас превратится в![]() .
Что произойдет с многочленом
.
Что произойдет с многочленом ![]() ?
Сложностей нет: если
?
Сложностей нет: если ![]() ,
то
,
то ![]() .
.
Осталось
выяснить, во что превратится дифференциал ![]() .
Делается это так:
.
Делается это так:
Берем нашу
замену ![]() и навешиваем
дифференциалы на обе части:
и навешиваем
дифференциалы на обе части:
![]() (я
распишу максимально подробно)
(я
распишу максимально подробно)
![]()
![]()
Оформление решения должно выглядеть примерно так:
![]()
Проведем
замену: ![]()
 (1)
Проводим подстановку после замены (как,
что и куда, уже рассмотрено).
(1)
Проводим подстановку после замены (как,
что и куда, уже рассмотрено).
(2) Выносим
константу за пределы интеграла. Числитель
и знаменатель сокращаем на ![]() .
.
(3) Получившийся интеграл является табличным, готовим его для интегрирования, выделяя квадрат
(4) Интегрируем
по таблице, используя формулу ![]() .
.
(5) Проводим
обратную замену. Как это делается?
Вспоминаем, от чего плясали: если ![]() ,
то
,
то ![]() .
.
Внимание! Для изучения дальнейших примеров необходимо хорошо проработать первый параграф урока Интегрирование некоторых дробей.
Пример 2
Найти
неопределенный интеграл
![]()
Это пример для самостоятельного решения. Полное решение и ответ в конце урока.
Как-то так
получилось, что в примерах 1, 2 «голый»
числитель с одиноким дифференциалом ![]() .
Что же. Исправим ситуацию.
.
Что же. Исправим ситуацию.
Пример 3
Найти
неопределенный интеграл
![]()
Предварительный анализ подынтегральной функции опять показывает, что лёгкого пути нет. А поэтому нужно избавляться от корня.
![]()
Проведем
замену: ![]() За
За ![]() обозначаем
ВСЁ выражение под корнем. Замена из
предыдущих примеров
обозначаем
ВСЁ выражение под корнем. Замена из
предыдущих примеров ![]() здесь
не годится (точнее, сделать-то её можно,
но это не избавит нас от корня).
Навешиваем
дифференциалы на обе части:
здесь
не годится (точнее, сделать-то её можно,
но это не избавит нас от корня).
Навешиваем
дифференциалы на обе части:
![]()
![]()
![]()
С числителем
разобрались. Что делать с ![]() в
знаменателе?
Берем нашу замену
в
знаменателе?
Берем нашу замену ![]() и
выражаем из неё:
и
выражаем из неё: ![]() Если
Если ![]() ,
то
,
то ![]()
 (1)
Проводим подстановку в соответствии с
выполненной заменой.
(2) Причесываем
числитель. Константу здесь я предпочел
не выносить за знак интеграла (можно
делать и так, ошибкой не будет)
(1)
Проводим подстановку в соответствии с
выполненной заменой.
(2) Причесываем
числитель. Константу здесь я предпочел
не выносить за знак интеграла (можно
делать и так, ошибкой не будет)
(3) Раскладываем числитель в сумму. Еще раз настоятельно рекомендую ознакомиться с первым параграфом урока Интегрирование некоторых дробей. Канители с разложением числителя в сумму в иррациональных интегралах будет предостаточно, очень важно отработать это прием.
(4) Почленно делим числитель на знаменатель.
(5) Используем
свойства линейности неопределенного
интеграла. Во втором интеграле выделяем
квадрат ![]() для
последующего интегрирования по таблице.
для
последующего интегрирования по таблице.
(6) Интегрируем
по таблице. Первый интеграл совсем
простой, во втором используем табличную
формулу высокого логарифма ![]() .
.
(7) Проводим
обратную замену. Если мы проводили
замену ![]() ,
то, обратно:
,
то, обратно: ![]()
Пример 4
Найти
неопределенный интеграл
![]()
Это пример для самостоятельного решения, если вы невнимательно проработали предыдущие примеры, то допустите ошибку! Полное решение и ответ в конце урока.
Принципиально
так же решаются интегралы с
несколькими одинаковыми корнями,
например ![]() ,
, ![]() и
т.д. А что делать, если в подынтегральной
функции корни разные?
и
т.д. А что делать, если в подынтегральной
функции корни разные?
Пример 5
Найти
неопределенный интеграл

Вот и пришла расплата за голые числители. Когда встречается такой интеграл, обычно становится страшно. Но страхи напрасны, после проведения подходящей замены подынтегральная функция упрощается. Задача состоит в следующем: провести удачную замену, чтобы сразу избавиться от ВСЕХ корней.
Когда даны
разные корни удобно придерживаться
следующей схемы решения. Сначала
выписываем на черновике подынтегральную
функцию, при этом все корни представляем
в виде ![]() :
:  .
Нас будут интересовать знаменатели степеней:
.
Нас будут интересовать знаменатели степеней:
 Записываем
эти знаменатели: 2, 3, 3.
Теперь нужно
найти наименьшее общее кратное чисел
2, 3, 3 – такое число, чтобы оно делилось
и на 2 и на 3 (в данном случае), кроме того,
это число должно быть как можно меньше.
Записываем
эти знаменатели: 2, 3, 3.
Теперь нужно
найти наименьшее общее кратное чисел
2, 3, 3 – такое число, чтобы оно делилось
и на 2 и на 3 (в данном случае), кроме того,
это число должно быть как можно меньше.
Очевидно, что наименьшим общим кратным является число 6. Оно делится и на 2 и на 3, кроме того, меньше шестерки ничего не придумать.
Как многие
уже догадались, замена в рассматриваемом
интеграле будет следующей: ![]()
Оформляем
решение:

Проведем
замену:![]()

(1) Производим подстановку.
(2) Избавляемся
от корней. Выносим константу за знак
интеграла. Сокращаем числитель и
знаменатель на ![]() .
.
(3) Сокращаем
числитель и знаменатель еще на ![]() .
.
(4) Раскладываем числитель в сумму (как это сделать, уже неоднократно упоминалось).
(5) Почленно делим числитель на знаменатель.
(6) Интегрируем по таблице. При этом константу я снова «прилепил» к каждому из трех слагаемых (можно этого и не делать, момент несущественный).
(7) Проводим
обратную замену. Если ![]() ,
то, обратно:
,
то, обратно: ![]() .
В ходе обратной замены некоторые корни
лучше сразу сократить (обычно это
делается устно). В рассмотренном примере
сокращение корней встретилось в первом
слагаемом:
.
В ходе обратной замены некоторые корни
лучше сразу сократить (обычно это
делается устно). В рассмотренном примере
сокращение корней встретилось в первом
слагаемом: ![]()
Как видите, особых сложностей нет, несмотря на то, что сначала интеграл показался трудным и страшным.
Пример 6
Найти
неопределенный интеграл
![]()
Это пример для самостоятельного решения.
Интегрирование биномиальных интегралов
Так называемый
биномиальный интеграл имеет следующий
вид: ![]() .
Такой интеграл берётся в трёх случаях.
.
Такой интеграл берётся в трёх случаях.
1) Случай
первый. Самый лёгкий.
Если степень ![]() –
целое число.
–
целое число.
Например: ![]()
Представим
интеграл в стандартном виде (это лучше
делать на черновике):
![]() Мы
видим, что степень
Мы
видим, что степень ![]() –
целая, а, значит, действительно имеет
место первый случай. На самом деле
биномиальный интеграл первого типа
решается практически так же, как интегралы
в примерах 5, 6, поэтому приводить почти
такие же решения особого смысла нет –
я просто покажу, какую замену здесь
нужно провести.
Смотрим на знаменатели
дробей:
–
целая, а, значит, действительно имеет
место первый случай. На самом деле
биномиальный интеграл первого типа
решается практически так же, как интегралы
в примерах 5, 6, поэтому приводить почти
такие же решения особого смысла нет –
я просто покажу, какую замену здесь
нужно провести.
Смотрим на знаменатели
дробей:
 Записываем
знаменатели: 2, 5. Находим наименьшее
общее кратное этих чисел. Очевидно, это
10: оно делится и на 2 и на 5, кроме того –
десятка самая маленькая в этом
смысле.
После замены
Записываем
знаменатели: 2, 5. Находим наименьшее
общее кратное этих чисел. Очевидно, это
10: оно делится и на 2 и на 5, кроме того –
десятка самая маленькая в этом
смысле.
После замены ![]() все
корни гарантировано пропадут. Повторюсь,
примеров для первого случая не будет,
так как они очень похожи на недавно
разобранные интегралы.
все
корни гарантировано пропадут. Повторюсь,
примеров для первого случая не будет,
так как они очень похожи на недавно
разобранные интегралы.
2) Случай второй
![]() Если
Если ![]() –
целое число, то необходимо провести
замену
–
целое число, то необходимо провести
замену ![]() ,
где
,
где ![]() –
знаменатель дроби
–
знаменатель дроби ![]() .
.
Спокойствие, только спокойствие, сейчас во всём разберемся.
Пример 7
Найти
неопределенный интеграл
![]()
Представим
интеграл в стандартном виде ![]() :
:
![]() .
Вообще говоря, формально правильнее
было записать
.
Вообще говоря, формально правильнее
было записать ![]() ,
но перестановка слагаемых в скобках не
играет никакой роли.
,
но перестановка слагаемых в скобках не
играет никакой роли.
Выписываем
степени:
![]() ,
, ![]() ,
, ![]() Сразу
проверяем, не относится ли наш интеграл
к первому случаю?
Сразу
проверяем, не относится ли наш интеграл
к первому случаю?
![]() –
целое? Нет.
Проверяем второй случай:
–
целое? Нет.
Проверяем второй случай:
![]() –
целое, значит у нас второй случай
Согласно
правилу для второго случая, необходимо
провести замену
–
целое, значит у нас второй случай
Согласно
правилу для второго случая, необходимо
провести замену ![]() ,
где
,
где ![]() –
знаменатель дроби
–
знаменатель дроби ![]() .
В рассматриваемом примере
.
В рассматриваемом примере ![]() ,
и знаменатель этой дроби равен «двойке».
Таким образом, чтобы гарантировано
избавиться от корня, нужно провести
замену
,
и знаменатель этой дроби равен «двойке».
Таким образом, чтобы гарантировано
избавиться от корня, нужно провести
замену ![]() .
.
Оформляем
решение:
![]()
Проведем
замену ![]() .
После
этой подстановки с корнем у нас будет
всё гуд:
.
После
этой подстановки с корнем у нас будет
всё гуд: ![]() Теперь
нужно выяснить, во что превратится оставшаяся
часть подынтегрального
выражения
Теперь
нужно выяснить, во что превратится оставшаяся
часть подынтегрального
выражения ![]() Берем
нашу замену
Берем
нашу замену ![]() и навешиваем дифференциалы
на обе части:
и навешиваем дифференциалы
на обе части:
 Но
вот, незадача, у нас
Но
вот, незадача, у нас ![]() ,
а нам нужно выразить
,
а нам нужно выразить ![]() .
Умножаем
обе части на
.
Умножаем
обе части на ![]() :
:
![]() Таким
образом:
Таким
образом: ![]() .
Уже лучше, но хотелось бы выразить
.
Уже лучше, но хотелось бы выразить ![]() только
через
только
через ![]() ,
а в правой части
,
а в правой части ![]() –
«икс» в квадрате внизу. Что делать?
Вспоминаем нашу замену
–
«икс» в квадрате внизу. Что делать?
Вспоминаем нашу замену ![]() и
выражаем из неё нужный нам
и
выражаем из неё нужный нам ![]() .
Окончательно:
.
Окончательно: ![]() .
Головоломно, но, увы, другие алгоритмы
еще запутаннее.
.
Головоломно, но, увы, другие алгоритмы
еще запутаннее.
Собственно, всё готово, продолжаем решение:

(1) Проводим подстановку согласно замене.
(2) Записываем компактно числитель.
(3) Раскладываем знаменатель в сумму.
(4) Почленно делим числитель на знаменатель.
(5) Интегрируем по таблице.
(6) Проводим
обратную замену: если ![]() ,
то
,
то ![]()
Пример 8
Найти
неопределенный интеграл
![]()
Это пример для самостоятельного решения. Полное решение и ответ в конце урока.
3) Случай третий. Самый сложный
![]() Если
Если ![]() –
целое число, то необходимо провести
замену
–
целое число, то необходимо провести
замену ![]() ,
где
,
где ![]() –
знаменатель дроби
–
знаменатель дроби ![]() .
.
Пример 9
Найти
неопределенный интеграл
![]()
Представим
интеграл в стандартном виде ![]() :
:
![]() .
.
Выписываем
степени и коэффициенты:
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]()
1) Не относится
ли наш интеграл к первому случаю?
![]() –
целое? Нет.
–
целое? Нет.
2) Проверяем
второй случай:
![]() –
целое? Нет.
–
целое? Нет.
3) ![]() –
целое! Значит, у нас третий случай.
–
целое! Значит, у нас третий случай.
Согласно
правилу для третьего случая, необходимо
провести замену ![]() ,
где
,
где ![]() –
знаменатель дроби
–
знаменатель дроби ![]() .
В рассматриваемом примере
.
В рассматриваемом примере ![]() ,
и знаменатель этой дроби равен опять
же «двойке». Коэффициенты (будьте
внимательны)
,
и знаменатель этой дроби равен опять
же «двойке». Коэффициенты (будьте
внимательны) ![]() ,
, ![]()
Таким
образом, чтобы гарантировано избавиться
от корня, нужно провести замену ![]() .
.
Оформляем решение:
![]()
Проведем
замену: ![]() .
.
Разбираемся
с корнем. Это труднее, чем в предыдущих
случаях.
Сначала из нашей замены ![]() нужно
выразить «икс квадрат»:
нужно
выразить «икс квадрат»:
![]() Теперь
подставляем
Теперь
подставляем ![]() под
корень:
под
корень:

На втором
этапе выясняем, во что превратится оставшаяся
часть подынтегрального выражения ![]() .
Берем нашу замену
.
Берем нашу замену ![]() и
навешиваем дифференциалы на обе части:
и
навешиваем дифференциалы на обе части:

Опять
проблема, в правой части у нас есть
«икс», а нам нужно всё выразить через
«тэ».
Берем ранее найденное выражение ![]() и
выражаем
и
выражаем ![]() Окончательно:
Окончательно:
![]()
В итоге мы
выразили через «тэ» и ![]() и
и ![]() ,
всё готово для продолжения решения:
,
всё готово для продолжения решения:

(1) Проводим подстановку согласно замене.
(2) Упрощаем выражение.
(3) Меняем знак в знаменателе и выносим минус за пределы интеграла (можно было не делать, но так удобнее).
(4) Проводим
обратную замену. В третьем случае
биномиального интеграла это тоже
труднее. Если изначальная замена ![]() ,
то
,
то ![]() .
.
(5) Избавляемся от четырехэтажности в логарифме.
3. Вычисление длины дуги плоской кривой
3.1 Если функция y = f(x) непрерывна вместе с её производной f'(x) на отрезке [a, b], то длина дуги AB, где A(a,f(a)), B(b, f(b)), выражается формулой
 . (28)
. (28)
3.2. Если
кривая задана параметрическими
уравнениями 
![]() ,
где x(t), y(t) - дифференцируемые
функции, то длина дуги
,
где x(t), y(t) - дифференцируемые
функции, то длина дуги
 . (29)
. (29)
3.3. Если
дуга задана в полярных координатах ![]() ,
, ![]() ,
то длина дуги
,
то длина дуги
 .
.
Определенный интеграл. Как вычислить площадь фигуры
Переходим к рассмотрению приложений интегрального исчисления. На этом уроке мы разберем типовую и наиболее распространенную задачу – как с помощью определенного интеграла вычислить площадь плоской фигуры. Наконец-то ищущие смысл в высшей математике – да найдут его. Мало ли. Придется вот в жизни приближать дачный участок элементарными функциями и находить его площадь с помощью определенного интеграла.
Для успешного освоения материала, необходимо:
1) Разбираться в неопределенном интеграле хотя бы на среднем уровне. Таким образом, чайникам для начала следует ознакомиться с уроком Неопределенный интеграл. Примеры решений.
2) Уметь применять формулу Ньютона-Лейбница и вычислять определенный интеграл. Наладить теплые дружеские отношения с определенными интегралами можно на страницеОпределенный интеграл. Примеры решений.
В действительности, для того чтобы находить площадь фигуры не надо так уж много знаний по неопределенному и определенному интегралу. Задание «вычислить площадь с помощью определенного интеграла» всегда предполагает построение чертежа, поэтому гораздо более актуальным вопросом будут ваши знания и навыки построения чертежей. В этой связи полезно освежить в памяти графики основных элементарных функций, а, как минимум, уметь строить прямую, параболу и гиперболу. Сделать это можно (многим – нужно) с помощью методического материала Графики и свойства элементарных функций и статьи огеометрических преобразованиях графиков.
Как обычно, весь материал изложен просто, подробно, с минимумом теории. Собственно, с задачей нахождения площади с помощью определенного интеграл все знакомы еще со школы, и мы мало уйдем вперед от школьной программы. Этой статьи вообще могло бы и не быть, но дело в том, что задача встречается в 99 случаев из 100, когда студент мучается от ненавистной вышки с увлечением осваивает курс высшей математики. . Начнем с криволинейной трапеции.
Криволинейной
трапецией называется плоская фигура,
ограниченная графиком некоторой
функции ![]() ,
осью
,
осью ![]() и
прямыми
и
прямыми ![]() ,
, ![]() :
:

Площадь
криволинейной трапеции численно равна
определенному интегралу  . У
любого определенного интеграла (который
существует) есть очень хороший
геометрический смысл. На уроке Определенный
интеграл. Примеры решений я
говорил, что определенный интеграл –
это число. А сейчас пришла пора
констатировать еще один полезный факт. С
точки зрения геометрии определенный
интеграл – это ПЛОЩАДЬ.
То
есть, определенному интегралу
(если он существует) геометрически
соответствует площадь некоторой фигуры.
Например, рассмотрим определенный
интеграл
. У
любого определенного интеграла (который
существует) есть очень хороший
геометрический смысл. На уроке Определенный
интеграл. Примеры решений я
говорил, что определенный интеграл –
это число. А сейчас пришла пора
констатировать еще один полезный факт. С
точки зрения геометрии определенный
интеграл – это ПЛОЩАДЬ.
То
есть, определенному интегралу
(если он существует) геометрически
соответствует площадь некоторой фигуры.
Например, рассмотрим определенный
интеграл ![]() .
Подынтегральная функция
.
Подынтегральная функция ![]() задает
на плоскости некоторую кривую (её можно
всегда при желании начертить), а сам
определенный интеграл
задает
на плоскости некоторую кривую (её можно
всегда при желании начертить), а сам
определенный интеграл ![]() численно
равен площади соответствующей
криволинейной трапеции.
численно
равен площади соответствующей
криволинейной трапеции.
Пример 1
Вычислить
площадь фигуры, ограниченной
линиями ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Это типовая формулировка задания. Первый и важнейший момент решения – построение чертежа. Причем, чертеж необходимо построить ПРАВИЛЬНО.
При построении чертежа я рекомендую следующий порядок: сначала лучше построить все прямые (если они есть) и только потом – параболы, гиперболы, графики других функций. Графики функций выгоднее строить поточечно, с техникой поточечного построения можно ознакомиться в справочном материале Графики и свойства элементарных функций. Там же можно найти очень полезный применительно к нашему уроку материал – как быстро построить параболу.
В данной
задаче решение может выглядеть
так.
Выполним чертеж (обратите внимание,
что уравнение ![]() задает
ось
задает
ось ![]() ):
):
 Штриховать
криволинейную трапецию я не буду, здесь
очевидно, о какой площади идет речь.
Решение продолжается так:
Штриховать
криволинейную трапецию я не буду, здесь
очевидно, о какой площади идет речь.
Решение продолжается так:
На
отрезке ![]() график
функции
график
функции ![]() расположен над
осью
расположен над
осью ![]() ,
поэтому:
,
поэтому:

Ответ: ![]()
У кого
возникли трудности с вычислением
определенного интеграла и применением
формулы Ньютона-Лейбница 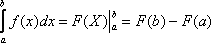 ,
обратитесь к лекции Определенный
интеграл. Примеры решений.
,
обратитесь к лекции Определенный
интеграл. Примеры решений.
После того, как задание выполнено, всегда полезно взглянуть на чертеж и прикинуть, реальный ли получился ответ. В данном случае «на глазок» подсчитываем количество клеточек в чертеже – ну, примерно 9 наберётся, похоже на правду. Совершенно понятно, что если бы у нас получился, скажем, ответ: 20 квадратных единиц, то, очевидно, что где-то допущена ошибка – в рассматриваемую фигуру 20 клеточек явно не вмещается, от силы десяток. Если ответ получился отрицательным, то задание тоже решено некорректно.
Пример 2
Вычислить
площадь фигуры, ограниченной
линиями ![]() ,
, ![]() ,
, ![]() и
осью
и
осью ![]()
Это пример для самостоятельного решения. Полное решение и ответ в конце урока.
Что делать,
если криволинейная трапеция расположена под
осью ![]() ?
?
Пример 3
Вычислить
площадь фигуры, ограниченной линиями ![]() ,
, ![]() и
координатными осями.
и
координатными осями.
Решение:
Выполним чертеж:
 Если
криволинейная трапеция полностью
расположена под осью
Если
криволинейная трапеция полностью
расположена под осью ![]() ,
то её площадь можно найти по формуле:
,
то её площадь можно найти по формуле:  В
данном случае:
В
данном случае:

Ответ: ![]()
Внимание! Не следует путать два типа задач:
1) Если Вам предложено решить просто определенный интеграл без всякого геометрического смысла, то он может быть отрицательным.
2) Если Вам предложено найти площадь фигуры с помощью определенного интеграла, то площадь всегда положительна! Именно поэтому в только что рассмотренной формуле фигурирует минус.
На практике чаще всего фигура расположена и в верхней и в нижней полуплоскости, а поэтому, от простейших школьных задачек переходим к более содержательным примерам.
Пример 4
Найти
площадь плоской фигуры, ограниченной
линиями ![]() ,
, ![]() .
.
Решение:
Сначала нужно выполнить чертеж. Вообще
говоря, при построении чертежа в задачах
на площадь нас больше всего интересуют
точки пересечения линий. Найдем точки
пересечения параболы ![]() и
прямой
и
прямой ![]() .
Это можно сделать двумя способами.
Первый способ – аналитический. Решаем
уравнение:
.
Это можно сделать двумя способами.
Первый способ – аналитический. Решаем
уравнение:

Значит,
нижний предел интегрирования ![]() ,
верхний предел интегрирования
,
верхний предел интегрирования ![]() .
Этим
способом лучше, по возможности, не
пользоваться.
.
Этим
способом лучше, по возможности, не
пользоваться.
Гораздо выгоднее и быстрее построить линии поточечно, при этом пределы интегрирования выясняются как бы «сами собой». Техника поточечного построения для различных графиков подробно рассмотрена в справке Графики и свойства элементарных функций. Тем не менее, аналитический способ нахождения пределов все-таки приходится иногда применять, если, например, график достаточно большой, или поточенное построение не выявило пределов интегрирования (они могут быть дробными или иррациональными). И такой пример, мы тоже рассмотрим.
Возвращаемся
к нашей задаче: рациональнее сначала
построить прямую и только потом параболу.
Выполним чертеж:
 Повторюсь,
что при поточечном построении пределы
интегрирования чаще всего выясняются
«автоматом».
Повторюсь,
что при поточечном построении пределы
интегрирования чаще всего выясняются
«автоматом».
А теперь
рабочая формула: Если на отрезке ![]() некоторая
непрерывная функция
некоторая
непрерывная функция ![]() больше
либо равна некоторой непрерывной
функции
больше
либо равна некоторой непрерывной
функции ![]() ,
то площадь соответствующей фигуры можно
найти по формуле:
,
то площадь соответствующей фигуры можно
найти по формуле: 
Здесь уже не надо думать, где расположена фигура – над осью или под осью, и, грубо говоря,важно, какой график ВЫШЕ (относительно другого графика), а какой – НИЖЕ.
В
рассматриваемом примере очевидно, что
на отрезке ![]() парабола
располагается выше прямой, а поэтому
из
парабола
располагается выше прямой, а поэтому
из ![]() необходимо
вычесть
необходимо
вычесть ![]()
Завершение решения может выглядеть так:
Искомая
фигура ограничена параболой ![]() сверху
и прямой
сверху
и прямой ![]() снизу.
На
отрезке
снизу.
На
отрезке ![]()
![]() ,
по соответствующей формуле:
,
по соответствующей формуле:

Ответ: ![]()
На самом
деле школьная формула для площади
криволинейной трапеции в нижней
полуплоскости (см. простенький пример
№3) – частный случай формулы  .
Поскольку ось
.
Поскольку ось ![]() задается
уравнением
задается
уравнением ![]() ,
а график функции
,
а график функции ![]() расположен
ниже оси
расположен
ниже оси ![]() ,
то
,
то 
А сейчас пара примеров для самостоятельного решения
Пример 5
Найти
площадь фигуры, ограниченной линиями ![]() ,
, ![]() .
.
Пример 6
Найти
площадь фигуры, ограниченной линиями ![]() ,
, ![]() .
.
В ходе решения задач на вычисление площади с помощью определенного интеграла иногда случается забавный казус. Чертеж выполнен правильно, расчеты – правильно, но по невнимательности… найдена площадь не той фигуры, именно так несколько раз лажался ваш покорный слуга. Вот реальный случай из жизни:
Пример 7
Вычислить
площадь фигуры, ограниченной
линиями ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Решение:
Сначала выполним чертеж:

…Эх, чертеж хреновенький вышел, но вроде всё разборчиво.
Фигура, площадь которой нам нужно найти, заштрихована синим цветом(внимательно смотрите на условие – чем ограничена фигура!). Но на практике по невнимательности нередко возникает «глюк», что нужно найти площадь фигуры, которая заштрихована зеленым цветом!
Этот пример еще и полезен тем, что в нём площадь фигуры считается с помощью двух определенных интегралов. Действительно:
1) На
отрезке ![]() над
осью
над
осью ![]() расположен
график прямой
расположен
график прямой ![]() ;
;
2) На
отрезке ![]() над
осью
над
осью ![]() расположен
график гиперболы
расположен
график гиперболы ![]() .
.
Совершенно очевидно, что площади можно (и нужно) приплюсовать, поэтому:

Ответ: ![]()
Переходим еще к одному содержательному заданию.
Пример 8
Вычислить
площадь фигуры, ограниченной
линиями ![]() ,
, ![]() Представим
уравнения в «школьном» виде
Представим
уравнения в «школьном» виде ![]() ,
, ![]() и
выполним поточечный чертеж:
и
выполним поточечный чертеж:
 Из
чертежа видно, что верхний предел у нас
«хороший»:
Из
чертежа видно, что верхний предел у нас
«хороший»: ![]() .
Но
чему равен нижний предел?! Понятно, что
это не целое число, но какое? Может
быть
.
Но
чему равен нижний предел?! Понятно, что
это не целое число, но какое? Может
быть ![]() ?
Но где гарантия, что чертеж выполнен с
идеальной точностью, вполне может
оказаться что
?
Но где гарантия, что чертеж выполнен с
идеальной точностью, вполне может
оказаться что ![]() .
Или корень. А если мы вообще неправильно
построили график?
.
Или корень. А если мы вообще неправильно
построили график?
В таких случаях приходиться тратить дополнительное время и уточнять пределы интегрирования аналитически.
Найдем
точки пересечения прямой ![]() и
параболы
и
параболы ![]() .
Для
этого решаем уравнение:
.
Для
этого решаем уравнение:


![]() ,
, ![]()
Действительно, ![]() .
.
Дальнейшее решение тривиально, главное, не запутаться в подстановках и знаках, вычисления здесь не самые простые.
На
отрезке ![]()
![]() ,
по соответствующей формуле:
,
по соответствующей формуле:

Ответ: ![]()
Ну, и в заключение урока, рассмотрим два задания сложнее.
Пример 9
Вычислить
площадь фигуры, ограниченной линиями ![]() ,
, ![]() ,
, ![]()
Решение:
Изобразим данную фигуру на чертеже.

Блин, забыл график подписать, а переделывать страницу, простите, не хотца.
Для поточечного построения чертежа необходимо знать внешний вид синусоиды (и вообще полезно знать графики всех элементарных функций), а также некоторые значения синуса, их можно найти в тригонометрической таблице. В ряде случаев (как в этом) допускается построение схематического чертежа, на котором принципиально правильно должны быть отображены графики и пределы интегрирования.
С пределами
интегрирования здесь проблем нет, они
следуют прямо из условия: ![]() –
«икс» изменяется от нуля до «пи».
Оформляем дальнейшее решение:
–
«икс» изменяется от нуля до «пи».
Оформляем дальнейшее решение:
На
отрезке ![]() график
функции
график
функции![]() расположен
над осью
расположен
над осью ![]() ,
поэтому:
,
поэтому:

(1) Как интегрируются синусы и косинусы в нечетных степенях можно посмотреть на урокеИнтегралы от тригонометрических функций. Это типовой прием, отщипываем один синус.
(2) Используем
основное тригонометрическое тождество
в виде ![]()
(3) Проведем
замену переменной ![]() ,
тогда:
,
тогда:
![]()
Новые
переделы интегрирования:
![]()
У кого совсем плохи дела с заменами, прошу пройти на урок Метод замены в неопределенном интеграле. Кому не очень понятен алгоритм замены в определенном интеграле, посетите страницу Определенный интеграл. Примеры решений.

(4) Здесь мы
использовали свойство определенного
интеграла 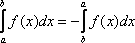 ,
расположив пределы интегрирования в
«привычном» порядке
,
расположив пределы интегрирования в
«привычном» порядке
Ответ: ![]() 1. Вычисление площади
плоской фигуры
1. Вычисление площади
плоской фигуры
1.1. Пусть
функция ![]() непрерывна
и неотрицательна на отрезке [a, b]. Тогда
площадь фигуры, ограниченной осью ОХ,
отрезками прямых x =a, x = b и
графиком функции
непрерывна
и неотрицательна на отрезке [a, b]. Тогда
площадь фигуры, ограниченной осью ОХ,
отрезками прямых x =a, x = b и
графиком функции ![]() ,
может быть вычислена по формуле
,
может быть вычислена по формуле  (см.
10.1 рис. 1).
(см.
10.1 рис. 1).
1.2. Если ![]() на
отрезке [a, b],
на
отрезке [a, b], ![]() - непрерывные
функции, то площадь фигуры, ограниченной
прямыми х = а, x = b,
графиками функций
- непрерывные
функции, то площадь фигуры, ограниченной
прямыми х = а, x = b,
графиками функций ![]() вычисляется
по формуле
вычисляется
по формуле  (рис.
10).
(рис.
10).
1.3. Если
функция ![]() на
отрезке [a, b]
принимает значения разных знаков,
то площадь фигуры, заключенная между
кривой
на
отрезке [a, b]
принимает значения разных знаков,
то площадь фигуры, заключенная между
кривой ![]() и
осью
и
осью ![]() , равна
, равна  (р
(р
2. Вычисление
площади криволинейного сектора. Пусть
кривая AB зада-на
в полярных координатах уравнением ![]() ,
, ![]() ,
причем
,
причем ![]() - непрерывная
и неотрицательная на отрезке
- непрерывная
и неотрицательная на отрезке ![]() функция.
Фигуру, ограниченную кривой AB и
двумя полярными радиусами, составляющими
с полярной осью углы
функция.
Фигуру, ограниченную кривой AB и
двумя полярными радиусами, составляющими
с полярной осью углы ![]() ,
будем называть криволинейным
сектором.
,
будем называть криволинейным
сектором.
Площадь криволинейного сектора может быть вычислена по формуле
 .
.
При вычислении
площади криволинейной трапеции, в случае
когда верхняя граница задана
параметрическими уравнениями  a £ t £ b в
формуле
a £ t £ b в
формуле  надо
сделать замену переменной, положив
надо
сделать замену переменной, положив ![]() ,
тогда получим
,
тогда получим  ,
где a и b -значения
параметра t,
соответствующие значениям x=a и x=b,
т. е.
,
где a и b -значения
параметра t,
соответствующие значениям x=a и x=b,
т. е. ![]() .
.
Основные свойства определённого интеграла.
Рассмотрим основные свойства определенного интеграла, считая подынтегральную функцию интегрируемой на отрезке [а; b]. При выводе свойств будем использовать определение интеграла и формулу Ньютона-Лейбница.
1.Если с — постоянное число и функция f(x) интегрируема на [а; b], то
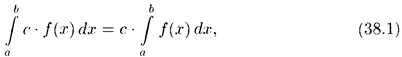 т.
е. постоянный множитель с можно выносить
за знак определенного интеграла.
Составим
интегральную сумму для функции с
• f(х). Имеем:
т.
е. постоянный множитель с можно выносить
за знак определенного интеграла.
Составим
интегральную сумму для функции с
• f(х). Имеем: Тогда
Тогда  .
Отсюда вытекает, что функция с •
f(x) интегрируема на [a; b] и
справедлива формула (38.1).
.
Отсюда вытекает, что функция с •
f(x) интегрируема на [a; b] и
справедлива формула (38.1).
2.Если
функции f1(x) и f2(x) интегрируемы на [а; b],
тогда интегрируема на [a; b] их сумма
и
 т.е.
интеграл от суммы равен сумме
интегралов.
т.е.
интеграл от суммы равен сумме
интегралов. Свойство
2 распространяется на сумму любого
конечного числа слагаемых.
Свойство
2 распространяется на сумму любого
конечного числа слагаемых. Это
свойство можно принять по определению.
Это свойство также подтверждается
формулой Ньютона -Лейбница.
Это
свойство можно принять по определению.
Это свойство также подтверждается
формулой Ньютона -Лейбница.
4.Если
функция f{x) интегрируема на[а; b] и a < с
< b, то т.е.
интеграл по всему отрезку равен сумме
интегралов по частям этого о гречка.
Это свойство называют аддитивностью определенного
интеграла (или свойством аддитивности).
При
разбиении отрезка [a; b] на части
включим точку с в число точек деления
(это можно сделать ввиду независимости
предела интегральной суммы от способа
разбиения отрезка [а; b] на части).
Если с = хm, то интегральную сумму
можно разбить на две суммы:
т.е.
интеграл по всему отрезку равен сумме
интегралов по частям этого о гречка.
Это свойство называют аддитивностью определенного
интеграла (или свойством аддитивности).
При
разбиении отрезка [a; b] на части
включим точку с в число точек деления
(это можно сделать ввиду независимости
предела интегральной суммы от способа
разбиения отрезка [а; b] на части).
Если с = хm, то интегральную сумму
можно разбить на две суммы: Каждая
из написанных сумм является интегральной
соответственно для отрезков [a; b],
[а; с] и [с; b]. Переходя к пределу
в последнем равенстве прип→∞ (λ→0),
получим равенство (38.3).
Свойство 4
справедливо при любом расположении
точек а, b, с (считаем. что
функция f(x) интегрируема на
большем из получающихся отрезков).
Так.
например, если а < b < с, то
Каждая
из написанных сумм является интегральной
соответственно для отрезков [a; b],
[а; с] и [с; b]. Переходя к пределу
в последнем равенстве прип→∞ (λ→0),
получим равенство (38.3).
Свойство 4
справедливо при любом расположении
точек а, b, с (считаем. что
функция f(x) интегрируема на
большем из получающихся отрезков).
Так.
например, если а < b < с, то От
сюда
От
сюда (использованы
свойства 4 и 3).
(использованы
свойства 4 и 3).
5.«Теорема
о среднем». Если функция f(x) непрерывна
на отрезке [a; b], то сyществует точка ![]() такая,
что
такая,
что По
формуле Ньютона-Лейбница имеем
По
формуле Ньютона-Лейбница имеем где F’(x)
= f(x). Применяя к разности F(b) —
F(a) теорему Лагранжа (теорему о
конечном приращении функции), получим
F(b)
— F(a) = F’(с) *(b-a) = f(c) *(b — a).
Свойство
5 («теорема о среднем») при f(x) ≥ 0
имеет простой геометрический смысл:
значение определенного интеграла равно,
при некотором
где F’(x)
= f(x). Применяя к разности F(b) —
F(a) теорему Лагранжа (теорему о
конечном приращении функции), получим
F(b)
— F(a) = F’(с) *(b-a) = f(c) *(b — a).
Свойство
5 («теорема о среднем») при f(x) ≥ 0
имеет простой геометрический смысл:
значение определенного интеграла равно,
при некотором ![]() ,
площади прямоугольника с высотой f(с)и
основанием b — а (см. рис. 170).
Число
,
площади прямоугольника с высотой f(с)и
основанием b — а (см. рис. 170).
Число называется
средним значением функции f(x) на
отрезке [a; b].
называется
средним значением функции f(x) на
отрезке [a; b].
6.Если
функция f(x) сохраняет знак на отрезке
[a; b], где а < b, то интеграл ![]() имеет
тот же знак, что и функция. Так.
если f(x) ≥ 0 на отрезке
[a; b], то
имеет
тот же знак, что и функция. Так.
если f(x) ≥ 0 на отрезке
[a; b], то  По
«теореме о среднем» (свойство 5)
По
«теореме о среднем» (свойство 5)

где ![]() .
А так как f(x) ≥ 0 для
всех
.
А так как f(x) ≥ 0 для
всех ![]() ,
то и
,
то и![]() Поэтому
Поэтому 
7.Неравенство
между непрерывными функциями на отрезке
[a; b], (а < b) можно интегрировать. Так,
если ![]()
 Так
как
Так
как ![]() ,
то при a < b, согласно свойству
6, имеем
,
то при a < b, согласно свойству
6, имеем

Или, согласно
свойству 2,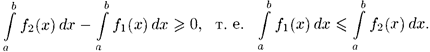 Отметим,
что дифференцировать неравенства
нельзя.
Отметим,
что дифференцировать неравенства
нельзя.
8. Оценка
интеграла. Если m и М — соответственно
наименьшее и наибольшее значения функции
у = f(x) на отрезке [а; b], (а < b), то Так
как для любого
Так
как для любого ![]() имеем m ≤ f(x) ≤ М,
то. согласно
свойству 7, имеем
имеем m ≤ f(x) ≤ М,
то. согласно
свойству 7, имеем Применяя
к крайним интегралам свойство 5,
получаем
Применяя
к крайним интегралам свойство 5,
получаем![]() Если f(x) ≥ 0,
то свойство 8 иллюстрируется геометрически:
площадь криволинейной трапеции заключена
между площадями прямоугольников,
основание которых есть [а; b], а высоты
равны mи М (см. рис.).
Если f(x) ≥ 0,
то свойство 8 иллюстрируется геометрически:
площадь криволинейной трапеции заключена
между площадями прямоугольников,
основание которых есть [а; b], а высоты
равны mи М (см. рис.).
9. Модуль
определенного интеграла не превосходит
интеграла от модуля подынтегральной
функции: Применяя
свойство 7 к очевидным неравенствам —
|f(x)| ≤ f(x) ≤ |f(x)|,
получаем
Применяя
свойство 7 к очевидным неравенствам —
|f(x)| ≤ f(x) ≤ |f(x)|,
получаем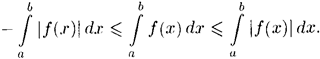 Отсюда
следует, что
Отсюда
следует, что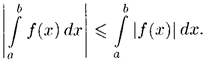 10. Производная
определенного интеграла по переменному
верхнему пределу равна подынтегральной
функции, в которой переменная
интегрирования, заменена этим пределом,
т.е.
10. Производная
определенного интеграла по переменному
верхнему пределу равна подынтегральной
функции, в которой переменная
интегрирования, заменена этим пределом,
т.е. По
формуле Ньютона-Лейбница
имеем:
По
формуле Ньютона-Лейбница
имеем: Следовательно,
Следовательно, Это
означает, что определенный интеграл
с переменным верхним пределом есть одна
аз первообразных подынтегральной
функции.
Это
означает, что определенный интеграл
с переменным верхним пределом есть одна
аз первообразных подынтегральной
функции.
Метод замены переменной в неопределенном интеграле. Примеры решений
На данном уроке мы познакомимся с одним из самых важных и наиболее распространенных приемов, который применяется в ходе решения неопределенных интегралов – методом замены переменной. Для успешного освоения материала требуются начальные знания и навыки интегрирования. Если есть ощущение пустого полного чайника в интегральном исчислении, то сначала следует ознакомиться с материалом Неопределенный интеграл. Примеры решений, где я объяснил в доступной форме, что такое интеграл и подробно разобрал базовые примеры для начинающих.
Технически метод замены переменной в неопределенном интеграле реализуется двумя способами:
– Подведение функции под знак дифференциала. – Собственно замена переменной.
По сути дела, это одно и то же, но оформление решения выглядит по-разному.
Начнем с более простого случая.
Подведение функции под знак дифференциала
На
уроке Неопределенный
интеграл. Примеры решений мы
научились раскрывать дифференциал,
напоминаю пример, который я приводил:
![]()
То есть, раскрыть дифференциал – это формально почти то же самое, что найти производную.
Пример 1
Найти
неопределенный интеграл. Выполнить
проверку.
![]()
Смотрим на
таблицу интегралов и находим похожую
формулу: ![]() .
Но проблема заключается в том, что у нас
под синусом не просто буковка «икс», а
сложное выражение. Что делать?
Подводим
функцию
.
Но проблема заключается в том, что у нас
под синусом не просто буковка «икс», а
сложное выражение. Что делать?
Подводим
функцию ![]() под
знак дифференциала:
под
знак дифференциала:
![]()
Раскрывая
дифференциал, легко проверить, что:

Фактически ![]() и
и ![]() –
это запись одного и того же.
–
это запись одного и того же.
Но, тем не
менее, остался вопрос, а как мы пришли
к мысли, что на первом шаге нужно записать
наш интеграл именно так: ![]() ?
Почему так, а не иначе?
?
Почему так, а не иначе?
Формула ![]() (и
все другие табличные формулы) справедливы
и применимы НЕ ТОЛЬКО для переменной
(и
все другие табличные формулы) справедливы
и применимы НЕ ТОЛЬКО для переменной ![]() ,
но и для любого сложного выражения ЛИШЬ
БЫ АРГУМЕНТ ФУНКЦИИ (
,
но и для любого сложного выражения ЛИШЬ
БЫ АРГУМЕНТ ФУНКЦИИ (![]() –
в нашем примере) И ВЫРАЖЕНИЕ ПОД
ЗНАКОМ ДИФФЕРЕНЦИАЛА БЫЛИ ОДИНАКОВЫМИ.
–
в нашем примере) И ВЫРАЖЕНИЕ ПОД
ЗНАКОМ ДИФФЕРЕНЦИАЛА БЫЛИ ОДИНАКОВЫМИ.
Поэтому
мысленное рассуждение при решении
должно складываться примерно так: «Мне
надо решить интеграл ![]() .
Я посмотрел в таблицу и нашел похожую
формулу
.
Я посмотрел в таблицу и нашел похожую
формулу ![]() .
Но у меня сложный аргумент
.
Но у меня сложный аргумент ![]() и
формулой я сразу воспользоваться не
могу. Однако если мне удастся получить
и
формулой я сразу воспользоваться не
могу. Однако если мне удастся получить ![]() и
под знаком дифференциала, то всё будет
нормально. Если я запишу
и
под знаком дифференциала, то всё будет
нормально. Если я запишу ![]() ,
тогда
,
тогда ![]() .
Но в исходном интеграле
.
Но в исходном интеграле ![]() множителя-тройки
нет, поэтому, чтобы подынтегральная
функция не изменилась, мне надо ее
домножить на
множителя-тройки
нет, поэтому, чтобы подынтегральная
функция не изменилась, мне надо ее
домножить на ![]() ».
В ходе примерно таких мысленных
рассуждений и рождается запись:
».
В ходе примерно таких мысленных
рассуждений и рождается запись:
![]() Теперь
можно пользоваться табличной формулой
Теперь
можно пользоваться табличной формулой ![]() :
:
 Готово
Готово
Единственное
отличие, у нас не буква «икс», а сложное
выражение ![]() .
.
Выполним
проверку. Открываем таблицу производных
и дифференцируем ответ:

Получена исходная подынтегральная функция, значит, интеграл найден правильно.
Обратите
внимание, что в ходе проверки мы
использовали правило дифференцирования
сложной функции ![]() . По
сути дела подведение функции под знак
дифференциала и
. По
сути дела подведение функции под знак
дифференциала и ![]() –
это два взаимно обратных правила.
–
это два взаимно обратных правила.
Пример 2
Найти
неопределенный интеграл. Выполнить
проверку.
![]()
Анализируем
подынтегральную функцию. Здесь у нас
дробь, причем в знаменателе линейная
функция (с «иксом» в первой степени).
Смотрим в таблицу интегралов и находим
наиболее похожую вещь: ![]() .
.
Подводим
функцию ![]() под
знак дифференциала:
под
знак дифференциала:
![]()
Те, кому
трудно сразу сообразить, на какую дробь
нужно домножать, могут быстренько на
черновике раскрыть дифференциал: ![]() .
Ага, получается
.
Ага, получается ![]() ,
значит, чтобы ничего не изменилось, мне
надо домножить интеграл на
,
значит, чтобы ничего не изменилось, мне
надо домножить интеграл на ![]() .
Далее
используем табличную формулу
.
Далее
используем табличную формулу ![]() :
:
![]()
Проверка:
 Получена
исходная подынтегральная функция,
значит, интеграл найден правильно.
Получена
исходная подынтегральная функция,
значит, интеграл найден правильно.
Пример 3
Найти
неопределенный интеграл. Выполнить
проверку.
![]()
Это пример для самостоятельного решения. Ответ в конце урока.
Пример 4
Найти
неопределенный интеграл. Выполнить
проверку.
![]()
Это пример для самостоятельного решения. Ответ в конце урока.
При определенном опыте решения интегралов, подобные примеры будут казаться лёгкими, и щелкаться как орехи:
![]()



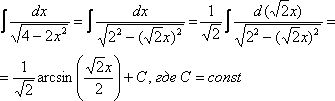
И так далее.
В конце
данного параграфа хотелось бы еще
остановиться на «халявном» случае,
когда в линейной функции переменная ![]() входит
с единичным коэффициентом, например:
входит
с единичным коэффициентом, например:
![]()
Строго
говоря, решение должно выглядеть так:
![]()
Как видите,
подведение функции ![]() под
знак дифференциала прошло «безболезненно»,
без всяких домножений. Поэтому на
практике таким длинным решением часто
пренебрегают и сразу записывают, что
под
знак дифференциала прошло «безболезненно»,
без всяких домножений. Поэтому на
практике таким длинным решением часто
пренебрегают и сразу записывают, что ![]() .
Но будьте готовы при необходимости
объяснить преподавателю, как Вы решали!
Поскольку интеграла
.
Но будьте готовы при необходимости
объяснить преподавателю, как Вы решали!
Поскольку интеграла ![]() в
таблице вообще-то нет.
в
таблице вообще-то нет.
Метод замены переменной в неопределенном интеграле
Переходим к рассмотрению общего случая – метода замены переменных в неопределенном интеграле.
Пример 5
Найти
неопределенный интеграл.
![]()
В качестве
примера я взял интеграл, который мы
рассматривали в самом начале урока. Как
мы уже говорили, для решения интеграла
нам приглянулась табличная формула ![]() ,
и всё дело хотелось бы свести к ней.
,
и всё дело хотелось бы свести к ней.
Идея метода
замены состоит в том, чтобы сложное
выражение (или некоторую функцию)
заменить одной буквой.
В данном
случае напрашивается: ![]() Вторая
по популярности буква для замены – это
буква
Вторая
по популярности буква для замены – это
буква ![]() .
В
принципе, можно использовать и другие
буквы, но мы всё-таки будем придерживаться
традиций.
.
В
принципе, можно использовать и другие
буквы, но мы всё-таки будем придерживаться
традиций.
Итак:  Но
при замене у нас остаётся
Но
при замене у нас остаётся ![]() !
Наверное, многие догадались, что если
осуществляется переход к новой
переменной
!
Наверное, многие догадались, что если
осуществляется переход к новой
переменной ![]() ,
то в новом интеграле всё должно быть
выражено через букву
,
то в новом интеграле всё должно быть
выражено через букву ![]() ,
и дифференциалу
,
и дифференциалу ![]() там
совсем не место.
Следует логичный
вывод, что
там
совсем не место.
Следует логичный
вывод, что ![]() нужно превратить
в некоторое выражение, которое зависит
только от
нужно превратить
в некоторое выражение, которое зависит
только от ![]() .
.
Действие
следующее. После того, как мы подобрали
замену, в данном примере, ![]() ,
нам нужно найти дифференциал
,
нам нужно найти дифференциал ![]() .
С дифференциалами, думаю, дружба уже у
всех налажена.
.
С дифференциалами, думаю, дружба уже у
всех налажена.
Так как ![]() ,
то
,
то
![]()
После
разборок с дифференциалом окончательный
результат рекомендую переписать
максимально коротко: ![]() Теперь
по правилам пропорции выражаем нужный
нам
Теперь
по правилам пропорции выражаем нужный
нам ![]() :
:
![]()
В
итоге:  Таким
образом:
Таким
образом:
![]() А
это уже самый что ни на есть табличный
интеграл
А
это уже самый что ни на есть табличный
интеграл ![]() (таблица,
интегралов, естественно, справедлива
и для переменной
(таблица,
интегралов, естественно, справедлива
и для переменной ![]() ).
).
![]() В
заключении осталось провести обратную
замену. Вспоминаем, что
В
заключении осталось провести обратную
замену. Вспоминаем, что ![]() .
.
 Готово.
Готово.
Чистовое оформление рассмотренного примера должно выглядеть примерно так:
“
![]()
Проведем
замену: ![]()
![]()
 “
“
Значок ![]() не
несет никакого математического смысла,
он обозначает, что мы прервали решение
для промежуточных объяснений.
не
несет никакого математического смысла,
он обозначает, что мы прервали решение
для промежуточных объяснений.
Также всем
рекомендую использовать математический
знак ![]() вместо
фразы «из этого следует это». И коротко,
и удобно.
вместо
фразы «из этого следует это». И коротко,
и удобно.
При оформлении
примера в тетради надстрочную
пометку ![]() обратной
замены лучше выполнять простым карандашом.
обратной
замены лучше выполнять простым карандашом.
Внимание! В
следующих примерах нахождение
дифференциала ![]() расписываться
подробно не будет.
расписываться
подробно не будет.
А теперь
самое время вспомнить первый способ
решения:

В чем разница? Принципиальной разницы нет. Это фактически одно и то же. Но с точки зрения оформления задания метод подведения функции под знак дифференциала – гораздо короче. Возникает вопрос. Если первый способ короче, то зачем тогда использовать метод замены? Дело в том, что для ряда интегралов не так-то просто «подогнать» функцию под знак дифференциала.
Пример 6
Найти
неопределенный интеграл.
![]()
Проведем
замену: ![]() (другую
замену здесь трудно придумать)
(другую
замену здесь трудно придумать)
![]()

Как видите, в результате замены исходный интеграл значительно упростился – свёлся к обычной степенной функции. Это и есть цель замены – упростить интеграл.
Ленивые продвинутые
люди запросто решат данный интеграл
методом подведения функции под знак
дифференциала:

Другое дело, что такое решение очевидно далеко не для всех студентов. Кроме того, уже в этом примере использование метода подведения функции под знак дифференциалазначительно повышает риск запутаться в решении.
Пример 7
Найти
неопределенный интеграл. Выполнить
проверку.
![]() Это
пример для самостоятельного решения.
Ответ в конце урока.
Это
пример для самостоятельного решения.
Ответ в конце урока.
Пример 8
Найти
неопределенный интеграл.
![]()
Замена: ![]() Осталось
выяснить, во что превратится
Осталось
выяснить, во что превратится ![]()
![]() Хорошо,
Хорошо, ![]() мы
выразили, но что делать с оставшимся в
числителе «иксом»?!
Время от времени
в ходе решения интегралов встречается
следующий трюк:
мы
выразили, но что делать с оставшимся в
числителе «иксом»?!
Время от времени
в ходе решения интегралов встречается
следующий трюк: ![]() мы
выразим из той же замены
мы
выразим из той же замены ![]() !
!
![]()

Готово.
Пример 9
Найти
неопределенный интеграл.
![]() Это
пример для самостоятельного решения.
Ответ в конце урока.
Это
пример для самостоятельного решения.
Ответ в конце урока.
Пример 10
Найти
неопределенный интеграл.
![]()
Наверняка некоторые обратили внимание, что в моей справочной таблице нет правила замены переменной. Сделано это сознательно. Правило внесло бы путаницу в объяснение и понимание, поскольку в вышерассмотренных примерах оно не фигурирует в явном виде.
Настало
время рассказать об основной предпосылке
использования метода замены переменной: в
подынтегральном выражении должна
находиться некоторая функция ![]() и
её производная
и
её производная ![]() :
: ![]() (функции
(функции ![]() ,
, ![]() могут
быть и не в произведении)
могут
быть и не в произведении)
В этой связи при нахождении интегралов довольно часто приходится заглядывать в таблицу производных.
В
рассматриваемом примере замечаем, что
степень числителя на единицу меньше
степени знаменателя. В таблице производных
находим формулу ![]() ,
которая как раз понижает степень на
единицу. А, значит, если обозначить
за
,
которая как раз понижает степень на
единицу. А, значит, если обозначить
за ![]() знаменатель,
то велики шансы, что числитель
знаменатель,
то велики шансы, что числитель ![]() превратится
во что-нибудь хорошее.
превратится
во что-нибудь хорошее.
![]()
Замена: ![]()
![]()
Кстати,
здесь не так сложно подвести функцию
под знак дифференциала:
![]()
Следует
отметить, что для дробей вроде![]() ,
, ![]() такой
фокус уже не пройдет (точнее говоря,
применить нужно будет не только прием
замены). Интегрировать некоторые дроби
можно научиться на уроке Интегрирование
некоторых дробей.
такой
фокус уже не пройдет (точнее говоря,
применить нужно будет не только прием
замены). Интегрировать некоторые дроби
можно научиться на уроке Интегрирование
некоторых дробей.
Вот еще пара типовых примеров для самостоятельного решения из той же оперы:
Пример 11
Найти
неопределенный интеграл.
![]()
Пример 12
Найти
неопределенный интеграл.
![]()
Решения в конце урока.
Пример 13
Найти
неопределенный интеграл.
![]()
Смотрим в
таблицу производных и находим наш
арккосинус: ![]() .
У нас в подынтегральном выражении
находится арккосинус и нечто похожее
на его производную.
.
У нас в подынтегральном выражении
находится арккосинус и нечто похожее
на его производную.
Общее
правило:
За ![]() обозначаем
саму функцию (а не её производную).
обозначаем
саму функцию (а не её производную).
В данном
случае: ![]() .
Осталось выяснить, во что превратится
оставшаяся часть подынтегрального
выражения
.
Осталось выяснить, во что превратится
оставшаяся часть подынтегрального
выражения ![]() .
.
В этом
примере нахождение ![]() я
распишу подробно поскольку
я
распишу подробно поскольку ![]() –
сложная функция.
–
сложная функция.
![]() Или
короче:
Или
короче: ![]() По
правилу пропорции выражаем нужный нам
остаток:
По
правилу пропорции выражаем нужный нам
остаток: ![]()
Таким
образом:
![]()
Вот здесь
подвести функцию под знак дифференциала
уже не так-то просто.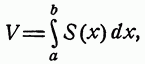
Как вычислить объем тела вращения с помощью определенного интеграла?
Помимо нахождения площади плоской фигуры с помощью определенного интегралаважнейшим приложением темы является вычисление объема тела вращения. Материал простой, но читатель должен быть подготовленным: необходимо уметь решатьнеопределенные интегралы средней сложности и применять формулу Ньютона-Лейбница в определенном интеграле. Как и для задачи нахождения площади, нужны уверенные навыки построения чертежей – это чуть ли не самое важное (поскольку интегралы сами по себе чаще будут лёгкими). Освоить грамотную и быструю технику построения графиков можно с помощью методических материалов Графики и свойства Элементарных функций иГеометрические преобразования графиков. Но, собственно, о важности чертежей я уже неоднократно говорил на уроке Определенный интеграл. Как вычислить площадь фигуры.
Вообще в интегральном исчислении очень много интересных приложений, с помощью определенного интеграла можно вычислить площадь фигуры, объем тела вращения, длину дуги, площадь поверхности тела и многое другое. Поэтому будет весело, пожалуйста, настройтесь на оптимистичный лад!
Представьте некоторую плоскую фигуру на координатной плоскости. Представили? ... Интересно, кто что представил… =))) Её площадь мы уже находили. Но, кроме того, данную фигуру можно ещё и вращать, причем вращать двумя способами:
– вокруг
оси абсцисс ![]() ;
–
вокруг оси ординат
;
–
вокруг оси ординат ![]() .
.
В данной
статье будут разобраны оба случая.
Особенно интересен второй способ
вращения, он вызывает наибольшие
затруднения, но на самом деле решение
практически такое же, как и в более
распространенном вращении вокруг оси
абсцисс. В качестве бонуса я вернусь
кзадаче
нахождения площади фигуры, и расскажу
вам, как находить площадь вторым способом
– по оси ![]() .
Даже не столько бонус, сколько материал
удачно вписывается в тему.
.
Даже не столько бонус, сколько материал
удачно вписывается в тему.
Начнем с наиболее популярной разновидности вращения.
Вычисление
объема тела, образованного вращением
плоской
фигуры вокруг оси ![]()
Пример 1
Вычислить
объем тела, полученного вращением
фигуры, ограниченной линиями ![]() ,
, ![]() вокруг
оси
вокруг
оси ![]() .
.
Решение: Как
и в задаче на нахождение площади, решение
начинается с чертежа плоской фигуры.
То есть, на плоскости ![]() необходимо
построить фигуру, ограниченную
линиями
необходимо
построить фигуру, ограниченную
линиями ![]() ,
, ![]() ,
при этом не забываем, что уравнение
,
при этом не забываем, что уравнение ![]() задаёт
ось
задаёт
ось ![]() .
Как рациональнее и быстрее выполнить
чертёж, можно узнать на страницах Графики
и свойства Элементарных функций и Определенный
интеграл. Как вычислить площадь фигуры.
Это китайское напоминание, и на данном
моменте я больше не останавливаюсь.
.
Как рациональнее и быстрее выполнить
чертёж, можно узнать на страницах Графики
и свойства Элементарных функций и Определенный
интеграл. Как вычислить площадь фигуры.
Это китайское напоминание, и на данном
моменте я больше не останавливаюсь.
Чертёж здесь довольно прост:

Искомая
плоская фигура заштрихована синим
цветом, именно она и вращается вокруг
оси ![]() .
В результате вращения получается такая
немного яйцевидная летающая тарелка,
которая симметрична относительно оси
.
В результате вращения получается такая
немного яйцевидная летающая тарелка,
которая симметрична относительно оси ![]() .
На самом деле у тела есть математическое
название, но в справочнике что-то лень
смотреть, поэтому едем дальше.
.
На самом деле у тела есть математическое
название, но в справочнике что-то лень
смотреть, поэтому едем дальше.
Как вычислить объем тела вращения?
Объем тела вращения можно вычислить по формуле:

В формуле
перед интегралом обязательно присутствует
число ![]() .
Так повелось – всё, что в жизни крутится,
связано с этой константой.
.
Так повелось – всё, что в жизни крутится,
связано с этой константой.
Как расставить пределы интегрирования «а» и «бэ», думаю, легко догадаться из выполненного чертежа.
Функция ![]() …
что это за функция? Давайте посмотрим
на чертеж. Плоская фигура ограничена
графиком параболы
…
что это за функция? Давайте посмотрим
на чертеж. Плоская фигура ограничена
графиком параболы ![]() сверху.
Это и есть та функция, которая
подразумевается в формуле.
сверху.
Это и есть та функция, которая
подразумевается в формуле.
В практических
заданиях плоская фигура иногда может
располагаться и ниже оси ![]() .
Это ничего не меняет – функция в формуле
возводится в квадрат:
.
Это ничего не меняет – функция в формуле
возводится в квадрат: ![]() ,
таким образом объем тела вращения
всегда неотрицателен, что весьма
логично.
,
таким образом объем тела вращения
всегда неотрицателен, что весьма
логично.
Вычислим
объем тела вращения, используя данную
формулу:

Как я уже отмечал, интеграл почти всегда получается простой, главное, быть внимательным.
Ответ: ![]()
Определение интеграла и его свойства
Определение. Пусть ![]() .
Пусть
.
Пусть ![]() ,
, ![]() аддитивна,
и ее плотность равна
аддитивна,
и ее плотность равна ![]() .
Тогда
.
Тогда ![]() называется
интегралом.
называется
интегралом.
Обозначение. Пусть ![]() .
Значение функции
.
Значение функции ![]() на
отрезке
на
отрезке ![]() :
:
![]()
Теорема
(Ньютон, Лейбниц). Пусть ![]() ,
, ![]() –
первообразная функции
–
первообразная функции ![]() .
Тогда
.
Тогда ![]()
![]()
Доказательство. По
теореме о плотности аддитивной функции
промежутка, ![]() и
равна плотности функции
и
равна плотности функции ![]() .
По определению тогда
.
По определению тогда ![]() –
интеграл функции
–
интеграл функции ![]() .
.
![]()
![]()
Свойства интеграла
1. ![]()
![]()
2. ![]() .
.
Доказательство. Пусть ![]() - первообразная
- первообразная ![]() ,
, ![]() –
первообразная
–
первообразная ![]() .
Тогда
.
Тогда ![]() –
первообразная
–
первообразная ![]() .
.

3. ![]() .
.
4. Пусть
функция ![]() ,
, ![]() дифференцируема.
Пусть функция
дифференцируема.
Пусть функция ![]() задана
на промежутке, содержащем множество
значений функции
задана
на промежутке, содержащем множество
значений функции ![]()
![]() ,
причем
,
причем ![]() .
Пусть у функции
.
Пусть у функции ![]() есть
первообразная. Тогда
есть
первообразная. Тогда
![]()
Доказательство. Пусть ![]() –
первообразная функции
–
первообразная функции ![]() .
Тогда
.
Тогда

Следствие. Пусть ![]() .
Тогда
.
Тогда
![]()
Доказательство. Положим ![]() ,
применим предыдущую теорему:
,
применим предыдущую теорему:
![]()
5. Пусть ![]() ,
функции
,
функции ![]() и
и ![]() дифференцируемы,
функция
дифференцируемы,
функция ![]() имеет
первообразную. Тогда
имеет
первообразную. Тогда
![]()
Доказательство.
![]()
Функции ![]() и
и ![]() имеют
первообразные, поэтому и функция
имеют
первообразные, поэтому и функция ![]() также
имеет первообразную, и можем записать
также
имеет первообразную, и можем записать

Определение. Пусть ![]() ,
, ![]() ,
, ![]() .
Тогда
.
Тогда
![]()
Задача
1. Пусть ![]() .
Докажите, что
.
Докажите, что
![]()
Выясните
при всех расположениях ![]() и
и ![]() с
помощью формулы Ньютона – Лейбница.
с
помощью формулы Ньютона – Лейбница.
6. Теорема об интеграле с переменным верхним пределом
Учитель Ньютона и его предшественник по кафедре в Кембриджском университете английский математик, философ и богослов Исаак Барроу (1630-1677) в детстве не проявлял интереса к учебе. В юношеские годы Исаак отличался веселым нравом и необыкновенным трудолюбием. Однажды на экзамене между капелланом и студентом Барроу произошел следующий диалог:
К а п е л л а н: Что такое вера?
Б а р р о у: То, чего не видишь.
К а п е л л а н: Что такое надежда?
Б а р р о у: Великое дело.
К а п е л л а н: Что такое любовь?
Б а р р о у: Большая редкость.
Дерзкие ответы Барроу возмутили капеллана, и он сообщил об этом епископу. Однако у епископа ответы Барроу вызвали лишь улыбку, и тем самым, инцидент был исчерпан.
Теорема
(Барроу). Пусть ![]() ,
функция
,
функция ![]() имеет
первообразную. Рассмотрим функцию
имеет
первообразную. Рассмотрим функцию ![]() ,
заданную на отрезке
,
заданную на отрезке ![]() по
правилу
по
правилу
![]()
Тогда ![]() .
.
Доказательство. Пусть ![]() –
одна из первообразных функции
–
одна из первообразных функции ![]() .
Тогда
.
Тогда
![]()
![]()
![]()
![]()
![]() -
первообразная
функции
-
первообразная
функции ![]() .
.
7. Пусть ![]() ,
функция
,
функция ![]() имеет
первообразную. Если
имеет
первообразную. Если ![]()
![]() ,
то
,
то ![]() .
.
Доказательство. Пусть ![]() .
.

Следовательно,
функция ![]() возрастает,
значит,
возрастает,
значит, ![]() .
.
8. Пусть ![]() ,
функции
,
функции ![]() и
и ![]() имеют
первообразные. Если
имеют
первообразные. Если ![]()
![]() ,
то
,
то
![]()
Доказательство.

9. Пусть ![]() ,
, ![]() имеют
первообразные,
имеют
первообразные, ![]() ,
, ![]() ,
, ![]()
![]() .
Тогда
.
Тогда ![]() .
.
Доказательство.

10. Пусть ![]() ,
функция
,
функция ![]() непрерывна.
Тогда
непрерывна.
Тогда
![]()
Доказательство.

Отсюда
![]()
Задача
2. Сформулируйте и докажите
утверждение для случая ![]() .
.
11. Теорема о среднем
Теорема. Пусть ![]() ,
функция
,
функция ![]() имеет
первообразную,
имеет
первообразную, ![]() и
и ![]() выполняется
неравенство
выполняется
неравенство
![]()
Тогда ![]() .
.
Доказательство. Проинтегрируем
неравенство и затем поделим получившееся
неравенство на ![]() .
.
Определение. Число ![]() называется
средним значением функции
называется
средним значением функции ![]() на
отрезке
на
отрезке ![]() .
.
|
Логарифмическое дифференцирование |
|
|
|
Логарифмическим дифференцированием называется метод дифференцирования функций, при котором сначала находится логарифм функции, а затем вычисляется производная от него. Такой прием позволяет эффективно вычислять производные степенных и рациональных функций. Рассмотрим этот подход более детально. Пусть дана функция y = f(x). Возьмем натуральные логарифмы от обеих частей:
Теперь продифференцируем это выражение как сложную функцию, имея ввиду, что y - это функция от x.
Отсюда видно, что искомая производная равна
|
|
Пример 1 |
|
|
|
Вычислить производную
функции Решение. Применяем логарифмическое дифференцирование: |
|
Пример 2 |
|
|
|
Найти производную
функции Решение. Прологарифмируем обе части и затем продифференцируем. |
|
Пример 3 |
|
|
|
Вычислить производную
функции Решение. Возьмем логарифм от обеих частей: Теперь продифференцируем левую и правую части: |
|
Пример 4 |
|
|
|
Продифференцировать Решение. Сначала возьмем логарифм от обеих частей: Дифференцируя левую и правую части соотношения, получаем Следовательно, производная равна |
Касательная к графику функции в точке. Уравнение касательной. Геометрический смысл производной.
Эту статью начнем с обзора необходимых определений и понятий.
Далее озвучим геометрический смысл производной, дадим пояснения и графическую иллюстрацию.
После этого перейдем к записи уравнения касательной прямой и приведем подробные решения самых характерных примеров и задач.
В заключении остановимся на нахождении уравнения касательной к кривым второго порядка, то есть, к окружности, эллипсу, гиперболе и параболе.
Навигация по странице.
-
Определения и понятия.
-
Геометрический смысл производной функции в точке.
-
Уравнение касательной прямой.
-
Касательная к окружности, эллипсу, гиперболе, параболе.
Определения и понятия.
Определение.
Углом
наклона прямой y=kx+b называют
угол ![]() ,
отсчитываемый от положительного
направления оси абсцисс до прямой y=kx+b в
положительном направлении (то есть,
против часовой стрелки).
,
отсчитываемый от положительного
направления оси абсцисс до прямой y=kx+b в
положительном направлении (то есть,
против часовой стрелки).

На рисунке положительное направление оси абсцисс показано горизонтальной зеленой стрелочкой, положительное направление отсчета угла изображено зеленой дугой, прямая показана синей линией, а угол наклона прямой - красной дугой.
Определение.
Угловым коэффициентом прямой y=kx+b называют числовой коэффициент k.
Угловой
коэффициент прямой равен тангенсу угла
наклона прямой, то есть, ![]() .
.
-
Угол наклона прямой равен нулю, когда прямая параллельна оси абсцисс. В этом случае нулю равен и угловой коэффициент, так как тангенс нуля есть ноль. Следовательно, уравнение прямой будет иметь вид y=b.
-
Когда угол наклона прямой y=kx+b является острым (
 или
или  ),
то угловой коэффициент k является
положительным числом (так как тангенс
острого угла
),
то угловой коэффициент k является
положительным числом (так как тангенс
острого угла  принимает
положительные значения
принимает
положительные значения  )
и указывает на возрастание графика
прямой.
)
и указывает на возрастание графика
прямой. -
В случае, когда
 прямая
располагается перпендикулярно оси
абсцисс (параллельно оси ординат) и
задается равенством x=c, где c -
некоторое действительное число.
прямая
располагается перпендикулярно оси
абсцисс (параллельно оси ординат) и
задается равенством x=c, где c -
некоторое действительное число. -
Когда угол наклона прямой y=kx+b является тупым (
 или
или  ),
то угловой коэффициент k является
отрицательным числом и указывает на
убывание графика прямой.
),
то угловой коэффициент k является
отрицательным числом и указывает на
убывание графика прямой.

Определение.
Прямую AB, проведенную через две точки графика функции y=f(x), называют секущей. Другими словами, секущая – это прямая, проходящая через две точки графика функции.

На рисунке
секущая прямая AB изображена
синей линией, график функции y=f(x) -
черной кривой, угол наклона секущей ![]() -
красной дугой.
-
красной дугой.
Если
принимать во внимание, что угловой
коэффициент прямой равен тангенсу угла
наклона (об этом говорили выше), и тангенс
угла в прямоугольном треугольнике ABC есть
отношение противолежащего катета к
прилежащему (это определение тангенса
угла), то для нашей секущей будет
справедлива серия равенств ![]() ,
где
,
где ![]() -
абсциссы точек А и В,
-
абсциссы точек А и В, ![]() -
соответствующие значения функции.
-
соответствующие значения функции.
То
есть, угловой коэффициент
секущей определяется равенством  или
или  ,
а уравнение секущей записывается
в виде
,
а уравнение секущей записывается
в виде  или
или  (при
необходимости обращайтесь к
разделу уравнение
прямой с угловым коэффициентом, проходящей
через заданную точку).
(при
необходимости обращайтесь к
разделу уравнение
прямой с угловым коэффициентом, проходящей
через заданную точку).
Секущая прямая разбивает график функции на три части: слева от точки А, от А до В и справа от точки В, хотя может иметь более чем две общих точки с графиком функции.
На рисунке ниже приведены три фактически разных секущих (точки А и В различны), но они совпадают и задаются одним уравнением.

Нам ни разу не встречались разговоры о секущей прямой для прямой. Но все же, если отталкиваться от определения, то прямая и ее секущая прямая совпадают.
В некоторых случаях секущая может иметь с графиком функции бесконечное число точек пересечения. Например, секущая, определяемая уравнением y=0, имеет бесконечное число общих точек с синусоидой.
Определение.
Касательной
к графику функции y=f(x) в
точке ![]() называют
прямую, проходящую через точку
называют
прямую, проходящую через точку ![]() ,
с отрезком которой практически сливается
график функции при значениях х сколь
угодно близких к
,
с отрезком которой практически сливается
график функции при значениях х сколь
угодно близких к ![]() .
.
Поясним
это определение на примере. Покажем,
что прямая y = x+1 является
касательной к графику функции ![]() в
точке (1; 2). Для этого покажем
графики этих функций при приближении
к точке касания (1; 2). Черным цветом
показан график функции
в
точке (1; 2). Для этого покажем
графики этих функций при приближении
к точке касания (1; 2). Черным цветом
показан график функции ![]() ,
касательная прямая показана синей
линией, точка касания изображена красной
точкой.
,
касательная прямая показана синей
линией, точка касания изображена красной
точкой.
Каждый последующий рисунок является увеличенной областью предыдущего (эти области выделены красными квадратами).

Хорошо
видно, что вблизи точки касания график
функции ![]() практически
сливается с касательной прямой y=x+1.
практически
сливается с касательной прямой y=x+1.
А сейчас перейдем к более значимому определению касательной.
Для этого покажем, что будет происходить с секущей АВ, если точку В бесконечно приближать к точке А.
Рисунок ниже иллюстрирует этот процесс.

Секущая АВ (показана
синей пунктирной прямой) будет стремиться
занять положение касательной прямой
(показана синей сплошной линией), угол
наклона секущей ![]() (показан
красной прерывистой дугой) будет
стремиться к углу наклона
касательной
(показан
красной прерывистой дугой) будет
стремиться к углу наклона
касательной ![]() (изображен
красной сплошной дугой).
(изображен
красной сплошной дугой).
Определение.
Таким
образом, касательная к графику
функции y=f(x) в точке А –
это предельное положение секущей AB при ![]() .
.
Вот теперь можно переходить к оописанию геометрического смысла производной функции в точке.
К началу страницы
Геометрический смысл производной функции в точке.
Рассмотрим
секущую АВ графика
функции y=f(x) такую, что
точки А и В имеют
соответственно координаты ![]() и
и ![]() ,
где
,
где ![]() -
приращение аргумента. Обозначим
через
-
приращение аргумента. Обозначим
через ![]() приращение
функции. Отметим все на чертеже:
приращение
функции. Отметим все на чертеже:

Из
прямоугольного треугольника АВС имеем ![]() .
Так как по определению касательная –
это предельное положение секущей, то
.
Так как по определению касательная –
это предельное положение секущей, то ![]() .
.
Вспомним определение
производной функции в точке: производной
функции y=f(x) в точке ![]() называется
предел отношения приращения функции к
приращению аргумента при
называется
предел отношения приращения функции к
приращению аргумента при ![]() ,
обозначается
,
обозначается ![]() .
.
Следовательно, ![]() ,
где
,
где ![]() -
угловой коэффициент касательной.
-
угловой коэффициент касательной.
Таким
образом, существование производной
функции y=f(x) в точке ![]() эквивалентно
существованию касательной к графику
функции y=f(x) в точке касания
эквивалентно
существованию касательной к графику
функции y=f(x) в точке касания ![]() ,
причемугловой коэффициент касательной
равен значению производной в точке
,
причемугловой коэффициент касательной
равен значению производной в точке ![]() ,
то есть
,
то есть ![]() .
.
Заключаем: геометрический смысл производной функции в точке состоит в существовании касательной к графику функции в этой точке.
К началу страницы
Уравнение касательной прямой.
Для записи
уравнения любой прямой на плоскости
достаточно знать ее угловой коэффициент
и точку, через которую она проходит.
Касательная прямая проходит через точку
касания и ее угловой коэффициент для
дифференцируемой функции равен значению
производной в точке ![]() .
То есть, из пункта геометрический
смысл производной функции в точке мы
можем взять все данные для записи
уравнения касательной прямой.
.
То есть, из пункта геометрический
смысл производной функции в точке мы
можем взять все данные для записи
уравнения касательной прямой.
Уравнение
касательной к графику функции y
= f(x) в точке ![]() имеет
вид
имеет
вид ![]() .
.
Мы
подразумеваем, что существует конечное
значение производной ![]() ,
в противном случае касательная прямая
либо вертикальна (если
,
в противном случае касательная прямая
либо вертикальна (если ![]() и
и ![]() ),
либо не существует (если
),
либо не существует (если ![]() ).
).
В зависимости
от углового коэффициента ![]() ,
касательная может быть параллельна оси
абсцисс (
,
касательная может быть параллельна оси
абсцисс (![]() ),
параллельна оси ординат (
),
параллельна оси ординат (![]() в
этом случае уравнение касательной будет
иметь вид
в
этом случае уравнение касательной будет
иметь вид ![]() ),
возрастать (
),
возрастать (![]() )
или убывать (
)
или убывать (![]() ).
).
Самое время привести несколько примеров для пояснения.
Пример.
Составить
уравнение касательной к графику
функции  в
точке (-1;-3) и определить угол
наклона.
в
точке (-1;-3) и определить угол
наклона.
Решение.
Функция
определена для всех действительных
чисел (при необходимости обращайтесь
к статье область
определения функции). Так как (-1;-3) –
точка касания, то ![]() .
.
Находим
производную (для этого может пригодиться
материал статьидифференцирование
функции, нахождение производной) и
вычисляем ее значение в точке ![]() :
:

Так как
значение производной в точке касания
есть угловой коэффициент касательной,
а он равен тангенсу угла наклона, то  .
.
Следовательно,
угол наклона касательной равен  ,
а уравнение касательной прямой имеет
вид
,
а уравнение касательной прямой имеет
вид

Графическая иллюстрация.
Черным цветом показан график исходной функции, касательная прямая изображена синей линией, точка касания - красной точкой. Рисунок справа представляет собой увеличенную область, обозначенную красным пунктирным квадратом на рисунке слева.

Пример.
Выяснить,
существует ли касательная к графику
функции ![]() в
точке (1; 1), если да, то составить
ее уравнение и определить угол ее
наклона.
в
точке (1; 1), если да, то составить
ее уравнение и определить угол ее
наклона.
Решение.
Областью определения функции является все множество действительных чисел.
Находим
производную:
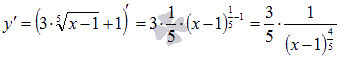
При ![]() производная
не определена, но
производная
не определена, но  и
и  ,
следовательно, в точке (1;1) существует
вертикальная касательная, ее уравнение
имеет вид x = 1, а угол наклона
равен
,
следовательно, в точке (1;1) существует
вертикальная касательная, ее уравнение
имеет вид x = 1, а угол наклона
равен ![]() .
.
Графическая иллюстрация.

Пример.
Найти все
точки графика функции ![]() ,
в которых:
a) касательная не
существует; b) касательная
параллельна оси абсцисс; c) касательная
параллельна прямой
,
в которых:
a) касательная не
существует; b) касательная
параллельна оси абсцисс; c) касательная
параллельна прямой  .
.
Решение.
Как всегда
начинаем с области определения функции.
В нашем примере функция определена на
всем множестве действительных чисел.
Раскроем знак модуля, для этого рассмотрим
два промежутка ![]() и
и ![]() :
:

Продифференцируем
функцию:
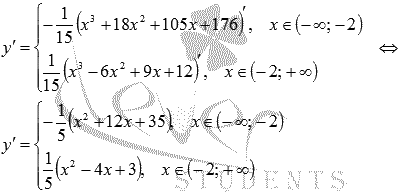
При x=-2 производная
не существует, так как односторонние
пределы в этой точке не равны:

Таким
образом, вычислив значение функции
при x=-2, мы можем дать ответ на
пункта): ![]() ,
касательная к графику функции не
существует в точке (-2;-2).
,
касательная к графику функции не
существует в точке (-2;-2).
b) Касательная
параллельна оси абсцисс, если ее угловой
коэффициент равен нулю (тангенс угла
наклона равен нулю). Так как ![]() ,
то нам нужно найти все значения х,
при которых производная функции
обращается в ноль. Эти значения и будут
абсциссами точек касания, в которых
касательная параллельна оси Ox.
,
то нам нужно найти все значения х,
при которых производная функции
обращается в ноль. Эти значения и будут
абсциссами точек касания, в которых
касательная параллельна оси Ox.
При ![]() решаем
уравнение
решаем
уравнение ![]() ,
а при
,
а при ![]() -
уравнение
-
уравнение ![]() :
:

Осталось
вычислить соответствующие значения
функции:

Поэтому,  -
искомые точки графика функции.
-
искомые точки графика функции.
Графическая иллюстрация.
График исходной функции изображен черной линией, красными точками отмечены найденные точки, в которых касательные параллельны оси абсцисс.

c) Если
две прямые на плоскости параллельны,
то их угловые коэффициенты равны (об
этом написано в статье параллельные
прямые, параллельность прямых). Исходя
из этого утверждения, нам нужно найти
все точки графика функции, в которых
угловой коэффициент касательной равен
восьми пятым. То есть, нам нужно решить
уравнение ![]() .
Таким образом, при
.
Таким образом, при ![]() решаем
уравнение
решаем
уравнение ![]() ,
а при
,
а при ![]() -
уравнение
-
уравнение ![]() .
.
Дискриминант
первого уравнения отрицателен,
следовательно, оно не имеет действительных
корней:

Второе
уравнение имеет два действительных
корня:

Находим
соответствующие значения функции:

В
точках  касательные
к графику функции параллельны прямой
касательные
к графику функции параллельны прямой  .
.
Графическая иллюстрация.
График
функции изображен черной линией, красной
линией показан график прямой  ,
синими линиями показаны касательные к
графику функции в точках
,
синими линиями показаны касательные к
графику функции в точках  .
.

Для тригонометрических функций в силу их периодичности, может существовать бесконечно много касательных прямых, имеющих один угол наклона (одинаковый угловой коэффициент).
Пример.
Написать
уравнения всех касательных к графику
функции  ,
которые перпендикулярны прямой
,
которые перпендикулярны прямой ![]() .
.
Решение.
Чтобы составить уравнение касательной к графику функции нам достаточно знать ее угловой коэффициент и координаты точки касания.
Угловой
коэффициент касательных ![]() найдем
из условия
перпендикулярности прямых: произведение
угловых коэффициентов перпендикулярных
прямых равно минус единице, то есть
найдем
из условия
перпендикулярности прямых: произведение
угловых коэффициентов перпендикулярных
прямых равно минус единице, то есть ![]() .
Так как по условию угловой коэффициент
перпендикулярной прямой равен
.
Так как по условию угловой коэффициент
перпендикулярной прямой равен ![]() ,
то
,
то ![]() .
.
Приступим к нахождению координат точек касания. Для начала найдем абсциссы, затем вычислим соответствующие значения функции – это будут ординаты точек касания.
При описании
геометрического смысла производной
функции в точке ![]() мы
отметили, что
мы
отметили, что ![]() .
Из этого равенства найдем абсциссы
точек касания.
.
Из этого равенства найдем абсциссы
точек касания.

Мы пришли
к тригонометрическому уравнению. Просим
обратить на него внимание, так как позже
мы его используем при вычислении ординат
точек касания. Решаем его (при затруднениях
обращайтесь к разделу решение
тригонометрических уравнений):

Абсциссы
точек касания найдены, вычислим
соответствующие ординаты (здесь
используем равенство, на которое мы
просили обратить внимание чуть выше):

Таким
образом,  -
все точки касания. Следовательно, искомые
уравнения касательных имеют вид:
-
все точки касания. Следовательно, искомые
уравнения касательных имеют вид:

Графическая иллюстрация.
На рисунке
черной кривой показан график исходной
функции на отрезке [-10;10], синими
линиями изображены касательные прямые.
Хорошо видно, что они перпендикулярны
красной прямой ![]() .
Точки касания отмечены красными точками.
.
Точки касания отмечены красными точками.

К началу страницы
Касательная к окружности, эллипсу, гиперболе, параболе.
До этого момента мы занимались нахождением уравнений касательных к графикам однозначных функций вида y = f(x) в различных точках. Канонические уравнения кривых второго порядка не являются однозначными функциями. Но окружность, эллипс, гиперболу и параболу мы можем представить комбинацией двух однозначных функций и уже после этого составлять уравнения касательных по известной схеме.
Касательная к окружности.
Окружность
с центром в точке ![]() и
радиусом R задается равенством
и
радиусом R задается равенством ![]() .
.
Запишем
это равенство в виде объединения двух
функций:

Здесь первая функция соответствует верхней полуокружности, вторая - нижней.

Таким
образом, чтобы составить уравнение
касательной к окружности в точке ![]() ,
принадлежащей верхней (или нижней)
полуокружности, мы находим уравнение
касательной к графику функции
,
принадлежащей верхней (или нижней)
полуокружности, мы находим уравнение
касательной к графику функции ![]() (или
(или ![]() )
в указанной точке.
)
в указанной точке.
Легко
показать, что в точках окружности с
координатами ![]() и
и ![]() касательные
параллельны оси абсцисс и задаются
уравнениями
касательные
параллельны оси абсцисс и задаются
уравнениями ![]() и
и ![]() соответственно
(на рисунке ниже они показаны синими
точками и синими прямыми), а в точках
соответственно
(на рисунке ниже они показаны синими
точками и синими прямыми), а в точках ![]() и
и ![]() -
параллельны оси ординат и имеют
уравнения
-
параллельны оси ординат и имеют
уравнения ![]() и
и ![]() соответственно
(на рисунке ниже они отмечены красными
точками и красными прямыми).
соответственно
(на рисунке ниже они отмечены красными
точками и красными прямыми).

К началу страницы
Касательная к эллипсу.
Эллипс с
центром в точке ![]() с
полуосями a и b задается
уравнением
с
полуосями a и b задается
уравнением  .
.
Эллипс
также как и окружность можно задать
объединением двух функций - верхнего и
нижнего полуэллипса:


Касательные в вершинах эллипса параллельны либо оси абсцисс (на рисунке ниже изображены синими прямыми), либо оси ординат (на рисунке ниже изображены красными прямыми).

Пример.
Написать
уравнения касательных к эллипсу ![]() в
точках с абсциссамиx=2.
в
точках с абсциссамиx=2.
Решение.
Найдем
сначала ординаты точек касания,
соответствующих абсциссам x=2.
Для этого подставим значение x=2 в
уравнение эллипса и решим полученное
уравнение относительно y:

Таким
образом, получаем две точки касания  и
и  ,
принадлежащие верхнему и нижнему
полуэллипсу соответственно.
,
принадлежащие верхнему и нижнему
полуэллипсу соответственно.
Найдем
уравнения полуэллипсов, для этого
разрешим уравнение эллипса относительноy:

То есть,
верхний полуэллипс задается функцией ![]() ,
а нижний -
,
а нижний - ![]() .
.
Теперь можем действовать по стандартному алгоритму для составления уравнения касательной к графику функции в точке.
Первая
касательная в точке  :
:
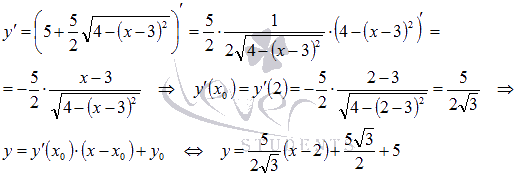
Вторая
касательная в точке  :
:

Графическая иллюстрация.

К началу страницы
Касательная к гиперболе.
Гипербола
с центром в точке ![]() и
вершинами
и
вершинами ![]() и
и ![]() задается
равенством
задается
равенством  (рисунок
ниже слева), а с вершинами
(рисунок
ниже слева), а с вершинами ![]() и
и ![]() -
равенством
-
равенством  (рисунок
ниже справа).
(рисунок
ниже справа).

В виде
объединения двух функций гипербола
представима как
 или
или  .
.

В вершинах гиперболы касательные параллельны оси Оу для первого случая и параллельны оси Ох для второго.
Таким образом, для нахождения уравнения касательной к гиперболе, выясняем какой функции принадлежит точка касания, и действуем обычным образом.
Возникает логичный вопрос, как определить какой из функций принадлежит точка. Для ответа на него подставляем координаты в каждое уравнение и смотрим, какое из равенств обращается в тождество. Рассмотрим это на примере.
Пример.
Составьте
уравнение касательной к гиперболе ![]() в
точке
в
точке ![]() .
.
Решение.
Запишем
гиперболу в виде двух функций:

Выясним к
какой функции принадлежит точка
касания ![]() .
.
Для первой
функции ![]() ,
следовательно, точка не принадлежит
графику этой функции.
,
следовательно, точка не принадлежит
графику этой функции.
Для второй
функции ![]() ,
следовательно, точка принадлежит графику
этой функции.
,
следовательно, точка принадлежит графику
этой функции.
Находим
угловой коэффициент касательной:

Таким
образом, уравнение касательной имеет
вид ![]() .
.
Графическая иллюстрация.

К началу страницы
Касательная к параболе.
Для
составления уравнения касательной к
параболе вида ![]() в
точке
в
точке ![]() пользуемся
стандартной схемой, и уравнение
касательной записываем как
пользуемся
стандартной схемой, и уравнение
касательной записываем как ![]() .
Касательная к графику такой параболы
в вершине параллельна осиОх.
.
Касательная к графику такой параболы
в вершине параллельна осиОх.
Параболу ![]() сначала
зададим объединением двух функций. Для
этого разрешим это уравнение
относительно y:
сначала
зададим объединением двух функций. Для
этого разрешим это уравнение
относительно y:


Теперь
выясняем к какой из функций принадлежит
точка касания ![]() и
действуем по стандартной схеме.
и
действуем по стандартной схеме.
Касательная к графику такой параболы в вершине параллельна оси Оу.
Пример.
Написать
уравнение касательной к графику
параболы ![]() ,
если угол наклона касательной равен
,
если угол наклона касательной равен ![]() .
.
Решение.
Представим
параболу через две функции:

Мы знаем,
что угловой коэффициент касательной
равен значению производной функции в
точке ![]() и
равен тангенсу угла наклона:
и
равен тангенсу угла наклона: ![]() .
Из этого равенства мы можем найти
абсциссу точки касания.
.
Из этого равенства мы можем найти
абсциссу точки касания.
Для первой
функции:

Полученное
уравнение действительных корней не
имеет, следовательно, к этой функции не
существует касательной с углом наклона ![]() .
.
Для второй
функции:

Получаем
точку касания  .
.
Таким
образом, уравнение искомой касательной
имеет вид  .
.
Графическая иллюстрация.

Непрерывность функции.
Пусть функция y = f(x) определена в точке x0 и в некоторой окрестности этой точки.
Функция y = f(x) называется непрерывной в точке x0, если существует предел функции в
этой точке и он равен значению функции в этой точке, т.е.
0
x x
lim f x f x
0
(1).
Равенство (1) означает выполнение трех условий:
1) функция f(x) определена в точке x0 и в ее окрестности;
2) функция f(x) имеет предел при x→x0;
3) предел функции в точке x0 равен значению функции в этой точке, то есть выпол-
няется равенство (1).
Это означает, что при нахождении предела непрерывной функции f(x) можно перей-
ти к пределу под знаком функции. То есть в функции f(x) вместо аргумента x подставить
его предельное значение x0.
Еще одно определение непрерывности функции можно дать, опираясь на понятия
приращения аргумента и функции.
Пусть функция y = f(x) определена в некотором интервале (a; b). Возьмем произволь-
ную точку x a; b 0 . Для любого x a; b разность x – x0 называется приращением ар-
гумента x в точке x0 и обозначается ∆x. ∆x = x – x0. x = ∆x + x0.
Разность соответствующих значений функций f(x) - f(x0) называется приращением
функции f(x) в точке x0 и обозначается ∆y (или ∆f, или ∆f (x0)): ∆y = f(x) - f (x0) или ∆y = f(x0
+ ∆x) - f (x0).
Очевидно, что приращения ∆x и ∆y могут быть как положительными, так и отрица-
тельными числами.
Перепишем равенство 0
x x
lim f x f x
0
используя обозначения приращений.
x→x0 можно переписать как x - x0→ 0, т.е. ∆x→ 0.
lim fx fx0
0
x x0
или lim y 0
x 0
(2).
То есть функция y = f(x) называется непрерывной в точке x0, если она определена в
точке x0 и ее окрестности и выполняется равенство (2), т.е. бесконечно малому прираще-
нию аргумента соответствует бесконечно малое приращение функции.
Функция y = f(x) называется непрерывной в интервале (a; b), если она непрерывна в
каждой точке этого интервала.
Функция y = f(x) называется непрерывной на отрезке [a; b], если она непрерывна в
интервале и в точке она непрерывна справа (т. е. lim fx fa
x a 0
), а в точке непрерывна
слева (т.е. lim fx fb
x b 0
).
Точки разрыва функции и их классификация.© Лекция подготовлена доц. Мусиной М.В.
Определение. Точки в которых нарушается непрерывность функции, называются
точками разрыва этой функции.
Если x = x0 – точка разрыва функции y = f(x), то в ней не выполняется по крайней ме-
ре одно из условий первого определения непрерывности функции, а именно.
1. Функция определена в окрестности точки x0, но не определена в самой точке x0.
2. Функция определена в точке x0 и ее окрестности, но не существует предела f(x)
при x→x0 .
3. Функции определена в точке x0 и ее окрестности, существует lim fx
0
xx
, но этот
предел не равен значению функции в точке x0: 0
x x
lim f x f x
0
.
Точки разрыва функции разделяются на точки разрыва первого и второго рода.
Точка x0 называется точкой разрыва первого рода функции y = f(x), если в этой точ-
ке существуют конечные пределы функции слева и справа (односторонние пределы), т.е.
1
x x 0
lim f x A
0
и 2
x x 0
lim f x A
0
.
При этом если А1 = А2, то точка x0 называется точкой устранимого разрыва, если А1
≠ А2 то точка x0 называется точкой конечного разрыва.
Точка разрыва называется точкой разрыва второго рода функции y = f(x), если по
крайней мере один из односторонних пределов (слева или справа) не существует или ра-
вен бесконечности.
Теоремы о непрерывных функциях.
Теорема 1. Сумма, произведение и частное двух непрерывных функций есть функ-
ция непрерывная (для частного за исключением тех значений аргумента, в которых дели-
тель равен нулю).
Теорема 2. Пусть функция u = φ(x) непрерывна в точке x0, а функция y = f(u) непре-
рывна в точке u0 = φ(x0). Тогда сложная функция f(φ(x)), состоящая из непрерывных функ-
ций, непрерывна в точке x0.
Теорема 3. Если функция y = f(x) непрерывна и строго монотонна на [a; b] оси Ох, то
обратная функция x = φ(y) также непрерывна и монотонна на соответствующем отрезке [c;
d] оси Оy.
Свойства функций, непрерывных на отрезке.
Теорема 1. (Вейерштрасса). Если функция непрерывна на отрезке, то она достигает
на этом отрезке своего наибольшего и наименьшего значений.
То есть существуют точки a, b и a, b, такие что f(α) ≤ f(x) ≤ f(β)
x a, b.
Следствие. Если функция непрерывна на отрезке, то она ограничена на нем.
То есть M 0 , такое, что fx M ,x a, b.
Теорема 2. (о промежуточном значении) (Больцано – Коши). Если функция y =
f(x) непрерывна на отрезке [a; b] и A fa, а B fb- значения функции на концах от-
резка, то C : A C B существует такое значение аргумента x
*
, что f(x
*
) = C.
Следствие. Если функция y = f(x) непрерывна на отрезке [a; b] и на его концах при-
нимает значения разных знаков, то внутри отрезка [a; b] найдется хотя бы одна точка с
такая, в ней функция f(x) обращается в ноль f(с) = 0.
Производная функции.© Лекция подготовлена доц. Мусиной М.В.
Понятие производной является одним из основных математических понятий. Произ-
водная широко используется при решении целого ряда задач математики, физики и других
наук, в особенности при изучении скорости разных процессов.
Задачи, приводящие к понятию производной.
Задача о касательной.
Возьмем точки М и М1, лежащие на непрерывной кривой L. Прямую, проходящую
через эти точки, называют секущей. Если точка М1будет двигаться по кривой по направ-
лению к М, то секущая, поворачиваясь около точки М, стремится к некоторому предель-
ному положению МТ.
Определение. Касательной к данной кривой в данной точке М называется пре-
дельное положение МТ секущей ММ1, проходящей через точку М, когда вторая точка пе-
ресечения М1 неограниченно приближается по кривой к точке М.
Задача. Зная уравнение непрерывной линии y = f(x) найти уравнение касательной в
данной ее точке.
Рассмотрим график непрерывной кривой y = f(x), имеющей в точке М (x, y) неверти-
кальную касательную. Найдем ее угловой коэффициент k = tg α, где α – угол касательной с
осью Ох.
Для этого возьмем на кривой точку М1 с абсциссой x+∆x и проведем секущую ММ1. φ
– угол наклона секущей. Очевидно, что угловой коэффициент секущей
x
f x x f x
x
y
kсек tg
Устремим точку М1 к точке М. То есть ∆x→0. В силу непрерывности функции f(x)
∆y→0 и точка М1 неограниченно приближается по кривой к точке М, а секущая стремится
к своему предельному положению касательной МТ. При этом φ→α, и если касательная не
перпендикулярна оси Ох, то в силу непрерывности tgx tg φ → tg α. Таким образом полу-
чим угловой коэффициент касательной
x
f x x f x
lim
x
y
k tg lim tg lim
x 0 x 0 x 0
.
Предел, стоящий в правой части равенства называют производной функции f(x) и
обозначают одним из символов y, f x,
dx
dy
, f x x
, x
y .
x
f x x f x
lim
x
y
y lim
x 0 x 0
.
Таким образом, мы получили, что угловой коэффициент касательной равен значению
ее производной в точке касания.
k tg y
Определение. Производной функции y = f(x) в точке x0 называется предел отношения
приращения функции к приращению аргумента, когда приращение аргумента стремится к
нулю.© Лекция подготовлена доц. Мусиной М.В.
x
f x x f x
y lim 0 0
x 0
Функция y = f(x), имеющая производную в каждой точке интервала (a; b) называет-
ся дифференцируемой в этом интервале, а операция нахождения производной функции
называется дифференцированием.
Задача о скорости движения материальной точки.
Пусть материальная точка М движется неравномерно по некоторой прямой по закону
S = S(t), где t - время, S - координата точки (расстояние до начала координат т.О). Это
уравнение – уравнение движения, оно выражает закон движения точки.
Задача. Зная закон движения точки, найти скорость движущейся точки в любой мо-
мент времени.
Пусть в некоторый момент времени времени t, точка занимает положение М: OM = x
= S(t), через время ∆t, т.е. в момент t + ∆t, точка окажется в M1, где ОM1 = S + ∆S = S(t +
∆t). За время ∆t, точка проходит путь ∆S = S(t + ∆t) – S(t).
Отношение
t
S
- средняя скоростью точки за время ∆t. Чем меньше ∆t, тем точнее
она выражает скорость движения точки в данный момент времени t. Предел средней ско-
рости движении при ∆t →0 называется скоростью движения точки в данный момент
времени (или мгновенной скоростью).
t
S t t S t
lim
t
S t
V lim
t 0 t 0
.
По аналогии с задачей о касательной можно сказать, что полученное выражение
представляет собой производную функции S по переменной t, т.е.
V St
Таким образом, скорость прямолинейного движения равна производной от пути по
времени. В этом заключается механический смысл производной.
Физический и геометрический смысл производной. Уравнение касательной и
нормали к кривой.
Обобщая, можно сказать, что если функция y = f(x) описывает какой-либо физиче-
ский процесс, то производная y' есть скорость протекания этого процесса. В этом со-
стоит физический смысл производной.
Вернемся к задаче о касательной. Мы нашли, что угловой коэффициент равен
k tg y, то есть f x tg k , то есть производная f '(x) в точке х равна угловому
коэффициенту касательной к графику функции y = f(x) в точке абсцисса которой равна х.
В этом заключается геометрический смысл производной.© Лекция подготовлена доц. Мусиной М.В.
Пусть точка касания М имеет координаты (x0, y0), тогда ее угловой коэффициент
k = f '(x0). Так как касательная пройдет через точку касания М, используем уравнение (из
аналитической геометрии) 0 0
y y k x x и перепишем его в виде
y y f x (x x ) 0 0 0
Это уравнение касательной.
Прямая, перпендикулярная касательной в точке касания, называется нормалью к
кривой.
Так как нормаль перпендикулярна касательной используем условие перпендикуляр-
ности для нахождения ее углового коэффициента.
кас 0
норм f x
1
k
1
k
.
Поэтому уравнение нормали:
(x x )
f x
1
y y 0
0
0
, f x0
0 .
Связь между непрерывностью и дифференцируемостью функции.
Теорема. Если функция дифференцируема в некоторой точке, то она непрерывна в
ней.
Доказательство.
Пусть функция y = f(x) дифференцируема в точке х, т.е.
y
x
y
lim
x 0
Запишем тождество x
x
y
y
. Отсюда
x y lim x y 0 0
x
y
lim y lim
x 0 x 0 x 0
Следовательно, функция y = f(x) непрерывна в точке х.
Обратная теорема неверна: непрерывная функция может не иметь производной.
Следствие. Если функция разрывна в некоторой точке, то она не имеет производной
в этой точке.
Основные правила дифференцирования функций.
Пусть функции u = u(x) и v = v(x) – две дифференцируемые в некотором интервале
(a; b) функции.
1. Производная суммы (разности) двух функций равна сумме (разности) производ-
ных этих функций.
(u v ) u v
2. Производная произведения двух функций равна произведению первого сомножи-
теля на второй плюс произведение первого сомножителя на производную второго:
(u v ) uv vu .© Лекция подготовлена доц. Мусиной М.В.
Доказательство:
y u v
y (u u )(v v ) uv y uv vu uv uv uv
x
u v
lim
x
v
lim u
x
u
lim v
x
y
lim
x 0 x 0 x 0 x 0
(uv ) vu uv
Следствие: Постоянный множитель можно выносить за знак производной.
y C u C u
3. Производная частного двух функций
vx
u x
, если v '(x) ≠ 0 равна дроби, числитель
которой есть разность произведений знаменателя дроби на производную числителя и чис-
лителя дроби на производную знаменателя, а знаменатель есть квадрат прежнего знамена-
теля: 2
v
u v v u
v
u
, v '(x) ≠ 0.
Производная сложной и обратной функций.
Пусть y = f(u) и u = φ(x), тогда y = f(φ(x)) – сложная функция с промежуточным аргу-
ментом u и независимой переменной x.
Теорема. Если функция u = φ(x) имеет производную ux' в точке х, а функция y = f(u)
имеет производную yu' в соответствующей точке u = φ(x), то сложная функция y = f(φ(x))
имеет производную yx' в точке х, которая находится по формуле x u ux
y y .
То есть для нахождения производной сложной функции надо производную данной
функции по промежуточному аргументу умножить на производную промежуточного
аргумента по независимой переменной.
Это остается в силе, если промежуточных аргументов несколько.
Правило. Если подлежащая дифференцированию функция является результатом це-
лого ряда действий над переменной х, то за промежуточный аргумент следует принять ре-
зультат всех этих действий кроме последнего.
Теорема. Если функция y = f(x) строго монотонна на интервале (a; b) и имеет не-
равную нулю производную f '(x) в произвольной точке этого интервала, то обратная ей
функция x = φ(y) также имеет производную φ '(y) в соответствующей точке, определяе-
мую равенством
f x
1
y
или
x
y
y
1
x
.
Таким образом, производная обратной функции равна обратной величине произ-
водной данной функции
Основные неопределенности пределов и их раскрытие.
С непосредственным вычислением пределов основных элементарных функций разобрались.
При переходе к функциям более сложного вида мы обязательно столкнемся с появлением выражений, значение которых не определено. Такие выражения называютнеопределенностями.
Перечислим
все основные виды неопределенностей:
ноль делить на ноль ![]() (0
на 0), бесконечность делить на
бесконечность
(0
на 0), бесконечность делить на
бесконечность ![]() ,
ноль умножить на бесконечность
,
ноль умножить на бесконечность ![]() ,
бесконечность минус бесконечность
,
бесконечность минус бесконечность ![]() ,
единица в степени бесконечность
,
единица в степени бесконечность ![]() ,
ноль в степени ноль
,
ноль в степени ноль ![]() ,
бесконечность в степени ноль
,
бесконечность в степени ноль ![]() .
.
ВСЕ ДРУГИЕ ВЫРАЖЕНИЯ НЕОПРЕДЕЛЕННОСТЯМИ НЕ ЯВЛЯЮТСЯ И ПРИНИМАЮТ ВПОЛНЕ КОНКРЕТНОЕ КОНЕЧНОЕ ИЛИ БЕСКОНЕЧНОЕ ЗНАЧЕНИЕ.
Раскрывать неопределенности позволяет:
-
упрощение вида функции (преобразование выражения с использованием формул сокращенного умножения, тригонометрических формул, домножением на сопряженные выражения с последующим сокращением и т.п.);
-
использование замечательных пределов;
-
применение правила Лопиталя;
-
использование замены бесконечно малого выражения ему эквивалентным(использование таблицы эквивалентных бесконечно малых).
Сгруппируем неопределенности в таблицу неопределенностей. Каждому виду неопределенности поставим в соответствие метод ее раскрытия (метод нахождения предела).
Эта таблица вместе с таблицей пределов основных элементарных функций будут Вашими главными инструментами при нахождении любых пределов.

Приведем парочку примеров, когда все сразу получается после подстановки значения и неопределенности не возникают.
Пример.
Вычислить
предел 
Решение.
Подставляем
значение:

И сразу получили ответ.
Ответ:

Пример.
Вычислить
предел ![]()
Решение.
Подставляем
значение х=0 в основание нашей
показательно степенной функции:
![]()
То есть,
предел можно переписать в виде
![]()
Теперь
займемся показателем. Это есть степенная
функция ![]() .
Обратимся ктаблице
пределов для степенных функций с
отрицательным показателем. Оттуда
имеем
.
Обратимся ктаблице
пределов для степенных функций с
отрицательным показателем. Оттуда
имеем![]() и
и ![]() ,
следовательно, можно записать
,
следовательно, можно записать ![]() .
.
Исходя из
этого, наш предел запишется в виде:
![]()
Вновь
обращаемся к таблице пределов, но уже
для показательных функций с основанием
большим единицы, откуда имеем:
![]()
Ответ:
![]()
Разберем на примерах с подробными решениями раскрытие неопределенностей преобразованием выражений.
Очень часто выражение под знаком предела нужно немного преобразовать, чтобы избавиться от неопределенностей.
Пример.
Вычислить
предел 
Решение.
Подставляем
значение:

Пришли к
неопределенности. Смотрим в таблицу
неопределенностей для выбора метода
решения. Пробуем упростить выражение.

После преобразования неопределенность раскрылась.
Ответ:
![]()
Пример.
Вычислить
предел ![]()
Решение.
Подставляем
значение:

Пришли к неопределенности (0 на 0). Смотрим в таблицу неопределенностей для выбора метода решения и пробуем упростить выражение. Домножим и числитель и знаменатель на выражение, сопряженное знаменателю.
Для
знаменателя сопряженным выражением
будет ![]()

Знаменатель
мы домножали для того, чтобы можно было
применить формулу сокращенного умножения
– разность квадратов и затем сократить
полученное выражение.

После ряда преобразований неопределенность исчезла.
Ответ:
![]()
ЗАМЕЧАНИЕ: для пределов подобного вида способ домножения на сопряженные выражения является типичным, так что смело пользуйтесь.
Пример.
Вычислить
предел 
Решение.
Подставляем
значение:

Пришли к неопределенности. Смотрим в таблицу неопределенностей для выбора метода решения и пробуем упростить выражение. Так как и числитель и знаменатель обращаются в ноль при х=1, то если разложить на множители эти выражения, можно будет сократить (х-1) и неопределенность исчезнет.
Разложим
числитель на множители:

Разложим
знаменатель на множители:

Наш предел
примет вид:

После преобразования неопределенность раскрылась.
Ответ:
![]()
Рассмотрим пределы на бесконечности от степенных выражений. Если показатели степенного выражения положительны, то предел на бесконечности бесконечен. Причем основное значение имеет наибольшая степень, остальные можно отбрасывать.
Пример.
![]()
Пример.
![]()
Если
выражение под знаком предела представляет
собой дробь, причем и числитель и
знаменатель есть степенные выражения
(m – степень числителя, а n –
степень знаменателя), то при ![]() возникает
неопределенность вида бесконечность
на бесконечность
возникает
неопределенность вида бесконечность
на бесконечность ![]() ,
в этом случае неопределенность
раскрывается делением и числитель
и знаменатель на
,
в этом случае неопределенность
раскрывается делением и числитель
и знаменатель на ![]()
Пример.
Вычислить
предел 
Решение.
 Степень
числителя равна семи, то есть m=7.
Степень знаменателя также равна семиn=7.
Разделим и числитель и знаменатель
на
Степень
числителя равна семи, то есть m=7.
Степень знаменателя также равна семиn=7.
Разделим и числитель и знаменатель
на ![]() .
.

Ответ:
![]()
Пример.
Вычислить
предел 
Решение.
 Степень
числителя 8/3, степень знаменателя 2.
Разделим и числитель и знаменатель
на
Степень
числителя 8/3, степень знаменателя 2.
Разделим и числитель и знаменатель
на ![]() .
.

Ответ:

Пример.
Вычислить
предел 
Решение.
 Степень
числителя 3, степень знаменателя 10/3.
Разделим и числитель и знаменатель
на
Степень
числителя 3, степень знаменателя 10/3.
Разделим и числитель и знаменатель
на![]() .
.

Ответ:

ВЫВОД.
Таким образом, возможны три варианта для предела отношения степенных выражений:
-
Если m равно n, то предел равен отношению коэффициентов при старших степенях;
-
Если m больше n, то предел равен бесконечности;
-
Если m меньше n, то предел равен 0.
Несобственный интеграл
Материал из Википедии — свободной энциклопедии
Определённый интеграл называется несобственным, если выполняется, по крайней мере, одно из следующих условий:
-
Предел a или b (или оба предела) являются бесконечными;
-
Функция f(x) имеет одну или несколько точек разрыва внутри отрезка [a, b].
Содержание
-
1 Несобственные интегралы I рода
-
1.1 Геометрический смысл несобственного интеграла I рода
-
1.2 Примеры
-
-
2 Несобственные интегралы II рода
-
2.1 Геометрический смысл несобственных интегралов II рода
-
2.2 Пример
-
-
3 Отдельный случай
-
4 Критерий Коши
-
5 Абсолютная сходимость
-
6 Условная сходимость
-
7 См. также
-
8 Список используемой литературы
Несобственные
интегралы I родаПусть ![]() определена
и непрерывна на множестве от
определена
и непрерывна на множестве от ![]() и
и  .
Тогда:
.
Тогда:
-
Если
 ,
то используется обозначение
,
то используется обозначение  и
интеграл называется несобственным
интегралом Римана первого рода. В
этом случае
и
интеграл называется несобственным
интегралом Римана первого рода. В
этом случае  называется
сходящимся.
называется
сходящимся. -
Если не существует конечного
 (
( или
или  ),
то интеграл
),
то интеграл  называется
расходящимся к
называется
расходящимся к  ,
или просто расходящимся.
,
или просто расходящимся.
Пусть ![]() определена
и непрерывна на множестве от
определена
и непрерывна на множестве от ![]() и
и  .
Тогда:
.
Тогда:
-
Если
 ,
то используется обозначение
,
то используется обозначение  и
интеграл называется несобственным
интегралом Римана первого рода. В
этом случае
и
интеграл называется несобственным
интегралом Римана первого рода. В
этом случае  называется
сходящимся.
называется
сходящимся. -
Если не существует конечного
 (
( или
или  ),
то интеграл
),
то интеграл  называется
расходящимся к
называется
расходящимся к  ,
или просто расходящимся.
,
или просто расходящимся.
Если
функция ![]() определена
и непрерывна на всей числовой прямой,
то может существовать несобственный
интеграл данной функции с двумя
бесконечными пределами интегрирования,
определяющийся формулой:
определена
и непрерывна на всей числовой прямой,
то может существовать несобственный
интеграл данной функции с двумя
бесконечными пределами интегрирования,
определяющийся формулой:
 ,
где с — произвольное число.
,
где с — произвольное число.
Геометрический смысл несобственного интеграла I родаНесобственный интеграл первого рода выражает площадь бесконечно длинной криволинейной трапеции.
Примеры
Несобственные
интегралы II родаПусть ![]() определена
на
определена
на ![]() ,
терпит бесконечный разрыв в точке x=a
и
,
терпит бесконечный разрыв в точке x=a
и  .
Тогда:
.
Тогда:
-
Если
 ,
то используется обозначение
,
то используется обозначение  и
интеграл называется несобственным
интегралом Римана второго рода. В
этом случае интеграл называется
сходящимся.
и
интеграл называется несобственным
интегралом Римана второго рода. В
этом случае интеграл называется
сходящимся. -
Если
 или
или  ,
то обозначение сохраняется, а
,
то обозначение сохраняется, а  называется
расходящимся к
называется
расходящимся к  ,
или просто расходящимся.
,
или просто расходящимся.
Пусть ![]() определена
на
определена
на ![]() ,
терпит бесконечный разрыв при x=b и
,
терпит бесконечный разрыв при x=b и  .
Тогда:
.
Тогда:
-
Если
 ,
то используется обозначение
,
то используется обозначение  и
интеграл называется несобственным
интегралом Римана второго рода. В
этом случае интеграл называется
сходящимся.
и
интеграл называется несобственным
интегралом Римана второго рода. В
этом случае интеграл называется
сходящимся. -
Если
 или
или  ,
то обозначение сохраняется, а
,
то обозначение сохраняется, а 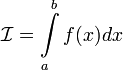 называется
расходящимся к
называется
расходящимся к  ,
или просто расходящимся.
,
или просто расходящимся.
Если
функция ![]() терпит
разрыв во внутренней точке
терпит
разрыв во внутренней точке ![]() отрезка
отрезка ![]() ,
то несобственный интеграл второго рода
определяется формулой:
,
то несобственный интеграл второго рода
определяется формулой:

Геометрический смысл несобственных интегралов II рода
Несобственный интеграл второго рода выражает площадь бесконечно высокой криволинейной трапеции
Пример
Отдельный
случайПусть функция ![]() определена
на всей числовой оси и имеет разрыв в
точках
определена
на всей числовой оси и имеет разрыв в
точках ![]() .
.
Тогда можно
найти несобственный интеграл 
Критерий
Коши1. Пусть ![]() определена
на множестве от
определена
на множестве от ![]() и
и  .
.
Тогда  сходится
сходится 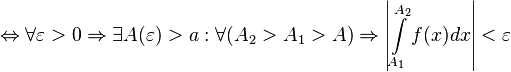
2.
Пусть ![]() определена
на
определена
на ![]() и
и  .
.
Тогда  сходится
сходится 
Абсолютная
сходимостьИнтеграл  называется абсолютно
сходящимся, если
называется абсолютно
сходящимся, если  сходится.
Если
интеграл сходится абсолютно, то он
сходится.
сходится.
Если
интеграл сходится абсолютно, то он
сходится.
Условная
сходимостьИнтеграл 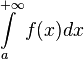 называется условно
сходящимся, если
называется условно
сходящимся, если  сходится,
а
сходится,
а  расходится.
расходится.
Первообразная
Первообрáзной[1] или примити́вной функцией (иногда называют также антипроизводной) данной функции f называют такую F, производная которой (на всей области определения) равна f, то есть F ′ = f. Вычисление первообразной заключается в нахождении неопределённого интеграла, а сам процесс называетсяинтегрированием.
Так, например,
функция ![]() является
первообразной
является
первообразной ![]() .
Так как производная константы равна нулю,
.
Так как производная константы равна нулю, ![]() будет
иметь бесконечное количество
первообразных, таких как
будет
иметь бесконечное количество
первообразных, таких как ![]() или
или ![]() … и
т. д.; таким образом семейство первообразных
функции
… и
т. д.; таким образом семейство первообразных
функции ![]() можно
обозначить как
можно
обозначить как ![]() ,
где C — любое число. Графики таких
первообразных смещены вертикально
относительно друг друга, и их положение
зависит от значения C.
,
где C — любое число. Графики таких
первообразных смещены вертикально
относительно друг друга, и их положение
зависит от значения C.
Первообразные важны тем, что позволяют вычислять интегралы. Если F — первообразная интегрируемой функции f, то:

Это соотношение называется формулой Ньютона — Лейбница.
Благодаря этой связи множество первообразных данной функции f называют неопределённым интегралом (общим интегралом) f и записывают в виде интеграла без указания пределов:
![]()
Если F — первообразная f, и функция f определена на каком-либо интервале, тогда каждая последующая первообразная G отличается от F на константу: всегда существует число C, такое что G(x) = F(x) + C для всех x. Число C называют постоянной интегрирования.
Каждая непрерывная функция f имеет первообразную F, одна из которых представляется в виде интеграла от f с переменным верхним пределом:

Также
существуют не непрерывные (разрывные)
функции, которые имеют первообразную.
Например, ![]() с
с ![]() не
непрерывна при
не
непрерывна при![]() ,
но имеет первообразную
,
но имеет первообразную ![]() с
с ![]() .
.
Некоторые первообразные, даже несмотря на то, что они существуют, не могут быть выражены через элементарные функции(такие как многочлены, экспоненциальные функции, логарифмы, тригонометрические функции, обратные тригонометрические функции и их комбинации). Например:
![]()
Более развёрнутое изложение этих фактов см. в дифференциальной теории Галуа.
Содержание
-
1 Свойства первообразной
-
2 Техника интегрирования
-
3 Другие определения
-
3.1 Определение первообразной через предел -ой производной
-
-
4 Примечания
-
5 Ссылки
-
6 См. также
Свойства первообразной
Первообразная суммы равна сумме первообразных
-
Первообразная произведения константы и функции равна произведению константы и первообразной функции
-
Достаточным условием существования первообразной у заданной на отрезке функции
 является
непрерывность
является
непрерывность 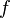 на
этом отрезке
на
этом отрезке -
Необходимыми условиями существования являются принадлежность функции
 первому классу
Бэра и выполнение для неё свойства
Дарбу
первому классу
Бэра и выполнение для неё свойства
Дарбу -
У заданной на отрезке функции любые две первообразные отличаются на постоянную.
Техника интегрирования
Основная статья: Методы интегрирования
Нахождение первообразных значительно сложнее, чем нахождение производных. Для этого имеется несколько методов:
-
линейность интегрирования позволяет разбивать сложные интегралы на части,
-
интегрирование через подстановку, часто применяемое вместе с тригонометрическими тождествами или натуральным логарифмом,
-
интегрирование по частям для операций с произведениями функций,
-
метод обратной цепочки, особый случай интегрирования по частям,
-
метод интегрирования рациональных дробей позволяет интегрировать любые рациональные функции (дроби с полиномами в числителе и знаменателе),
-
алгоритм Риша - алгоритм для интегрирования любых элементарных функций,
-
некоторые интегралы можно найти в таблице интегралов,
-
при многократном интегрировании можно использовать дополнительную технику, для примера см. двойной интеграл и полярные координаты, Якобиан и теорема Стокса,
-
Системы компьютерной алгебры помогают автоматизировать некоторые вышеприведённые символьные операции (в частности алгоритм Риша), что очень удобно, когда алгебраические вычисления становятся слишком громоздкими,
-
если функция не имеет элементарной первообразной (как, например,
 ),
её интеграл может быть вычислен
приближённо с помощью численного
интегрирования.
),
её интеграл может быть вычислен
приближённо с помощью численного
интегрирования.
Другие
определенияЭто определение является
наиболее распространенным, но встречаются
и другие, в которых ослаблены требования
существования всюду конечной ![]() и
выполнения всюду равенства
и
выполнения всюду равенства ![]() ,
иногда в определении используют обобщения
производной.
,
иногда в определении используют обобщения
производной.
Определение
первообразной через предел ![]() -ой
производнойФункция
-ой
производнойФункция ![]() называется
первообразной для функции
называется
первообразной для функции ![]() если
будет существовать предел для
функции
если
будет существовать предел для
функции ![]() являющейся
производной
являющейся
производной ![]() -го
порядка для функции
-го
порядка для функции ![]() то
есть
то
есть
![]()
Теорема. Данное определение эквивалентно основному определению.
В самом деле,
![]()
Пример
1. Вычислим первообразную для
функции ![]()
И так,
![]() при
условии, что
при
условии, что ![]()
Поскольку
![]()
Получаем
![]()
Пример
2. Вычислим первообразную для
функции ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Свойства интегралов
Это
свойство вполне очевидно, если
Однако
оно остается справедливым и в том
случае, когда
Выражение
|
Экстремум
Экстре́мум (лат. extremum — крайний) в математике — максимальное или минимальное значение функции на заданном множестве. Точка, в которой достигается экстремум, называется точкой экстремума. Соответственно, если достигается минимум — точка экстремума называется точкой минимума, а если максимум —точкой максимума. В математическом анализе выделяют также понятие локальный экстремум (соответственно минимум или максимум).
Содержание
-
1 Определения
-
2 Замечание
-
3 Необходимые условия существования локальных экстремумов
-
4 Достаточные условия существования локальных экстремумов
ОпределенияПусть
дана функция ![]() и
и ![]() —
внутренняя точка области определения
—
внутренняя точка области определения ![]() Тогда
Тогда
-
 называется
точкой локального максимума функции
называется
точкой локального максимума функции  если
существует проколотая окрестность
если
существует проколотая окрестность  такая,
что
такая,
что
![]()
-
 называется
точкой локального минимума функции
называется
точкой локального минимума функции  если
существует проколотая окрестность
если
существует проколотая окрестность  такая,
что
такая,
что
![]()
Если
неравенства выше строгие, то ![]() называется
точкой строгого локального максимума
или минимума соответственно.
называется
точкой строгого локального максимума
или минимума соответственно.
-
 называется
точкой абсолютного (глобального)
максимума, если
называется
точкой абсолютного (глобального)
максимума, если
![]()
-
 называется
точкой абсолютного минимума, если
называется
точкой абсолютного минимума, если
![]()
Значение
функции ![]() называют
(строгим) (локальным) максимумом или
минимумом в зависимости от ситуации.
Точки, являющиеся точками (локального)
максимума или минимума, называются
точками (локального) экстремума.
называют
(строгим) (локальным) максимумом или
минимумом в зависимости от ситуации.
Точки, являющиеся точками (локального)
максимума или минимума, называются
точками (локального) экстремума.
Замечание
Функция ![]() определённая
на множестве
определённая
на множестве ![]() может
не иметь на нём ни одного локального
или абсолютного экстремума. Например,
может
не иметь на нём ни одного локального
или абсолютного экстремума. Например, ![]()
Необходимые условия существования локальных экстремумов[править | править исходный текст]
-
Из леммы Ферма вытекает следующее:
Пусть
точка ![]() является
точкой экстремума функции
является
точкой экстремума функции ![]() ,
определенной в некоторой окрестности
точки
,
определенной в некоторой окрестности
точки ![]() .
.
Тогда либо
производная ![]() не
существует, либо
не
существует, либо ![]() .
.
(Математический Анализ. Том 1. Л. Д. Кудрявцев. Москва «Высшая Школа» 1973 г.)
Достаточные условия существования локальных экстремумов[править | править исходный текст]
-
Пусть функция
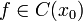 непрерывна
в
непрерывна
в  и
существуют конечные или бесконечные
односторонние производные
и
существуют конечные или бесконечные
односторонние производные  .
Тогда при условии
.
Тогда при условии
![]()
![]() является
точкой строгого локального максимума.
А если
является
точкой строгого локального максимума.
А если
![]()
то ![]() является
точкой строгого локального минимума.
является
точкой строгого локального минимума.
Заметим,
что при этом функция не дифференцируема
в точке ![]()
-
Пусть функция
 непрерывна
и дважды дифференцируема в точке
непрерывна
и дважды дифференцируема в точке  .
Тогда при условии
.
Тогда при условии
![]() и
и ![]()
![]() является
точкой локального максимума. А если
является
точкой локального максимума. А если
![]() и
и ![]()
то ![]() является
точкой локального минимума.
является
точкой локального минимума.
-
Пусть функция
 дифференцируема
дифференцируема  раз
в точке
раз
в точке  и
и  ,
а
,
а  .
.
Если ![]() чётно
и
чётно
и ![]() ,
то
,
то ![]() -
точка локального максимума. Если
-
точка локального максимума. Если ![]() чётно
и
чётно
и ![]() ,
то
,
то ![]() -
точка локального минимума. Если
-
точка локального минимума. Если ![]() нечётно,
то экстремума нет.
нечётно,
то экстремума нет.
Параграф 4.Экстремумы функции.
Определение 1. Говорят, что в точке функция имеет локальный максимум (локальный минимум), если .
В этом определении обратите внимание на слово “локальный”. Оно означает, что принимает свое наибольшее значение в точке только по отношению к отрезку . Вне этого отрезка о поведении функции ничего не утверждается: она может принять там и значение, большее чем . То же самое можно сказать и по отн. к локальному минимуму.
Определене 2.Говорят, что функция имеет в точке глобальный максимум (минимум) на множестве если .
Термины “максимум” и “минимум” объединяют одним словом “экстремум” и говорят о локальном или глобальном экстремуме. Отметьте еще, что для непрерывной функции локальный максимумы или минимумы чередуются.
Нахождение локальных экстремумов - одна из важнейших задач исследования функций имеющая большое практическое значение. Перейдем к е изучению.
Пусть функция FO определена на некотором отрезке . Научимся сначала находить локальные экстремумы, расположенные внутри этого отрезка.
Необходимое условие экстремума
Пусть в точке , такой, что , функция принимает свое экстремальное, т.е. наибольшее или наименьшее значение. Тогда по теореме Ферма
Это и дает необходимое условие экстремума. Отметьте, что если выполнено условие то это еще не означает, что в точке функция имеет локальный экстремум. Условие дает лишь точку “подозрительную” на экстремум, и что там на самом деле, - еще предстоит ответить.
Итак, пусть в некоторой точке выполняется условие Достаточное условие экстремума , т.е. эта точка является “подозрительной” на экстремум. Что же на самом деле в этой точке?
Для дальнейшего основным для нас будет разложение функции в ряд Тейлора с остаточным членом в форме Пеано
*
и тот факт, что из-за условия второе слагаемое в этом разложении исчезает.
Разберем основные случаи в порядке их усложнения.
А. Пусть . тогда разложение (*) принимает вид
Функция - это парабола. График в окрестности точки в зависимости от знака изображен на рисунках
Из рисунков
видно, что если < то в точке -
локальный минимум, а если , то в -
локальный максимум. Б. Пусть но .
Тогда разложение (*) примет вид
График функции в окрестности точке имеет вид

<Отсюда видно, что экстремума в точке нет.
В. Пусть но
. Тогда
График функции напоминает параболу. Поэтому график в окрестности точки имеет вид

Отсюда видно, что если то в точке - локальный минимум, а если, то в точке - локальный максимум.
Г. Пусть но. тогда Так как - нечетное число, то график напоминает график функции . Поэтому график в окрестности точки имеет вид
Отсюда
видно, что в точке экстремума нет.
Случай, когда в точке существуют лишь односторонние производные
На теорему Ферма можно ссылаться лишь тогда, когда в точке. Если же не существует, то теорема Ферма не работает. Рассмотрим случай, когда в точке существуют лишь односторонние производные и. Вспомним, что производная - это тангенс угла наклона касательной к оси OY, будем иметь следующие четыре варианта
Глобальный минимум
Материал из свободной русской энциклопедии «Традиция». Вы можете дополнить или исправить его.
Глобальный минимум (абсолютный минимум) — минимум (точка минимума), наблюдающийся на всей области определения функции. Глобальный минимум является минимальным среди всех локальных минимумов функции.
Определение[править]
Пусть дана функция , и x0∈M0 — внутренняя точка области определения f. Тогда x0 называется точкой локального минимума функции f, если существует проколотая окрестность U˙(x0) такая, что
∀x∈Mf(x)⩾f(x0).
Данное определение может быть распространено на произвольные функции, для типов результатов которых имеют смысл операции сравнения (>) и (⩾).

Отсюда видно, что если и имеют разные знаки, то в точке - локальный экстремум. Если и имеют одинаковые знаки, то локального экстремума нет.
Граничные точки
Рассмотрим
наконец, граничные точки a и b отрезка .
Здесь поведение функции может быть
следующим.
Таким образом, что мы имеем в граничных точках, определяется знаком первой производной.
Подведем итоги.
Схема исследования функции на экстремумы
Чтобы исследовать экстремумы функции надо сделать следующее:
1. Найти те точки , в которых . Это будут точки, “подозрительные” на наличие в них экстремума.
2. В точках где найти первую по порядку старшинства производную, отличную от нуля. Если это будет производная четного порядка - в точке локальный экстремум (если эта производная отрицательная - то максимум, если положительная - то минимум), если же нечетного порядка - в точке экстремума нет.
3. Найти те точки, где существуют лишь односторонние производные. Если эти производные разных знаков - в точке локальный экстремум, если одного знака - экстремума нет.
4. Найти производные на границах области задания функции и определить, как ведет себя функция на границе.
5. Вычислить значения функции в точках локальных минимумов и максимумов и найти глобальный минимум (наименьший из локальных минимумов) и глобальный максимум (наибольший из локальных максимумов).
Глобальный максимум (абсолютный максимум) — максимум (точка максимума), наблюдающийся на всей области определения функции. Глобальный максимум является максимальным среди всех локальных максимумов функции.
Определение[править]
Пусть дана функция Undefined control sequence \R, и x0∈M0 — внутренняя точка области определения f. Тогда x0 называется точкой локального минимума функции f, если существует проколотая окрестность U˙(x0) такая, что
∀x∈Mf(x)⩽f(x0).
Данное определение может быть распространено на произвольные функции, для типов результатов которых имеют смысл операции сравнения () и (⩽).
Экстремум (лат. extremum — крайний) в математике — максимальное или минимальное значение функции на заданном множестве. Точка, в которой достигается экстремум называется точкой экстремума. Соответственно, если достигается минимум — точка экстремума называется точкой минимума, а если максимум — точкой максимума. В математическом анализе выделяют также понятие локальный экстремум и глобальный экстремум.
Интеграл. Свойства неопределённого интеграла, методы нахождения
Первообразная функция и неопределённый интеграл
Свойства неопределённого интеграла
Таблица основных неопределённых интегралов
Метод разложения
Метод подстановки
Метод интегрирования по частям
Первообразная функция и неопределённый интеграл
Задачей дифференциального исчисления являлось нахождение для каждой функции её производной. Поставим обратную задачу: для данной функции f(x) найти такую функцию F(x), производная которой равна f(x). Например, для функции
![]()
этому условию удовлетворяет функция
![]()
так как
![]()
|
|
К пониманию |
|
Это одна из типичных задач об обратной операции, которые очень часто встречаются в математике. Так, например, ещё в элементарной математике задача об умножении поставила обратную задачу о делении, задача возведения в степень вызвала обратную задачу извлечения корня и т.д. Точно так же задача дифференцирования ставит обратную задачу об отыскании функции по её производной. |
|
Функция F(x) называется первообразной для функции f(x), если производная F(x) равна f(x), или, что одно и то же, дифференциал F(x) равен f(x) dx, т.е.
![]()
или
![]() (1)
(1)
Следовательно,
функция ![]() -
первообразная для функции
-
первообразная для функции ![]() .
Однако она не является единственной
первообразной для
.
Однако она не является единственной
первообразной для ![]() .
Ими служат также функции
.
Ими служат также функции

и вообще
![]()
где С –
произвольная постоянная. В этом можно
убедиться дифференцированием. Таким
образом, если для функции существует
одна первообразная, то для неё существует
бесконечное множество первообразных,
отличающихся на постоянное слагаемое.
Все первообразные для функции ![]() записываются
в приведённом выше виде. Это вытекает
из следующей теоремы.
записываются
в приведённом выше виде. Это вытекает
из следующей теоремы.
Теорема. Если F(x) – первообразная для функции f(x) на некотором промежутке Х, то любая другая первообразная для f(x) на том же промежутке может быть представлена в виде F(x) + C , где С – произвольная постоянная.
Неопределённым интегралом функции f(x) называется совокупность всех её первообразных. При этом употребляется запись
![]() где
знак
где
знак ![]() называется
знаком интеграла, функция f(x)
– подынтегральной функцией, а f(x)dx –
подынтегральным выражением.
называется
знаком интеграла, функция f(x)
– подынтегральной функцией, а f(x)dx –
подынтегральным выражением.
Таким образом, если F(x) – какая-нибудь первообразная для f(x) , то
![]() (2)
(2)
Процесс нахождения неопределённого интеграла функции называется интегрированием этой функции.
Свойства неопределённого интеграла
Теорема 1. Производная неопределённого интеграла равна подынтегральной функции, а его дифференциал – подынтегральному выражению.
Теорема 2. Неопределённый интеграл от дифференциала функции f(x) равен функции f(x) с точностью до постоянного слагаемого, т.е.
![]() (3)
(3)
Теоремы 1 и 2 показывают, что дифференцирование и интегрирование являются взаимно-обратными операциями.
Теорема 3. Постоянный множитель в подынтегральном выражении можно выносить за знак неопределённого интеграла, т.е.
![]() (4)
(4)
Теорема 4. Неопределённый интеграл алгебраической суммы конечного числа функций равен алгебраической сумме неопределённых интегралов этих функций, т.е.
![]() (5)
(5)
Таблица основных неопределённых интегралов
Из определения неопределённого интеграла вытекают следующие формулы, которые в дальнейшем будем называть табличными интегралами:
![]() (6)
(6)
![]() (7)
(7)
![]() (8)
(8)
![]() (9)
(9)
![]() (10)
(10)
![]() (11)
(11)
![]() (12)
(12)
![]() (13)
(13)
![]() (14)
(14)
![]() (15)
(15)
Пример 1. Найти:
1) ![]()
2) ![]()
3) ![]()
Решение.
1) Применяя формулу (6) при n = 3, получим
![]()
2) Используя снова формулу (7) при n = 1/3, имеем
![]()
3) Так как
![]()
то по формуле (6) при n = -1/4 найдём
![]()
Метод разложения
Метод разложения состоит в использовании при интегрировании теорем 3 и 4 из параграфа «Свойства неопределённого интеграла». Проиллюстрируем применение этого метода на примерах.
Пример 2. Найти
![]()
Решение. Применяя сначала теорему 4, а затем теорему 3 параграфа «Свойства неопределённого интеграла», найдём
![]()
Все три полученные интеграла – табличные. Используя формулу (6) при n = 1/2, n = 2 и n = 1/5, имеем

где
![]()
объединяет все три произвольные постоянные, которые были введены при нахождении трёх интегралов. Поэтому в аналогичных ситуациях следует вводить только одну произвольную постоянную.
Пример 3. Найти
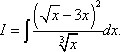
Решение. Сначала преобразуем подынтегральную функцию. Возведя двучлен в квадрат и разделив почленно числитель на знаменатель, получим
![]()
(затем мы применили теоремы 4 и 3 параграфа «Свойства неопределённых интегралов»). Все полученные интегралы – табличные. Используя формулу (6) при n = 2/3, n = 7/6, n = 5/3, найдём

Пример 4. Найти
![]()
Решение. Представим числитель подынтегральной функции, равный 1, в виде
![]()
Тогда
 Оба
интеграла – табличные. Используя формулы
(12) и (13), получим
Оба
интеграла – табличные. Используя формулы
(12) и (13), получим
![]()
Метод подстановки
Во многих случаях введение новой переменной интегрирования позволяет свести нахождение данного интеграла к нахождению табличного интеграла. Такой метод называется методом подстановки илиметодом замены переменной. Он основан на следующей теореме.
Теорема. Пусть
функция ![]() определена
и дифференцируема на некотором
промежутке Т и пусть Х –
множество значений этой функции, на
котором определена функция f(x).
Тогда, если на множестве Хфункция f(x)
имеет первообразную, то на
множестве Т справедлива формула
определена
и дифференцируема на некотором
промежутке Т и пусть Х –
множество значений этой функции, на
котором определена функция f(x).
Тогда, если на множестве Хфункция f(x)
имеет первообразную, то на
множестве Т справедлива формула
![]() (16)
(16)
Формула (16) называется формулой замены переменной в неопределённом интеграле.
Пример 5. Вычислить интеграл
![]()
Решение. Положим x – 1 = t ; тогда x = t + 1. Отсюда dx = dt . По формуле (16)
![]()
Возвращаясь к переменной x, окончательно получаем
![]()
Замечание. При замене переменной в неопределённом интеграле иногда более удобно задавать не х как функцию t, а, наоборот, задавать t как функцию от x.
Заметим, что удачный выбор подстановки обычно представляет известные трудности. Для их преодоления необходимо овладеть техникой дифференцирования и хорошо знать табличные интегралы.
Метод интегрирования по частям
Метод интегрирования по частям основан на использовании формулы дифференцирования произведения двух функций.
Теорема. Пусть функции u(x) и v(x) определены и дифференцируемы на некотором промежутке Х и пусть функция
![]()
имеет первообразную на этом промежутке. Тогда на промежутке Х функция
![]()
также имеет первообразную и справедлива формула
![]() (17)
(17)
Формула (17) называется формулой интегрирования по частям в неопределённом интеграле.
Так как
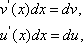
то её можно записать в виде
![]()
Пример 6. Вычислить
![]() Решение.
Полагая, что
Решение.
Полагая, что

находим
![]()
Предел функции
|
|
|
|
1 |
0.841471 |
|
0.1 |
0.998334 |
|
0.01 |
0.999983 |
Хотя
функция ![]() в
нуле не определена, когда
в
нуле не определена, когда ![]() приближается
к нулю, но её значение становится сколь
угодно близко к 1 в окрестности нуля,
иными словами — предел функции в
нуле равен 1.
приближается
к нулю, но её значение становится сколь
угодно близко к 1 в окрестности нуля,
иными словами — предел функции в
нуле равен 1.
У этого термина существуют и другие значения, см. Предел.

![]()
График
функции, предел которой при аргументе,
стремящемся к бесконечности, равен ![]() .
.
Преде́л фу́нкции (предельное значение функции) в заданной точке, предельной для области определения функции, — такая величина, к которой стремится рассматриваемая функция при стремлении её аргумента к данной точке.
Предел функции является обобщением понятия предела последовательности: изначально под пределом функции в точке понимали предел последовательности элементов области значений функции, составленной из образов точек последовательности элементов области определения функции, сходящейся к заданной точке (предел в которой рассматривается); если такой предел существует, то говорят, что функция сходится к указанному значению; если такого предела не существует, то говорят, что функция расходится.
Наиболее часто определение предела функции формулируют на языке окрестностей. То, что предел функции рассматривается только в точках, предельных для области определения функции, означает, что в каждой окрестности данной точки есть точки области определения; это позволяет говорить о стремлении аргумента функции (к данной точке). Но предельная точка области определения не обязана принадлежать самой области определения: например, можно рассматривать предел функции на концах открытого интервала, на котором определена функция (сами концы интервала в область определения не входят).
В общем случае необходимо точно указывать способ сходимости функции, для чего вводят т.н. базу подмножествобласти определения функции, и тогда формулируют определение предела функции по (заданной) базе. В этом смысле система проколотых окрестностей данной точки — частный случай такой базы множеств.
Поскольку на расширенной вещественной прямой можно построить базу окрестностей бесконечно удалённой точки, то оказывается допустимым описание предела функции при стремлении аргумента к бесконечности, а также описание ситуации, когда функция сама стремится к бесконечности (в заданной точке). Предел последовательности (как предел функции натурального аргумента), как раз предоставляет пример сходимости по базе «стремление аргумента к бесконечности».
Отсутствие предела функции (в данной точке) означает, что для любого заранее заданного значения области значений и всякой его окрестности сколь угодно близко от заданной точки существуют точки, значение функции в которых окажется за пределами заданной окрестности.
Если в некоторой точке области определения функции существует предел и этот предел равен значению функции в данной точке, то функция оказывается непрерывной(в данной точке).
Предел фу́нкции — одно из основных понятий математического анализа.
Содержание
1 Определения
-
1.1 Предел функции по Гейне
-
1.2 Предел функции по Коши
-
1.3 Окрестностное определение предела по Коши
-
1.4 Предел по базе множеств
-
1.5 Эквивалентность определений
-
2 Вариации и обобщения
-
2.1 Односторонний предел
-
2.2 Предел вдоль фильтра
-
2.3 Пределы на бесконечности
-
2.3.1 Предел на бесконечности по Гейне
-
2.3.2 Предел на бесконечности по Коши
-
2.3.3 Окрестностное определение по Коши
-
-
-
3 Обозначения
-
4 Свойства пределов числовых функций
-
5 Примеры
-
6 См. также
-
7 Примечания
-
8 Литература
Определения[править | править исходный текст]
Рассмотрим функцию ![]() ,
определённую на некотором множестве
,
определённую на некотором множестве ![]() ,
которое имеет предельную
точку
,
которое имеет предельную
точку ![]() (которая,
в свою очередь, не обязана ему принадлежать).
(которая,
в свою очередь, не обязана ему принадлежать).
Предел функции по Гейне[править | править исходный текст]
Значение ![]() называется пределом (предельным
значением) функции
называется пределом (предельным
значением) функции ![]() в
точке
в
точке ![]() ,
если для любой последовательности точек
,
если для любой последовательности точек ![]() ,
сходящейся к
,
сходящейся к ![]() ,
но не содержащей
,
но не содержащей ![]() в
качестве одного из своих элементов (то
есть в проколотой окрестности
в
качестве одного из своих элементов (то
есть в проколотой окрестности ![]() ),
последовательность значений
функции
),
последовательность значений
функции ![]() сходится
к
сходится
к![]() .[1]
.[1]
![]()
Предел функции по Коши[править | править исходный текст]
Значение ![]() называется пределом (предельным
значением) функции
называется пределом (предельным
значением) функции ![]() в
точке
в
точке ![]() ,
если для любого наперёд взятого
положительного числа
,
если для любого наперёд взятого
положительного числа ![]() найдётся
отвечающее ему положительное число
найдётся
отвечающее ему положительное число ![]() такое,
что для всех аргументов
такое,
что для всех аргументов ![]() ,
удовлетворяющих условию
,
удовлетворяющих условию ![]() ,
выполняется неравенство
,
выполняется неравенство ![]() .[1]
.[1]
![]()
Окрестностное определение предела по Коши[править | править исходный текст]
Значение ![]() называется пределом (предельным
значением) функции
называется пределом (предельным
значением) функции ![]() в
точке
в
точке ![]() ,
если для любой окрестности
,
если для любой окрестности ![]() точки
точки ![]() существует
выколотая окрестность
существует
выколотая окрестность ![]() точки
точки ![]() такая,
что образ этой окрестности
такая,
что образ этой окрестности ![]() лежит
в
лежит
в ![]() .
Фундаментальное обоснование данного
определения предела можно найти в
статье Предел
вдоль фильтра.
.
Фундаментальное обоснование данного
определения предела можно найти в
статье Предел
вдоль фильтра.
![]()
Предел по базе множеств[править | править исходный текст]
Наиболее общим определением является определение предела функции по базе (по базису фильтра, по фильтру).
Пусть ![]() —
некоторая база
подмножеств области определения.
Тогда
—
некоторая база
подмножеств области определения.
Тогда
-
число
 называется
пределом функции по (при) базе
называется
пределом функции по (при) базе  ,
если для всякого
,
если для всякого 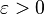 найдётся
такой элемент
найдётся
такой элемент  базы,
что для любого
базы,
что для любого  выполнено
выполнено  .
.
Если ![]() — предельная
точка множества
— предельная
точка множества ![]() ,
то это означает, что каждая проколотая
окрестность точки в множестве
,
то это означает, что каждая проколотая
окрестность точки в множестве ![]() не
пуста, а, значит, существует база проколотых
окрестностей в точке
не
пуста, а, значит, существует база проколотых
окрестностей в точке ![]() .
Эта база имеет специальное обозначение
«
.
Эта база имеет специальное обозначение
«![]() »
и читается «при
»
и читается «при ![]() ,
стремящемся к
,
стремящемся к ![]() по
множеству
по
множеству ![]() ».
Если область определения функции
».
Если область определения функции ![]() совпадает
с
совпадает
с ![]() ,
то значок множества опускается, тогда
база обозначается совсем просто «
,
то значок множества опускается, тогда
база обозначается совсем просто «![]() »
и читается «при
»
и читается «при ![]() ,
стремящемся к
,
стремящемся к ![]() ».
».
При рассмотрении только числовых функций вещественного переменного также рассматриваются и базы односторонних окрестностей. Для этого рассматриваются два множества:
-
 ,
где
,
где  ;
; -
 ,
где
,
где  .
.
Соответственно этому вводятся две базы:
-
«
 »,
которая коротко обозначается в виде
«
»,
которая коротко обозначается в виде
« »
или ещё проще «
»
или ещё проще « »;
»; -
«
 »,
которая коротко обозначается в виде
«
»,
которая коротко обозначается в виде
« »
или ещё проще «
»
или ещё проще « ».
».
Эквивалентность определений[править | править исходный текст]
Все данные выше определения предела функции в точке эквивалентны.[1] Иными словами, из любого из них можно вывести любое другое, то есть выполнение одного из них неизбежно влечёт выполнение всех остальных.
Вариации и обобщения[править | править исходный текст]
Односторонний предел[править | править исходный текст]
Основная статья: Односторонний предел
Односторонний предел числовой функции в точке — это специфический предел, подразумевающий, что аргумент функции приближается к указанной точке с определённой стороны (слева или справа). Числовая функция имеет предел в точке тогда и только тогда, когда она имеет в этой точке совпадающие левый и правый пределы.
Предел вдоль фильтра[править | править исходный текст]
Основная статья: Предел вдоль фильтра
Предел функции вдоль фильтра — это обобщение понятия предела на случай произвольной области определения функции. Задавая частные случаи области определения и базиса фильтра на ней, можно получить многие приведённые в этой статье определения пределов.
Пределы на бесконечности[править | править исходный текст]
Предел функции на бесконечности описывает поведение значения данной функции, когда её аргумент становится бесконечно большим. Существуют различные определения таких пределов, но они эквивалентны между собой.
Предел на бесконечности по Гейне[править | править исходный текст]
-
Пусть числовая функция
 задана
на множестве
задана
на множестве  ,
в котором отыщется сколь угодно большой
элемент, то есть для всякого
положительного
,
в котором отыщется сколь угодно большой
элемент, то есть для всякого
положительного  в
нём найдётся элемент, лежащий за
границами отрезка
в
нём найдётся элемент, лежащий за
границами отрезка  .
В этом случае число
.
В этом случае число  называется
пределом функции
называется
пределом функции  на
бесконечности, если для всякой
бесконечно
большой последовательности точек
на
бесконечности, если для всякой
бесконечно
большой последовательности точек  соответствующая
последовательность частных значений
функции в этих точках
соответствующая
последовательность частных значений
функции в этих точках  сходится
к числу
сходится
к числу  .
.
![]()
-
Пусть числовая функция
 задана
на множестве
задана
на множестве  ,
в котором для любого числа
,
в котором для любого числа  найдётся
элемент, лежащий правее него. В этом
случае число
найдётся
элемент, лежащий правее него. В этом
случае число  называется
пределом функции
называется
пределом функции  на
плюс бесконечности, если для всякой
бесконечно большой последовательности
положительных точек
на
плюс бесконечности, если для всякой
бесконечно большой последовательности
положительных точек  соответствующая
последовательность частных значений
функции в этих точках
соответствующая
последовательность частных значений
функции в этих точках  сходится
к числу
сходится
к числу  .
.
![]()
-
Пусть числовая функция
 задана
на множестве
задана
на множестве  ,
в котором для любого числа
,
в котором для любого числа  найдётся
элемент, лежащий левее него. В этом
случае число
найдётся
элемент, лежащий левее него. В этом
случае число  называется
пределом функции
называется
пределом функции  на
минус бесконечности, если для всякой
бесконечно большой последовательности
отрицательных точек
на
минус бесконечности, если для всякой
бесконечно большой последовательности
отрицательных точек  соответствующая
последовательность частных значений
функции в этих точках
соответствующая
последовательность частных значений
функции в этих точках  сходится
к числу
сходится
к числу  .
.
![]()
Предел на бесконечности по Коши[править | править исходный текст]
-
Пусть числовая функция
 задана
на множестве
задана
на множестве  ,
в котором отыщется сколь угодно большой
элемент, то есть для всякого
положительного
,
в котором отыщется сколь угодно большой
элемент, то есть для всякого
положительного  в
нём найдётся элемент, лежащий за
границами отрезка
в
нём найдётся элемент, лежащий за
границами отрезка  .
В этом случае число
.
В этом случае число  называется
пределом функции
называется
пределом функции  на
бесконечности, если для произвольного
положительного числа
на
бесконечности, если для произвольного
положительного числа  отыщется
отвечающее ему положительное
число
отыщется
отвечающее ему положительное
число  такое,
что для всех точек, превышающих
такое,
что для всех точек, превышающих  по абсолютному
значению, справедливо неравенство
по абсолютному
значению, справедливо неравенство  .
.
![]()
-
Пусть числовая функция
 задана
на множестве
задана
на множестве  ,
в котором для любого числа
,
в котором для любого числа  найдётся
элемент, лежащий правее него. В этом
случае число
найдётся
элемент, лежащий правее него. В этом
случае число  называется
пределом функции
называется
пределом функции  на
плюс бесконечности, если для
произвольного положительного
числа
на
плюс бесконечности, если для
произвольного положительного
числа  отыщется
отвечающее ему положительное
число
отыщется
отвечающее ему положительное
число  такое,
что для всех точек, лежащих правее
такое,
что для всех точек, лежащих правее  ,
справедливо неравенство
,
справедливо неравенство  .
.
![]()
-
Пусть числовая функция
 задана
на множестве
задана
на множестве  ,
в котором для любого числа
,
в котором для любого числа  найдётся
элемент, лежащий левее него. В этом
случае число
найдётся
элемент, лежащий левее него. В этом
случае число  называется
пределом функции
называется
пределом функции  на
минус бесконечности, если для
произвольного положительного
числа
на
минус бесконечности, если для
произвольного положительного
числа  отыщется
отвечающее ему положительное
число
отыщется
отвечающее ему положительное
число  такое,
что для всех точек, лежащих левее
такое,
что для всех точек, лежащих левее  ,
справедливо неравенство
,
справедливо неравенство  .
.
![]()
Окрестностное определение по Коши[править | править исходный текст]
Пусть
функция ![]() определена
на множестве
определена
на множестве ![]() ,
имеющем элементы вне любой окрестности нуля.
В этом случае точка
,
имеющем элементы вне любой окрестности нуля.
В этом случае точка ![]() называется
пределом функции
называется
пределом функции ![]() на
бесконечности, если для любой её малой
окрестности найдётся достаточно большая
окрестность нуля, что значения функции
в точках, лежащих вне этой окрестности
нуля, попадают в эту окрестность точки
на
бесконечности, если для любой её малой
окрестности найдётся достаточно большая
окрестность нуля, что значения функции
в точках, лежащих вне этой окрестности
нуля, попадают в эту окрестность точки ![]() .
.
![]()
Обозначения[править | править исходный текст]
Если в
точке ![]() у
функции
у
функции ![]() существует
предел, равный
существует
предел, равный ![]() ,
то говорят, что функция
,
то говорят, что функция ![]() стремится к
стремится к ![]() при
стремлении
при
стремлении ![]() к
к ![]() ,
и пишут одним из следующих способов:
,
и пишут одним из следующих способов:
-
 ,
или
,
или -
 .
.
Если у
функции ![]() существует
предел на бесконечности,
равный
существует
предел на бесконечности,
равный ![]() ,
то говорят, что функция
,
то говорят, что функция ![]() стремится к
стремится к ![]() при
стремлении
при
стремлении ![]() к
бесконечности, и пишут одним из следующих
способов:
к
бесконечности, и пишут одним из следующих
способов:
-
 ,
или
,
или -
 .
.
Если у
функции ![]() существует
предел на плюс бесконечности, равный
существует
предел на плюс бесконечности, равный ![]() ,
то говорят, что функция
,
то говорят, что функция ![]() стремится к
стремится к ![]() при
стремлении
при
стремлении ![]() к
плюс бесконечности, и пишут одним из
следующих способов:
к
плюс бесконечности, и пишут одним из
следующих способов:
-
 ,
или
,
или -
 .
.
Если у
функции ![]() существует
предел на минус бесконечности, равный
существует
предел на минус бесконечности, равный ![]() ,
то говорят, что функция
,
то говорят, что функция ![]() стремится к
стремится к ![]() при
стремлении
при
стремлении ![]() к
минус бесконечности, и пишут одним из
следующих способов:
к
минус бесконечности, и пишут одним из
следующих способов:
-
 ,
или
,
или -
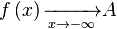 .
.
Свойства пределов числовых функций[править | править исходный текст]
Пусть даны
функции ![]() и
и ![]() .
.
-
Одна и та же функция в одной и той же точке может иметь только один предел.
![]()
Доказательство [показать]
-
Сходящаяся функция локально сохраняет знак. Более обще,
![]()
где ![]() —
проколотая окрестность точки
—
проколотая окрестность точки ![]() .
.
-
В частности, функция, сходящаяся к положительному (отрицательному) пределу, остаётся положительной (отрицательной) в некоторой окрестности предельной точки:
![]()
-
Сходящаяся функция локально ограничена в окрестности предельной точки:
![]()
-
Отделимость от нуля функций, имеющих предел, отличный от нуля.
![]()
-
Операция взятия предела сохраняет нестрогие неравенства.
![]()
-
Правило двух милиционеров
-
Предел суммы равен сумме пределов:
![]()
-
Предел разности равен разности пределов:
![]()
-
Предел произведения равен произведению пределов:
![]()
-
Предел частного равен частному пределов.

Примеры[править | править исходный текст]
-
Функция, возвращающая константу, имеет предел в любой точке, в которой определена. Он равен этой константе.
![]()
-
Тождественная функция в любой точке, в которой определена, имеет предел равный этой точке.
![]()
-
Функция Дирихле не имеет предела ни в какой точке числовой прямой.
![]()
-
Функция
 имеет
предел на бесконечности,
равный нулю.
имеет
предел на бесконечности,
равный нулю.
![]()
-
Функция арктангенс имеет на плюс и минус бесконечности пределы плюс и минус пи пополам соответственно и, следовательно, не имеет предела на бесконечности.
![]()
![]()
![]()
Пределы функций. Примеры решений
Теория пределов – это один из разделов математического анализа. Вопрос решения пределов является достаточно обширным, поскольку существуют десятки приемов решений пределов различных видов. Существуют десятки нюансов и хитростей, позволяющих решить тот или иной предел. Тем не менее, мы все-таки попробуем разобраться в основных типах пределов, которые наиболее часто встречаются на практике.
Начнем с самого понятия предела. Но сначала краткая историческая справка. Жил-был в 19 веке француз Огюстен Луи Коши, который заложил основы математического анализа и дал строгие определения, определение предела, в частности. Надо сказать, этот самый Коши снился, снится и будет сниться в кошмарных снах всем студентам физико-математических факультетов, так как доказал огромное количество теорем математического анализа, причем одна теорема отвратительнее другой. В этой связи мы не будем рассматривать строгое определение предела, а попытаемся сделать две вещи:

 .
.










 .
.

 .
.

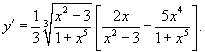







 Рис.
1.
Свойство 6 (случай
Рис.
1.
Свойство 6 (случай  Рис.
2.
Свойство 6 (случай
Рис.
2.
Свойство 6 (случай 



 называется средним
значением функции f(x)
на промежутке [a,b].
Поэтому свойство 8 называют теоремой
о среднем.
называется средним
значением функции f(x)
на промежутке [a,b].
Поэтому свойство 8 называют теоремой
о среднем.
 Рис.
3.
Площадь под кривой y = f(x)
на интервале [a,b]
равна площади прямоугольника с
основанием (b-a)
и высотой
Рис.
3.
Площадь под кривой y = f(x)
на интервале [a,b]
равна площади прямоугольника с
основанием (b-a)
и высотой 