kryl_vych_seti

матриц D, (т. е. матриц величин первого			1, второго 2 и т. д. кратчай-
ших путей). Каждый элемент матрицы			= ||δi,j|| имеет вид
δi, j = min		(γi,1 + d1,i );(γi,2 + d2, j );...(γi,i + di, j );...(γi,N + dN , j )			. (5.8)
k

В выражении (5.8) min означает, что минимум может браться для кратчайшего пути (к = 1), второго по длине пути (к = 2) и т. д. Каждый из членов (γi,ε + dε, j) = ∞ в выражении (5.8) определяет длину пути от узла i к узлу j, если первым транзитным узлом после узла i на пути к узлу j будет узел ε, ε (1, …, N). Если узел ε не является соседним узлом i, то

(γi,ε + dε,j) = ∞.

Так как γi,i = ∞, член (γi,i + di,j) будет всегда ∞. При этом элемент (γi,j +dj,j) не обязательно равен ∞. Таким образом, число членов выра-

жения (5.8), не равных бесконечности, равно числу n соседних УК, т. е. числу исходящих из УК направлений (ветвей).

Член выражения (5.8), имеющий минимальное значение и определяющий длину кратчайшего пути от узла i к узлу j через узел ε:

δ1	= min		(γ	i,1	+d	);...(γ	i,N	+d	N , j	)
i, j	1				1, j

заносится в качестве элемента δ1i, j в дисперсионную матрицу первого

выбора 1 = δ1i, j . Второй по значению член выражения (5.8), опреде-

ляющий длину второго по протяженности пути после кратчайшего от узла i к узлу j

δ2

= min

(γ

i,1

+d

);...(γ

i,N

+d

N , j

)

i, j

2

1, j

заносится в качестве элемента δi2, j

в дисперсионную матрицу второго

выбора 2 =

δi2, j

.

При наличии n соседних узлов можно получить n дисперсионных матриц 1,…, n.

Рассмотрим пример расчета элементов матриц ( 1, 2, …). Пусть сеть связи имеет вид, изображенный на рис. 5.2.

Тогда матрицы L1 и Г имеют следующий вид:

101

																																	A							B	C	D	E	F
A																																								30	∞	20	∞	∞
B																																							∞	0	15	20	∞	∞
L1 = C																																						∞ 15 0 20 25 ∞																							.
D																														20										15	20	0	∞	40
E																																							∞	∞	25	15	0	40
F																																	15							∞	∞	25	40	0
																						A																		B	C	D	E	F
A																																	∞							30	∞	20	∞	∞
B																																	∞							∞	15	20	∞	∞
Г = C																																	∞							15	∞	20	25	∞										.
D																	20																							15	20	∞	∞	40
E																																	∞							∞	25	15	∞	40
F																						15																		∞	∞	25	40	∞
Матрица D, вычисленная ранее, имеет вид
																												A												B	C	D	E	F
A																																						0		30	40	20	65	45
B																								35																0	15	15	40	40
D = C																					40																			15	0	20	25	45																				.
D																					20																			15	20	0	45	25
E																							30																	25	25	10	0	35
F																												15												40	45	25	40	0

Тогда, например, элемент δ1			,определяющий минимальный по про-
		1,2
тяженности путь от вершины A к вершине B матрицы							1 согласно (5.8):
δ1	= min[(γ	+d	);(γ	+d	2,2	);(γ +d	3,2	);
1,2	1,1	1,2	1,2			1,3
	1

102

(γ1,4 +d4,2 );(γ1,5 +d5,2 );(γ1,6 +d6,2 )] =

= min[(∞+30);(30 +0);(∞+15);(20 +15);(∞+ 25);(∞+ 40) = 30 .

1

Так как минимальное значение в выражении находится на втором месте, что соответствует вершине B, то в минимальном пути от вершины A к вершине B нет промежуточных вершин. Таким образом, этот путь будет A → B.

Элемент δ21,2 матрицы 2, соответствующий второму по протяженности пути от вершины A к вершине B:

δ1,22 = min[...]=35.

2

Так как второе по минимуму выражение находится на четвертом месте, что соответствует вершине D, то второй по протяженности путь от вершины A к вершине B проходит через вершину D.

Рассмотрим для примера нахождение кратчайшего пути от вершины A к вершине C. Тогда

δ11,3 = min[(γ1,1 +d1,3 );(γ1,2 +d2,3 );(γ1,3 +d3,3 ); 1

(γ1,4 +d4,3 );(γ1,5 +d5,3 );(γ1,6 +d6,3 )] =

= min[(∞+ 40);(30 +15);(∞+0);(20 + 22);(∞+ 25);(∞+ 45) = 40.

Так как минимум находится на 4-м месте, кратчайший путь от A к C проходит через вершину D. Чтобы найти кратчайший путь от вершины D к вершине C необходимо вычислить

δ14,3 = min[(γ4,1 +d1,3 );(γ4,2 +d2,3 );(γ4,3 +d3,3 ); 1

(γ4,4 +d4,3 );(γ4,5 +d5,3 );(γ4,6 +d6,3 )] =

= min[(20 + 40);(15 +15);(20 +0);(∞+ 20);(∞+ 25);(40 + 45) = 20.

Так как минимум находится на 3-м месте, то между вершинами D и C нет промежуточных вершин. Таким образом кратчайший путь от вершины A к вершине C будет A → D → C.

103

Поступая аналогичным образом, можно составить матрицу кратчайших путей между всеми вершинами, где в качестве элементов находятся не расстояния, а идентификаторы промежуточных или конечных вершин. Для рассматриваемого примера такая матрица будет иметь следующий вид:

A

B

C

D

E

F

A

–

B

D

D

D

D

B

D

–

C

D

C

D

C

D

B

–

D

E

E

.

D

A

B

C

–

C

F

E

D

D

C

D

–

F

F

A

D

D

D

E

–

Выбрав кратчайшие пути от какого-либо узла ко всем остальным, можно построить так называемое дерево кратчайших путей, в котором из всего множества путей от узла указаны только кратчайшие от него пути ко всем остальным узлам.

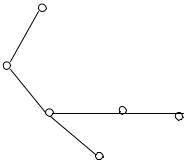
Например, для графа (см. рис. 5.2), которому сопоставлена матрица L1 непосредственных связей, дерево кратчайших путей изобра-

B			жено на рис. 5.4.
			Дерево кратчайших путей являет-
A			ся поддеревом дерева путей (рис. 5.5).
			Дерево кратчайших путей и де-
	C		рево путей от узла ко всем осталь-
D		E	ным узлам для неориентированных
			графов (сетей) совпадает с деревом
			кратчайших путей и деревом путей
	F		соответственно от всех узлов к рас-
Рис. 5.4. Дерево кратчайших путей			сматриваемому узлу i. Для ориен-
от вершины А ко всем остальным			тированных графов (сетей связи)
вершинам			такого совпадения может и не
			быть.

104

F

D E

C D F

E

D

B F

C E

F D F E

A C

F

B C E

D

C E

F

F E C

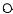B

B

D

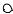C

Рис. 5.5. Дерево путей от вершины А к остальным вершинам

5.2.Выбор оптимальных маршрутов

спомощью метода рельефов

Этот метод относится к групповым распределенным методам динамического управления [6]. Критерием выбора пути является минимизация длины пути, выраженная числом транзитных участков. На сети связи при применении этого метода должны выполняться операции формирования рельефа и его коррекция.

Формирование рельефа осуществляется в начальный момент времени (в момент пуска сети) и при развитии сети, т. е. при вводе в действие новых узлов коммутации.

105

Коррекция выполняется периодически в процессе функционирования сети или в момент возникновения повреждений или перегрузок.

Рассмотрим эти операции.

В момент пуска сети формирование рельефа начинается с некоторого узла УКα, α = 1,2, …, N, где N – число УК на сети.

Начинается построение α-рельефа. В запоминающих устройствах каждого УКi сети отводится объем памяти

N × Mi,

где Mi – число исходящих направлений из УКi. Туда заносится матрица рельефов Ri.

При формировании рельефа из УК-инициализатора во всех исходящих из него направлений передается цифра 1. Эта единица на соседних с УК-инициализатором узлах заносится в матрицу Ri по координатам

(n, m1),

где n – номер УК-инициализатора; m1 – номер ветви, по которой поступила единица.

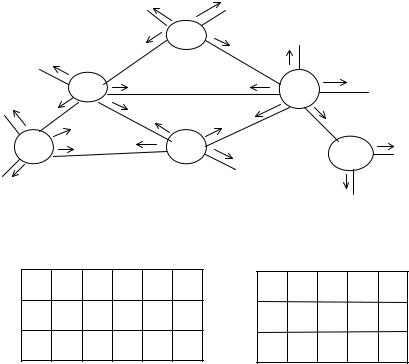
Пусть имеется сеть, изображенная на рис. 5.6. Далее процесс построения рельефа будет следующим.

Все УК, в которые поступила цифра 1, передают по всем исходящим направлениям, за исключением того направления по которому поступила 1, цифру 2. Эта цифра во всех УК, в которые она поступила, заносится в матрицу Ri по координатам

(n, m2),

где m2 – номер ветви, по которой поступила цифра 2.

В примере цифра 2 будет занесена в матрицу RB, RC, RD, RE, RF. Теперь УК, на которые поступила цифра 2, передают по исходящим

направлениям цифру 3 и т. д.

При этом должны соблюдаться следующие правила.

1. Если в УК поступили одинаковые цифры с двух и более направлений, данный УК инициирует передачу цифры на единицу больше поступившей по всем без исключения исходящим направлениям. Например, в УКЕ цифра 2 поступает с направлений, идущих от УКВ и УКС. В этом случае цифра 3 с УКЕ передается по всем исходящим направлениям.

106

а)			1	1
			1	УКA
2
	УКB	2
2		2
3
	4		3
УКD	3	3		УКE
3
б)
RB – УКА βBA	βBC	βBD	βBE
1	2	4	3

RD – УКА βDB βDE

RE – УКА βEB

1

2

2

2 УКC

2

3

2

3

3УКF

3

RC – УКА βBC βCB βCE

1 2 3

βTC βED

RE – УКА βFC

	2	3				2	2	3
												2

Рис. 5.6. Вычислительная сеть и матрицы рельефов

2. Если в УК поступает цифра с одного направления, на данном УК происходит инициализация для передачи цифры на единицу больше той, которая поступила по всем направлениям, за исключением того направления, по которому передана данная цифра.

Передача цифры по этому направлению возможна лишь при поступлении в данный УК следующей цифры.

107

Цифра, передаваемая по этому направлению, должна быть на единицу больше цифры , поступающей второй по порядку. Например, в УКD цифра 2 поступает по одному направлению – от УКВ. Тогда цифра 3 с УКD должна передаваться по всем направлениям, за исключением направления к УКВ. По этому направлению будет передана цифра 4, так как следующая по порядку цифра, поступившая в УКD, это цифра 3.

3. Инициализация передачи цифр по всем направлениям на каждом УК происходит один раз после поступления первой цифры по порядку. Например, при передаче цифры 3 на УКС от УКЕ она заносится в матрицу RC по соответствующим координатам, а инициализация передачи следующей по порядку цифры уже не происходит, так как ранее была осуществлена передача цифры 2.

Так будет сформирован α-рельеф. Аналогично строятся рельефы для всех остальных узлов сети.

Считается, что рельеф сформирован, если построены все α-релье- фы (α = 1, 2, … N).

Поиск оптимального пути при установлении соединения от УКi к УКj состоит в отыскании в УКi и в каждом промежуточном УК ветви, которой соответствует минимальное число в строке матрицы рельефов для УКj.

Рассмотрим два примера.

1.Пусть требуется установить соединение от УКD к УКА ( рис. 5.6, а). На УКD происходит обращение к строке матрицы рельефов RD, cоответствующей УКА (рис. 5.6, б). Соединение установлено по ветви, которой соответствует минимальное число в этой строке. Для рассматриваемого примера это ветвь βDB.

На УКВ процесс поиска оптимального пути повторяется. В данном случае будет выбрана ветвь βВА.

Если в этой ветви нет свободных каналов, то выбирается ветвь, которой соответствует следующее по порядку число, т. е. ветвь βВС и т. д.

При выборе пути возможно возникновение "петель", т. е. когда соединение дважды проходит через один и тот же узел.

2.Пусть требуется установить соединение от УКD к УКA. На УКD выбирается ветвь βDB. Пусть теперь в ветви βBA нет ни одного свобод-

ного канала. Тогда вызов согласно матрице RB перенаправляется по ветви βBC. Если в ветви βCA тоже нет свободных каналов, то согласно матри-

108

це RC вызов должен быть направлен обратно на УКВ. Это первый тип "петли". При соответствующей итерации данный вызов может блуждать по сети по такой петле: βDB, βBC, βCE, βCB. Вызов дважды попадает в УКВ. Это второй тип "петли".

Появление петель первого и второго типов недопустимо. Способ борьбы с возникновением петель заключается в том, что в процессе распространения по сети вызов "запоминает" номера УК, через которые он прошел, чтобы не проходить через них дважды.

Ситуация на сети непрерывно меняется:

одни направления перегружаются, а нагрузка других уменьшается; могут выйти из строя каналы связи; могут быть повреждения в отдельных направлениях связи и УК.

Поэтому необходима коррекция рельефа сети. Рассмотрим процесс обмена служебной информацией между управляющими устройствами (УУ) соседних узлов УКi, УКl, УКm (см. рис. 5.6, а) при коррекции рельефа сети.

Пусть в УКi хранится матрица рельефов Ri (рис. 5.7, б). Пусть поступил сигнал начала передачи служебной информации о рельефах на соседние УК. Тогда УУ считает из ЗУ, в котором хранится матрица Ri, элемент первой строки и найдет минимальный из них.

Предположим, что минимальным элементом, т. е. элементом с минимальной высотой 1-го рельефа, будет r1,l. Это означает, что кратчайший путь из УКi до УК1 проходит через узел УКl , а число транзитных участков в нем равно r1,l . Согласно определению формирования рельефа УУ, прибавив единицу к этому элементу, получим элемент

ri = min (r		,..., r , r	,..., r	)+1,
1	1,i1	1,1 1,m	1,in
	i

который необходимо передать на соседние узлы. Значение r1i равно высоте l рельефа тех ветвей, которые связывают узлы с УКi.

Однако в рассматриваемой распределенной системе динамического управления элемент r1i не передается на соседние узлы до тех пор, пока не будут определены другие элементы, соответствующие другим рельефам, т. е.

ri	= min (r	,..., r , r	,..., r	)+1;
2	2,i1	2,1 2,m	2,in
	i

109

а)	R1	R1

УК1

R1

			Ri
		Ri
		У						Rm
		УКi		Ri
		i			Rm
							У
							УКmm		Rm
					...			β1i	...
б)					УК1
					Ri–УКj
					УКN
		βii1 ...	βil	βim ...	βiin			Ri
	УК	r	r1i	r1m	r1 ln
	1	11
	R –УК	rj1	rj1	rjm	rj in
	i	j
	УКN	rN1	rN1	rNm	rN in			Ri
					...			βmi	...

УК1

Rm–УКj

УКN

Рис. 5.7. Пример обмена служебной информацией между узлами коммутации и матрицы рельефов

110