13. Найдите U, если R1 R2

5 Ом, I2 2

А, а I3 (U3 ) 0,01 U32 .

I1

а. 25 В.

R1

U3

U

б. 10 В.

R2

в. 15 В.

I2

I3

г. 5 В.

ГЛАВА 3. НЕЛИНЕЙНЫЕ ЦЕПИ ПЕРЕМЕННОГО ТОКА

3.1. Цепи с резистивными нелинейными элементами

Искажение формы кривой тока нелинейными резисторами. В цепях переменного тока, содержащих нелинейные резисторы, наблюдается весьма своеобразное явление искажения формы кривой тока цени, если она питается синусоидальным напряжением.

Рассмотрим это явление в простейшем случае, когда цепь состоит из одного безынерционного нелинейного резистора (рис. 3.1).

Рис. 3.1. Электрическая цепь с нелинейным резистором

Совместим его вольт-амперную характеристику u f i , построенную по мгновенным значениям напряжения u и тока i , с временной диаграммой u f t приложенного к резистору синусоидального напряжения, как это показано на рис. 3.2. Выбрав на оси абсцисс диаграммы (рис. 3.2, б) несколько произвольных моментов времени t1, t2 ,... (в пределах первой четверти периода),

включая момент tm , когда напряжение достигает максимального значения U m , определим соответствующие мгновенные значения u1, u2 ,... напряжений и снесем их на вольт-амперную характеристику (рис. 3.2, а). Найдя по этим напряжениям токи i1,i2 ,... резистора, соответствующие тем же моментам времени, отложим их в определенном масштабе на правой диаграмме (на рис. 3.2 операциями a, b, c показано построение тока i2 , соответствующего моменту t2 ). Соединив полученные точки плавной кривой, мы получим временную диаграмму тока i f t , которая показывает, что ток резистора оказывается несинусоидальной функцией времени.

Рис. 3.2. Характеристика тока i f t при наличии в цепи резистора с симметричной вольт-амперной характеристикой

Проделав аналогичные построения в пределах второй четверти периода, нетрудно продолжить кривую тока i f t , которая, очевидно, будет симмет-

рична относительно вертикальной оси, проведенной через максимум кривой напряжения (штриховая линия на рис. 3.2, б).

Если нелинейный резистор обладает симметричной вольт-амперной характеристикой, то и ток в нем при синусоидальном напряжении будет симметричным, то есть во второй полупериод кривая тока, располагаясь под осью абсцисс, повторит кривую первого полупериода. Подчеркиваем, что в гармоническом составе такого тока будут присутствовать только нечетные гармоники. При несимметричной вольт-амперной характеристике резистора, например, такой, как показано на рис. 3.3, а, несимметричной будет и кривая тока (рис. 3.3, б), то есть в его разложении появятся четные гармоники и, как правило, постоянная составляющая.

Искажение формы кривой напряжения нелинейными резисторами.

Если по линейному резистору пропускать синусоидальный ток, то напряжение на резисторе будет несинусоидальным. В этом легко убедиться, проделав соответствующие построения, аналогичные показанным на рис. 3.2. Для удобства этих построений, представленных на рис. 3.4, вольт-амперную характеристику нелинейного резистора целесообразно повернуть на 90° так, чтобы ось тока совпала по направлению с осью ординат временной диаграммы (для уяснения построений на рис. 3.4 рекомендуем проследить их для момента t1 в последова-

тельности операций a, b, c ).

Рис. 3.3. Характеристика тока i f t при наличии в цепи резистора с несимметричной вольт-амперной характеристикой

Рис. 3.4. Характеристика напряжения u f t при наличии в цепи резистора с симметричной вольт-амперной характеристикой

В случае симметричного резистора кривая напряжения получается симметричной относительно оси времени, то есть она может быть представлена рядом нечетных гармоник без постоянной составляющей.

Коэффициент мощности цепей с нелинейными резисторами. До сих пор мы убеждались, что в резистивных цепях коэффициент мощности равен единице. Это утверждение, однако, справедливо только для линейных цепей. В нелинейных же цепях, даже при отсутствии в них катушек и конденсаторов, коэффициент мощности оказывается ниже единицы.

Покажем это, проанализировав выражение для коэффициента мощности

UPI

врассмотренном выше случае цепи с нелинейным резистором (см. рис. 3.1) при питании ее от источника с синусоидальным напряжением. Поскольку здесь наблюдаются искажение формы кривой тока и появление в нем высших гармоник, мощность цепи следует рассматривать как сумму мощностей отдельных гармоник. Останавливаясь на простейшем случае симметричной формы кривой тока, когда в нем присутствуют только нечетные гармоники, для мощности цепи имеем

P P1 P3 P5 ... U1I1 U3 I3 U5 I5 ....

Вследствие того, что питающее напряжение синусоидально и, следовательно, не содержит высших гармоник, в выражении для мощности цепи остается только первый член

P P1 U1I1 UI1 ,

где U - действующее значение напряжения, совпадающее с понятием действующего значения U1 его первой гармоники.

Поэтому для коэффициента мощности окончательно получим

UPI II1 I ,

то есть коэффициент мощности такой цепи равен коэффициенту синусоидальности тока, который при искажении формы кривой тока меньше единицы.

3.2. Цепи с индуктивными нелинейными элементами

Ферромагнитная катушка как нелинейный элемент цепи переменного тока. Индуктивная катушка с ферромагнитным магнитопроводом (рис. 3.5), кратко называемая здесь ферромагнитной катушкой, является наиболee распро-

страненным на практике нелинейным элементом цепи переменного тока. Ее нелинейность является следствием нелинейности характеристики намагничивания B f H ферромагнитных материалов, то есть зависимости между магнитной

индукцией В и напряженностью поля H в этих материалах, и выражается в нелинейности магнитной характеристика катушки, представляющей собой зависимость потокосцепления обмотки от тока i в ней. При условном графическом изображении ферромагнитных катушек на принципиальных электрических схемах, когда требуется подчеркнуть их нелинейность, прибегают к общему символу нелинейности (рис. 3.6, а), перечеркивая условное изображение катушки косой ломаной линией. Однако чащеприменяют специальное условное обозначение магнитопровода в виде жирной черты, проведенной рядом с изображением катушки (рис. 3.6, б).

Рис. 3.5. Катушка с ферромагнитным магнитопроводом

Рис. 3.6. Обозначения нелинейной индуктивности в цепях

Основные явления в ферромагнитных катушках. Магнитное поле фер-

ромагнитной катушки целесообразно разделять на две части - основное поле, целиком локализованное в магнитопроводе, и поле рассеяния, линии которого полностью или преимущественно замыкаются в окружающем пространстве. Соответственно на две составляющие разделяют и потокосцепление обмотки:

Ψ Ψ0 ΨS ,

первую из которых ( Ψ0 ) называют основным потокосцеплением, а вторую (ΨS )

— потокосцеплением рассеяния. При этом нелинейно с током связано только основное потокосцепление, определяющееся основным магнитным потоком Φ0 (потоком магнитопровода) и числом витков w обмотки простой формулой

Ψ0 wΦ0 ,

так как основное поле сцепляется со всеми витками обмотки. Потокосцепление рассеяния зависит от тока линейно, поскольку окружающее магнитопровод пространство, как правило, характеризуется постоянной магнитной проницаемостью, кстати, практически равной магнитной постоянной 0 .

Рис. 3.7. Магнитная характеристика Φ0 f i катушки

Анализ работы ферромагнитных катушек при переменном токе осложнен и рядом других явлений. В первую очередь здесь следует обратить внимание на вихревые токи, которые индуктируются в магнитопроводе переменным магнитным полем катушки. Они, как и всякие индуктированные токи, ослабляют магнитное поле катушки и вызывают нагревание магнитопровода. Последнее усугубляется также потерями энергии в магнитопроводе, вызванными явлением гистерезиса в материале магнитопровода. Немаловажную роль играет и активное сопротивление r0 обмотки, определяющее, в частности, процесс ее нагре-

вания протекающим током.

Одновременный учет всех упомянутых выше явлений весьма затруднителен, поэтому, приступая к анализу работы ферромагнитных катушек при переменном токе, мы сначала остановимся на идеальной ферромагнитной катушке, в которой предположим отсутствие всех перечисленных явлений за исключением нелинейной связи Φ0 f i между основным магнитным потоком Φ0 и то-

ком i в обмотке (рис. 3.7). Очевидно, что эта связь имеет тот же характер, что и

магнитная характеристика катушки f i . Таким образом, идеальная ферро-

магнитная катушка, оставаясь нелинейным элементом, лишена потоков рассеяния, активное сопротивление ее обмотки равно нулю, в материале магнитопровода не наблюдаются гистерезиса, а вихревые токи в теле магнитопровода отсутствуют.

Влияние насыщения на форму кривой тока катушки. Как и в случае нелинейных резисторов, в ферромагнитных катушках наблюдаются искажения форм кривых тока или напряжения. В частности, если к ферромагнитнои катушке приложить синусоидальное напряжение, то ток в ней оказывается несинусоидальным.

Покажем это на примере идеальной катушки, для которой на основании второго закона Кирхгофа, записанного для контура обмотки (рис. 3.8), имеем

u e0 ,

то есть приложенное к катушке мгновенное напряжение u по абсолютной величине равно индуктирующейся в ней мгновенной ЭДС e0 . Следовательно,

формы кривых напряжения и ЭДС в идеальной катушке будут одинаковыми. Например, при синусоидальном напряжении на катушке ЭДС в ней будет также синусоидальной.

Рис. 3.8. Схема идеальной катушки Обращаясь далее к закону электромагнитной индукции, выражающему

ЭДС через магнитный поток Φ0 катушки и число витков w ее обмотки e0 w ddΦt0 ,

нетрудно прийти к выводу, что в рассматриваемых условиях магнитный поток будет также синусоидальным (точнее, косинусоидальным), так как только косинусоидальная функция после дифференцирования дает синусоидальную функцию.

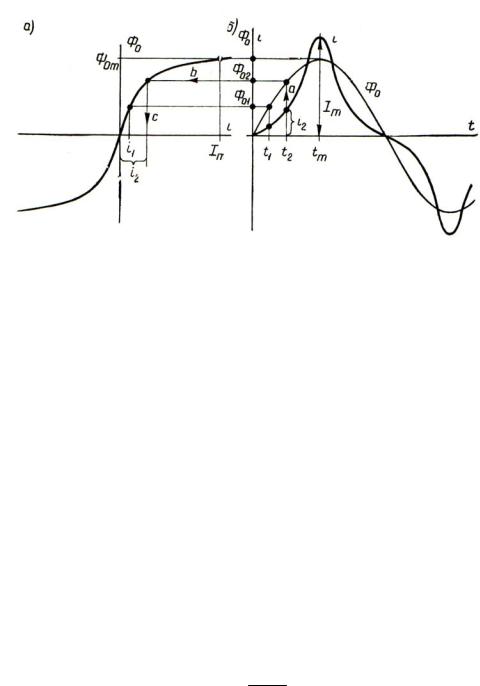
Нанеся синусоиду потока Φ0 на временную диаграмму (рис. 3.9, б), расположим рядом с ней, как указано на рис. 3.8, а, магнитную характеристику катушки Φ0 f i и описанным выше приемом (см. рис. 3.2) выполним необходимые построения для определения кривой тока i катушки (построение тока, соответствующего моменту t2 на рис. 3.9, отражено операциями a, b, c ).

Рис. 3.9. Магнитная характеристика Φ0 f i катушки

Обращаем внимание на типичность пикообразной формы полученной кривой тока ферромагнитной катушки при ее питании синусоидальным напряжением. При этом, чем дальше заходит максимальное значение Φ0m магнитно-

го потока за колено кривой магнитной характеристики катушки, тем острее становится пик в кривой тока.

Искажение формы кривой напряжения катушки. Остановимся теперь на случае, когда по обмотке идеальной ферромагнитной катушки (см. рис. 3.8) протекает синусоидальный ток i . Располагая рядом с временной диаграммой тока (рис. 3.10, б) магнитную характеристику катушки Φ0 f i так, как это

показано на рис. 3.10, а, мы, пользуясь приемом, аналогичным показанному на рис. 3.4, можем построить кривую основного магнитного потока Φ0 (операции

a, b, c на рис. 3.10), которая вследствие явления насыщения будет иметь упло-

щенную форму (рис. 3.10, б). Ориентируясь на закон электромагнитной индукции

e0 w ddΦt0 ,

определяющий ЭДС через производную от магнитного потока по времени, нетрудно представить себе кривую этой ЭДС, показанную на рис. 3.10, б штриховой линией.

Подчеркнем, что в связи с наличием знака минус в законе электромагнитной индукции ЭДС в интервале, где поток падает (производная отрицательна), будет положительна, а где поток возрастает - отрицательна. При этом максимум ЭДС совпадет с моментом, когда кривая Φ0 проходит через нуль (наиболее

крутой участок кривой Φ0 ), а в точках, где поток имеет максимум, кривая е0 пересечет ось абсцисс. Характерно, что крутой участок кривой магнитного потока Φ0 , в пределах которого ЭДС достигает высоких значений, занимает от-

носительно небольшую часть периода. Поэтому кривая ЭДС будет отличаться пикообразной формой.

Рис. 3.10. Кривая напряжения катушки с магнитопроводом Кривая напряжения u на катушке будет представлять собой ту же кри-

вую, что и ЭДС, но опрокинутую относительно оси абсцисс, поскольку напряжение и ЭДС равны друг другу по абсолютной величине и противоположны по знаку (u e0 ). Таким образом, напряжение на ферромагнитной катушке при

синусоидальном токе в обмотке несинусоидально и характерно своей пикообразной формой.

Средняя ЭДС катушки. Выведем важное в электроизмерительной технике выражение для средней ЭДС, индуктирующейся в замкнутом контуре периодически меняющимся потокосцеплением. Не связывая себя какими-либо дополнительными частными условиями, предположим, что потокосцепление контура в течение полупериода монотонно изменяется в пределах от Ψmax до

Ψmin (рис. 3.11). Для мгновенной ЭДС, индуктируемой этим потокосцеплением, рассматриваемый отрезок времени будет соответствовать ее положительной

полуволне, так как в начале интервала (при Ψ Ψmax ) и в его конце (при Ψ Ψmin ) ЭДС равна нулю; в остальные же моменты времени в пределах этого

интервала ЭДС принимает положительные значения, поскольку потокосцепление непрерывно падает. Поэтому для средней ЭДС за этот полупериод имеем

		2	0,5T	2	0,5T d		2	min
	ECP		e d t			d t			d .
		T		T 0 d t			T
			0
								max

Рис. 3.11. Изменение потокосцепления контура в течение полупериода

Последнее преобразование, которое формально можно рассматривать как сокращение подынтегрального выражения на d t , по существу, является пере-

ходом к новой независимой переменной , что требует соответствующей замены пределов интегрирования. Поскольку в начальный момент времени t 0 потокосцепление было равно Ψmax , то это его значение и следует рассматривать в качестве нижнего предела. Верхним пределом будет являться потокосцепление Ψmin , соответствующее моменту времени t 0,5T .

Выполняя интегрирование, получим

ECP T2 Ψmin Ψmax 2 f Ψmax Ψmin ,

так как период T и частота f являются взаимообратными величинами. Вводя понятие о размахе колебаний потокосцепления

Ψ Ψmax Ψmin ,

предыдущее выражение можно записать более кратко:
ECP 2 f ΔΨ.	(3.1)
В частном случае, когда нотокосцепление меняется по симметричному
закону между значениями Ψmax Ψm и Ψmin Ψm (рис. 3.12),	для средней
ЭДС получим
ECP 4 f Ψ.	(3.2)

Применительно к ферромагнитным катушкам, в частности для ЭДС, индуктируемой основным магнитным потоком, это общее выражение часто записывают в развернутой форме:

E0CP 4Ф0m w f или E0CP 4Bm sw f ,

выражая эту ЭДС через максимальные значения Ф0m потока или Bm индукции в

магнитопроводе, площадь s его поперечного сечения и число витков w обмотки.

Действующая ЭДС катушки. Используя выводы предыдущего пункта; действующую ЭДС, индуктирующуюся в замкнутом контуре, можно определить по средней ЭДС и коэффициенту формы kФе ее кривой:

E kФеECP ,

то есть в виде (при симметрично изменяющемся потокосцеплении)

E 4kФе f Ψm .

(3.3)

Рис. 3.12. Изменение потокосцепления контура по симметричному закону

Тогда, обращаясь к частному случаю ферромагнитной катушки, для ЭДС, индуктирующейся в ее обмотке основным магнитным потоком, можно написать:

E 4kФе f wФ0m	(3.4)
или
E 4kФе f wsBm ,	(3.5)

если вместо потокосцепления m обратиться к максимальным значениям потока Ф0m или магнитной индукции Bm .

Следует подчеркнуть, что практически точное значение действующей ЭДС по этим формулам удается получить только в частном случае синусоидальной ЭДС, когда коэффициент формы равен kФе 1,11. Предыдущие форму-

лы принимают в этом случае вид

E 4,44 f wФ0m или E 4,44 f wsBm .

Во всех остальных режимах коэффициент формы kФе кривой ЭДС, как

правило, остается неизвестным и использование приведенных формул, строго говоря, становится невозможным. Однако на практике в подобных случаях часто довольствуются приближенным вычислением ЭДС по последним формулам, условно принимая коэффициент формы равным 1,11.

Влияние гистерезиса на форму кривой тока. Выясним теперь, как по-

влияет явление гистерезиса в материале магнитопровода на форму кривой тока ферромагнитной катушки при питании ее от источника с синусоидальным напряжением. Последнее условие, как было показано ранее, определяет синусоидальный закон изменения магнитного потока Φ0 в магнитопроводе (рис. 3.13,

б), который при наличии гистерезиса будет перемагничиваться между крайними магнитными состояниями соответствующими потокам Φ0m и Φ0m по

петле гистерезиса (рис. 3.13, а).

Пользуясь приемом, использованным в рис. 3.2, построим на рис. 3.13 кривую тока i катушки. Учтем только, что при возрастании магнитного потока перемагничивание идет по восходящей ветви петли (правая на рис. 3.13, а), а при убывании потока — по нисходящей ветви (левая на рис. 3.13, а). Так например, к моменту времени t 0 , когда магнитный' поток, возрастая, проходит значение Φ0 0 , ток в катушке должен иметь значение i0 , показанное на рис.

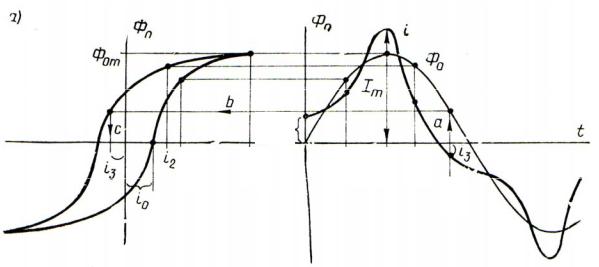
3.13 фигурной скобкой. После момента tm обратим внимание на построение тока i3 в момент t3 (операции a, b, c ), когда, несмотря на положительное значение потока Φ0 , ток приобретает отрицательную величину. В течение второй

половины периода форма кривой тока повторяется, и ее можно вычертить как зеркальное изображение кривой за первую половину периода в оси абсцисс.

Сопоставляя форму кривой тока в катушке при отсутствии (рис. 3.9, б) и наличии гистерезиса (рис. 3.13, б), нетрудно уловить изменения, вносимые в форму тока явлением гистерезиса. Во-первых, под влиянием гистерезиса кривая тока теряет симметрию относительно вертикальной оси, проведенной через максимум тока. Во-вторых, при наличии гистерезиса можно говорить об опережении тока по отношению к магнитному потоку. Действительно, хотя максимумы тока и потока совпадают по времени (рис. 3.13, б), но момент перехода кривой тока через ноль наступает раньше нуля магнитного потока. Таким образом, в среднем магнитный поток можно считать отстающим от тока.

а)				б)

	i		i0
i1	Im		t1 tm t2

t3

Рис. 3.13. Форма кривой тока ферромагнитной катушки i f t при учёте гистерезиса

Следует, однако, заметить, что последние рассуждения имеют сугубо качественный характер, так как строгого понятия о разности фаз двух различающихся по форме кривых не существует, и определить угол сдвига между током и потоком по рис. 3.13, б не представляется возможным.

Векторная диаграмма идеальной катушки. Очевидно, что прибегать к векторным диаграммам при анализе работы ферромагнитных катушек как элементов, в которых по крайней мере одна из величин (ток или напряжение) ока-

зывается несинусоидальной, можно только при условии их замены эквивалентными синусоидами (гл. 1, п. 1.5). Напомним также, что магнитные потоки и потокосцепления изображают векторами не действующих, а максимальных значений этих величин.

Построим диаграмму идеальной катушки с учетом явления гистерезиса в ее магнитопроводе. В этом случае, как мы убедились в предыдущем пункте, ее основной магнитный поток Φ0 отстает по фазе от тока i . Поэтому расположив,

как это обычно принято, вектор 0m магнитного потока горизонтально (рис.

3.14), вектор I тока в катушке направим по отношению к потоку в сторону опережения на некоторый угол , называемый углом магнитного запаздывания

(магнитный поток запаздывает по отношению к току). Вектор ЭДС E 0 , индуктируемой в обмотке основным магнитным потоком, как известно, отстает от вектора потока точно на 90° и поэтому на диаграмме будет направлен вниз. Так как напряжение на идеальной катушке и ее ЭДС равны по величине и обратны по знаку, то есть

u e0 или U E0 ,

то вектор напряжения U будет представлять собой перевернутый вектор ЭДС

E0 (рис. 3.14).

Рис. 3.14. Векторная диаграмма катушки с ферромагнитным магнитопроводом

На полученной диаграмме часто прибегают к разложению вектора тока на две взаимно-перпендикулярные составляющие, одну из которых I направляют

вдоль вектора магнитного потока, а вторую I — перпендикулярно к вектору

потока. В связи с тем, что первая составляющая направлена перпендикулярно к вектору напряжения, ее можно называть реактивным током катушки. Соответственно вторую составляющую, совпадающую с напряжением, естественно называть активным током. Тем не менее при обозначении этих составляющих избегают применять привычные индексы «р» и «а», изменяя их на « » и « ».

Оценка угла магнитного запаздывания. На векторной диаграмме катуш-

ки (рис. 3.14) обращает на себя внимание угол между векторами эквивалентных синусоид тока и напряжения, который, как следует из построений, оказывается меньше 90°. Это свидетельствует о том, что в катушке наблюдается расход мощности:

PГ U I cos .

Поскольку мы рассматриваем идеальную катушку с сопротивлением обмотки, равным нулю, активная мощность катушки может явиться следствием только явления гистерезиса в магнитопроводе, то есть представлять собой мощность потерь гистерезиса, что и подчеркнуто в ее обозначении индексом «Г» Тогда, принимая во внимание, что углы и являются взаимно дополняющими друг друга до 90° (см. рис. 3.14), для угла имеем

sin cos UPГI .

Этой формулой и определяется угол магнитного запаздывания через мощность потерь на гистерезис в магнитопроводе катушки.

Влияние вихревых токов на режим работы катушки. Вихревые токи,

индуктирующиеся в магнитопроводе катушки, сказываются на ее работе в двух направлениях.

Во-первых, замыкаясь в теле магнитопровода, вихревые токи вызывают его нагревание и, следовательно, дополнительный расход энергии в катушке, который оценивают мощностью PB потерь на вихревые токи. Отсюда вытекает,

что вихревые токи приводят к увеличению угла магнитного запаздывания, величина которого при совместном проявлении гистерезиса и вихревых токов определяется выражением

sin	PM	,	(3.6)
	U I

числитель которого представляет собой сумму

PM PГ РВ

мощностей РГ и РВ потерь на гистерезис и вихревые токи и называется мощ-

ностью полных магнитных потерь катушки.

Во-вторых, вихревые токи, циркулируя внутри магнитопровода, создают свое собственное магнитное поле, которое согласно принципу Ленца, будет ослаблять основное поле катушки, так как именно оно является причиной возникновения вихревых токов. Поэтому говорят, что вихревые токи оказывают на катушку размагничивающее действие.

Размагничивающее действие вихревых токов можно более строго рас-

смотреть по развернутой векторной диаграмме идеальной катушки, в которой с целью упрощения пренебрежем явлением гистерезиса. Кроме того, в отличие от предыдущих построений (рис. 3.14) в новой диаграмме удобнее оперировать не током I катушки, а пропорциональной ему величиной wI — магнитодвижущей силой (МДС) обмотки, вектор которой будет совпадать по направлению с вектором тока I .

Построение диаграммы начнем с вектора 0m основного магнитного по-

тока катушки (рис. 3.15) и вектора F результирующей МДС катушки, определяющейся на этот раз совместным действием тока в обмотке и вихревых токов в магнитопроводе. Поскольку мы пренебрегаем явлением гистерезиса, то результирующая МДС должна совпадать по фазе с потоком и, следовательно,

вектор F будет направлен вдоль вектора 0m . Построим теперь вектор EB ,

изображающий собой совокупность вихревых ЭДС, то есть ЭДС, под действием которых возникают в магнитопроводе вихревые токи. Эти ЭДС индуктированы основным магнитным потоком и поэтому должны отставать от него по фазе точно на 90°. Совокупность вихревых токов, которая также может быть представлена одним вектором I B , в свою очередь, будет отставать от ЭДС на некоторый угол B (рис. 3.15). Отставание вихревых токов от вихревых ЭДС

объясняется тем, что эти токи, замыкаясь по контурам магнитопровода, создают магнитное поле самоиндукции, то есть ведут себя как обычные переменные токи, протекающие по обычным индуктивным контурам. Естественно, что контуры вихревых токов обладают и определенным активным сопротивлением, по-

токов.

этому угол B должен быть меньше 90° (на диаграмме для определенности он

принят равным 45°).

Поскольку вихревые токи замыкаются в теле магнитопровода по одновитковым контурам, вектор IB можно рассматривать как вектор МДС вихревых

Вектор wI МДС обмотки теперь нетрудно построить, исходя из условия, что результирующая МДС катушки равна геометрической сумме МДС обмотки и вихревых токов:

F wI IB .

Рис. 3.15. Векторная диаграмма катушки с ферромагнитным магнитопроводом

F wI IB .

Иначе говоря, МДС wI обмотки должна представлять собой такой вектор, который в сумме с вектором I B должен дать вектор F результирующей

МДС (рис. 3.15). Анализируя полученную диаграмму, нетрудно прийти к уже сформулированному в предыдущем пункте выводу о том, что вихревые токи приводят, во-первых, к отставанию магнитного потока по фазе от МДС обмотки или, что то же самое, от тока катушки и, во-вторых, к уменьшению результирующей МДС катушки по сравнению с МДС обмотки. Последнее и означает, что вихревые токи оказывают размагничивающий эффект в ферромагнитной катушке.

Влияние гистерезиса и вихревых токов на электрические параметры катушки. Гистерезис и вихревые токи влияют не только на магнитный режим катушки, но сказываются и на ее электрических параметрах, в частности на активном и реактивном сопротивлениях катушки.

Прежде всего следует обратить внимание на то, что учет явлений гистерезиса и вихревых токов приводит даже в идеальной ферромагнитной катушке, то есть при отсутствии активного сопротивления обмотки, к конечному значению активного сопротивления катушки в целом. Действительно, активное сопротивление элемента цепи переменного тока определяется отношением

r IP2

активной мощности данного элемента к квадрату действующего тока в нем. Поскольку гистерезис и вихревые токи вызывают нагрев магнитопровода, то есть влекут за собой расход мощности в катушке, то ее активное сопротивление уже не будет равняться нулю, а приобретет определенное значение:

r PIM2 ,

где PM – мощность потерь в магнитопроводе; I —ток в обмотке катушки.

При этом, чем ярче проявляются гистерезис и вихревые токи, то есть чем выше мощность потерь, тем больше активное сопротивление катушки.

Вихревые токи, кроме того, оказывают влияние и на реактивное сопротивление катушки. Например, при работе катушки в условиях неизменного тока, то есть неизменной МДС обмотки, вихревые токи приводят к уменьшению результирующей МДС катушки и, следовательно, к уменьшению ее магнитного потока. Это влечет за собой снижение ЭДС в обмотке

E0 4kФе f wΦ0m

или, что то же уменьшение напряжения U на ней, так как последнее в идеальной катушке равно ЭДС.

Если катушка работает при неизменном напряжении U, то есть при неизменной ЭДС E0 , то, как следует из приведенной выше формулы, магнитный

поток Φ0m также должен оставаться постоянным. Это значит, что, несмотря на

размагничивающее действие вихревых токов, должна сохраняться результирующая МДС катушки, что возможно только в том случае, если увеличится ток обмотки. Поэтому в рассмотренном весьма часто встречающемся на практике режиме вихревые токи в магнитопроводе приводят к увеличению тока обмотки.

Очевидно, что в обоих рассмотренных случаях речь идет об уменьшении полного сопротивления катушки

z UI ,

равного отношению напряжения U на катушке к ее току I . Естественно, что это уменьшение z определяется исключительно уменьшением реактивного сопротивления катушки, ибо ее активное сопротивление, как мы убедились ранее, возрастает под влиянием гистерезиса и вихревых токов.

Вольт-амперная характеристика катушки. Исключительно важную роль в оценке поведения ферромагнитной катушки в цепях переменного тока играет ее вольт-амперная характеристика, представляющая собой зависимость U F I между действующими напряжением U и током I катушки. Характер этой зависимости можно уловить, используя формулу

E0 4kФе f wsBm ,

принимая во внимание, что напряжение на идеальной катушке равно ее ЭДС, то есть

U0 E0 4kФе f wsBm .

С другой стороны, действующее значение тока в обмотке катушки с простым магнитопроводом можно представить в виде

I Im wIm Hm I ,

kai wkai wkai

если сначала с помощью коэффициента амплитуды kai кривой тока перейти к его максимальному значению Im , а затем, пользуясь вторым законом магнитной цепи, приравнять МДС wIm обмотки к магнитному напряжению Hml по

замкнутому контуру магнитопровода.

Таким образом, напряжение U на катушке оказывается пропорциональным максимальной индукции Bm , а ток I - максимальной напряженности Hm поля в магнитопроводе. Отсюда вытекает, что вольт-амперная характеристика U F I катушки (рис. 3.16, а) должна быть подобна зависимости Bm f Hm ,

которая представляет собой основную кривую намагничивания материала магнитопровода, так как связывает координаты вершин петель гистерезиса при различных режимах его периодического перемагничивания.

Следует оговорить, что последнее заключение не совсем точно, так как при изменении режима работы катушки в общем случае меняются формы кривых тока и ЭДС катушки (по крайней мере одной из них), что приводит к изменению коэффициентов kФе и kai , то есть к нарушению строгой пропорцио-

нальности между током I и напряженностью Hm , с одной стороны, и напряжением U и индукцией Bm - с другой. Следовательно, вольт-амперная характери-

стика не будет строго подобна кривой намагничивания, хотя и останется достаточно на нее похожей.

а)

б)

в)

Рис. 3.16. Вольт-амперные характеристики U F I катушки

Своеобразной особенностью вольт-амперной характеристики ферромагнитной катушки, как впрочем и характеристик всех нелинейных элементов цепей переменного тока, является некоторая ее неопределенность. При сохранении общего характера кривой U F I , аналогичного кривой намагничивания, расположение отдельных участков характеристики данной катушки может меняться в зависимости от формы кривой тока и напряжения, при которых снималась эта характеристика. В частности, вольт-амперная характеристика1, снятая при синусоидальном напряжении (рис. 3.16, б), располагается ниже характеристики 2, полученной при синусоидальном токе в катушке. Объяснение этому явлению следует искать в закономерностях изменения коэффициентов kФе и kai , входящих в приведенные выше выражения для U и I , однако доказать указанное расхождение кривых в области насыщения магнитопровода, пользуясь

только качественной оценкой этих коэффициентов, не представляется возможным.

Эквивалентная индуктивность. Как известно, индуктивность ферромагнитной катушки в значительной степени зависит от тока. Поэтому при работе в цепи переменного тока, когда ее индуктивность в течение периода непрерывно меняется, приходится вводить понятие об эквивалентной индукщщвности, представляющей собой некоторое усредненное значение индуктивности за период. Чаще всего эквивалентную индуктивность ферромагнитной катушки в цепи переменного тока определяют по действующим значениям тока и напряжения, исходя из известных соотношений для линейных индуктивных катушек:

x L и U P x I ,

то есть оценивают выражением

LЭ x U P

I

или, пренебрегая обычно незначительным отличием реактивного напряжения U P катушки от ее полного напряжения U , формулой

L			U	.	(3.7)
	Э
			I

Обращаясь к вольт-амперной характеристике катушки (рис. 3.16, а), нетрудно убедиться, что отношение U / I изменяется при изменении режима катушки (это отношение характеризуется тангенсом угла наклона луча, проведенного из начала координат в точку на характеристике, определяющую режим). Поэтому эквивалентная индуктивность ферромагнитной катушки также не является постоянной величиной и зависит от тока или напряжения катушки.

Ферромагнитная катушка с зазором. Специфическая форма вольт-

амперной характеристики ферромагнитной катушки, показанная на рис. 3.16, а и б, характерна только для катушки без воздушного зазора. Если же в магнитопроводе ферромагнитной катушки имеется немагнитный, в частности, воздушный зазор, то такая катушка в значительном диапазоне режимов приобретает свойства практически линейного элемента цепи переменного тока и ее вольтамперная характеристика на большом участке от начала координат представляет собой прямую линию (рис. 3.16, в). Это обстоятельство становится очевидным, если вспомнить, что воздушный зазор в магнитопроводе, являясь линейным участком магнитной цепи и обычно составляя значительную долю ее сум-

марного магнитного сопротивления, приводит к спрямлению начальной части магнитной характеристики катушки. Лишь при достаточно больших токах в обмотке, когда, несмотря на воздушный зазор, наблюдается сильное насыщение магнитопровода, вольт-амперная характеристика искривляется, наклоняясь в сторону оси тока.

К устройству немагнитных зазоров в ферромагнитных катушках часто прибегают в инженерной практике, когда требуется достичь относительно высоких индуктивностей при сохранении линейности катушки, то есть при сохранении относительного постоянства ее эквивалентной индуктивности.

В условном графическом изображении ферромагнитной катушки с немагнитным зазором ее магнитопровод показывают линией с разрывом (см. рис. 3.2, в).

3.3. Анализ работы реальных катушек

Уравнение и векторная диаграмма реальной катушки. Перейдем те-

перь к анализу работы ферромагнитной катушки с учетом всех перечисленных

вп. 3.3 явлений. Обращаясь для простоты исследования к эквивалентным синусоидам тока, напряжения и ЭДС, воспользуемся вторым законом Кирхгофа для контура обмотки (рис. 3.17) и запишем в символической форме уравнение катушки:

U r0 I E0 ES ,

вкотором, наряду с основной ЭДС E0 , учтем ЭДС ES рассеяния, индуктируе-

мую в обмотке потокосцеплением рассеяния, а также падение напряжения за

счет активного сопротивления r0 обмотки.
Это уравнение, обычно записываемое в виде
U E	0	E	S	r I ,	(3.8)
				0

показывает, что приложенное к катушке напряжение U складывается из трех составляющих, первая из которых уравновешивает основную ЭДС, вторая — преодолевает ЭДС рассеяния, а третья — представляет собой падение напряжения за счет активного сопротивления обмотки.

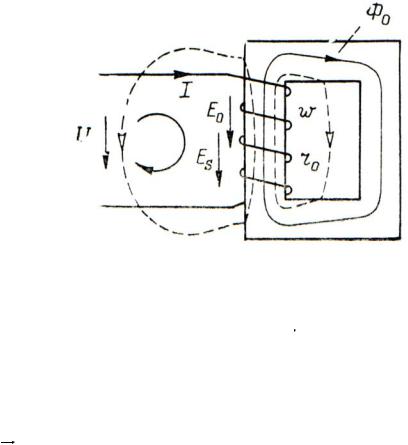
Рис. 3.17. Катушка с ферромагнитным магнитопроводом Последнее равенство наглядно иллюстрируется векторной диаграммой

катушки, построение которой начнем с вектора 0m основного магнитного потока (рис. 3.18), располагая его, как это обычно принято, горизонтально. Ориентируясь на него, построим вектор I тока в обмотке, который вследствие потерь энергии в магнитопроводе на гистерезис и вихревые токи должен опере-

жать вектор 0m на угол магнитного запаздывания. Потокосцепление ΨS рассеяния будет совпадать по фазе с создавшим его током I , так как поле рас-

сеяния в основном располагается вне магнитопровода и никаких потерь энер-

гии с этой составляющей поля не связано. Поэтому вектор ΨSm потокосцепления рассеяния будет направлен вдоль вектора I тока. Основная ЭДС и ЭДС рассеяния изобразятся векторами E0 и ES , отстающими от векторов соответст-

вующих потоков точно на 90°. Таким образом, для построения вектора U напряжения согласно уравнению катушки необходимо сложить перевернутый вектор E0 с направленным в противоположную сторону вектором ES и приба-

вить к этой сумме вектор r0 I , совпадающий по направлению с вектором тока. В выполненном построении обращаем внимание на угол между векто-

рами напряжения U и тока I , который представляет собой хорошо знакомый нам фазовый угол катушки.

Рис. 3.18. Векторная диаграмма катушки с ферромагнитным	магни-
топроводом

ЭДС и напряжение катушки. Переходя к анализу полученной векторной диаграммы (рис. 3.18), прежде всего, обратим внимание на то, что приложенное к катушке напряжение U не равно ее основной ЭДС E0 , как это имело

место в идеальной катушке. Правда, соотношения длин векторов, составляющих напряжение катушки, на рис. 3.18 из соображений наглядности векторной диаграммы несколько искажены. В действительности ЭДС рассеяния ES и па-

дение напряжения r0 I за счет активного сопротивления обмотки значительно

меньше основной ЭДС. Поэтому различие между напряжением и основной ЭДС обычно не превосходит нескольких процентов и при ориентировочных расчетах может не учитываться. Так, например, выведенные в п. 3.3 выражения для основной ЭДС в инженерной практике часто рассматриваются как приближенные выражения для напряжения ферромагнитной катушки:

U 4kФе fΨm

или

U 4,44 fwФ0m 4,44 fwsBm .

(3.9)

Таким образом, максимальный основной поток и максимальная индукция в магнитопроводе в первом приближении пропорциональны напряжению ферромагнитной катушки.

Формы кривых напряжения на катушке и ее основной ЭДС принципиально также отличаются друг от друга из-за наличия в составе напряжения и ЭДС рассеяния и падения напряжения за счет активного сопротивления обмотки, которые по форме кривой при всех условиях отличаются от основной ЭДС. Однако на практике, принимая во внимание относительную малость упомянутых слагаемых, форму кривой основной ЭДС принимают примерно совпадающей с формой кривой напряжения.

Активное сопротивление катушки. Продолжая анализировать вектор-

ную диаграмму реальной ферромагнитной катушки, спроектируем вектор напряжения U на вектор тока I (рис. 3.19, а). Полученная проекция Ua , являясь

активным напряжением катушки, по общим правилам может быть выражена через ток катушки в виде

Ua rI ,

где r - коэффициент, представляющий собой активное сопротивление катушки. Сравнивая последний вектор с расположенным в верхней части диаграммы вектором r0 I падения напряжения за счет активного сопротивления обмот-

ки, нетрудно убедиться, что первый из названных векторов длиннее второго, то есть

rI r0 I ,

и, следовательно,

r r0 .

Рис. 3.19. Векторные диаграммы катушки с ферромагнитным	маг-
нитопроводом

Таким образом, для ферромагнитной катушки существуют два различающихся понятия активного сопротивления катушки и активного сопротивления обмотки, причем первое больше второго. Понятие активного сопротивления обмотки нам уже знакомо. Это коэффициент, который определяет мощность, затрачиваемую на нагрев обмотки протекающим по ней током:

P0 r0 I 2 .

При низкой частоте и тонком проводе, из которого выполнена обмотка, то есть в случае, когда можно пренебречь явлением поверхностного эффекта, активное сопротивление r0 обмотки не отличается от сопротивления R0 этой об-

мотки постоянному току ( r0 R0 ).

Активное сопротивление r катушки в целом по общему определению этого понятия является отношением мощности P , расходуемой в катушке, к квадрату тока:

r IP2 .

В ферромагнитной катушке мощность складывается из двух составляющих: только что упомянутой мощности P0 , определяющей нагрев обмотки, и

мощности PM магнитных потерь катушки, то есть потерь в ее магнитопроводе

на гистерезис и вихревые токи. Поэтому для активного сопротивления катушки имеем

r	P	P0	PM r		PM ,
	I 2		I 2	0	I 2

то есть активное сопротивление катушки включает в себя активное сопротивление обмотки, но содержит в себе еще одно слагаемое, определяемое мощностью магнитных потерь катушки.

Заметим, что обычно активное сопротивление катушки оказывается много больше активного сопротивления обмотки, иногда превышая его в десятки раз.

Индуктивность и сопротивление рассеяния. Как уже упоминалось вы-

ше, потокосцепление рассеяния ΨS пропорционально току. Поэтому для мгновенных значений этих величин можно записать выражение

ΨS LS i ,

в котором коэффициент LS получил название индуктивности рассеяния катуш-

ки.

Подчеркнем, что эту величину не следует путать с понятием индуктивности катушки в целом, которая значительно больше индуктивности рассеяния, так как определяется суммарным потокосцеплением обмотки, основную долю которого составляет потокосцепление Ψ0 , связанное с основным потоком Φ0 в

магнитопроводе известной зависимостью

0 =wΦ0 .

Используя введенное понятие индуктивности рассеяния, для мгновенного значения ЭДС рассеяния можно написать:

eS ddΨtS LS dd ti .

Переходя к символической записи этого равенства, получим

ES j LS I jxS I ,

где величина

xS LS

представляет собой индуктивное сопротивление рассеяния катушки. Поэтому вектор ES на векторной диаграмме (см. рис. 3.18) можно символически записать комплексным числом

ES jxS I U S ,

формально представляющим падение напряжения в катушке за счет индуктивного сопротивления рассеяния. Как и всякий вектор напряжения на идеальном

индуктивном элементе, вектор xS I ES (см. вариант диаграммы на рис. 3.19,

б) опережает вектор тока I на 90°.

Разложение тока катушки. В ряде случаев оказывается целесообразным разложить вектор тока в катушке на две взаимно-перпендикулярные составляющие, как это было сделано ранее для случая идеальной ферромагнитной катушки. Показанные на рис. 3.19, б составляющие I и I тока по-прежнему назы-

вают соответственно активным и реактивным токами, однако для реальной ферромагнитной катушки эти названия следует понимать условно, так как вектор первой составляющей теперь не совпадает по направлению с вектором напряжения катушки, а вектор второй – ему не перпендикулярен. Поэтому эти величины не подходят под строгие определения активного и реактивного токов.

Эквивалентная схема. Для ферромагнитной катушки можно составить эквивалентную схему, приведенную на рис. 3.20 и включающую четыре идеальных элемента — два резистора и две катушки. Каждый из этих элементов отражает определенное явление в катушке. Например, резистор r0 , сопротивле-

ние которого выбирают равным активному сопротивлению обмотки, служит для воспроизведения эффекта нагревания обмотки протекающим по ней током

I .

Магнитное поле рассеяния реальной катушки отражают в эквивалентной схеме катушкой LS , для чего ее индуктивность принимают равной индуктивно-

сти рессеяния реальной ферромагнитной катушки. Контур L0 , gM предназначен для учета физических явлений в магнитопроводе. В частности, с помощью катушки L0 воспроизводят основной магнитный поток реальной катушки, и, следовательно, ее индуктивность подчиняют условию

E0 L0 I ,

то есть чтобы в этой катушке реактивная составляющая I тока индуктировала ЭДС E0 , равную основной ЭДС катушки.

Резистором gM учитывают потери энергии в магнитопроводе на гистере-

зис и вихревые токи. Для этого проводимость резистора должна быть такой, чтобы выделяемая в нем мощность равнялась мощности потерь в магнитопроводе:

gM U02 PM .

Следует особо оговорить, что названные выше параметры r0 , LS , L0 и gM

элементов эквивалентной схемы вследствие нелинейности ферромагнитной катушки не являются постоянными величинами и изменяются при изменении режима работы катушки, в частности, в зависимости от приложенного к ней напряжения. В первую очередь это относится к индуктивности L0 и проводимо-

сти gM , которые для данной катушки могут изменяться в очень широких пределах.

r0

Рис. 3.20. Эквивалентная схема реальной катушки

Доказательство эквивалентности схемы и реальной катушки Не-

трудно проверить, что уравнение, записанное по второму закону Кирхгофа для основного контура эквивалентной схемы (рис. 3.20)

U U0 US r0 I 0

или

U U0 US r0 I ,

совпадает с уравнением (3.8) катушки, если принять во внимание, принятое ранее обозначение US ES , дополненное условием U0 E0 .

Это совпадение и свидетельствует об эквивалентности рассмотренной схемы реальной катушке, то есть о возможности замены катушки цепью из идеальных элементов, соединенных по схеме рис. 3.20, без нарушения режима в остальной части той цепи, где была включена ферромагнитная катушка.

Справедливой для эквивалентной схемы остается и векторная диаграмма катушки. Например, диаграмму, представленную на рис. 3.19, б с точки зрения эквивалентной схемы можно трактовать следующим образом. Если за исход-

ный вектор принять вектор напряжения U0 , то ток I в идеальной катушке L0 (рис. 3.20) будет отставать от приложенного к ней напряжения U0 на 90°, а ток I в идеальном резисторе gM — совпадать с ним по фазе. Сумма этих токов равна току I в неразветвленной части эквивалентной схемы. Напряжение U питания цепи складывается из трех напряжений: U0 , US xS I и Ur r0 I , второе

из которых, как и напряжение на идеальной катушке, опережает ток на 90°, а третье, являясь напряжением на идеальном резисторе, совпадает с током.

3.4.Потери в магнитопроводах

Опотерях энергии в магнитопроводе. Переходя к более подробному рассмотрению вопроса о потерях энергии в магнитопроводе, обратим внимание на его исключительную важность для практической электротехники. Помимо того, что эти потери ведут к снижению коэффициента полезного действия электротехнических устройств, они вызывают нагрев магнитопровода. Это резко осложняет эксплуатацию оборудования, требуя специальных мер для охлаждения магнитопроводов, а в некоторых случаях приводит к аварийным ситуациям, полностью выводящим оборудование из строя. Поэтому инженеры как в процессе конструирования электротехнических устройств, так и при их эксплуатации всегда стремятся к уменьшению этих потерь, что возможно лишь на основе глубокого понимания природы их возникновения.

Потери на гистерезис. Обратимся сначала к потерям, вызванным в магнитопроводе явлением гистерезиса. Потери, как правило, рассчитываются по эмпирической формуле Штейнмеца:

WГ Bmn ,

(3.10)

определяющая удельные потери энергии на гистерезис в единице объема материала за один цикл его перемагничивания по симметричной петле с максимальной индукцией Bm . Напомним, что фигурирующие в формуле коэффициенты и n определяются физико-химическими свойствами материала, а показатель степени n к тому же зависит еще и от максимальной индукции Bm , принимая

значения в пределах от 1,6 до 2.

При работе катушки в цепи переменного тока ее магнитопровод претерпевает периодические перемагничивания с частотой f . Это значит, что удель-

ные потери энергии в единицу времени, то есть удельная мощность потерь на гистерезис будет равна

PГ WГ f

или
PГ Bmn f .	(3.11)

Таким образом, удельная мощность потерь на гистерезис пропорциональна частоте и максимальной индукции в степени n ( n 1,6 2 ).

Мощность потерь на гистерезис во всем магнитопроводе можно рассчитать по удельной мощности, используя очевидное соотношение

PГ PГ v ,

где v — объем магнитопровода.

Удельная энергия, затрачиваемая на перемагничивание материала, обладающего гистерезисом, определяется площадью петли гистерезиса. Поэтому проблема уменьшения потерь на гистерезис сводится к разработке ферромагнитных материалов с наименьшей площадью этой петли и решается главным образом физиками и металлургами. На долю электриков в этом отношении падает задача лишь оптимального выбора условий эксплуатации ( Bm и f ) магни-

топровода, обеспечивающих достаточно эффективное его использование при ограниченных потерях на гистерезис.

Потери на вихревые токи связаны с нагреванием магнитопровода вихревыми токами, и поэтому мощность этих потерь согласно формуле

P R I 2

для мощности, расходуемой на нагревание резистора с сопротивлением R протекающим по нему током I , будет пропорциональна квадрату вихревого тока и, следовательно, квадрату индуктирующейся в магнитопроводе вихревой ЭДС. Поскольку же ЭДС индукции, в свою очередь, согласно формуле

E 4kФ f ws Bm

пропорциональна частоте f и максимальной индукции Bm , можно утверждать,

что мощность потерь на вихревые токи будет пропорциональна квадрату этих величин. В частности, для удельной мощности потерь на вихревые токи можно написать:

PB Bm2 f 2 ,

(3.12)

где - коэффициент, зависящий от удельной электрической проводимости материала магнитопровода и его конструкции.

Мощность потерь на вихревые токи во всем магнитопроводе рассчитывают по удельной мощности потерь и объему v магнитопровода, пользуясь соотношением

PB PB v .

Зависимость потерь на вихревые токи от удельной электрической проводимости материала магнитопровода нетрудно рассчитать, опираясь на хорошо известное выражение для мощности:

P GU 2 ,

расходуемой в резисторе с проводимостью G. Так как электрическая проводимость путей, по которым замыкаются вихревые токи в магнитопроводе, пропорциональна удельной электрической проводимости его материала, то пропорциональной этой проводимости окажется и мощность потерь на вихревые токи.

Поэтому в целях уменьшения потерь на вихревые токи разработчики магнитных материалов всегда стремятся к уменьшению их удельной проводимости, что достигается, например, в углеродистых сталях присадкой к ним довольно большого количества кремния (до 4 %).

Резкого сокращения потерь на вихревые токи удается достичь в магнитопроводах из ферритов — магнитных материалов, обладающих электрическими свойствами полупроводников, то есть имеющих весьма высокое удельное сопротивление или, что то же самое, ничтожную удельную проводимость.

Расслоение магнитопроводов. Из конструктивных мер, сказывающихся на уменьшении потерь от вихревых токов, решающее значение имеет расслоение магнитопровода, то есть изготовление его не сплошным (рис. 3.21, а), а в виде пакета электрически изолированных друг от друга тонких листов ферромагнитного материала (рис. 3.21, б). Если отдельные листы располагать в пакете магнитопровода так, чтобы их плоскости были направлены вдоль магнитных линий, то расслоение магнитопровода практически не повлияет на его магнитное сопротивление. Для вихревых же токов, показанных на рис. 3.21 штриховыми линиями и замыкающихся в плоскостях, перпендикулярных к вектору магнитной индукции В, изоляционные промежутки между тистами окажутся непреодолимым препятствием, и эти токи будут вынуждены замыкаться лишь в пределах поперечного сечения каждого листа (рис. 3.21, б). Нетрудно убедиться, что величина вихревых токов при этом уменьшится, что приведет к снижению потерь на вихревые токи. В самом деле, вихревой ток, замыкающийся

внутри трубки электрического тока небольшого поперечного сечения пропорционален ЭДС, индуктирующейся в контуре этой трубки, и обратно пропорционален ее сопротивлению. Сравним два тока, замыкающихся по периферийным трубкам одинакового сечения в теле сплошного магнитопровода квадратного поперечного сечения (рис. 3.21, а) и в теле одного листа расслоенного магнитопровода (рис. 3.21, б). Обратим внимание, что выбранные токи будут являться наибольшими в пределах каждого магнитопровода, так как их контуры охватывают наибольшие магнитные потоки и, следовательно, в этих контурах будут индуктироваться наибольшие вихревые ЭДС. Предположив, что второй магнитопровод разделен на 100 слоев, мы должны согласиться, что наибольшая вихревая ЭДС в нем будет в 100 раз меньше наибольшей вихревой ЭДС в первом случае, так как магнитный поток одного листа будет в 100 раз меньше потока всего магнитопровода. Сопротивление же трубок тока в расслоенном магнитопроводе упадет не более чем в два раза по сравнению со сплошным магнитопроводом, так как длина пути периферийной трубки тока в листе будет в первом приближении равняться двум сторонам квадрата сечения магнитопровода, в то время как в сплошном магнитопроводе она равна четырем сторонам. Таким образом, наибольший вихревой ток в расслоенном магнитопроводе окажется в 50 раз меньше наибольшего тока сплошного магнитопровода.

Более строгий расчет мощности потерь на вихревые токи, приводимый в следующем пункте, подтверждая справедливость только что проделанных грубых прикидок, показывает, что эта мощность пропорциональна квадрату толщины пластин. Вот почему по мере повышения частоты магнитопровод приходится изготовлять из все более тонких пластин. Например, при промышленной частоте 50 Гц обычно применяют листовую электротехническую сталь толщиной 0,5 1 мм, при повышенной частоте 400 Гц толщину листов уменьшают до 0,2 0,35 мм, а в технике звуковых частот переходят к весьма тонким лентам (до сотой доли миллиметра).

б)

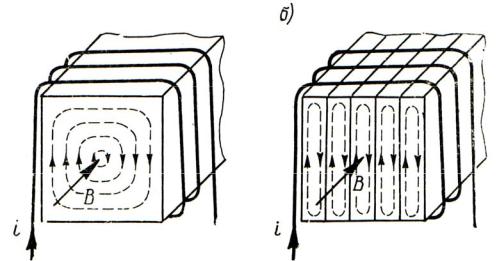
а)

Рис. 3.21. Способы изготовления магнитопровода

Расчет удельных потерь на вихревые токи. Подсчитаем мощность по-

терь в одном листе магнитопровода толщиной d , высотой h и длиной l (рис. 3.22), полагая, что магнитное поле направлено по длине листа. В этом случае вихревые токи замыкаются по контурам в плоскостях d h поперечного сечения листа. Выделим из всего объема этого листа элементарную трубку тока в виде ремня толщиной d x , шириной во всю длину l листа, и проходящую на

расстоянии x по обе стороны от его осевой линии.

Опираясь на известную формулу мощности цепи переменного тока

P U 2 g ,

составим выражение для мощности потерь от вихревого тока в пределах выбранной элементарной трубки. Активную проводимость трубки можно принять равной ее проводимости постоянному току и подсчитать через длину lT и пло-

щадь sT поперечного сечения трубки, ориентируясь на известное выражение

g G	1		1			sT	,
	R			lT
						l
			s			T

T

где и — соответственно удельное сопротивление и удельная проводимость материала листа.

В нашем случае площадь поперечного сечения трубки тока (на рис. 3.22 эта площадь отмечена горизонтальной штриховкой) бесконечно мала, так как бесконечно малой принята толщина трубки d x . Длину lT трубки тока в листах,

где h d , можно приближенно принять равной двум высотам листа (см. рис. 3.22)

lT 2h ,

и, следовательно, для активной проводимости трубки, которая также будет бесконечно малой, получим

d g l2dhx .

Напряжение U, фигурирующее в приведенной выше формуле мощности, в нашей задаче представляет собой напряжение вдоль всей замкнутой трубки тока, равное, как известно, ЭДС Е, действующей в контуре трубки, то есть ЭДС, индуктируемой сцепленным с контуром магнитным потоком. Для действующего значения этой ЭДС имеем

E 4kФ f ws Bm

или, поскольку трубка тока является одновитковым контуром (w = 1),

E 4 kФ f s Bm

При этом под площадью s следует понимать часть площади поперечного сечения листа, охватываемую контуром трубки вихревого тока (на рис. 3.22 эта площадь отмечена косой штриховкой). Приближенно эту площадь можно оценить произведением

s h 2x .

Тогда для ЭДС Е имеем

E8kФ f h x Bm

идля мощности, расходуемой в объеме элементарной трубки тока, получим

d PB E2d g 64kФ2 f 2 Bm2 h2 x2 l2dhx 32kФ2 f 2 Bm2 hl x2 d x .

Рис. 3.22. Схема электротехнической стали, используемой	в
слоистом магнитопроводе

Мощность, расходуемую на нагрев вихревыми токами всего листа в целом, найдем, суммируя мощности во всех трубках вихревого тока, плотно вложенных одна в другую и заполняющих весь объем листа. Математически эта операция эквивалентна интегрированию выражения для d PB в пределах от

x 0 до x d / 2 , то есть начиная от самой узкой трубки, примыкающей к осевой линии листа и кончая самой широкой трубкой, располагающейся у поверхности листа,

	d / 2	2	2	2	2	2	2	1	d			3		4	2	2	2	3
PB	2																		.
	32kФ f		Bm hl x		d x 32kФ f		Bm hl	3		2				3	kФ f		Bm hl d
	0

Принимая во внимание, что объем листа выражается произведением трех его размеров:

v h l d ,

от только что полученного выражения нетрудно перейти к формуле для удельной мощности потерь на вихревые токи в расслоенном магнитопроводе:

PB PvB 43 kФ2 f 2 Bm2 d 2 .

Эта формула подтверждает выводы, полученные в предыдущем пункте относительно зависимости удельных потерь на вихревые токи от удельной проводимости материала магнитопровода, максимальной индукции Bm в нем, а

также от частоты f тока в катушке. Кроме того, формула показывает, что по-

тери на вихревые токи возрастают с квадратом толщины d листов, из которых собран магнитопровод.

Допущенные приближения. Следует оговорить, что проведенный вывод удельных потерь на вихревые токи является приближенным и не только потому, что в нем допускалось неточное определение длины lT трубки и охваты-

ваемой ею площади s поперечного сечения листа. При выводе предполагалось также, что магнитная индукция в пределах поперечного сечения листа оставалась неизменной. Только в этом случае справедливы простое выражение Фm Bm s для магнитного потока магнитопровода и вытекающая из него фор-

мула для ЭДС:

E 4kФ f ws Bm ,

положенная в основу рассмотренного вывода.

Строго же говоря, магнитная индукция не остается одинаковой по поперечному сечению листа. Под влиянием поверхностного эффекта она уменьшается от поверхности в глубь листа.

О поверхностном эффекте в магнитопроводах. Как известно, поверх-

ностный эффект в электрических проводах заключается в том, что переменный ток неравномерно распределяется по поперечному сечению провода: в поверхностном слое провода плотность тока больше, а в центральной области меньше.

Аналогичное явление в отношении магнитного потока при переменном магнитном поле наблюдается и в сплошных магнитопроводах: магнитная индукция, то есть плотность магнитного потока, приобретает наибольшее значение у поверхности магнитопровода, ослабевая к середине его поперечного сечения. Причиной такого эффекта, называемого магнитным поверхностным эффектом, являются вихревые токи, индуктирующиеся в теле магнитопровода. Как всякие токи, они порождают собственное магнитное поле, которое по правилу Ленца противодействует причине, вызывающей эти вихревые токи, то есть ослабляет основное поле магнитопровода. Обращаясь к картине вихревых токов в сплошном магнитопроводе (см. рис. 3.21, а), нетрудно убедиться, что с центральной магнитной линией сцепляется весь вихревой ток; магнитные же линии, проходящие дальше от центра, охвачены лишь долью всего вихревого

тока и тем меньшей, чем ближе расположены линии к поверхности магнитопровода. Поэтому в центре сечения магнитопровода ослабление основного поля вихревыми токами будет сказываться наиболее сильно. Наоборот, на поверхности магнитопровода основное поле совершенно не будет ослаблено.

Как и в электрических проводах, яркость проявления магнитного поверхностного эффекта зависит от частоты, возрастая с ее увеличением.

В расслоенном магнитопроводе магнитный поверхностный эффект наблюдается лишь в пределах данного листа, проявляясь значительно слабее, чем в сплошном магнитопроводе. Поэтому в относительно тонких листах при сравнительно низких частотах этим явлением можно пренебречь, что и было сделано при выводе потерь на вихревые токи в предыдущем пункте.

Полные потери в магнитопроводе. Прежде всего подчеркнем, что, об-

ращаясь к потерям в магнитопроводах, следует четко различать три рассмотренных выше понятия, обычно объединяемых общим названием магнитные потери: потери энергии, мощность потерь и удельную мощность потерь. Первая из этих величин оценивает энергию, затраченную на нагревание магнитопровода за определенный отрезок времени. Вторая —отражает интенсивность процесса выделения тепла в магнитопроводе в данный момент времени, а третья — является одной из важнейших характеристик магнитного материала при его использовании в переменных магнитных полях. О каждой из этих величин можно говорить, касаясь только потерь на гистерезис, или только потерь на вихревые токи, или рассматривая полные потери, складывающиеся из двух упомянутых составляющих. В частности, для наиболее широко используемого на практике понятия удельной мощности потерь имеем

PM PГ РВ .

Напомним, что понятие удельной мощности потерь мы определили ранее как отношение мощности РМ потерь во всем магнитопроводе к его объему v :

PM PvM ,

измеряемое в ваттах на кубический метр (Вт/м3 ).

В инженерной же практике вместо этого широко используемого в теоретической электротехнике понятия, предпочитают пользоваться мощностью потерь, отнесенной не к объему, а к массе магнитопровода:

PM PmM ,

также называемой удельной мощностью потерь, но измеряемой в ваттах на килограмм (Вт/кг).

Очевидно, что оба понятия легко связываются друг с другом соотноше-

нием

PM v PM m ,

вытекающим из равенства потерь в данном магнитопроводе объемом v и массой m , подсчитанных через удельные мощности PM и PM . Отсюда для вычис-

ления удельной мощности PM по удельной мощности PM получим

PM Pm mv PM ,

где - плотность материала магнитопровода, равная отношению

mv

массы магнитопровода к его объему.

Разделение потерь. При испытаниях ферромагнитных материалов удается измерить только полные магнитные потери, хотя в ряде случаев необходимо отдельно знать и их доли, то есть потери на гистерезис и потери на вихревые токи. Отсюда и возникает задача о разделении магнитных потерь, решение которой становится возможным благодаря тому, что потери на гистерезис пропорциональны первой степени частоты, а потери на вихревые токи пропорциональны квадрату частоты.

Обращаясь к выражениям (3.11) и (3.12) для удельной мощности потерь на гистерезис и вихревые токи, составим из них удельную мощность полных магнитных потерь:

			2	2		2
PM	PГ	PB	Bm f Bm f
b разделим ее на частоту f
					f	/
PM	PГ	PB Bm B2
f	f	f	n	m

Полученное выражение показывает, что отношение полных потерь к частоте представляет собой линейную функцию частоты. Поэтому если измерить удельную мощность полных потерь при нескольких частотах, сохраняя неизменной максимальную индукцию Bm , и построить по этим данным график за-

висимости отношения PM / f от частоты, то он представит собой прямую линию (рис. 3.23), отсекающую на оси ординат отрезок

Bmn PfГ ,

равный отношению потерь на гистерезис к частоте. Разность же ординат построенной прямой и ее начальной ординаты при любой частоте будет равна отношению PB / f потерь на вихревые токи к этой частоте.

Таким образом, рассмотренное графическое построение позволяет раздельно определить отношения PГ / f и PB / f для любой интересующей нас

частоты, умножив которые на частоту f, мы получим и сами составляющие PГ и PB полных потерь.

Естественно, что задача о разделении потерь может быть решена и чисто аналитически, если будут достоверно известны полные потери при двух разных частотах, но одинаковых максимальных индукциях

Рис. 3.23. Разделение потерь в магнитопроводе

.

3.5. Ферромагнитные катушки с подмагничиванием

Устройство и назначение катушек. Ферромагнитная катушка с иод-

магничиванием представляет собой индуктивную катушку, на магнитопроводе которой име.тся две обмотки (рис. 3.24), одна из которых, называемая рабочей обмоткой, предназначена для включения в цепь переменного тока, а вторая, именуемая обмоткой подмагничивания, питается от источника постоянного тока.

Катушки с подмагничиванием используются в цепях переменного тока в качестве катушек с переменной индуктивностью. Однако в отличие от предназначенных для тех же целей катушек с раздвижным маг-нитопроводом изменение индуктивности этих катушек достигается без всяких движущихся частей

только за счет изменения постоянного тока в обмотке подмагничивания. В этом заключается их существенное преимущество перед катушками с раздвижным магнитопроводом, позволяющее широко использовать эти катушки в автоматических устройствах управления и регулирования.

Предупредим, что катушку с подмагничиванием, несмотря на наличие в ней двух обмоток, не следует отождествлять с трансформатором, поскольку обмотка подмагничивания ставится в такой режим работы, когда передачи энергии из одной цепи в другую не происходит.

Рис. 3.24. Индуктивная катушка с подмагничиванием

Зависимость индуктивности катушки от тока подмагничивания ус-

тановим для понятия эквивалентной индуктивности ферромагнитной катушки в цепи переменного тока:

LЭ xL U ,

I

где в рассматриваемом случае U представляет собой действующее напряжение на рабочей обмотке, а I — ток в ней, называемый рабочим током катушки.

Напряжение на катушке по величине мало отличается от ее основной ЭДС, для действующего значения Е которой согласно выражению (3.1) имеем

E kФECP kФ 2ΔΨ f 2kФ w Ф f ,

где — размах колебаний потокосцепления рабочей обмотки; w— число ее витков; Φ — размах колебаний потока в магнитопроводе.

Таким образом, для индуктивности рабочей обмотки имеем

	L	U		E		2kΦw Φf	kФ w Φ .
		I		I
	Э					2 f I	I

Последнее равенство показывает, что если катушку поставить в режим работы при неизменном рабочем токе I , то индуктивность рабочей обмотки легко оценить по размаху Φ колебаний потока магнитопровода.

Обратимся теперь к магнитной характеристике Φ f F магнитопровода,

связывающей его магнитный поток Ф и результирующую МДС F расположенных на нем обмоток (рис. 3.25). Очевидно, что в рассматриваемом случае мгновенное значение этой МДС можно представить суммой

F FP FП

мгновенной МДС рабочей обмотки

FP wi ,

и МДС обмотки подмагничивания

FП wП I П ,

где i – мгновенный рабочий ток; wП – число витков обмотки подмагничивания; I П – постоянный ток в ней, называемый током подмагничивания.

Рассмотрим для наглядности три режима подмагничивания, в первом из которых ток I П подмагничивания примем равным нулю (отсутствие подмагничивания). В этом случае на магнитопровод будет действовать только рабочая обмотка, и он при синусоидальной МДС FP будет претерпевать симметричные

перемагничивания в пределах крутого прямолинейного участка магнитной характеристики (см. левую часть построений на рис. 3.25). При этом сравнительно небольшой амплитуде FPm w Im рабочей МДС, то есть небольшому рабо-

чему току, будет соответствовать большой размах колебаний магнитного потока.

Во втором случае, когда ток подмагничивания равен некоторой величине I П , определяющей соответствующее значение МДС подмагничивания

FП wП I П , магнитопровод будет подвержен действию двух обмоток и колебания магнитного потока можно будет найти по колебаниям результирующей МДС F FP FП (см. среднюю часть построений на рис. 3.25) . Так как током

подмагничивания магнитный режим магнитопровода выведен в область пологой части магнитной характеристики, та же переменная составляющая МДС рабочей обмотки (напомним, что мы условились рассматривать режимы при неизменной амплитуде Im рабочего тока) вызывает значительно меньший размах

Φ колебаний магнитного потока, что свидетельствует о резком уменьшении эквивалентной индуктивности катушки по сравнению с первым режимом.

Дальнейшие увеличения тока I П , а следовательно, и МДС FП подмагничивания до значения FП (см. правую часть построений на рис. 3.25) повлекут

дальнейшее снижение размаха Ф колебаний магнитного потока, а значит, снижение индуктивности.

Рис. 3.25. Магнитная характеристика индуктивной катушки	с
подмагничиванием

В результате при неизменном рабочем токе в катушке наблюдается представленная на рис. 3.26 зависимость ее индуктивности от тока подмагничивания.

Рис. 3.26. Зависимость индуктивности катушки от тока подмагничивания

Качественно аналогичная зависимость индуктивности катушки от тока подмагничивания наблюдается и в любом другом режиме катушки, в частности

врежиме неизменного напряжения U на ее рабочей обмотке.

Очетных гармониках в катушках с подмагничиванием. Как во всяких ферромагнитных катушках, в катушках с подмагничиванием имеют место искажения форм кривых напряжения и тока. Однако наличие постоянного подмагничивания вносит некоторые особенности в эти явления.

Рис. 3.27. Подмагничивание магнитопровода индуктивной катушки двумя обмотками

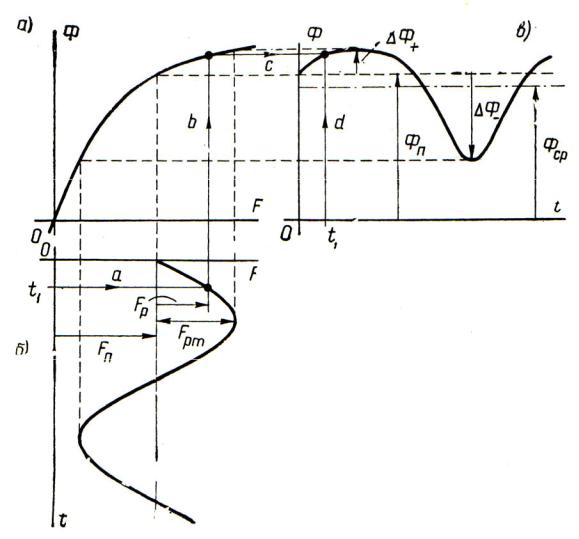
Остановимся подробнее на рассмотренном в предыдущем пункте режиме местного намагничивания магнитопровода (см. рис. 3.24) двумя обмотками, полагая для определенности рабочий ток i и, следовательно, МДС FP рабочей обмотки синусоидальными. Для этого совместим на одном рисунке магнитную

характеристику магнитопровода (рис. 3.27, а) с временной диаграммой результирующей МДС обеих обмоток:

F FP FП

(рнс. 3.27, б) и, пользуясь построениями, выполненными в качестве примера на этом рисунке для момента времени t1 (см. операции a, b, c, d ), определим кри-

вую зависимости потока Ф магнитопровода от времени (рис. 3.27, в). Нетрудно убедиться, что вследствие явления насыщения магнитопровода наибольшее приращение Ф+ магнитного потока над его значением ФП, соответствующим действию только одной постоянной м.д. с. FП (рис. 3.27, б), будет по абсолютному значению меньше наибольшего приращения Φ за время отрицательной

полуволны рабочей МДС. В результате среднее значение ΦСР магнитного потока за период, или, иначе говоря, его постоянная составляющая (на рис. 3.27, б она отмечена штрих-пунктирной линией), окажется меньше величины ΦП , а

переменная составляющая потока (она изображается той же кривой, но рассматриваемой относительно штрих-пунктирной оси) будет несимметрична относительно оси времени (отдельно кривая переменной составляющей пото-

ка представлена на рис. 3.28). Несимметричными относительно оси времени будут и кривые ЭДС e , индуктирующихся в обмотках, в частности кривая ЭДС в рабочей обмотке, построенная на рис. 3.28. Поэтому несимметричным окажется и напряжение на рабочей обмотке катушки.

Рис. 3.28. Кривая ЭДС в рабочей обмотке индуктивной катушки

Эта несимметрия означает, что в разложении кривых ЭДС и напряжения ферромагнитной катушки при подмагничивании постоянным током, наряду с

нечетными, присутствуют также и четные гармоники (вторая, четвертая, шестая и т. д.). Если аналогичным образом проанализировать работу катушки с подмагничиванием в режиме ее работы при синусоидальном напряжении на рабочей обмотке, и, следовательно, при синусоидальной переменной составляющей магнитного потока, то можно прийти к выводу, что в этом случае четные гармоники появятся в кривой рабочего тока.

Возникновение четных гармоник в кривых напряжения и тока является специфической особенностью ферромагнитных катушек с подмагничиванием.

Вольт-амперные характеристики катушки. Важную роль при оценке режима работы катушки с подмагничиванием в цепи переменного тока играют ее вольт-амперные характеристики, представляющие собой своеобразное семейство зависимостей U f I напряжения U на рабочей обмотке от рабочего

тока I при различных токах подмагничивания (рис. 3.29). Естественно, что вольт-амперная характеристика катушки при отсутствии подмагничивания, то есть когда I П 0 (кривая 1 на рис. 3.29), не будет отличаться от вольт-

амперной характеристики обычной ферромагнитной катушки (рис. 3.12, а). Однако при наличии подмагничивания эти характеристики изменяются, приобретая характерную S-образную форму. При этом, чем больше ток подмагничивания, тем дальше от оси ординат смещается крутой участок характеристики

(кривые 2, 3, 4, 5 на рис. 3.29).

Объяснение вольт-амперных характеристик. Для того чтобы понять причину имеющего место изменения вольт-амперных характеристик катушки под влиянием подмагничивания, обратимся к магнитной характеристике Φ f F магнитопровода катушки (рис. 3.30, а). Полагая ток IП подмагничи-

вания, а вместе с ним и МДС FП неизменными, предположим, что рабочий ток i , а соответственно и рабочая МДС FP , являясь синусоидальными функциями времени, по амплитуде монотонно возрастают (рис. 3.30, б).

Рис. 3.29. Вольт-амперные характеристики индуктивной катушки при различных токах подмагничивания

Рис. 3.30. Магнитная характеристика Φ f F магнитопровода катушки

Пока амплитуда FPm рабочей МДС невелика и колебания результирующей МДС ограничены областью насыщения характеристики магнитопровода,

соответствующие колебания магнитного потока возрастают с увеличением рабочего тока незначительно (рис. 3.30, в). Этому соответствует незначительное возрастание напряжения U на рабочей обмотке, то есть относительно пологая начальная часть 0 a вольт-амперной характеристики катушки (см. рис. 3.29). При дальнейшем увеличении рабочего тока, когда минимальные значения результирующей МДС (на рис. 3.30, б — левые вершины синусоиды МДС FP )

выходят на крутой участок магнитной характеристики, незначительному увеличению FPm будет соответствовать резкое возрастание размаха ΔΦ колебаний

магнитного потока (рис. 3.30, б). Это и повлечет за собой крутой подъем вольтамперной характеристики на участке а б (рис. 3.29). Когда же рабочий ток возрастет настолько, что амплитуда FPm рабочей МДС превысит МДС FП

подмагничивания и минимальные значения результирующей МДС достигнут колена магнитной характеристики в ее отрицательной области (рис. 3.30, б), дальнейшее возрастание FPm уже не вызовет существенного увеличения Ф,

так как и максимум, и минимум результирующей МДС соответствуют насыщенному состоянию магнитопровода. Эти режимы отвечают верхней пологой части вольт-амперной характеристики катушки (правее точки б на рис. 3.29).

Нетрудно убедиться, что с увеличением тока подмагничивания, то есть с возрастанием МДС FП , крутая часть вольт-амперной характеристики будет пе-

ремещаться в область больших значений рабочего тока I , как и показано на рис. 3.29.

3.6. Управляемые реакторы.

Простейшая конструкция ферромагнитной катушки с подмагничиванием, описанная ранее (рис. 3.24), практически не позволяет обеспечить надлежащего режима ее работы. Это объясняется тем, что переменное поле магнитопровода индуктирует в обмотке подмагничивания ЭДС, вызывающую в цепи подмагничивания переменную составляющую тока, которая согласно принципу Ленца оказывает размагничивающее действие на магнитопровод. Последнее приводит к резкому снижению эквивалентной индуктивности рабочей обмотки, не связанному с подмагничиванием магнитопровода постоянным током, и, следовательно, к нарушению закономерностей описанных выше явлений.

Нормальное функционирование простейшего варианта катушки с подмагничиванием (см. рис. 3.24) станет возможным лишь в том случае, если в цепь подмагничивания включить дополнительную катушку Ld (рис. 3.31) с

достаточно большой индуктивностью. Не являясь заметным препятствием для постоянного тока подмагничивания, такая катушка окажет значительное сопротивление для переменной составляющей тока.

Рис. 3.31. Индуктивная катушка с подмагничиванием и дополнительной индуктивностью Ld

Однако практически более целесообразным решением вопроса является использование двух одинаковых катушек с подмагничиванием, соединенных на стороне переменного тока или последовательно (рис. 3.32, а), или параллельно

(рис. 3.22, б).

а)	б)	в)

Рис. 3.32. Схемы двух одинаковых катушек с подмагничиванием

Обмотки же подмагничивания этих катушек в обоих случаях включают встречно-последовательно, то есть так, чтобы индуктирующиеся в них переменные ЭДС e были направлены в контуре подмагничивания навстречу друг

другу (рис. 3.32, б) и поэтому взаимно компенсировались. При этом каждая катушка, взятая в отдельности, будет работать в описанных выше режимах, так как изменение направления тока подмагничивания в одной из них не меняет

существа дела. В целом же, по отношению к паре катушек цепь подмагничивания уже не будет играть роль размагничивающего замкнутого контура.

Тот же эффект может быть достигнут объединением двух катушек в одну магнитную систему путем устройства одной обмотки подмагничивания, охватывающей сразу два магнитопровода (рис. 3.33, а). Необходимо только соединить рабочие обмотки w двух магнитопроводов так, чтобы магнитные поля, созданные рабочим током i в каждом из магнитопроводов, были направлены внутри обмотки wП подмагничивания в противоположные стороны и таким

образом компенсировали друг друга.

Развитие этой идеи приводит к катушке с трехстержневым магнитопроводом (рис. 3.33, б), в котором переменное магнитное поле Φ , созданное рабочими обмотками, замыкается по крайним стержням, вообще не заходя в средний стержень, где существует только поле ΦП постоянного подмагничива-

ния.

Естественно, что в обоих последних вариантах сдвоенной катушки с подмагничиванием рабочие обмотки могут быть соединены не только последовательно, как показано на рис. 3.33, но и параллельно.

Такие сдвоенные (электрически или магнитно) катушки с подмагничиванием называют управляемыми реакторами, или дросселями насыщения. При графическом изображении управляемых реакторов в электрических схемах обычно показывают только по одной обмотке в цепях переменного и постоянного токов (рис. 3.34). Однако с целью отличия условного обозначения управляемого реактора от обозначения трансформатора в первом случае черту, обозначающую магнитопровод, располагают не вдоль осей обмоток, а перпендикулярно к ним (рис. 3.34, а). Нередко управляемый реактор изображают на схеме еще проще, опуская магнитопровод и вычерчивая обмотку подмагничивания в виде прямой линии, перпендикулярной к оси рабочей обмотки (рис. 3.34, б).

Рис. 3.33. Схема двух катушек, связанных магнитно

Рис. 3.34. Графическое изображение управляемых реакторов	в
электрических схемах

Тесты для самопроверки

1. Какой магнитный поток называется потоком рассеяния?

а. Поток, у которого часть пути проходит вне сердечника по воздуху. б. Поток, у которого весь путь проходит вне сердечника по воздуху. в. Поток, у которого весь путь проходит по сердечнику.

2. Укажите правильную формулу для определения потокосцепления.

а. S

w S .

б. S w S .

в. S S w.

3.С какой целью используют в дросселе сердечник, изготовленный из ферромагнитных сталей?

а. Из конструктивных соображений. б. Для увеличения магнитного потока.

в. Для увеличения магнитного сопротивления.

г. Для уменьшения потерь мощности в сердечнике.

4.Уравнение, описывающее электромагнитные процессы в дросселе имеет вид

u Ri ddt . Укажите, какой процесс отражает сопротивление R?

а. Потери мощности в активном сопротивлении обмотки. б. Потери мощности в ферромагнитном сердечнике.

в. Потери мощности в активном сопротивлении обмотки и ферромагнитном сердечнике.

5.Что является причиной нелинейных свойств дросселя? а. Ферромагнитный сердечник.

б. Активное сопротивление обмотки.

в. Сопротивление индуктивности рассеяния.

6.Какой вектор на векторной диаграмме указывает

на падение напряжения на сопротивлении обмотки?	4

								3
1	2	3	4	5	5					1
									2
а.	б.	в.	г.	д.							Ф

7. Какой вектор на векторной диаграмме указывает

на падение напряжения на сопротивлении										4
индуктивности рассеяния обмотки?
								3
				5							1
									2
1	2	3	4	5								Ф
а.	б.	в.	г.	д

8. Какой вектор на векторной диаграмме указывает

реактивную составляющую тока дросселя?	4

1	2	3	4	5			3
								2
а.	б.	в.	г.	д

9.Какой элемент на схеме замещения дросселя отражает потери мощности в сердечнике?

						R		LS
R	LS	b0	g0
а.	б.	в.	г.					b0

10.Какой элемент на схеме замещения дросселя обусловлен наличием потока рассеяния?

					R	LS
R	LS	b0	g0
а.	б.	в.	г.			b0

1

Ф

5

g0

g0

ГЛАВА 4. ЦЕПИ С ФЕРРОМАГНИТНЫМИ ЭЛЕМЕНТАМИ 4.1. Феррорезонансные цепи

Понятие о феррорезонансных цепях. Феррорезонансными цепями назы-

вают такие резонансные цепи, в которых в качестве индуктивных катушек используются ферромагнитные катушки. Вследствие нелинейности этих катушек, характер резонансных явлений в феррорезонансных цепях отличается рядом особенностей. В частности, условие резонанса в таких цепях при заранее заданных элементах может быть достигнуто не только подбором частоты, но и соответствующим изменением режима цепи по напряжению или току в ней.

Ниже рассмотрены два простейших примера феррорезонансных цепей, содержащих всего два элемента — ферромагнитную катушку и конденсатор. В

первом случае речь идет о последовательном соединении этих элементов, при котором наступает явление феррорезонанса напряжений, а во втором случае разобрано явление феррорезонанса токов, возникающее при параллельном соединении катушки и конденсатора.

Анализ цепей в обоих случаях проводится приближенным графическим методом, предложенным П. Л. Калантаровым в предположении, что потери энергии в катушке и конденсаторе отсутствуют, то есть они являются идеальными реактивными элементами. Кроме того, в целях упрощения не принимаются во внимание искажения кривых напряжений и токов, всегда имеющие место в таких цепях вследствие присутствия в них ферромагнитной катушки.

	а)				б)	I
				I

UL UC

Рис. 4.1. Цепь с последовательным соединением элементов L и C Феррорезонанс напряжений. Условие, при котором резонанс возникает в

цепи с последовательным соединением ферромагнитной катушки и конденсатора (рис. 4.1, а), нетрудно установить, если совместить на одном графике вольт-амперные характеристики этих элементов, снятые при той же частоте, при которой рассматривается работа цепи в целом. Напоминаем, что вольтамперная характеристика U L f I ферромагнитной катушки (рис. 4.2) по

форме аналогична кривой намагничивания ферромагнитного материала, а вольт-амперная характеристика UC f I конденсатора, являющегося линейным элементом, представляет собой прямую линию. Очевидно, что точка P пересечения этих характеристик и определяет собой режим, в частности ток I0 , при котором в цепи наступает резонанс. Действительно, при этом токе напряжения U L на катушке и U C на конденсаторе становятся равными друг другу,

что, как известно, является одним из критериев резонанса в простейшей последовательной цепи.

Таким образом, резонанс в последовательной феррорезонансной цепи с заданными ее элементами, в отличие от резонанса в аналогичной линейной цепи, может быть достигнут при заранее оговоренной частоте простым изменением тока или, что то же самое, изменением питающего цепь напряжения. Наоборот, цепь, настроенная в резонанс при определенной частоте, может быть легко выведена из него простым изменением тока или напряжения. Поэтому для этих цепей не существует понятия резонансной частоты. Впрочем и понятие резонансного тока I0 для этих цепей также условно, так как значение его меняется с

изменением частоты.

Заметим, что при токах в цепи, меньше резонансного значения I0 она имеет индуктивный характер, так как напряжение U L на катушке преобладает в этой области над напряжением UC конденсатора. Наоборот, при токах больших, чем I0 , цепь приобретает емкостный характер, поскольку в этой области

режимов U C U L .

Следует иметь в виду также, что достижение резонанса в рассматриваемой цепи только изменением тока или напряжения возможно не всегда. При достаточно малой емкости конденсатора, когда при заданной частоте его характеристика проходит круче начальной характеристики катушки (штриховая линия на рис. 4.2) и эти характеристики не пересекаются, равенство напряжений U L и U C не может наступить ни при каком токе в цепи.

I

I0

Рис. 4.2. Вольт-амперные характеристики элементов L и C

Вольт-амперная характеристика последовательной феррорезонанс-

ной цепи. Для более полного знакомства со спецификой режимов феррорезонансной цепи полезно обратиться к ее вольт-амперной характеристике, которая может быть построена по характеристикам входящих в нее катушки и конденсатора (рис. 4.2).

Из векторной диаграммы для рассматриваемой цепи (см. рис. 4.1, б), в которой при оговоренных ранее упрощениях напряжение U L на катушке опере-

жает ток I на 90°, а напряжение U C на конденсаторе отстает от тока на тот же

угол, следует, что напряжение питания U, определяющееся геометрической суммой

U U L U C ,

можно представить разностью действующих значений напряжений U L и U C :

U U L UC ,

поскольку векторы U L и U C оказываются развернутыми в противоположные стороны.

Поэтому для построения вольт-амперной характеристики U f I фер-

рорезонансной цепи в целом необходимо характеристику конденсатора С вычесть из характеристики катушки L в направлении оси напряжений, что и проделано на рис. 4.3, а. Формально при токах, больших резонансного значения I0 ,

полученная кривая должна опуститься ниже оси абсцисс (штриховая линия на рис. 4.3, а), поскольку разность U L UC приобретает в этой области отрицательный знак. Но, так как речь идет об оценке действующего значения напряжения цепи, отрицательную часть вольт-амперной характеристики U f I

обычно зеркально отражают в оси тока в область положительных значений напряжений (сплошная линия на рис. 4.3, а).

Особое внимание в полученной характеристике привлекает к себе точка ее соприкосновения с осью абсцисс, свидетельствующая, что при резонансе напряжение на зажимах всей цепи падает до нуля, несмотря на конечное значение тока I0 . Естественно, что этот результат явился следствием пренебрежения ак-

тивным сопротивлением цепи и, следовательно, активной составляющей напряжения, не компенсирующейся при резонансе. Поэтому в реальных условиях вольт-амперная характеристика в точке резонанса не опускается до самой оси, однако характерный падающий участок a в кривой до ее минимума в области резонансного значения тока I0 сохраняется (сплошная кривая на рис. 4.3, б).

При этом, чем дальше отстоит режим цепи от резонанса, тем меньше расхождения между теоретической и практической вольт-амперными характеристиками цепи.

Одной из специфических особенностей феррорезонансных цепей является многозначность их вольт-амперной характеристики по отношению к напряжению. Иначе говоря, в некоторой области напряжений, например между значениями U B и Ua на рис. 4.3, и. одному заданному значению напряжения соот-

ветствуют три различных значения I1 , I 2 , I3 тока.

Следует иметь в виду и некоторую неопределенность положения вольтамперной характеристики ферромагнитной цепи, свойственную всем нелинейным элементам и соответственно цепям, содержащим эти элементы. Так, при питании цепи синусоидальным напряжением минимум практической кривой опускается заметно ниже (кривая 1 на рис. 4.3, в), чем в случае питания цепи синусоидальным током (кривая 2). Это объясняется тем, что в последнем случае напряжение на катушке искажено, то есть в его кривой содержатся высшие гармоники. Напряжение же конденсатора при синусоидальном токе синусоидально, и поэтому оно компенсирует при резонансе только первую гармонику напряжения катушки. В результате к активному напряжению цепи в этом режиме добавляются нескомпенсированные высшие гармоники напряжения катушки, поднимая уровень минимального действующего напряжения при резонансе.

Об устойчивости режимов в последовательной феррорезонансной це-

пи. Вольт-амперная характеристика последовательной феррорезонансной цепи в том виде, как она показана на рис. 4.3, б, может быть полностью снята опытным путем лишь при условии питания цепи заданным по величине током. Тогда по мере увеличения этого тока напряжение цепи будет сначала увеличиваться от нуля до значения U a , а затем падать до величины U B с тем, чтобы за точкой ре-

зонанса вновь начать увеличиваться при дальнейшем возрастании тока.

Если же вольт-амперную характеристику этой цепи снимать, питая цепь заданным по величине напряжением, то установить режимы, соответствующие падающему участку a в характеристики (рис. 4.3, б), не удается, так как они оказываются неустойчивыми. При этом по мере увеличения напряжения от нуля ток в цепи будет плавно возрастать до значения I a , соответствующего точке

а в максимуме характеристики (рис. 4.3, г). Попытка дальнейшего увеличения напряжения приводит к быстрому лавинообразному процессу изменения режи-

ма, при котором ток практически скачкообразно возрастает от значения I a до значения Iб . Лишь после этого дальнейшее увеличение напряжения вновь вле-

чет за собой плавное увеличение тока в соответствии с возрастающим участком характеристики за точкой б. При последующем уменьшении напряжения режим цепи изменяется плавно до точки в, после чего вновь наступает лавинообразный процесс, сопровождающийся скачкообразным уменьшением тока от значения Iв до значения I г .

а)

б)

в)

г)

Рис. 4.3. Построение вольт-амперной характеристики U f I феррорезонансной цепи

Обратим внимание, что точка a лежит в области, где цепь имеет индуктивный характер, то есть ток отстает от напряжения, а точка б относится к области, где характер цепи емкостный, то есть опережает напряжение. Поэтому рассмотренный выше скачкообразный переход режима от точки a в точку б при увеличении питающего напряжения сопровождается к тому же явлением опрокидывания фазы, то есть скачкообразным изменением разности фаз напряжения и тока почти на 180 0 . Резкое изменение фазового угла цепи происходит и при обратном скачке режима из точки в в точку г (рис. 4.3, г).

Феррорезонанс токов. Условие резонанса в цепи при параллельном соединении ферромагнитной катушки и конденсатора (рис. 4.4, а) также определяется точкой p пересечения их вольт-амперных характеристик (рис. 4.5).

Только в этом случае их удобнее рассматривать как зависимости токов I L катушки и IC конденсатора от напряжения U . Соответственно этому в точке p теперь следует обратить внимание на равенство I L IC упомянутых токов, свидетельствующее о резонансе в простейшей параллельной цепи, и говорить о ее резонансном напряжении U 0 (при заданной частоте питания).

IC		IL

Рис. 4.4. Резонанс в цепи при параллельном соединении ферромагнитной катушки и конденсатора

При напряжениях ниже резонансного значения U 0 цепь будет иметь емкостный характер, так как в этой области IC I L , а при напряжениях U U 0 цепь приобретает индуктивный характер I L IC .

Как и в последовательной цепи, феррорезонанс возможен только при относительно больших емкостях конденсатора, когда его характеристика распо-

лагается положе начального участка характеристики катушки, то есть когда имеет место пересечение этих характеристик.

Вольт-амперная характеристика параллельной феррорезонансной цепи может быть построена, принимая во внимание, что ток I L в идеальной катушке

отстает от напряжения на 90° (рис. 4.4, б), а ток IC конденсатора опережает это напряжение на 90°.

Р

U0

Рис. 4.5. Вольт-амперная характеристика цепи при параллельном соединении ферромагнитной катушки и конденсатора

Поэтому ток I в неразветвленной части цепи может быть определен не геометрической суммой векторов:

IIC I L ,

аарифметической разностью действующих значений токов конденсатора и ка-

тушки:

I IC I L

Это значит, что построение вольт-амперной характеристики цепи сведется к вычитанию характеристики катушки из характеристики конденсатора в направлении оси токов (рис. 4.6, а).

Отказавшись от формального понятия отрицательного действующего тока I в области напряжений выше точки резонанса, зеркально отобразим верхний участок результирующей характеристики в оси ординат, то есть предста-

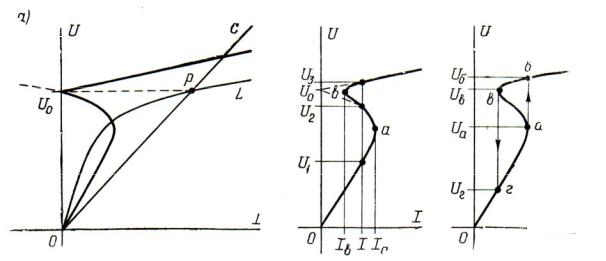
вим характеристику цепи в том виде, как она показана на рис. 4.6, а, сплошной линией.

Таким образом, ток I всей цепи в целом при резонансном напряжении U0 теоретически обращается в нуль. В действительности из-за наличия актив-

ной проводимости катушки этого, конечно, быть не может, и практически вольт-амперная кривая в области резонанса лишь приближается к оси ординат, как показано на рис. 4.6, б сплошной линией.

а)	б)	в)

	I
Рис. 4.6. Вольт-амперная характеристика параллельной	ферро-
резонансной цепи

На этот раз приходится говорить о многозначности вольт-амперной характеристики цепи относительно тока в области его значений от I В до I a , где

одному значению тока I соответствуют три различных значения U1 ,U 2 ,U3 на-

пряжения.

Аналогично случаю последовательной феррорезонансной цепи здесь мы также сталкиваемся с некоторой неопределенностью расположения вольтамперной характеристики, связанной с различными проявлениями высших гармоник напряжения и тока. В частности, минимум тока в области резонанса проявляется при синусоидальном токе в цепи значительно ярче, чем при синусоидальном напряжении на ней.

Неустойчивые режимы в параллельной феррорезонанcной цепи связаны с падающим участком a в вольт-амперной характеристики и наблюдаются в этой цепи при питании ее от источника с заданным действующим значением тока. Например, при увеличении тока I от нуля напряжение цепи вначале возрастает плавно до значения U a (рис. 4.6, б), соответствующего точке а на ее

характеристике. При ничтожном дальнейшем возрастании тока возникает ска-

чок напряжения от значения U a до значения Uб , после чего вновь наступает

устойчивость режимов в цепи, и дальнейшему увеличению тока соответствует монотонное увеличение напряжения. При уменьшении тока устойчивость режимов наблюдается до точки в характеристики, из которой происходит новый срыв режима в точку г, сопровождающийся скачкообразным спадом напряжения от значения U В до значения U 2 . Таким образом, при питании цепи задан-

ным током I режимы, соответствующие падающему участку a в характеристики, получены быть не могут.

На этом участке устойчивые режимы возможны только при условии питания цепи заданным напряжением U. Именно таким образом практически удается снять всю вольт-амперную характеристику цепи, представленную на рис. 4.6, б.

Как и при скачках тока в последовательной феррорезонансной цепи, скачки напряжения в параллельной феррорезонансной цепи сопровождаются явлением опрокидывания фазы. В частности, при срыве режима цепи из точки а в точку б (рис. 4.6, в) наблюдается скачкообразное изменение фазового угла от значения, близкого к 900 , к значению, почти равному 900 , так как в области ниже резонансного напряжения U 0 цепь имеет емкостный характер, а в области выше U 0 - индуктивный.

4.2. Ферромагнитные стабилизаторы напряжения

Принцип действия ферромагнитных стабилизаторов переменного напряжения не отличается от принципа действия рассмотренного ранее газоразрядного стабилизатора постоянного напряжения. В обоих случаях прибегают к последовательному соединению линейного и нелинейного элементов электрической цепи, причем второй из них должен иметь достаточно пологий участок вольт-амперной характеристики. Тогда колебания напряжения на всей цепи в основном принимает на себя линейный элемент, а напряжение на нелинейном элементе остается почти неизменным.

Следует подчеркнуть, что в цепях переменного тока эта задача получает более удачное решение с энергетической точки зрения, так как возможность использования здесь реактивных элементов цепи существенно снижает потери энергии в процессе стабилизации. Ниже приведены описания нескольких схем ферромагнитных стабилизаторов и анализ их работы, причем во всех случаях в целях упрощения элементы цепей стабилизаторов, в частности, ферромагнит-

ной катушки принимаются идеальными, то есть без потерь. Кроме того, рассматриваются лишь простейшие режимы стабилизаторов при отсоединенной нагрузке (режимы холостого хода).

Простейшая схема стабилизатора содержит две последовательно соединенные индуктивные катушки L1 и L2 (рис. 4.7), первая из которых имеет ли-

нейную вольт-амперную характеристику 1, а вторая - типичную нелинейную характеристику 2 ферромагнитной катушки

(рис. 4.8). Входное, подлежащее стабилизации напряжение U1 подается на всю цепь в целом (рис. 4.7), а выходное стабилизированное напряжение U 2 снимается с нелинейной катушки L2 .

Рис. 4.7. Простейшая схема стабилизатора

При оговоренных в предыдущем пункте упрощениях действующее значение входного напряжения U1 определяется арифметической суммой дейст-

вующих напряжений U L1 и U 2 на последовательно соединенных катушках:

U1 U L1 U 2 ,

и вольт-амперная характеристика 3 всей цепи может быть получена путем сложения характеристик обеих катушек в направлении оси напряжений (рис. 4.8).

Рис. 4.8. Вольт-амперные характеристики катушек с L1 и L2

Пусть первоначально входное напряжение имело некоторое значение U1 . Соответствующее значение тока I в цепи найдем по характеристике 3 (операция а—б), а выходное напряжение U 2 при этом токе определим по характеристике 2 катушки L2 (опeрация e г). Предположим теперь, что входное напряжение возросло до значения U1 , которому будут соответствовать новые значения тока I в цепи и выходного напряжения U 2 . Выполненные построения по-

казывают, что изменение U 2 U 2	U 2 выходного напряжения значительно
меньше происшедшего изменения	U1 U1 U1 входного напряжения, что
свидетельствует об эффекте стабилизации напряжения.
Очевидно, что коэффициент стабилизации напряжения
kC		U1	:	U 2	,
		U1		U 2

определяющийся отношением соответствующих друг другу относительных изменений входного и выходного напряжений, будет тем выше, чем более пологой окажется характеристика ферромагнитной катушки в области насыщения. В этом отношении желательно режим работы стабилизатора выбирать в области достаточно больших токов, обеспечивающих сильное насыщение магнитопровода нелинейной катушки L2 . Однако это связано с излишней нагрузкой источ-

ника питания стабилизатора, и поэтому с энергетической точки зрения такие стабилизаторы оказываются нерентабельными.

Следует иметь в виду также, что нагрузка стабилизатора, присоединенная параллельно его нелинейному элементу, в какой-то мере неизбежно влечет за собой приближение вольт-амперной характеристики этой части цепи к линейной и, таким образом, ведет к ухудшению процесса стабилизации. Опыт показывает, что для удовлетворительной работы стабилизатора реактивная мощность его элементов должна в несколько раз превосходить мощность нагрузки.

Феррорезонансный стабилизатор. С целью уменьшения тока во вход-

ной цепи стабилизатора в качестве его нелинейного элемента целесообразно применить параллельную феррорезонансную цепь (см. рис. 4.4, а), пологий участок вольт-амперной характеристики которой (см. рис. 4.6, б) начинается близко от оси ординат, то есть при относительно малых токах. В качестве линейного элемента в этих стабилизаторах обычно используют также ферромагнитную катушку, в магнитопроводе которой для создания линейности ее вольтамперной характеристики предусматривается воздушный зазор. Схема такого стабилизатора показана на рис. 4.9, а его работа иллюстрируется построениями на рис. 4.10, где, правда, используется другой прием графического анализа последовательного соединения двух элементов цепи, не требующий построения результирующей характеристики цепи. При этом методе в обычной системе координат строится характеристика только одного элемента Цепи, в данном случае кривая 2 феррорезонансного контура. Характеристика другого элемента (на рис. 4.10 это характеристика 1 линейной катушки L1 ) вычерчивается опрокину-

той вокруг оси абсцисс. К тому же ось токов этой характеристики переносится параллельно самой себе вверх на величину питающего цепь напряжения U1 .

Например, при небольшом напряжении U1 ось I , а вместе с ней и характеристика 1 располагаются ниже, а при повышенном напряжении U1 они подни-

маются вверх. Точки a и a пересечения характеристик 2 и 1 определяют собой токи I и I стабилизатора в двух рассматриваемых режимах и соответствующие выходные напряжения U2 и U2 .

Заметим, что стабилизация выходного напряжения при понижении входного напряжения имеет место в этой схеме только до определенного предела. Если входное напряжение падает ниже значения, при котором точка а достигает минимума характеристики I f U феррорезонансной цепи, то процесс ста-

билизации полностью нарушается или, как принято говорить, наступает срыв стабилизации.

Рис. 4.9. Схема феррорезонансного стабилизатора

Рис. 4.10. Вольт-амперная характеристика феррорезонансного стабилизатора

4.3. Ферромагнитные умножители частоты

Умножители частоты представляют собой статические, то есть не имеющие подвижных частей устройства, с помощью которых можно от источника электрической энергии с частотой f получить переменный ток с частотой

kf , в k раз превышающей частоту источника. Среди мощных умножителей час-

тоты наибольшее распространение получили ферромагнитные умножители, основными элементами которых являются ферромагнитные катушки. Принцип

действия этих умножителей основан на искажении форм кривых тока и напряжения ферромагнитными катушками с последующим выделением высшей гармоники определенной кратности.

Резонансный ферромагнитный умножитель частоты, схема которого представлена на рис. 4.11, является простейшим по принципу действия этого рода умножителей. Ферромагнитная катушка L включена во входной контур умножителя последовательно с резонансным контуром, состоящим из линейной катушки L1 и конденсатора C1. С помощью этого контура, настроенного в ре-

зонанс при частоте питания f и поэтому играющего роль прозрачного фильтра,

этой частоте удается приблизить форму кривой тока ферромагнитной катушки к синусоидальной. При этом достигается значительное искажение формы кривой напряжения на нелинейной катушке L и появление в его кривой ряда нечетных высших гармоник. Приемник П присоединен к катушке через прозрачный фильтр Ф, настроенный на одну из этих гармоник. Поэтому в кривой напряжения приемника она будет преобладать над всеми остальными гармониками, играя роль па выходе умножителя основной гармоники с частотой, в целое число раз превосходящей частоту входного напряжения. Форма кривой выходного напряжения зависит от качества второго фильтра и при желании может быть получена достаточно синусоидальной.

Рис. 4.11. Схема резонансного ферромагнитного умножителя частоты

При помощи таких умножителей удается достичь умножения частоты в несколько десятков раз.

Ферромагнитный утроитель частоты состоит из трех одинаковых трансформаторов с ферромагнитным магнитопроводом, первичные обмотки w1

которых соединены звездой, а вторичные w2 — последовательно друг с другом (рис. 4.12). Питание первичных обмоток осуществляется от трехфазной сети с частотой f , а напряжение утроенной частоты 3 f снимается с крайних выводов цепи вторичных обмоток.

f
		3f

Рис. 4.12. Схема ферромагнитного утроителя частоты

Работу утроителя рассмотрим в простейшем режиме холостого хода, то есть при отключенной нагрузке, полагая, что питающие напряжения синусоидальны и составляют симметричную систему. Нетрудно убедиться, что магнитный поток в каждом из трансформаторов в этом случае не может быть синусоидальным. Действительно, при синусоидальном потоке ток в первичных обмотках был бы несинусоидален и содержал среди прочих гармоник и гармоники, кратные трем. Однако, последнее невозможно, так как при соединении звездой без нейтрального провода токи третьей и кратных ей гармоник существовать не могут. Следовательно, магнитные потоки трансформаторов будут несинусоидальными. Более того, кривые потоков и индуктируемых ими ЭДС могут содержать только третью и кратные ей гармоники. В самом деле, линейные напряжения, питающие утроитель, по условию синусоидальны. Но так как линейные напряжения равны разностям фазных ЭДС, индуктируемых в первичных обмотках трансформаторов, то эти ЭДС могут иметь лишь те гармоники, порядок которых кратен трем. Ведь только эти гармоники совпадают по фазе и при

вычитании могут взаимно скомпенсироваться, что обязательно необходимо при условии синусоидальности линейных напряжений. Таким образом, индуктируемые во вторичных обмотках трансформатора ЭДС будут, кроме основной грмоники, содержать лишь третью и кратные ей гармоники. Основные гармоники ЭДС вторичных обмоток, сдвинутые в различных трансформаторах по фазе на треть периода, суммируясь, дадут в выходной цепи утроителя нуль, а все высшие гармоники одного порядка, наоборот, совпадающие по фазе, при сложении в этой цепи по величине утроятся. В результате роль основной гармоники в выходном напряжении утроителя будет играть третья гармоника, частота которой в три раза превосходит частоту питающей сети.

Ферромагнитный удвоитель частоты состоит из двух одинаковых фер-

ромагнитных катушек с подмагничиванием, рабочие обмотки w1 которых, соединенные последовательно, образуют входную цепь удвоителя, питаемую переменным напряжением с частотой f (рис. 4.13). Выходную цепь удвоителя, на зажимах которой, как будет показано ниже, действует напряжение удвоенной частоты 2 f , составляют дополнительные обмотки w2 , также соединенные друг с другом последовательно аналогично обмоткам wП подмагничивания.

Переходя к объяснению принципа действия ферромагнитного удвоителя частоты, обратим внимание, что его рабочие обмотки w1 соединены друг с дру-

гом наоборот по сравнению с обмотками wП подмагничивания (конец одной обмотки подмагничивания соединен с началом другой, а обе

рабочие обмотки соединены своими концами). Поэтому МДС F рабочих обмоток в разных магнитопроводах в каждый данный момент будут действовать по отношению к МДС FП обмоток подмагничивания в противоположные сто-

роны. Если последние в обоих магнитопроводах принять положительными, то положительному значению рабочей МДС в одном магнитопроводе будет соответствовать такое же по величине, но отрицательное значение МДС в другом магнитопроводе. Иными словами, переменные МДС рабочих обмоток, а вместе с ними и переменные составляющие магнитных потоков двух магнитопроводов следует считать сдвинутыми по фазе на полпериода (180°).

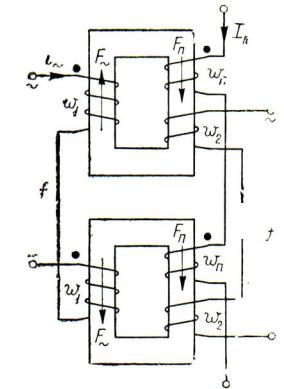
i

f

2f

Рис. 4.13. Схема ферромагнитного удвоителя частоты

Вспомним теперь, что при подмагничивании ферромагнитного магнитопровода постоянным током искажение форм кривых магнитных потоков сопровождается появлением в них четных гармоник. Примем также во внимание, что для всех четных гармоник (второй, четвертой и т. д.) сдвиг всей кривой на полпериода соответствует сдвигу на целое число их периодов (для второй на один, для четвертой на два и т. д.). Фактически это означает, что все четные гармоники потоков будут совпадать в двух магнитопроводах по фазе. Соответственно будут совпадать по фазе и индуктированные ими в дополнительных обмотках w2 четные гармоники ЭДС. А поскольку эти обмотки соединены по отноше-

нию к положительным направлениям потоков согласно (см. рис. 4.13), то в выходной цепи удвоителя четные гармоники ЭДС будут складываться, давая на выходе удвоителя удвоенное значение напряжения четных гармоник по сравнению с ЭДС каждой обмотки. ЭДС же первой гармоники, индуктированные в этих обмотках и сдвинутые по фазе на полпериода, наоборот, полностью скомпенсируют себя в выходной цепи, в результате чего роль основной волны в выходном напряжении будет играть вторая гармоника, частота которой в два раза выше частоты питающего напряжения.

4.4. Ферромагнитные усилители

Простейший ферромагнитный усилитель, обычно называемый сокращенно магнитным усилителем, представляет собой управляемый реактор L, включенный последовательно с нагрузкой z, питающийся от источника переменного тока с неизменным действующим значением напряжения U И (рис. 4.14, а).

а)	б)	I

z

I0

IУ

в)

I

		IУ	I0	IУ
Рис. 4.14. Схема простейшего ферромагнитного усилителя
При изменении постоянного тока IY				подмагничивания, называемого в

данном случае током управления, изменится индуктивность управляемого реактора, что, в свою очередь, вызовет изменения тока I , напряжения U и полной мощности S = UI нагрузки. При этом между током I в нагрузке и током управления IY будет существовать определенная функциональная зависимость, на-

зываемая характеристикой управления (рис. 4.14, б). Отличительной особенностью этой характеристики, имеющей сравнительно большой линейный участок, является начальный ток I0 нагрузки. К сожалению, устранить этот ток, то есть

добиться, чтобы характеристика выходила из начала координат при этой схеме усилителя не представляется возможным: при отсутствии тока управления управляемый реактор все же обладает некоторой остановочной проводимостью, которая и определяет этот ток.

Таким образом, в рассматриваемой цепи представляется возможность управлять режимом работы нагрузки переменного тока с помощью постоянного

тока. Усилителями же эти устройства называются потому, что соответствующим подбором конструктивных параметров реактора, и в первую очередь, чисел витков рабочей обмотки и обмотки управления удается достичь режимов, при которых управляемый ток I , напряжение U или полная мощность S нагрузки окажутся больше соответственно тока управления IY , приложенного к

цепи подмагничивания напряжения управления UY или мощности управления PY UY IY , расходуемой в цепи управления. В первом случае говорят об усилителе тока, оценивая его коэффициентом усиления тока

kI IIY ,

во втором случае усилитель называют усилителем напряжения, интересуясь его коэффициентом усиления напряжения

kU U , UY

а в последнем, наиболее широко распространенном случае рассматривают усилитель как усилитель мощности, определяя его коэффициент усиления мощности выражением

kP S . PY

Из принципа действия управляемого реактора вытекает, что рассмотренный усилитель не будет реагировать на изменение направления тока управления. Поэтому его характеристика в области отрицательных токов управления представляет собой зеркальное отображение в оси ординат характеристики в первом квадранте (рис. 4.14, в).

Начальное подмагничивание. Если необходимо, чтобы усилитель реагировал на знак тока управления, то есть на изменение его направления, прибегают к начальному подмагничиванию управляемого реактора, достигаемого с помощью дополнительной обмотки начального подмагничивания. Пропуская по этой обмотке постоянный ток начального подмагничивания I П (рис. 4.15, а),

выводят режим работы магнитного усилителя на середину прямолинейного участка его характеристики (рис. 4.15, б). Если теперь по обмотке управления пропустить ток IY , согласный по направлению с током подмагничивания, то

результирующее подмагничивание реактора увеличится и ток I нагрузки возрастет. При противоположном направлении тока управления результирующее подмагничивание уменьшится и ток нагрузки упадет. Естественно, что при от-

сутствии тока управления ток нагрузки будет иметь увеличенное начальное значение I0 .

а)	б)

Рис. 4.15. Ферромагнитный усилитель с начальным подмагничиванием

Дифференциальный ферромагнитный усилитель. С целью смещения характеристики управления усилителя так, чтобы она выходила из начала координат, то есть чтобы при отсутствии тока управления ток нагрузки также равнялся нулю, прибегают к дифференциальным ферромагнитным усилителям. В этих усилителях имеются два одинаковых управляемых реактора L1 и L2 с на-

чальным подмагничиванием, включенных совместно с нагрузкой z по схеме, представленной на рис. 4.16, а. Питание цепи осуществляется двумя равными по величине и фазе напряжениями U H1 и U H 2 двух секций вторичной обмотки

трансформатора Т. В этом случае ток I нагрузки равен разности рабочих токов I1 и I2 двух реакторов:

I I1 I2 .

Поэтому при одинаковом подмагничивании обоих управляемых реакторов, достигаемом только током I П начального подмагничивания при отсутст-

вии тока IY управления, когда рабочие токи I1 и I2 равны друг другу, ток нагрузки I обращается в ноль. При появлении же тока IY в обмотках управления, соединенных друг с другом так, что в одном реакторе он усиливает начальное подмагничивание, а в другом — ослабляет (см. рис. 4.16, а), равенство токов I1 и I2 нарушается и в нагрузке начинает протекать ток I . Если начальным подмагничиванием реакторы были выведены примерно на середину их характери-

стики управления (см. рис. 4.16, б), то зависимость I f IY выходного тока от

тока управления на значительном участке приобретает практически линейный характер (рис. 4.16, б). При этом изменение направления тока управления вызывает изменение фазы выходного тока на 180°. Последнее иногда отражают, вычерчивая ветвь характеристики управления в области отрицательных токов управления в третьем квадранте (штриховая линия на рис. 4.16, б).

а)

б)

Рис. 4.16. Схема дифференциального ферромагнитного усилителя

Тесты для самопроверки

1. Укажите элемент в схеме замещения дросселя, характеризующий магнитный поток, замыкающийся по сердечнику.

i	R		L s

а. b0

u

g0

b0

б. R в. g0 г. LS

2. Укажите вольт-амперную характеристику нелинейной индуктивности последовательной феррорезонансной цепи.

U

1

2

3

4

а. 2 б. 3 в. 4 г. 1

3. Укажите ВАХ активного сопротивления обмотки дросселя феррорезонансной цепи.

U	1
	2
а. 3	4
б. 1	3
в. 4
г. 2	I

4. Укажите характеристику последовательной феррорезонансной цепи.

	U	1
		2
	а. 3	3
	б. 1
		4
	в. 4
	г. 2
		I

5. На каком принципе основана работа ферромагнитного удвоителя частоты? а. При подмагничивании ферромагнитного магнитопровода постоянным

током искажение форм кривых магнитных потоков сопровождается появлением в них четных гармоник.

б. Несимметричная нагрузка вызывает токи обратной последовательно-

сти.

в. Искажение формы входного трехфазного напряжения.

6. Укажите для феррорезонансной цепи вольт-амперную характеристику емкости.

	U	1
		2
	а. 1
	б. 3	3
	в. 2
		4
	г. 4

I

7. На каком принципе основана работа магнитного усилителя?

а. При изменении постоянного тока IY подмагничивания изменяется ин-

дуктивность управляемого реактора вследствие его нелинейности.

б. Омическая нагрузка усилителя больше внутреннего сопротивления источника.

в. Омическая нагрузка усилителя меньше внутреннего сопротивления источника.

8. С какой целью применяют начальное подмагничивание в магнитном усилителе?

а. Чтобы усилитель не реагировал на знак тока управления.

б. Чтобы омическая нагрузка усилителя была больше внутреннего сопротивления источника.

в. Чтобы усилитель реагировал на знак тока управления.

ЧАСТЬ II. ТЕОРИЯ ПЕРЕХОДНЫХ ПРОЦЕССОВ В ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ

ГЛАВА 5. КЛАССИЧЕСКИЙ МЕТОД РАСЧЕТА ПРОЦЕССОВ В ЛИНЕЙНЫХ ЦЕПЯХ С СОСРЕДОТОЧЕННЫМИ ПАРАМЕТРАМИ

5.1.Основные понятия о переходных процессах

Впредшествующих разделах курса рассматривались установившиеся процессы в цепях с сосредоточенными параметрами. Напомним, что цепи с сосредоточенными параметрами – это такие цепи, для которых с достаточной степенью точности можно считать, что электрическое поле, магнитное поле и выделение тепла сосредоточены на отдельных участках цепи, т. е. параметрам

R, C, L отводится определенное отдельное место, при этом их геометрические размеры не учитываются.

Установившимся процессом, или режимом, называется такой процесс, который протекает в рассматриваемый момент времени при условии, что все изменения (включение или отключение источников, нагрузки; изменение параметров цепи и др.) происходили теоретически при t , практически при достаточно большом времени в прошлом.

Переходный процесс в электрической цепи - это переход от одного установившегося режима к другому, отличному от первого. Такие процессы имеют место при коммутации, т. е. при включении или отключении электрических цепей, при достаточно быстрых изменениях величины и формы напряжения и параметров цепи. Возникновение переходных процессов обусловлено свойством реактивных элементов индуктивности и емкости накапливать энергию электромагнитного поля и возвращать ее во внешнюю цепь в достаточно короткий промежуток времени.

На схеме обычно коммутация указывается в виде рубильника со стрел-

кой. На рис. 2.1,а	стрелка означает включение рубильника, стрелка на рис.
2.1,б – отключение.
а)	б)

Рис. 5.1. Коммутационные ключи Весь процесс в электрических цепях можно разделить на три режима:

1.Начальный установившийся режим, который имел место до мутации.

2.Переходный режим. Его начало обычно принимается в момент времени

t = 0.

3. Конечный установившийся режим после коммутации, который наступает теоретически при t , а практически, как будет показано ниже, через сравнительно короткое время.

Длительность переходного процесса исчисляется обычно весьма малыми долями секунды, но токи и напряжения за это время могут достигнуть значений значительно больших величин, чем в установившемся режиме, а это может привести к повреждению электрооборудования. Кроме того, в таких областях техники, как электроника, радиотехника, автоматика и др., важно знать о характере переходных процессов, что позволяет определить характеристики систем.

Следовательно, изучение и расчет переходных режимов являются актуальной задачей.

Прежде чем приступить к расчету переходных процессов, рассмотрим два важных вопроса: начальные условия и законы коммутации.

5.2. Законы коммутации. Начальные условия

Переходные процессы связаны с изменением магнитной энергии в индуктивности L и электрической энергии в емкости С и запасом этих энергий на момент коммутации.

Энергия магнитного поля в индуктивности

WМ		Li2		2			(5.1)
		L		2L
		2
и энергия электрического поля на емкости
W	СuC2				q2		(5.2)
Э		2			2C

не могут изменяться мгновенно, так как для мгновенного изменения энергии потребовались бы бесконечно большие мощности источников, что физически невозможно.

Если учесть, что индуктивность L и емкость С неизменны, то из соотношения (2.1) следует, что ток и потокосцепление в индуктивности не могут изменяться скачком (мгновенно). Это положение известно под названием первого закона коммутации. Из соотношения (2.2) следует, что напряжение на емкости и его заряд не могут изменяться скачком (мгновенно). Это положение на-

зывается вторым законом коммутации.

Для учета влияния энергетического состояния цепи на момент коммутации и для записи законов коммутации введем понятия тока iL ( 0) в индук-

тивности и напряжения uC ( 0) на емкости в последний момент перед коммутацией, а также понятия тока iL ( 0) в индуктивности и напряжения uC ( 0) на емкости в первый момент после коммутации. Напомним, что за момент комму-

тации принято время t = 0. В соответствии с этим законы коммутации можно записать в виде:

первый закон коммутации iL ( 0) iL ( 0)	или ( 0) ( 0);	(5.3)
второй закон коммутации uC ( 0) uC ( 0)	или q( 0) q( 0) .	(5.4)

Заметим, что напряжение на индуктивности и ток в емкости могут изменяться мгновенно.

Если цепь содержит только активные сопротивления, то запасенная энергия электрического и магнитного полей несоизмеримо мала с выделяющейся тепловой энергией в сопротивлениях, что обусловливает отсутствие переходных процессов в таких цепях. При этом ток и напряжения изменяются мгновенно от первоначально установившегося режима до нового установившегося режима. Независимыми начальными условиями называются токи iL(-0) в индуктивностях и напряжения uC(-0) на емкостях. В дальнейшем для краткости будем их называть начальными условиями. Если iL(-0)=0 и uC(-0)=0, то такие начальные условия называются нулевыми.

В отдельных случаях могут быть использованы зависимые начальные условия - значения токов и напряжений на других участках цепи при t(+0), например на резистивных элементах. Следует отметить, что характер переходного процесса зависит от начальных условий.

5.3. Основы классического метода

Электромагнитные процессы в электрических цепях описываются дифференциальными уравнениями, составленными согласно первому и второму законам Кирхгофа. Порядок дифференциального уравнения определяется тем, сколько в цепи имеется накопителей электрической и магнитной энергии. Если требуется найти ток ik в k -й ветви, то исключая последовательно все токи остальных ветвей, можно получить одно дифференциальное уравнение, содержащее только ток ik и его производные:

a

d nik

a

d n 1ik

...a

dik

a

i

f (t).

(5.5)

n dt n

n 1 dt n 1

k

1 dt

0

Здесь

an , an 1 , a1 , a0 -

постоянные коэффициенты, значения которых

зависят от конфигурации цепи. Правая часть f(t) содержит в себе заданные ЭДС.

Полный интеграл дифференциального уравнения с правой частью равен сумме частного решения этого уравнения и решения того же уравнения без правой части (однородного) 1 .

Частное решение уравнения (5.5) дает нам значение тока при t = , т. е. при установившемся режиме, наступившем после коммутации. Характер и величина этой составляющей определяются внешними источниками. Поэтому ее часто называют принужденной составляющей и обозначают как iпр. Например, если источники постоянны, то и принужденный ток iпр = const. Если же ЭДС заданы в виде синусоидальных функций, то iпр также будет синусоидальной функцией. Определение iпр является задачей расчета установившегося режима в цепи, способы и методы которого рассматривались в предыдущих разделах курса ТОЭ -1.

Общее решение физически определяет электромагнитные процессы, происходящие в цепи при отсутствии внешних источников энергии, за счет запаса энергии в индуктивностях и емкостях, который был в начальный момент времени.

Так как в реальных цепях всегда имеет место рассеяние энергии (преобразование в тепло), то запас энергии будет со временем исчерпан и электромагнитные процессы в цепи прекратятся.

Из этого следует, что общее решение однородного уравнения должно стремиться к нулю при t . Эта составляющая не зависит от внешних источников, и поэтому ее часто называют свободной составляющей и обозначают как

iсв.

Общее решение однородного дифференциального уравнения n-го порядка, как известно из курса математики в случае простых корней, имеет вид

iсв =	n
	A е kt		,
	k 1	k

где t – время; Ak – постоянные интегрирования, определяемые из начальных условий; – корни характеристического уравнения

an n + a n-1 n-1 + … + a 1 + a0 = 0.

(5.6)

Для получения характеристического уравнения (5.6) необходимо в однородном дифференциальном уравнении заменить i на 1, первую производную тока didt на , вторую производную на 2 и т. д.

Следует отметить, что корни характеристического уравнения могут быть отрицательными числами и комплексными с отрицательной вещественной частью. При этих условиях экспоненциальные функции стремятся к нулю при

t , т. е. iсв 0. Это также согласуется с физической сущностью переходных процессов, которые при t стремятся к установившемуся режиму, т.

е. i iпр.

Рассмотренный метод расчета переходных процессов называется классическим. Обратим внимание, что при составлении дифференциальных уравнений в качестве неизвестных необходимо принимать ток iL в индуктивности и напряжение uC на емкости. При таком выборе неизвестных достаточно легко на основании начальных условий и законов коммутации определить постоянные интегрирования.

Расчет переходных процессов целесообразно вести в следующей последовательности.

1.В заданной электрической схеме до коммутации (t - 0) определяем

начальные условия, т.е. токи iL (-0) в индуктивностях и напряжения uC (-0) на емкостях. При этом для их нахождения используем методы расчета установившегося режима, известные нам из предыдущих тем курса.

2.Изображаем электрическую цепь, образованную после коммутации (t 0), и, выбрав направления токов и напряжений в ветвях, составляем уравнения по законам Кирхгофа для мгновенных значений токов и напряжений.

3.Используя уравнения связи между мгновенными значениями тока и напряжения для элементов R, L, С

uR = RiR;	uL = L	diL	;	iC =C	duC	,	(5.7)
		dt			dt

исключаем из уравнений п.2 все неизвестные токи и напряжения кроме ik L или ukC . В результате получаем дифференциальное уравнение n-го порядка относительно тока ikL или напряжения ukC вида (5.5).

4.Представляем решение дифференциального уравнения, составленного

вп.3, в виде суммы принужденной и свободной составляющих:

ikL = ikL пр + ikL св или	ukC = ukC пр + ukC св .	(5.8)
5. Определяем принужденные составляющие ikLпр или ukCпр		, используя

при этом методы расчета установившегося режима.

6. Преобразуем исходное дифференциальное уравнение из п.3 в однородное дифференциальное уравнение приравниванием правой части исходного уравнения к нулю. При этом решением однородного уравнения будет являться искомая свободная составляющая

		n			t		n	S t
	ikLсв=	AkS		S		или	ukCсв= AkS e		.	(5.9)
		S 1					S 1

7. Определяем корни S характеристического уравнения , полученного из дифференциального однородного уравнения , путем замены ikLсв и ukCсв на 1, а

dikLn

dun

n

их производных

n – го порядка

св

,

kС

на

.

dt n

dtn

8. Записываем уравнение, например, для тока iL в виде (дальнейшие

пункты алгоритма проследим на примере расчета тока iL):

n

i kL = i kL пр.

+ AkS e S t

(5.10)

S 1

и для его производных

d

m

ikL

d

m

ikLпр

n

S AkS e S t ,

(2.11)

dtm

dtm

S 1

где m=1,2,…(n -1).

9. Определяем токи ikL (0) в индуктивности и их производные:

d mi	kL	,	d m 1i	kL	, …,	di	kL	при t = 0, где m =1,2,…(n-1).
						dt
dt m			dt m 1

10. Определяем постоянные интегрирования. Для этого в уравнениях (5.10) и (5.11) принимаем t = 0 и, подставляя в них соответственно значения тока ikL(0) и его производных при t = 0 , получим систему алгебраических уравнений с неизвестными величинами AkS . Решение этой системы определяет ис-

комые постоянные интегрирования AkS .

11. Используя законы Кирхгофа и уравнения элементов (5.7), определяем токи и напряжения на других участках.

5.4.Расчет переходных процессов в цепях

содним накопителем энергии – индуктивностью

Электромагнитные процессы при переходном процессе в таких цепях обусловлены запасом магнитной энергии в индуктивности и ее рассеиванием в виде тепла на активных сопротивлениях. При составлении дифференциального уравнения следует в качестве неизвестной функции выбрать ток iL в индуктивности. Отметим, что цепи, содержащие всего один участок с накопителем магнитной энергии (L), описываются дифференциальным уравнением первого порядка, т. е. такие уравнения содержат только одну производную diL dt 4 .

При расчете установившегося режима в случае постоянных внешних ЭДС необходимо помнить, что сопротивление индуктивности постоянному току равно нулю.

Ниже рассмотрим несколько примеров, расчет которых выполнен по рекомендованному в разделе 5.1.2 алгоритму.

Пример 5.1. Включение цепи R,L на постоянное напряжение

Последовательная цепь R,L (рис. 5.2,а) R =100 Ом и L=2 Гн подключается к постоянному напряжению U =100 В. Требуется определить ток и напряжение на индуктивности в переходном процессе и построить графики зависимо-

стей iL(t), u L(t).

Решение. 1. Начальное условие iL ( 0) 0, так как цепь до коммутации

была отключена (принимаем, что это было достаточно длительное время).

2. Изображаем электрическую цепь после коммутации (рис.5.2,б) и для нее составляем уравнение по второму закону Кирхгофа:

uL uR U 0 .

(5.12)

а)

б)

i

L

L

uL

U

R

U

R

uR

Рис. 5.2. Включение цепи R,L

Подставляя уравнения элементов (2.7) в уравнение (5.12) и учитывая, что для последовательной цепи i iL , получим

L di dt Ri U.

(2.13)

Уравнение (2.13) – линейное дифференциальное уравнение первого порядка.

3. Решение уравнения (искомый ток переходного процесса) ищем в виде

i iпр iсв.

(2.14)

4.Определяем iпр, который представляет собой установившийся постоянный ток в цепи. Находим его по закону Ома, учитывая при этом, что индуктивное сопротивление при постоянном токе равно нулю:

iпр UR 100100 1 А.

5.Составляем однородное дифференциальное уравнение:

L diсв dt Riсв 0,

решением которого будет функция iсв Ае t .

6. Составляем характеристическое уравнение для определения :

L R 0,

корень которого равен

RL 1002 50 с 1.

Величина 1 0,02 с называется постоянной времени цепи и имеет

размерность времени.
7. Запишем решение (ток в переходном процессе):
i iпр iсв 1 Aе 50t .	(5.15)

8.Согласно первому закону коммутации и начальным условиям

iL ( 0) iL ( 0) i(0) 0.

9.Определим постоянную интегрирования А путем подстановки в уравнение (5.15) t = 0 и, учитывая условие п.8, получим

U

R

0

i(0)

Ae

L

1 Aе

50 0

;

0 1 Ae

50 0

;

A = -1.

R

Ток в переходном процессе

R

i

U

(1

e

L t

50t

А.

(5.16)

R

) 1 е

10. Напряжение на индуктивности можно определить по уравнению

uL U uR U Ri 100 100(1 е 50t ) 100e 50t

В.

Графики зависимостей i(t) и u(t) приведены на рис. 5.3. Отметим, что согласно (5.16) за время, равное , свободная составляющая тока возрастает в е 2,87 раз. Постоянную времени можно определить графически. Для этого к любой точке функции iL проводят касательную, тогда длина подкасательной на

оси времени даст в том же масштабе, что и время, постоянную времени . За длительность переходного процесса принимают время, равное t (4 5) . За

это время величина тока в переходном процессе будет отличаться от установившегося значения тока менее чем на 2 %.

u, B i, A
uL (0) 100
iпр U	1
R				i
50
	0,5
iL ( 0) 0					u	=0,02 с
uL ( 0) 0 0			2	3	4	5	t, с
Установив-		Переходный				Установившийся
шийся ре-			процесс			режим после
жим до ком-						коммутации
мутации
Рис. 5.3. Графики переходных процессов в цепи R,L

Пример 5.2. Короткое замыкание цепи R,L

Рассмотрим случай, когда реальная катушка индуктивности, по которой протекает постоянный ток, замыкается накоротко (рис.2.4,а). Активное сопротивление катушки Rk 100 Ом, R=300 Ом, индуктивность L=2 Гн, U

=100 B. Требуется определить ток iL переходного процесса в индуктивности.

а)

I iL ( 0)

б) iL

в)

iL, A

R

I iL ( 0)

U

RК

RК

uR

0,25

L

L

uL

0

0,04

0,08

0,12 t, с

4

6

Рис. 5.4.

Короткое замыкание цепи R,L

Решение. 1. Определим начальные условия iL ( 0), т. е. установившийся

постоянный ток в цепи (рис. 5.4,а) до коммутации:

iL ( 0)

U

100

0,25 A.

R1

300 100

Rk

2. Для цепи, образовавшейся после коммутации (рис. 5.4,б), составляем уравнение по второму закону Кирхгофа:

uL uR 0.

3. Дифференциальное уравнение будет иметь вид

L didtL Rk iL 0 .

4. Дифференциальное уравнение получили однородным. Поэтому iпр 0 ,5. Ток переходного процесса равен

iL iLсв Ае t .

6. Характеристическое уравнение будет иметь вид

									L Rk			0,
	где		Rk		100	50	1	;		1	0,02 c.
			L		2		с			50

7.Согласно первому закону коммутации

iL ( 0) iL ( 0) U(R1 Rk ) 0,25.

8.Определим постоянную интегрирования А:

iL (0) 0,25 Aе 50 0 ;

А=0,25.

Следовательно, ток iL в катушке равен

iL R1 U Rk е t 0,25е 50t .

На рис.5.4,в приведен график зависимости iL (t).

Проверим энергетические соотношения в цепи. До начала переходного процесса в магнитном поле индуктивности была запасена энергия

	WM		LiL2	( 0)			2	0,252	0,0625 Дж.
				2				2
Энергия, преобразованная за время переходного процесса в тепловую,
равна
		2Rk					2	( 0)L	2
iL2 Rk dt Rk iL2	( 0) е		L	t dt		Rk iL				LiL ( 0)	0,0625 Дж.
0	0						2Rk		2

Таким образом, весь запас энергии магнитного поля перешел в тепловую энергию в сопротивлении Rk .

Коммутационные перенапряжения в индуктивных цепях. Другой серьезной неприятностью, возникающей при разрыве цепей с большей индуктивностью, является появление в этих цепях в процессе разрыва относительно больших напряжений. В отдельных случаях при разрыве индуктивных цепей могут возникать ЭДС, а следовательно, и напряжения, во много раз превосходящие напряжения в цепи при нормальной ее работе. Эти перенапряжения, часто называемые коммутационными перенапряжениями, иногда достигающие многих сотен и даже тысяч вольтов, представляют серьезную опасность для личного состава, обслуживающего эти цепи, а также могут вызвать пробой изоляции в отдельных элементах цепи, в первую очередь в самой катушке.

Разрядные резисторы. Для предотвращения коммутационных перенапряжений параллельно индуктивным катушкам включают так называемые разрядные резисторы (рис. 5.5, а).

Рис. 5.5. Электрические цепи с разрядными резисторами

В этом случае разрыв цепи с помощью ключа К не сопровождается возникновением дуги между его контактами, так как ток I , ранее протекавший по катушке, имеет возможность замкнуться через разрядный резистор RP ; соот-

ветственно этому переходный процесс в цепи протекает аналогично рассмотренному выше случаю замыкания цепи RL накоротко, при котором ток катушки монотонно падает по показательному закону. В первое же мгновение после разрыва цепи этот ток, не успев измениться, создает на разрядном резисторе наибольшее напряжение, равное RP I . Это же напряжение, которое в дальнейшем

будет снижаться по показательному закону из-за соответствующего уменьшения тока, приложено и к отключаемой катушке L.

Таким образом, подбирая сопротивление RP разрядного резистора, мы

можем управлять напряжением, возникающим на катушке при ее отключении. Расчет разрядного резистора осуществляют, задаваясь допустимым коэффициентом перенапряжения, представляющим собой отношение максимального напряжения Umax на катушке, которое можно допустить при ее отключе-

нии, к напряжению U катушки, имеющему место при нормальной ее эксплуатации:

kП UUmax .

Напряжение на катушке в нормальных условиях ее эксплуатации определяется сопротивлением RL обмотки катушки и протекающим по ней током I :

U RL I .

Максимальное напряжение, возникающее на разрядном резисторе, а следовательно, и на катушке, в первый момент размыкания ключа (рис. 5.5) согласно предыдущему уравнению будет равно

Umax RP I .

Отсюда для коэффициента перенапряжения имеем

kП Umax	RP ,
U	RL

и, следовательно, сопротивление разрядного резистора при заданном kП можно рассчитать по формуле

RP kП RL .

Коэффициент перенапряжения, допустимый для данного электрооборудования, зависит от его сложности, от требуемой степени надежности установ-

ки, от уровня ее номинального напряжения и обычно лежит в пределах

1,5 kП 3 .

Включение разрядных резисторов непосредственно на зажимы катушек, как показано на рис. 5.5, а, применяется относительно редко, так как при этом происходит непродуктивная затрата энергии на нагрев разрядного резистора током, протекающим по нему при включенной цепи.

Вмощных цепях разрядные резисторы присоединяются к катушке специальными коммутационными аппаратами непосредственно перед отключением цепи. Последовательность действия такого аппарата, схематично показанного на рис. 5.5, б в виде ключа, такова, что контактной пластинкой К при ее повороте в направлении стрелки вначале осуществляется замыкание катушки на резистор, а уже затем отключение цепи от источника.

Вмаломощных цепях резисторы обычно включаются через полупроводниковые вентили. При соответствующей полярности включения вентиля (рис. 5.5, в) ток через разрядный резистор при включенной цепи протекать не может. После же ее отключения ток катушки свободно замыкается через разрядный резистор.

Вряде случаев в качестве разрядных резисторов используют вариаторы, включая их непосредственно на зажимы катушки (рис. 5.5, а). Если нормальное напряжение U катушки будет ниже колена на характеристике варистора (рис. 5.6), то ток через варистор при включенной цепи протекать практически не будет. После же отключения цепи напряжение на варисторе не может подняться выше уровня U max , так как при этом напряжении через варистор свободно

замкнется любой ток катушки.

Об экстратоках размыкания. В практической электротехнике нередко оперируют термином «экстраток размыкания», подразумевая под ним ударный коммутационный ток, но возникающий не в емкостной, а в индуктивной цепи.

Поскольку скачкообразного изменения тока в самой катушке произойти не может, то экстратоки размыкания возникают лишь в резистивных ветвях, включенных параллельно катушкам. Примером такой ветви может служить ветвь разрядного резистора на рис. 5.5, а, ток в котором при отключении катушки на мгновение становится равным первоначальному току катушки и может оказаться во много раз превосходящим ток резистора в нормальном режиме цепи.

U

Umax

U

Рис. 5.6. Характеристика варистора

Если в цепи катушки разрядного резистора нет, но к ней присоединен вольтметр (рис. 5.7), то экстраток при размыкании цепи протечет по вольтметру, который может быть при этом даже поврежден, так как в вольтметре выделится вся энергия, ранее запасенная в магнитном поле катушки.

Рис. 5.7. Электрическая схема, при размыкании которой может быть поврежден вольтметр

Включение цепи RL под синусоидальное напряжение. Установившийся ток в цепи RL при ее питании от источника с синусоидальным напряжением

u Um sin t u

также является синусоидальной функцией времени i Im sin t u .

Поэтому общее решение дифференциального уравнения, описывающее переходный процесс в цепи RL, в этом случае будет иметь вид

i i Aexp t Im sin t u Aexp t .

Используя очевидное начальное	условие в рассматриваемой задаче
i 0 0, для постоянной интегрирования	получим

0 Im sin u A или A Im sin u .

Тогда окончательно ток переходного процесса запишется в виде i i i Im sin t u Im sin u exp t ,

где, напоминаем, первое слагаемое представляет собой установившийся ток i , а второе слагаемое — свободный ток i .

Обращаем внимание на то, что свободный ток, несмотря на то, что в его выражение входит синус, представляет собой чисто показательную функцию, так как аргумент этого синуса ( u ) является постоянной величиной.

О зависимости переходного процесса от момента включения цепи.

Характерной особенностью полученного решения является присутствие в нем начальной фазы u питающего напряжения. Поскольку время в рассматривае-

мой задаче отсчитывается от момента включения цепи, то и фаза напряжения также должна рассматриваться относительно этого момента и, следовательно, начальная фаза u представляет собой фазу питающего напряжения в момент включения цепи. Для уяснения этой мысли на рис. 5.8, где в зависимости от двух аргументов (t и t ) построена кривая синусоидального питающего напряжения, отмечен ряд моментов включения цепи (O1, O2 , O3 ) и показаны со-

ответствующие начальные фазы напряжений ( u1 = 90°, u 2 = – 45°, u3 = 0).

Присутствие начальной фазы в аналитическом выражении переходного процесса показывает, что течение этого процесса будет зависеть от того, в какой момент, то есть при какой фазе напряжения, будет включена цепь. В частности, если цепь RL (рис. 5.8, а) включить, когда фаза напряжения равна фазовому углу ( u ), то переходного процесса не возникнет вовсе, и в цепи с

первого момента включения наступит установившийся режим. Это вытекает из того, что при указанном условии множитель sin u в выражении для пере-

ходящего тока, а следовательно, и сам свободный ток обращаются в ноль. Графически процесс включения цепи RL при этом условии представлен на рис. 5.8,

б.

Заметим, что угол u i в общем случае представляет собой начальную фазу установившегося тока, поэтому включение цепи в момент, когдаu , соответствует условию ее включения в момент, когда начальная фаза

установившегося тока равна нулю (рис. 5.8, б).

t

Ψu1 Ψu2

Рис. 5.8. Кривая питающего напряжения

Общий случай переходного процесса. Для построения кривой тока пере-

ходного процесса в общем случае, то есть при произвольном моменте включения цепи, заранее нанесем на график вместе с кривой напряжения также и кривую установившегося тока i (рис. 5.9, в), сдвинутую относительно напряжения на угол (для удобства построения кривых ось абсцисс целесообразно снабдить двумя шкалами - временной t и угловой t ). Выбрав на оси абсцисс момент включения цепи (t = 0), пометим соответствующие значения начальных фаз u и i u .

Возвращаясь далее к аналитическому выражению тока переходного про-

цесса

i i i Im sin t u Im sin u exp t ,

обратим внимание, что при t = 0 значения установившегося i и свободного i токов равны по величине и обратны по знаку:

i 0 i 0 Im sin u Im sin i .

Поэтому экспонента свободного тока i должна начаться из конца отрезка оси ординат, равного значению установившегося тока в момент t = 0, но отложенного в противоположную сторону оси (рис. 5.9, в). Ориентируясь на постоянную времени цепи L / R , строим кривую свободного тока i и, суммируя ее с кривой установившегося тока i , получаем графическое изображение зависимости тока переходного процесса от времени (толстая кривая на рис. 5.9, в).

Заметим, что условие равенства абсолютных значений установившегося и переходящего токов в начальный момент времени очевидно не только из анализа приведенного выше выражения для тока переходного процесса. Оно неизбежно вытекает из физического представления о том, что действительный ток, равный сумме установившегося и свободного токов, должен быть в момент t 0 равен нулю (начальное условие).

Как вытекает из выполненного построения, действительный ток i переходного процесса сперва значительно отличается от установившегося тока i , однако с течением времени по мере затухания свободного тока i кривая тока i все ближе и ближе подходит к кривой установившегося тока i , стремясь в дальнейшем влиться в нее полностью.

Характерным при включении цепи RL под синусоидальное напряжение является возникновение спустя примерно полупериод так называемого ударного тока включения I уд (рис. 5.9, б), превосходящего по своей величине даже

максимальный ток Im установившегося режима цепи.

Наиболее неблагоприятный случай включения цепи RL. Поинтересуем-

ся условиями, при которых ударный ток включения цепи RL под синусоидальное напряжение приобретает наибольшее значение.

Очевидно, что это случится тогда, когда наибольшей величины достигнет свободный ток i . Последнее же будет иметь место, если момент включения цепи совпадет с моментом максимума установившегося тока i (рис. 5.9, г), то есть начальная фаза i установившегося тока будет равна i 0,5 , а начальная

фаза питающего напряжения u 0,5 . При этом максимум тока переход-

ного процесса наступает спустя полупериод от момента включения цепи. Если к тому же цепь будет обладать значительной постоянной времени L / R , во много раз превосходящей период Т приложенного к цепи напряжения, то затухание свободного тока в течение первого полпериода переходного процесса практически будет незаметным и ток i переходного процесса изобразится синусоидой, целиком опущенной под ось абсцисс (см. рис. 5.9, д). Поэтому в пределе ударный ток может достигнуть удвоенной амплитуды тока установившегося режима ( I удmax 2Im ).

Рис. 5.9. Формы кривых токов переходного процесса при разных начальных фазах питающего напряжения

Заметим, что удвоение тока при включении цепи в большинстве случаев не представляет для нее какой-либо опасности: с тепловым эффектом в этом

случае можно вообще не считаться, так как увеличение тока весьма кратковременно, а механические силы, возникающие под действием этого тока, хотя и возрастут в четыре раза (силы пропорциональны квадрату тока, но не вызовут поломки, так как коэффициент запаса прочности у электротехнических установок редко бывает ниже этой величины.

5.5. Расчет переходных процессов в цепях с одним накопителем энергии - емкостью

Электромагнитные процессы при переходном процессе в таких цепях обусловлены запасом электрической энергии в емкости С и рассеиванием этой энергии в виде тепла на активных сопротивлениях цепи. При составлении дифференциального уравнения следует в качестве неизвестной функции выбрать напряжение uC на емкости. Следует отметить, что при расчете установившихся режимов, т. е. при определении начальных условий и принужденной составляющей, сопротивление емкости в цепях постоянного тока равно бесконечности.

Рассмотрим ниже несколько примеров.

Пример 2.3. Включение цепи R,C на постоянное напряжение

Цепь (рис. 5.10,а), состоящая из последовательно соединенных сопротивления R = 1000 Ом и емкости С = 200 мкФ, в некоторый момент времени подключается к постоянному напряжению U=60 В. Требуется определить ток и напряжение емкости в переходном процессе и построить графики uC (t), i(t).

а)

б)

в)

R

i

R

i, A u, B

60

uR

0,06

uC

U

C

U

uC

C

= 0,02,c

uC ( 0)

i

2 3 t,с

Рис. 5.10. Включение цепи R,C на постоянное напряжение Решение. 1. Начальное условие uC (-0) = 0, так как цепь до коммутации

была отключена (полагаем достаточно длительное время).

2. Изображаем электрическую цепь после коммутации (рис. 5.10,б) и для нее составляем уравнение по второму закону Кирхгофа:

uR uC U 0 или

Ri uC U .

3. Преобразуем уравнение п.2 в дифференциальное. Для этого, подставив вместо тока i известное уравнение i C duC dt , получим

RC dudtC uC U.

4. Решение уравнения (искомое напряжение на емкости) ищем в виде

uC uСпр uСсв .

5. Определяем uСпр . Так как в цепи постоянного тока в установившемся

режиме сопротивление емкости равно бесконечности (при этом Ri 0 ), то все напряжение будет приложено к емкости. Поэтому

uCпр =U = 60 В.

6. Составляем однородное дифференциальное уравнение

RC

duСсв

uСсв 0,

dt

решением которого будет функция

uСсв Aе t .

7. Составляем характеристическое уравнение RC + 1= 0, корень которого

равен

1

1

5

1 .

RC

2 10 4

103

с

Постоянная времени

1

RC

1 0,2

c.

5

8. Запишем решение:

uC

uСпр

uСсв U Aе t .

9. Согласно второму закону коммутации и начальным условиям

uC ( 0) uC ( 0) uC (0) 0.

10. Определим постоянную интегрирования А путем подстановки t=0 в

уравнение п.8:

uC (0) U A;

A U.

Напряжение на емкости в переходном процессе

uC U Ue t U (1 е t ) 60(1 е 5t ) В.

11. Ток в цепи можно определить по уравнению i C duC dt

или по уравнению п.2.

i	U uC		U U (1 е t )		U	е	t	0,06е	5t	А.
	R		R		R

Графики uC (t) и i(t) представлены на рис. 5.10,в.

Пример 2.5. Короткое замыкание цепи R,C

В цепи (рис. 5.11,а)

происходит замыкание. Известны: R1 =100 Ом,

R2 =3 Ом, С = 200 мкФ, постоянное напряжение U = 60 B. Требуется определить

напряжение uC при переходном процессе.

а)

б)

u,B

i, A

R1

R2

uC ( 0)

U

U

uC

iC ( 0)

0

C

uC

0

t, c

iC

iC ( 0)

U

R2

Рис. 5.11. Замыкание цепи R,C

Решение. Задачу можно решить, используя свойство дуальности соотношений

	uL L	di	и iC C	duC	.
		dt		dt

Дифференциальные уравнения, описывающие переходные процессы в цепи R,L и дуальной цепи R,C, будут также дуальны. Например, при включении цепи R,L (рис. 5.2,а) и цепи R,C (рис. 5.10,а) на постоянное напряжение были получены дуальные уравнения и соответственно их дуальные решения:

	L	diL		RiL U ;		iL	U	(1 е	t	);
		dt					R
	RC		duC		uC U ;	uC U (1 е t ) .
			dt

Поэтому, воспользовавшись результатами при расчете переходного процесса цепи R,L для случая короткого замыкания и свойством дальности, запишем напряжение uC на емкости для случая короткого замыкания в виде

uC Aе	t	;	iC	U	е	t	,
				R2

где А = U ; 1R2C .

Указанные выражения для А и студентам предлагается вывести самостоятельно. Графики зависимостей uC (t) и iC (t) представлены на рис. 2.8,б.

Проверим энергетические соотношения. До начала переходного процесса в электрическом поле конденсатора была запасена энергия WЭ CU2 2 .

Энергия, перешедшая за время переходного процесса в тепловую, равна

2		U	2	2t		U 2CR2			2t				CU 2		CU 2
				R C					R C
	iC R2 dt	R	е	2	dt			е	2					(0 1)		.
						2R							2		2
			2				2
0		0									0

Таким образом, весь запас энергии электрического поля перешел в тепловую энергию в сопротивлении R .

5.6. Переходные процессы в цепи RLC

Цепь RLC и ее дифференциальное уравнение. При питании цепи RLC от источника с напряжением u уравнение, записанное для нее по второму закону Кирхгофа при принятых на 5.12 положительных направлениях, имеет вид

Ri uC u eL .

Выражая ЭДС самоиндукции eL через ток i цепи: eL L dd ti ,

после некоторой перегруппировки членов уравнения получим

L dd ti R i uC u .

i

uL

uC

Рис. 5.12. Электрическая цепь с элементами RLC

Для исключения отсюда напряжения uC на конденсаторе продифференцируем уравнение по времени:

L	d 2 i		R	d i		d u	C		d u
	d t	2		d t					d t
						d t

и примем во внимание, что

uC qCC

и, следовательно,

d uC	1	d qC	i	,
			C
d t	C d t

так как производная от заряда qC конденсатора равна току i .

Тогда уравнение, описывающее переходный процесс в цепи, будет содержать только ток цепи:

	L	d 2 i		R	d i		i		d u	.
		d t	2		d t		C		d t

В отличие от предыдущих задач здесь мы встречаемся с линейным дифференциальным уравнением второго порядка.

Общее решение дифференциального уравнения рассматриваемой цепи представится по общему правилу суммой

i i i

установившегося тока i цепи и свободного тока i , представляющего собой решение соответствующего однородного дифференциального уравнения:

	L	d 2 i	R d i		i	0 .
		d t2			C
			d t

Для его же решения необходимо по данному дифференциальному уравнению составить характеристическое уравнение

L 2 R C1 0

или

2 RL LC1 0

и определить его корни:

		R			R		2	1		2	02 ,
1,2
		2L						LC
					2L

где и 0 — часто употребляемые сокращенные обозначения величин

		R	,	0		1	,
		2L				LC

вторая из которых представляет собой резонансную угловую частоту рассматриваемой цепи.

При различающихся корнях решение однородного уравнения будет иметь

вид

i A1 exp 1t A2 exp 2t ,

где A1 и A2 — произвольные постоянные интегрирования.

При равных корнях 1 2 (в случае 0 ) решение од-

нородного уравнения должно быть записано в виде

i (A3 A4t) exp t (A3 A4t) exp t ,

где A3 , A4 также являются произвольными постоянными интегрирования.

Следует заметить, что в первом случае решения характер переходного процесса, в свою очередь, может быть двояким в зависимости от того, будут ли корни характеристического уравнения вещественными (при 0 ) или ком-

плексными (при 0 ). При вещественных корнях, оба из которых, как не-

трудно установить, будут отрицательными, в решение уравнения войдут две показательные монотонно убывающие функции, определяющие собой так называемый апериодический характер переходного процесса. В случае комплексных корней процесс приобретает колебательный характер, так как показательная функция с комплексным показателем представляет собой синусоидальную функцию с переменной амплитудой.

В соответствии с изложенным анализ переходных процессов в цепи RLC проводят в трех вариантах, соответствующих трем различным по характеру значениям корней характеристического уравнения (различных вещественных, различных комплексных и равных вещественных).

Разрядка конденсатора на цепь RL. В качестве простейшего примера переходного процесса в цепи RLC рассмотрим разрядку конденсатора на последовательно соединенные резистор R и катушки L(рис. 5.13, а). После замыкания ключа К конденсатор С, предварительно заряженный до напряжения uC UC0 ,

начинает разряжаться. Переходный процесс будет протекать до тех пор, пока весь запас энергии конденсатора полностью не превратится в тепловую энергию, выделившуюся в резисторе. Тогда электромагнитный процесс в цепи полностью затухнет, и ее ток спадет до нуля. Таким образом, установившийся ток в рассматриваемой задаче следует признать равным нулю (i 0 ), и ток переходного процесса будет равен только его свободной составляющей:

i i i i

Начальные условия. Для конкретизации общего решения дифференциального уравнения, на каком бы характере переходного процесса мы ни желали остановиться, необходимо определить произвольные постоянные интегрирования по начальным условиям. Таковыми в рассматриваемой задаче будут начальные значения тока i 0 катушки и напряжения uC 0 конденсатора. По-

скольку ни ток катушки, ни напряжение конденсатора мгновенно измениться не могут, в качестве начальных условий принимаем значения этих величин непосредственно перед началом переходного процесса, то есть

i 0 0 , uC 0 UC0 .

Если первое из этих условий может быть использовано непосредственно, так как само уравнение и его решение записаны относительно тока, то второе начальное условие требует некоторого преобразования, с тем чтобы из него получить начальное значение первой производной тока, как этого требует классическая математика.

Для этого обратимся к исходному уравнению цепи и, памятуя, что в рассматриваемой задаче приложенное к ней напряжение u равно нулю, перепишем его в виде

Ri uC eL или	Ri uC L	d i	.
		d t

Это уравнение, записанное для начального момента времени, то есть ко-

гда i 0 , приводит к равенству
uC	d i		,
	L
	d t	0

откуда для второго начального условия имеем

d i			U	C0
					.
			L
d t		0

Апериодический процесс. Как было указано выше, этот характер переходного процесса имеет место при условии 0 , когда корни

1,2 2 02

характеристического уравнения вещественны и различны. Вспоминая ранее принятые обозначения

		R	и 0	1
		2L		LC

и раскрывая упомянутое условие 0 , убеждаемся, что апериодический ха-

рактер разрядки конденсатора имеет место при относительно большом сопротивлении резистора:

R 2LCL 2 CL 2 ,

превосходящем удвоенное характеристическое сопротивление цепи RLC.

В этом случае решение для тока следует искать в виде i i A1 exp 1t A2 exp 2t .

Использование первого начального условия (равенство нулю начального тока) приводит нас к результату

0 A1 A2 или A2 A1 ,

и, следовательно, для тока цепи имеем

i A1[exp 1t exp 2t ].

t

UC0

t

UC0

Рис. 5.13. Разрядка конденсатора на цепь RL

Чтобы использовать второе начальное условие, необходимо предварительно получить выражение для производной от тока:

dd ti A1[ 1 exp 1t 2 exp 2t ] ,

подставляя в которое второе начальное условие, получим

	UC0	A				или	A	U C0	.
	L	1	1		2		1	1 2 L

Принимая во внимание, что

1 2 2 2 02 ,

для постоянной интегрирования A1 имеем

	A1			UC0		.
			2L	2	02

Тогда для тока в цепи окончательно получим

	i		UC0		[exp 1t exp 2t ].
		2L	2	02

Так как 2 02 , то оба корня характеристического уравнения явля-

ются отрицательными и каждая из показательных функций, входящих в выражение для тока, графически представляется в виде экспоненты (рис. 5.13, б), причем первая будет уменьшаться медленнее второй, поскольку 1 2 , и,

следовательно, постоянная времени 1/ 1 первой функции больше постоянной времени второй 1/ 2 .

Зависимость тока разрядки конденсатора от времени определяется разностью упомянутых показательных функций, то есть разностью ординат построенных на рис. 5.13, б экспонент (заштрихованная область). Таким образом, кривую тока цепи при переходном процессе с учетом минуса перед его аналитическим выражением можно изобразить, как показано на рис. 5.13, в, толстой линией.

Отрицательные значения тока в течение всего переходного процесса свидетельствуют, что ток течет в направлении, обратном указанному на схеме рис. 5.13, а. Это согласуется с физическим представлением о процессе разрядки, так как при положительном начальном напряжении на конденсаторе, что предполагалось по условию задачи, правая на схеме обкладка конденсатора имеет более высокий потенциал, и ток разрядки потечет через катушку и резистор именно от этой обкладки к противоположной.

Весьма характерно, что ток разрядки конденсатора через катушку не претерпевает скачков, как это имело место при разрядке конденсатора через один резистор (рис. 5.11, в). На этот раз он плавно нарастает (по абсолютной величине) до некоторого максимального значения, а затем монотонно падает, стремясь в пределе к нулю.

Не приводя доказательства (желающим это предоставляется гделать самостоятельно), заметим, что точка n перегиба кривой тока находится на двойном расстоянии 2tm от оси координат по сравнению с точкой m максимума то-

ка (рис. 5.13).

Напряжения в цепи при апериодическом процессе. Напряжениями на резисторе, катушке и конденсаторе мы поинтересуемся, не обращаясь к их развернутым аналитическим выражениям в функции времени, а ограничившись

построением их кривых, исходя из общих зависимостей между напряжениями и током.

Напряжение на резисторе на основании закона Ома uR Ri

будет пропорционально току в цепи и изобразится кривой, подобной кривой тока (кривая uR на рис. 5.17, в).

Напряжение на катушке в соответствии с известным выражением uL eL L dd ti

можно построить как производную тока. В частности, в момент tm максимума тока напряжение uL обратится в нуль (см. кривую uL на рис. 5.17, в), а в точке перегиба кривой тока (при t 2tm ) оно будет иметь максимум. В начальный

момент времени, как следует из уравнения напряжений по контуру цепи (2-й закон Кирхгофа)

uR uL uC 0 ,

напряжение на катушке будет по величине равно напряжению конденсатора, так как uR 0 0 и противоположно ему по знаку:

uL 0 uC 0 UC0 .

Кривую напряжения на конденсаторе можно построить, начиная от его значения uC 0 UC0 , руководствуясь связью

i C ddutC ,

то есть рассматривая ток как производную напряжения uC . Поэтому в начальный момент, когда ток равен нулю, кривая напряжения uC имеет максимум, и, следовательно, она отходит от оси ординат горизонтально, склоняясь затем вниз (кривая uC на рис. 5.17, в). Точка n перегиба этой кривой соответствует моменту tm , когда ток разрядки приобретает максимальное значение. Физиче-

ски это означает, что процесс разрядки в указанный момент достигает наибольшей интенсивности и поэтому наблюдается наибольшая скорость снижения напряжения конденсатора (кривая uC идет вниз наиболее круто). Так как

напряжение uL на катушке в этот момент равно нулю, то, как следует из написанного выше уравнения напряжений, напряжение конденсатора при t tm должно по абсолютной величине равняться напряжению uR на резисторе. Далее

скорость спадания напряжения конденсатора замедляется, и кривая uC идет все

более и более полого, асимптотически приближаясь к оси абсцисс.

Энергетические явления при апериодическом процессе разрядки кон-

денсатора в первую очередь характеризуются непрерывным уменьшением запаса энергии в электрическом поле конденсатора, определяющегося его напряжением

WЭ 12 C uC2

и расходом энергии на необратимый процесс преобразования электромагнитной энергии в тепло в резисторе. Скорость этого процесса определяется мгновенной мощностью

p Ri2 ,

которая достигает наибольшего значения в момент максимума тока.

Вместе с тем нельзя игнорировать роль катушки в энергетическом балансе цепи. Энергия, запасенная в ее магнитном поле, зависит от тока катушки:

WM 12 Li2 ,

поэтому в интервале от 0 до момента tm , пока ток непрерывно нарастает (рис. 5.13, в), происходит временное накопление энергии в катушке, куда она поступает опять-таки из разряжающегося конденсатора. Начиная с момента tm и до

окончания переходного процесса ток в цепи непрерывно падает и энергия магнитного поля катушки уменьшается. С этого момента электромагнитная энергия, преобразующаяся в резисторе в тепло, поступает в него как из конденсатора, так и из катушки.

Описанные перетоки энергии в цепи условно показаны жирными стрелками на рис. 5.14, где помечены также действительные направления тока и напряжений на отдельных элементах цепи. На рис. 5.14, а продемонстрированы процессы в начальный интервал разрядки конденсатора до момента tm , а на

рис. 5.14, б - в течение остального времени.

Обратим внимание, что изменение направления потока энергии в катушке в момент tm совпадает с изменением направления на-ней: пока напряжение uL

совпадает с направлением тока в катушке (рис. 5.14, а), она поглощает энергию, то есть играет роль приемника электромагнитной энергии, когда же напряжение и ток катушки оказываются направленными навстречу друг другу (рис.

5.14, б), она начинает отдавать энергию, выполняя функцию источника. В противоположность этому разряжающий конденсатор и резистор не меняют своих функций в течение всего переходного процесса, причем первый из них все время играет роль источника, а второй — приемника электромагнитной энергии.

Рис. 5.14. Энергетические явления при апериодическом процессе

Колебательный процесс разрядки конденсатора имеет место при условии 0 , то есть при относительно малых значениях сопротивления R ,

именно когда оно меньше удвоенного характеристического сопротивления цепи:

R 2 CL 2 .

В этом случае комплексные корни характеристического уравнения удобно записать сокращенно:

1,2 2 02 j 02 2 j ,

где

02 2 .

Тогда общее выражение для тока представится в виде

ii A1 exp 1t A2 exp 2t A1 exp j t A2 exp j t exp t .

Обращаясь к известной связи показательной формы комплексного числа с

тригонометрической

exp j t cos t j sin t ,

выражение в скобках можно преобразовать к виду

A1 exp j t A2 j t A1 A2 cos t j A1 A2 sin t .

Тогда, вводя новые произвольные постоянные

A A1 A2 и

A j(A1 A2 ) ,

общее выражение для тока можно выразить через тригонометрические функции вещественных переменных:

i A cos t A sin t exp t .

Для определения постоянных интегрирования обращаемся к начальным условиям, первое из которых i 0 0 приводит к значению A 0 и, следовательно, позволяет записать решение в сокращенном виде:

iA sin t exp t .

Вцелях реализации второго начального условия

d i			U	C0
			L
d t 0

получим производную от тока по времени

dd ti A exp t cos t A exp t sin t

и подставим в нее оговоренное начальное условие, что приведет к равенству

ULC0 A ,

откуда

A UC0 .L

Следовательно, для тока переходного процесса окончательно имеем

i UC0 exp t sin t .

L

Таким образом, ток в цепи будет изменяться по синусоидальному закону с постепенно уменьшающейся амплитудой (множитель exp t ), что и свиде-

тельствует о затухающем колебательном процессе разрядки конденсатора. Для построения кривой тока нанесем с обеих сторон оси абсцисс ограни-

чивающие кривые UCl0 exp t (штриховые линии на рис. 5.15, а) и между

ними заключим затухающую синусоиду sin t с периодом T 2 / .

Через четверть периода от начала координат кривая тока коснется нижней ограничивающей, а через полупериод она пересечет ось абсцисс, с тем чтобы

через три четверти периода вновь коснуться, на этот раз верхней ограничивающей.

Скорость затухания и частота колебаний. Скорость затухания колеба-

тельного процесса разрядки конденсатора, как вытекает из аналитического выражения для тока i и его графического построения, зависит от величины

2RL ,

называемой коэффициентом затухания.

а)

UC0

L

UC0

L

б)

UC0

UC0

Рис. 5.15. График колебательного процесса разрядки конденсатора

Чем меньше эта величина, то есть чем меньше сопротивление R цепи, тем медленнее будут затухать колебания тока. В предельном случае, когда сопротивление R обратится в нуль, в цепи наступит незатухающий колебательный процесс, амплитуда колебаний тока в котором будет оставаться неизменной.

Угловая частота колебательного процесса разрядки конденсатора

02 2 LC1 2RL

также зависит от сопротивления цепи и в реальных условиях оказывается меньше резонансной угловой частоты 0 этого контура. Лишь при незатухаю-

щем процессе в сверхпроводящем контуре частота колебаний равна резонансной частоте, что послужило причиной называть ее также частотой незатухающих колебаний.

Следует заметить, однако, что отличие частоты затухающих колебаний от частоты незатухающих колебаний в подавляющем большинстве случаев весьма незначительно и не имеет практического значения. Лишь когда коэффициент затухания приближается к 0 , различие частот и 0 становится замет-

ным, но в этом случае затухание процесса оказывается настолько сильным, что колебательный процесс практически вырождается.

Напряжения в цепи при колебательном процессе также будут изме-

няться по синусоидальному закону с затухающей амплитудой.

Кривая напряжения на резисторе в соответствующем масштабе повторит кривую тока (рис. 5.15, б), так как

uR Ri .

Кривые напряжений uL на катушке и uC на конденсаторе начнутся на оси ординат из точек с ординатами UC0 и UC0 . Их построение мы выполним, ориентируясь на построенную кривую тока i и очевидные соотношения

uL L	d i	и	i C	d uC	.
	d t
				d t

При этом кривая напряжения uL на катушке будет пересекать ось абсцисс

не в моменты, кратные четверти периода, а несколько раньше, так как максимумы кривой тока, определяющейся функцией

exp t sin t

наступают немного раньше максимумов чистого синуса (рис. 5.15, б). Соответственно раньше моментов пересечения кривой тока с осью абсцисс наступают и максимумы напряжения uL .

В противоположность этому напряжение uC на конденсаторе проходит

через нуль несколько позже моментов, кратных T / 4 . Максимумы же напряжения на конденсаторе точно совпадают с нулями тока, так как последний определяется производной от напряжения uC .

Периодическое изменение знака напряжения uC на конденсаторе свидетельствует, что колебательный процесс разрядки конденсатора на цепь RL со-

провождается его периодической перезарядкой. При этом максимальные напряжения, до которых заряжается конденсатор, с каждой перезарядкой все уменьшаются и уменьшаются, стремясь в пределе по истечении бесконечно большого времени к нулю.

Энергетические явления при колебательном процессе значительно сложнее таковых при апериодическом процессе и протекают, периодически повторяясь через каждый полупериод колебаний. Поэтому мы рассмотрим их только за первый полупериод после начала переходного процесса, сопровождая анализ иллюстрацией направлений потоков энергии и действительных направлений токов и напряжений в цепи (рис. 5.16). Напомним, что до замыкания цепи ток в ней отсутствовал и вся энергия была сосредоточена в заряженном до напряжения UC0 конденсаторе.

Рис. 5.16. Энергетические явления при колебательном процессе

В начальный интервал времени от момента замыкания ключа до момента максимума тока (интервал t1 на рис. 5.15, б) разрядка конденсатора сопровож-

дается нарастанием тока в цепи и, следовательно, запасанием энергии в магнитном поле катушки. Эта энергия поступает в катушку из разряжающегося конденсатора, который одновременно посылает энергию и в резистор, где она с нарастающей мощностью преобразуется в тепло и рассеивается в окружающее пространство (рис. 5.16, а).

В следующий относительно короткий интервал времени t2 (рис.

5.15, б) до момента перехода напряжения конденсатора через нуль последний продолжает разряжаться, питая резистор энергией, освобождающейся в конденсаторе. Катушка, ток i в которой в этот интервал времени начал падать, также отдает резистору накопленную в ней перед этим энергию (рис. 5.16, б).

В третий интервал времени, в течение которого ток i резко падает до нуля (интервал t3 на рис. 5.15, б), энергия, освобождающаяся в катушке, доста-

точна и для питания резистора, и на перезарядку конденсатора. В последнем легко убедиться по напряжению на конденсаторе, которое в рассматриваемом интервале, изменив знак, возрастает, свидетельствуя о новом накоплении энергии в электрическом поле конденсатора (рис. 5.16, в).

По завершении третьего интервала конденсатор оказывается заряженным до максимума напряжения противоположной полярности, и с момента T / 2 (рис. 5.15, б), когда ток, пройдя нулевое значение, вновь станет возрастать, энергетические процессы полностью повторятся, но с изменившимися на обратные направлениями тока и напряжений.

Граничный случай разрядки конденсатора на цепь RL соответствует ус-

ловию 0 , которое приводит к равенству

R 2 CL 2

сопротивления R резистора удвоенному характеристическому сопротивлениюцепи, а также к двум одинаковым корням характеристического уравнения:

1 2 .

Решение дифференциального уравнения в этом случае следует искать в

виде

i i A3 A4t exp t .

Использование первого начального условия i 0 0 дает возможность определить постоянную интегрирования A3 0.

Продифференцировав уточненное решение i A4t exp t

по времени

dd ti A4 exp t A4t exp t

и используя второе начальное условие
d i			U	C0
					,
			L
d t		0

получим возможность определить вторую постоянную интегрирования:

ULC0 A4

и записать окончательное выражение для тока переходного процесса: i ULC0 t exp t .

Для выяснения характера полученной зависимости запишем ее в виде

iULC0 (t / exp t )

ипостроим элементы этой функции t и exp t (рис. 5.17).

tm

Рис. 5.17. График тока разрядки при условии 0

Так как при малых значениях t знаменатель растет медленнее числителя, ток i сначала возрастает. При t tm , когда скорость возрастания знаменателя

сравняется со скоростью возрастания линейной функции (штриховая прямая), ток достигает максимума. Затем показательная функция обгоняет линейную функцию, и дробь t / exp t начинает уменьшаться, стремясь к нулю при без-

граничном увеличении времени.

Таким образом, кривая тока i переходного процесса разрядки конденсатора при граничных условиях по форме аналогична кривой тока при апериодическом процессе (см. рис. 5.17, б).

То же можно сказать и о кривых напряжений на резисторе, катушке и конденсаторе, которые при граничном условии качественно не будут отличаться от соответствующих кривых, построенных на рис. 5.17, б. Иными словами, граничный случай переходного процесса, несмотря на своеобразие математического решения, по существу, представляет собой частный случай апериодического процесса.

Длительность процесса разрядки конденсатора удобнее всего оценить по изменению напряжения uC на конденсаторе, которое в начале переходного процесса является заданной величиной, не зависящей от условий разрядки.

Аналитические выражения для напряжения uC на конденсаторе при различных условиях разрядки найдем, опираясь на полученные выше выражения

для тока i

в цепи на основании второго закона Кирхгофа:

uC uL uR L

d i

Ri .

d t

При апериодическом процессе, когда ток выражается в виде

i

UC

0

[exp 1t exp 2t ]

2L 2

02

для напряжения на конденсаторе имеем

uC

L

UC0

[ 1 exp 1t 2

exp 2t ] R

UC0

2L 2

02

2L 2 02

UC0

R

R

[exp 1t

exp 2t ]

[ 1

exp 1t

2

exp 2t ]

02

2 2

1

L

L

U C0

[ 1 exp 2t 2

exp 1t ],

2

02

2

так как

1

R

R

2

02

R

R

2 02 2 ;

L

2L

L

2L

2

R

R

2

02

R

R

2 02 1.

L

2L

L

2L

Поскольку

1

2

и

функция

exp 2t

убывает

скорее функции

exp 1t (см. рис. 5.17, б), то, как следует из последнего выражения для uC , практическое окончание переходного процесса будет определяться остаточным

значением функции exp 1t , то есть временем

51/ 1

. При этом, чем больше

значение

R

R

2

1

2 02 ,

1

2L

2L

LC

тем скорее заканчивается переходный процесс. Наибольшее значение 1 соответствует граничному условию 0 , то есть

R 2 CL 2 ,

когда подкоренное выражение обращается в нуль. Поэтому наиболее быстро конденсатор разряжается именно при этом условии. Всякое увеличение сопротивления резистора, по сравнению с двойным характеристическим сопротивлением 2 цепи, влечет за собой затягивание процесса разрядки конденсатора.

На рис. 5.18 представлены три кривые напряжения конденсатора при апериодическом процессе разрядки, соответствующие трем значениям R / 2L и наглядно показывающие зависимость скорости разрядки от сопротивления R.

Уменьшение сопротивления ниже значения R 2 , которое соответствует граничному условию 0 , приводит еще к более быстрому снижению напряжения конденсатора (см., например, кривую при 0,5 0 на рис. 5.18), од-

нако это сопряжено с переходом апериодического процесса в колебательный, при котором переходный процесс вновь затягивается. Действительно, колебательному процессу соответствует выражение для тока

					i UC0			exp t sin t ,
							L
при котором напряжение на конденсаторе можно представить в виде
uC L			d i	R i L	UC0	exp t sin t exp t cos t
			d t
					L
R	UC0	exp t sin t					U C0	R L sin t L cos t exp t .
							L
	l

Рис. 5.18. Кривые напряжения конденсатора при апериодическом процессе разрядки

Выражение в квадратных скобках представляет собой синусоидальную функцию с угловой частотой , поэтому длительность переходного процесса будет определяться скоростью спадания амплитуд этих синусоид, то есть функ-

цией exp t . Через время, равное 5 1, мы будем считать переходный про-

цесс практически закончившимся. И чем меньше R / 2L , то есть чем меньше сопротивление R цепи, тем дольше будет затягиваться переходный процесс. В пределе при R 0 наступает незатухающий колебательный процесс, длящийся бесконечно долго. На рис. 5.18 построены две кривые напряжения конденсатора, соответствующие колебательному процессу разрядки при двух различных значениях ( 0,5 0 и 0,2 0 ) и наглядно иллюстрирующие затягивание

переходного процесса при уменьшении сопротивления R.

2.7. Метод переменных состояния

Мгновенные значения токов и напряжения, определяющие энергетическое состояние электрической цепи, называются в данном методе переменными, а сам метод назван методом переменных состояния.

Этот метод основан на составлении системы дифференциальных уравнений и, как правило, численном их решении с помощью ЭВМ.

В качестве неизвестных здесь следует принимать переменные, которые не имеют разрывов, т. е. за время t 0 не должно быть скачкообразного изменения этих величин. Такими переменными, следовательно, должны быть ток i и потокосцепление L в индуктивности, напряжение uC и заряд qC на емкости.

В противном случае при численном решении производных в точках, где имеется разрыв, возникает бесконечно большая величина, что недопустимо.

Существуют различные численные методы расчета дифференциальных уравнений. Это методы Эйлера, Рунге-Кутта и другие, которые отличаются друг от друга точностью расчета, объемом и временем вычислений. При этом, чем больше точность вычислений, тем больше требуется времени на решение.

Расчет методом переменных состояния рекомендуется вести в следующей последовательности:

1.Определить начальные условия.

2.Составить систему дифференциальных уравнений.

3.Все переменные в уравнениях п.2 выразить через токи iL или потокос-

цепления L в индуктивностях и напряжения uC или заряды qC на емкостях.

4.Все уравнения п.3 свести к нормальной форме Коши.

5.Используя стандартную программу, решить на ЭВМ уравнения п.4.

В тех случаях, когда процесс в цепи отображен дифференциальным урав-

нением n-го порядка, например
	d ni	L		an 1	d n 1i	L	...a0iL	f (t),
	dt n				dt n 1

то уравнение должно быть приведено к системе из n – дифференциальных уравнений первого порядка, записанных в нормальной форме Коши.

Для этого введем обозначения:

y

0

i

L

;

y

di

L

,...;

y

n 1

d n 1i

L

.

1

dt

dt n 1

При использовании новых обозначений получаем систему из n уравнений, записанных в нормальной форме Коши:

dy0

y ;

dt

1

dy1

y2 ;

dt

...

dyn

f (t) a

0

y

0

a y ... a

n 1

y

n 1

.

1 1

dt

Эта система может быть решена численным методом.

Тесты для самопроверки

1. Цепь, представленнаянарисунке, отключается от
источникапостоянногонапряженияU.	U
Требуется указать характеризменениятокаi (t) виндуктивности

впереходном процессе.

а

б

в

г

2. Последовательная цепь R L имеет параметры.: R =100 Ом, L = 100 мГн. Чему равнапостояннаявремениэтойцепи?

а. 1 с.

б. 10 – 3 с. в. 1с.

г. 1·10 – 4 с.

3. Цепь, представленнаянарисунке, отключается от источникапостоянногонапряженияU.

Требуется указать характеризменениятокаi (t) вемкости впереходном процессе.

а.

б.

в.

г.

4. Последовательная цепь R Симеет параметрыR =10 Ом, С = 100 мкФ. Чему

равна постояннаявремениэтойцепи?

а. 4 с. б. 10 – 3 с. в. 1 с. г. 1·10 – 2 с.

5. Какое условие необходимо для получения апериодического процесса в последовательной цепи, содержащей элементы R,L,C.

а. R 2 CL . б. R = 2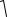 CL . в. R < 2 CL . г R << 2 CL .

6. Переходный процесс в последовательной цепи, содержащей элементы R,L,C, описывается дифференциальным уравнением какого порядка?

а. Первого порядка. б. Второго порядка. в. Третьего порядка. г. Четвертого порядка.

7. Вынужденный (установившийся) ток в цепи определяют:

а. До коммутации в момент времени, непосредственно предшествующий моменту коммутации.

б. После коммутации в момент времени, непосредственно следующий за моментом коммутации.

в. После коммутации для времени, стремящегося к бесконечности.

г. Для ответа на вопрос недостаточно данных.

8. Начальные условия используют при расчете переходных процессов. а. Для определения принужденной составляющей процесса.

б. Для определения постоянной времени цепи.

в. Для определения постоянной интегрирования при решении дифференциального уравнения.

г. Для составления дифференциального уравнения.

9. Цепь R L C подключается к источнику постоянного напряжения. Переходный процесс при R 2 CL для тока i будет…

R iL

U

L

UC

С

а. Апериодический. б. Колебательный. в. Монотонно возрастающий. г. Монотонно убывающий.

10.

В переходном процессе напряжение на емкости

uC изменяется согласно

выражению.

R

С

iC

uC Ue

t

а.

RC .

uC

t

U

R

б. uC U Ue RC .

t

в. uC U Ue RC .

t

г. uC Ue RC .

11. Постоянная времени τ переходного процесса при R=2 Ом, С=10 мкФ равна…

а. 20 с.	U			R
б. 0,2 с.

С

в. 20 мкс. г. 5 мкс.

12. Какие две величины могут быть использованы в качестве неизвестных в методе переменных состояния? Укажите правильное сочетание.

а. Ток в индуктивности и напряжение на емкости. б. Ток в сопротивлении и напряжение на емкости. в. Ток в индуктивности и ток в емкости.

г. Напряжение на индуктивности и напряжение на емкости.

ГЛАВА 6. ОПЕРАТОРНЫЙ МЕТОД РАСЧЁТА ПЕРЕХОДНЫХ ПРОЦЕССОВ В ЛИНЕЙНЫХ ЦЕПЯХ

6.1. Основы операторного метода

Цель и идея метода. Основной целью операторного метода в приложении к электротехнике является облегчение расчетов переходных процессов в электрических цепях путем упрощения решения дифференциальных уравнений, описывающих эти процессы. Последнее достигается заменой операций над реальными физическими величинами, являющимися функциями времени, операциями над их изображениями, представляющими собой искусственно подобранные функции другой по природе переменной, определенным образом связанные с оригиналами, то есть с исходными физическими величинами. При этом за счет особого подбора функциональных связей между изображениями и оригиналами удается от линейных дифференциальных уравнений для оригиналов перейти к линейным алгебраическим уравнениям для изображений. Именно это и приводит в большинстве случаев к существенному упрощению решения задачи.

Простейшие аналоги операторного метода. Напомним, что для упро-

щения расчетов мы и ранее неоднократно обращались к приемам, аналогичным операторному методу, то есть к идее оперированию с одними величинами (изображениями) вместо других (оригиналов).

Например, еще в средней школе мы встретились с приемом возведения в степень или извлечения корня с помощью логарифмирования, которое позволяло от относительно сложных операций над исходными числами перейти к более простым операциям умножения или деления их логарифмов. В этих задачах исходные числа можно рассматривать как оригиналы, а их логарифмы принять за изображения этих чисел.

В начале настоящего пособия мы познакомились с изображениями синусоидальных функций вращающимися векторами, что дало возможность заменить громоздкие операции аналитического сложения и вычитания синусоидальных функций времени оригиналов весьма простыми операциями геометрического сложения и вычитания векторов (их изображений).

Позже (ТОЭ. Ч. 1) мы перешли к изображениям синусоидальных функций комплексными функциями, что позволило еще больше упростить расчеты цепей переменного тока, благодаря тому что операции дифференцирования и интегрирования синусоидальных функций превращались в этом методе в алгебраические операции умножения и деления изображений функций (комплексных токов и напряжений) на постоянное число j .

Этапы расчета цепи. Во всех упомянутых примерах решение задачи складывалось из трех этапов:

1.Нахождение изображений заданных величин (определение логарифмов, построение векторов, запись условия задачи в комплексной форме);

2.Собственно расчеты, заключающиеся в математических операциях с изображениями (с логарифмами, векторами, комплексными числами);

3.Отыскание оригинала ответа (определение числа по логарифму, запись синусоидальной функции по построенному вектору, вычисления действующих токов по их комплексным значениям).

Аналогично по форме строится решение задачи и с применением операторного метода. Однако в последнем случае первый и третий этапы решения задачи, то есть запись изображения по оригиналу, заданному в условии задачи,

иособенно нахождение оригинала ответа по его изображению, вычисленному во втором этапе расчета, оказывается по содержанию сложнее, чем в упомянутых выше аналогиях. Это объясняется тем, что в операторном методе, который преследует цель упростить операции дифференцирования и интегрирования для всех практически встречающихся классов функций, функциональная связь между оригиналом и изображением оказывается более сложной.

Переход от оригинала к изображению. Из курса математики известно,

что переход от оригинала f t , являющегося действительной функцией време-

ни t , к его изображению F p в операторном методе обычно совершается с помощью интеграла Лапласа

F p f t exp pt d t ,

0

где аргумент p новой функции, называемый оператором, представляет собой в общем случае комплексную величину, имеющую размерность, обратную времени (l/c = c 1 ). Размерность же изображения F p , как следует из анализа интеграла Лапласа, равна размерности оригинала f t , умноженной на время (множитель exp pt в подынтегральном выражении безразмерен).

Для того чтобы приведенное преобразование, часто называемое прямым преобразованием Лапласа, стало возможным, то есть интеграл Лапласа имел конечное значение, необходимо, чтобы функция f t удовлетворяла условиям

Дирихле и возрастала по абсолютной величине не быстрее показательной функции, то есть удовлетворяла условию f t A exp t , где A и – неко-

торые положительные числа. Поскольку все реальные токи и напряжения удовлетворяют этим условиям, их изображения существуют во всех без исключения случаях.

Эквивалентность равенств оригиналов и изображений. Особо под-

черкнем, что преобразование Лапласа для данного оригинала приводит к единственному значению изображения. А это значит, что равным друг другу оригиналам будут соответствовать и равные изображения. Иначе говоря, от равенства оригиналов можно переходить к равенству их изображений.

О линейности преобразования Лапласа. Вспоминая два правила интег-

рирования, а именно: 1) постоянный множитель можно выносить за знак интеграла; 2) интеграл суммы функций равен сумме интегралов от отдельных слагаемых – нетрудно прийти к так называемому свойству линейности преобразования Лапласа, которое удобно сформулировать в виде двух раздельных правил, аналогичных правилам интегрирования:

1)изображение произведения функции на постоянную величину равно изображению функции, умноженному на ту же величину;

2)изображение суммы функций равно сумме изображений отдельных слагаемых.

Практические приемы нахождения изображений. В практике решения дифференциальных уравнений для нахождения изображений обычно не прибегают к вычислению интеграла Лапласа, а пользуются готовыми таблицами соответствий оригиналов и изображений. Приводим пример такой таблицы для наиболее часто встречающихся в электротехнике функций (табл. 6.1). В совокупности со свойством линейности преобразования Лапласа эта таблица позво-

ляет решить практически все задачи о расчете переходных процессов в электрических цепях.

Изображения производной и интеграла. Если функция f t имеет изо-

бражение F p , то, как доказывается в курсе математики, изображение производной f t представляется в виде

pF p f 0 ,

(6.1)

то есть равно изображению самой функции, умноженному на оператор р, за вычетом оригинала при нулевом значении аргумента.

В частном случае при нулевом начальном условии, то есть когда функция f t в начальный момент времени равна нулю f t 0 , изображение ее производной упрощается

pF p

(6.2)

и равно изображению самой функции, умноженному на оператор р.

Таблица 6.1

	Соотношения оригиналов и изображений
№ п/п	Оригинал	Изображение
1	A	A / p
2	Е/t	1/ p 2
3	exp t	1/ p
4	exp t	1/ p
5	1 exp t	/ p p
6	sin t	/ p2	2
7	cos t	p / p2	2
8	sin ( t )	p sin cos / p2		2
9	cos( t )	p cos sin / p2		2
10	exp t sin t	/ p 2 2
11	exp t cos t	( p ) / p 2 2
12	t exp t	1/ p 2

t	f t d t некоторой функции				f t , взятого в
Изображение интеграла
0
пределах от 0 до t, имеет вид		F p
				,	(6.3)
		p

то есть равно изображению самой функции, деленному на оператор p .

Таким образом, при переходе от оригиналов к изображениям операция дифференцирования превращается в операцию умножения, а операция интегрирования заменяется операцией деления.

О преобразовании по Карсону-Хевисайду. Наряду с разобранным выше преобразованием по Лапласу в электротехнике для связи изображений с оригиналами нередко обращаются к преобразованию по Карсону-Хевисайду, имеющему вид

Ф p p f t exp pt d t p F p

0

и отличающемуся от преобразования по Лапласу нормирующим множителем р. Таким образом, для нахождения изображения по Карсону-Хевисайду можно пользоваться приведенной таблицей при условии, что все выражения в правой колонке будут умножены на оператор р. В частности, изображением по-

стоянной величины в этом случае будет сама постоянная.

Достоинством преобразования по Карсону-Хевисайду является совпадение по размерности оригинала и изображения, в то время как преобразование по Лапласу изменяет размерность изображения по сравнению с оригиналом.

Преимуществом преобразования по Лапласу является его соответствие с преобразованием Фурье, на котором основывается еще один, так называемый частотный метод анализа цепей, получающий в настоящее время сравнительно широкое применение. Исходя из последнего соображения, а также ввиду преимущественного распространения в современной литературе преобразования по Лапласу, в настоящем пособии мы избрали именно это преобразование.

Переход от изображения к оригиналу можно осуществить, пользуясь обратным преобразованием Лапласа, которое мы здесь ке приводим, так как практически для отыскания оригиналов по заданным изображениям пользуются упомянутыми выше (табл. 5.1) таблицами соответствия оригиналов и изображений, имеющимися во всех справочниках по операторному исчислению и в

специальных пособиях по анализу переходных процессов в электрических цепях.

В тех случаях, когда изображение представляет собой отношение двух многочленов, для нахождения оригинала применяют теорему разложения.

Теорема разложения. Пусть изображение представляет собой отношение двух многочленов:

F p HG pp ,

причем степень m многочлена G p в числителе меньше степени n многочлена H p в знаменателе. Если уравнение H p 0 не имеет кратных корней и не имеет корней, равных корням уравнения G p 0 , то рассматриваемую дробь можно разложить на простейшие дроби:

G p

A1

A2

An

n

Ak

...

,

H p

p p

p p

2

p p

n

p p

1

1

k

где p1, p2 ,..., pn - корни уравнения H p 0 , обычно называемые нулями знаменателя H p , или полюсами функции F(p). Для определения коэффициентов Ak воспользуемся следующим приемом.

Умножим обе части последнего равенства на p pk и положим p pk . При этом в правой части равенства останется одно слагаемое, равное коэффициенту Ak (все остальные слагаемые обратятся в ноль), и, следовательно, для этого коэффициента имеем

Ak G pHpp pk p pk .

Так как многочлен H p при p pk обращается в ноль, то полученное

выражение представляет собой неопределенность вида 0/0. Раскрывая ее по правилу Лапиталя, получим

A	G p		lim	p pk		G pk	.
k		k		H p		H pk

p pk

Тогда в целом для всей дроби можно написать:

F p	G p n		A	n G p			1
		1	k	1	k			.
	H p		p pk		H pk		p pk

Принимая во внимание, что преобразование Лапласа обладает свойством линейности и что оригиналом дроби 1/ p pk является функция exp pk t , оригинал, соответствующий изображению F(p), получим в виде

	n	G pk
	f t			exp pk t .	(6.4)
		H pk
	1

Это равенство и называют теоремой разложения.

6.2. Применение операторного метода к расчёту переходных процессов в электрических цепях

Два возможных приема использования операторного метода Расчет переходных процессов в электрических цепях с помощью операторного метода можно построить двумя путями.

Впервом случае:

1)Для рассматриваемой цепи, используя законы Кирхгофа, составляют необходимые уравнения с мгновенными токами и напряжениями. Далее от этих уравнений, являющихся линейными интегродифференциальными уравнениями, переходят к соответствующим алгебраическим уравнениям относительно операторных изображений:

ft F p .

2)Находятся операторные изображения искомых величин (токов и напряже-

ний).

3) По таблицам или с использованием теоремы разложения определяются искомые величины (сами токи и напряжения).

Во втором случае:

1)Задана схема и параметры цепи.

2)Стадию составления уравнения с мгновенными значениями опускают, при-

влекая операторную форму с самого начала анализа конкретной цепи. Для этого рассчитываются независимые начальные условия iL 0 и uC 0 в схеме до

коммутации.

3) Составляется операторная схема замещения.

Этот подход, являющийся с практической точки зрения более удобным, требует для своей реализации знания некоторых дополнительных понятий, знакомству с которыми и посвящен настоящий параграф.

Независимо от избранного приема расчета электрических цепей с помощью операторного метода следует иметь в виду, что при отыскании изображе-

ния с помощью интеграла Лапласа интегрирование оригинальной функции по времени производится от нуля. Иными словами, на изображении не скажутся значения этой функции до момента t = 0. Поэтому при решении задач операторным методом момент t = 0, то есть начало исследования переходного процесса следует выбирать так, чтобы все ранее происходившие в цепи процессы и характеризующие их величины нам были точно известны.

Законы Кирхгофа в операторной форме. Принимая во внимание свойст-

ва единственности и линейности преобразования Лапласа, нетрудно прийти к заключению, что оба закона Кирхгофа, записанные в свернутой форме для мгновенных токов в ветвях узла и напряжений на элементах контура

ik 0, uk 0 ,

могут быть переписаны в аналогичной форме для изображений соответствующих величин:

Ik p 0 ,	(6.5)
Uk p 0 ,	(6.6)

где Ik p – изображение тока ik , называемое операторным током k -й ветви; Uk p – изображение напряжения uk , называемое операторным напряжением

на k -м элементе цепи.

Последние уравнения, получившие названия уравнений Кирхгофа в операторной форме, формулируются следующим образом:

1)Алгебраическая сумма операторных токов в расходящихся из узла ветвях равна нулю (первый закон Кирхгофа).

2)Алгебраическая сумма операторных напряжений на элементах замкнутого контура равна нулю (второй закон Кирхгофа).

При этом следует иметь в виду, что операторные напряжения и токи данного элемента цепи в общем случае связаны друг с другом иными зависимостями, чем действительные мгновенные значения этих величин. Рассмотрим эти связи.

Операторное напряжение на резисторе. Мгновенные напряжение uR и

ток i идеального резистора с сопротивлением R связаны между собой законом Ома:

uR Ri .

Переходя в этом уравнении от действительных величин напряжения и тока к их изображениям, то есть к операторным напряжению и току, с учетом свойства линейности преобразования Лапласа получим

U R p R I p . (6.7)

Таким образом, операторное напряжение U p на идеальном резисторе связано с операторным током I p в нем тем же коэффициентом R , которым

связаны оригиналы этих величин в обычном законе Ома. Тем не менее в последнем уравнении, называемом иногда законом Ома в операторной форме, коэффициент R принято именовать операторным сопротивлением резистора, хотя, по существу, оно не отличается от обычного понятия электрического сопротивления резистора.

Операторное напряжение на катушке. Мгновенные напряжение uL и

ток i идеальной катушки с индуктивностью L связаны друг с другом законом электромагнитной индукции:

uL L	d i	.
	d t
Принимая во внимание правило изображения производной, это уравнение
в операторной форме можно записать в виде
U L p L p I p i 0 ,
где i 0 — ток катушки в начальный момент времени.
Раскрывая скобки в правой части последнего равенства, имеем
U L p L p I p Li 0 .			(6.8)
В частном случае нулевого начального условия i 0 0			выражение для
операторного напряжения упрощается:
U L p L p I p			(6.9)

и по форме совпадает с законом Ома, если, как это обычно принято, рассматривать произведение pL в качестве операторного сопротивления катушки.

Операторное напряжение на конденсаторе. Мгновенный ток i идеаль-

ного конденсатора выражается через мгновенное напряжение uC на нем в виде i C ddutC .

Переходя к операторной форме записи этого уравнения, получим

I p C pUC p uC 0 ,

где uC 0 - напряжение на конденсаторе в начальный момент времени.

Отсюда нетрудно получить выражение для операторного напряжения на идеальном конденсаторе

UC p	1	I p	uC 0	.	(6.10)
	pC
			p

В частном случае нулевого начального условия uC 0 0 последнее выражение упрощается и приобретает форму закона Ома при условии, если дробь 1/ pC принять за операторное сопротивление конденсатора.

Операторные схемы. Пользуясь вышеприведенными выражениями для операторных напряжений на идеальных резисторе, катушке и конденсаторе, можно для любой цепи составить уравнения по законам Кирхгофа непосредственно в операторной форме. При этом, как и в случае обычных приемов расчета цепи, на схеме следует пометить положительные направления искомых и заданных величин, в данном случае операторных токов в отдельных ветвях схемы и операторных напряжений на ее элементах. Операторные ЭДС источников энергии направляются в соответствии с заданными положительными направлениями их действительных ЭДС.

Составление операторных уравнений упрощается, если взамен обычной схемы вычертить операторную схему цепи, отличающуюся от первой добавлением к катушкам и конденсаторам идеальных источников энергии.

Действительно, возвращаясь к выражениям операторных напряжений на катушке и конденсаторе

U L p L p I p Li 0 ,

UC p pC1 I p uCp0 ,

полученным ранее, представим вторые слагаемые L i 0 и uC 0 / p в правых

частях написанных уравнений как операторные ЭДС идеальных источников напряжения, включенных последовательно с катушкой и конденсатором (рис. 5.1). Катушку и конденсатор на этих схемах следует считать пассивными элементами с операторными сопротивлениями pL и 1/ pC .

Рис. 6.1. Операторные напряжения на катушке и на конденсаторе

При этом операторную ЭДС L i 0 источника, отражающего начальный ток катушки, следует направить в ту же сторону, куда направлен ее операторный ток I p (рис. 6.1, а), а операторную ЭДС uC 0 / p источника, воспроизводящего начальное напряжение конденсатора, - навстречу его операторному напряжению U C p (рис. 6.1, б). В справедливости последних оговорок легко

убедиться, составив по указанным на рис. 6.1 контурам уравнения по второму закону Кирхгофа, полагая операторные сопротивления катушки и конденсатора равными соответственно pL и 1/ pC :

U L p pL I p Li 0 ,

	UC p	1	I p uC 0 .
		pC
			p

Как видно, составленные уравнения совпадают с приведенными выше выражениями для операторных напряжений на катушке и конденсаторе.

На рис. 5.2, б в качестве примера приведена операторная схема, соответствующая обычной схеме цепи с идеальными элементами (рис. 6.2, а). Около каждого пассивного элемента операторной схемы для наглядности подписывают его операторное сопротивление, а у каждого источника указывают его операторную ЭДС.

Очевидно, что при нулевых начальных условиях операторная схема упрощается за счет выпадения искусственно вводимых источников.

Следует подчеркнуть, что операторные схемы должны соответствовать тому состоянию цепи, в которой исследуется происходящий переходный процесс.

а)

Рис. 6.2. Примеры электрической схемы (а), представленной в операторной форме (б)

Операторная схема индуктивно связанных катушек. Рассмотрим две индуктивно связанные катушки с индуктивностями Lk и Lm и взаимной индук-

тивностью М (рис. 6.3, а).
При указанных на схеме направлениях токов ik								и im в этих катушках и
приведенной разметке их выводов напряжения на катушке будут равны
u		L d ik	M d im ;	u		L	d im M d ik .
	k	k d t	d t		m	m d t		d t

Рис. 6.3. Операторные схемы (б) двух индуктивно связанных катушек (а) Переходя к операторной форме записи этих выражений, получим

Uk p pLk Ik p pMIm p Lk ik 0 Mim 0 ,

Um p pLm Im p pMIk p Lmim 0 Mik 0 ,

и, следовательно, в общем случае на операторной схеме двух индуктивно связанных катушек последовательно с каждой из них следует включить по два идеальных источника напряжения с операторными ЭДС, указанными на рис. 5.3, б.

В частном случае нулевых начальных условий для токов катушек эта схема существенно упрощается, так как из нее исключаются искусственно введенные источники.

Эквивалентные операторные сопротивления и проводимости Пред-

ставим себе участок электрической цепи без источников энергии. При нулевых начальных условиях (токи в катушках и напряжения на конденсаторах в начальный момент равны нулю) операторная схема такого участка не будет содержать искусственно вводимых операторных ЭДС. Поэтому связь между опе-

раторными напряжением U p и током I p на этом участке цепи будет опре-

деляться только параметрами его резисторов, катушек и конденсаторов. В этих условиях отношение операторного напряжения к операторному току

	Z p	U p		(6.11)
		I p

называют эквивалентным операторным сопротивлением участка. Например, для цепи с последовательным соединением идеальных резистора R , катушки L и конденсатора С (рис. 6.4, а) операторная схема при нулевых начальных условиях будет выглядеть, как показано на рис. 6.4, б. Поэтому для ее операторного напряжения можно написать:

	U p U R p U L p UC p RI p pLI p					1	I p ,
						pC
	откуда для эквивалентного операторного сопротивления получим
	Z p	U p	R pL	1	,
		I p		pC

то есть эквивалентное операторное сопротивление рассматриваемой цепи равно сумме операторных сопротивлений резистора, катушки и конденсатора.

Обобщая этот результат, нетрудно прийти к выводу, что эквивалентное операторное сопротивление группы n последовательно соединенных элементов равно сумме операторных сопротивлений отдельных элементов этой группы:

Z p Z1 p Z2 p ... Zn p .			(6.12)
Отношение операторного тока к операторному напряжению участка цепи
при нулевых начальных условиях
Y p	I p		(6.13)
U p

называют эквивалентной операторной проводимостью участка. Например, для цепи с параллельным соединением идеальных резистора R , катушки L и конденсатора С (рис. 6.5, а) операторные схемы при нулевых начальных условиях изобразятся в виде, представленном на рис. 6.5, б.

Рис. 6.4. Схемы последовательно включённых R, L, C

Поэтому для операторного тока в неразветвленной части схемы можно написать:

I p IR p IL p IC p U p U p

U p

,

R

pL

1

pC

откуда для эквивалентной операторной проводимости получим

Y p

I p

1

1

pC .

pL

U p

R

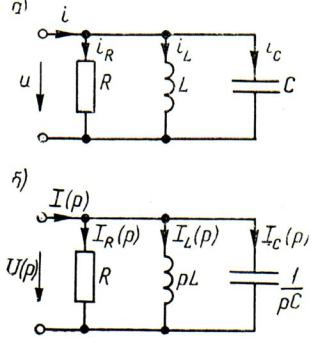
Рис. 6.5. Схемы параллельно включённых R, L, C

Принимая величины 1/ R G , 1/ pL и pC соответственно за оператор-

ные проводимости резистора, катушки и конденсатора, получим, что эквивалентная операторная проводимость рассматриваемой цепи (рис. 6.5, а) равна сумме операторных проводимостей ее элементов.

Обобщая этот результат, нетрудно прийти к выводу, что эквивалентная операторная проводимость группы n параллельно соединенных элементов равна сумме операторных проводимостей отдельных элементов этой группы:

Y p Y1 p Y2 p ... Yn p .

(6.14)

Таким образом, приемы расчета эквивалентных операторных сопротивлениях и проводимостей при последовательном и параллельном соединении элементов цепи полностью совпадают с приемами аналогичных вычислений в цепях постоянного тока.

Принимая во внимание, что эквивалентные операторные сопротивление и проводимость обратны друг другу:

	Y p	1		,	(6.15)
		Z p

что непосредственно следует из сопоставления выражений (5.11) и (5.13), становится очевидным, что сформулированное выше заключение можно распро-

странить и на случай смешанного соединения элементов. Например, эквивалентное операторное сопротивление цепи, показанной на рис. 6.6, будет равно

RL

pL

1

Z p R

pC

.

RL pL

1

pC

При указанных на схеме направлениях токов ik и im

в этих катушках и

приведенной разметке их выводов напряжения на катушке будут равны

u

L d ik

M d im

; u

L

d im M d ik .

k

k d t

d t

m

m d t

d t

Рис. 6.6. Схема смешанного соединения элементов R, L, C

В заключение заметим, что понятия об эквивалентных операторных сопротивлениях и проводимостях при сохранении приемов их расчета через параметры элементов электрических цепей распространяются на цепи при любых начальных условиях. Однако при ненулевых начальных условиях теряют силу приведённые выше соотношения (6.11) и (6.13), представляющие собой закон Ома в операторной форме.

6.3. Простейшие примеры расчёта переходных процессов

Разрядка конденсатора на резистор. В качестве про стейшего примера применения операторного метода к расчету переходных процессов рассмотрим ранее рассмотренную классическим способом задачу о разрядке конденсатора на идеальный резистор (рис. 6.7, а). Как и прежде, начальное напряжение на конденсаторе примем равным uC 0 UC0 .

В соответствии с этим начальным условием операторная схема для рассматриваемой цепи будет выглядеть, как показано на рис. 5.7, б. Поэтому операторное уравнение, записанное по второму закону Кирхгофа, представится в виде

1

U

R

I p

C0 ,

pC

p

откуда

UC0

UC0

1

I p

.

1

1

R

p

p R

RC

pC

Согласно табл. 6.1, и свойству линейности преобразования Лапласа полученному изображению тока будет соответствовать оригинал (позиция 3 табли-

цы 6.1)

i t	U		C0						t
					exp
								RC
		R
или, вводя обозначение для постоянной времени RC ,
i t		U		C0					t
						exp					,
			R

что соответствует результату, полученному ранее при решении этой задачи классическим методом.

Для напряжения на конденсаторе имеем

UC p

1

I

p uC 0 UC0

1

UC0

1

pC

p

pRC p

p

RC

UC0

1

1

UC0

.

1

p

1

1

p

RC p

RC

RC

По табл. 6.1 находим оригинал (позиция 3):

t

t

uC t UC0 exp

UC0 exp

,

RC

что также соответствует ранее полученному ответу (выражение ).

Рис. 6.7. Схемы разрядки конденсатора на идеальный резистор

Включение реальной катушки под постоянное напряжение. Посколь-

ку в этой задаче (рис. 6.8) мы встречаемся с нулевым начальным условием i 0 0 (ток в катушке до замыкания ключа, естественно, отсутствует), операторная схема цепи не будет отличаться от ее обычной схемы и обращаться к ней смысла нет. Операторный ток здесь можно выразить по закону Ома:

I p UZ pp ,

Рис. 6.8. Схема включения реальной катушки под постоянное напряжение

причем для операторного сопротивления такой цепи, принимая во внимание, что катушка помимо индуктивности обладает также и сопротивлением R , имеем

Z p R pL .

Так как изображение U p питающего напряжения, являющегося постоянной величиной U , равно

U p Up ,

операторный ток представится в виде
I p	U
		.
	p R pL

Для нахождения оригинала, соответствующего полученному изображению тока, применим теорему разложения, представив изображение тока в виде дроби:

I p HG pp ,

где G p U , а H p p R pL .

Так как корни знаменателя будут p1 0 , p2 R / L , а производная знаменателя равна H p R 2 pL , то, согласно теореме разложения получим

i t

G p

k

exp pk t

U

U

R

U

R

exp

t

1

exp

t .

H pk

R

R

L

L

R

R

2 L L

Вводя обозначение постоянной времени L / R , окончательно получим

i t

U

t

1 exp

,

R

что совпадает с ответом для аналогичной задачи, решенной ранее классическим методом (формула ).

Заметим, что полученное выше выражение для изображения тока легко

преобразовать к табличной форме:
	U		U			U	R
I p							L
						R			,
	p R pL			R				R
			Lp p				p p
				L				L

позволяющей сразу записать полученное выше выражение для тока (см. позицию 4 в табл. 6.1).

Включение смешанной емкостной цепи под постоянное напряжение.

В качестве нового примера расчета переходного процесса операторным методом рассмотрим процесс включения смешанной цепи с конденсатором С и двумя резисторами R1 , R2 (рис. 6.9, а) под действием постоянного напряжения U.

Полагая, что конденсатор до включения цепи был разряжен, то есть принимая

нулевое начальное условие uC 0 0 , можно, как и в предыдущем примере, на-

писать выражение для операторного тока в неразветвленной части цепи, не обращаясь к операторной схеме цепи:

	U p				U
I p					p
	Z p				R2			1
				R1			pC
					R			1
				2				pC

и учитывая, что изображение U p постоянного напряжения U представляет собой величину U / p (табл. 6.1), а операторное сопротивление Z p цепи определяется способом соединения ее элементов (резистор R1 включен последовательно с группой параллельно соединенных конденсатора С и резистора R2 ).

Выполняя несложные алгебраические преобразования дроби, выражение для операторного тока I1 p можно преобразовать к виду

R2

1

1

1

pC

pR1R2C

I1 p U

U

R1

R1 R2

p R R

p R1 R2

1

2

pC

R1R2C

R1 R2

U

1

U

R1R2C

,

R

R R

R R

R1

R2

1

p

1

2

1

2

R1R2C

p p

R R C

1

2

удобному для отыскания оригинала по табл. 6.1. Действительно, вводя обозначение

R1R2 C , R1 R2

для операторного тока получим
		U	1				U		1
I1	p												,
		R	p	1		R		R			1
		1				1		2		p p

чему соответствует ток переходного процесса (позиции 3 и 4 в табл. 5.1)

i

f

t

U

t

U

t

f

t f

t .

exp

1

exp

R

R

R

1

1

C

2

1

1

2

Таким образом, ток i1 в неразветвленной части цепи при переходном про-

цессе выражается суммой двух экспоненциальных функций с постоянной времени , построенных на рис. 6.9, б, то есть изменяется также по экспоненте от начального значения U / R1 до установившейся величины U R1 R2 .

Нетрудно показать, что составляющие fC t и f2 t этого тока являются соответственно токами iC и i2 переходного процесса в конденсаторе и резисторе R2 . В самом деле, операторный ток конденсатора при нулевых начальных условиях можно представить в виде

					1
IC p UC p				R2						.
			pCI1 p			pC
1				R			1
	pC			2			pC

Подставляя сюда первое из записанных выражений для I1 p , имеем

																R2				1
IC p pC	U		1																pC											UR
																															2
	p			R2				1								R2				1											R R
																											p R R					1 2
								pC												pC
																													1 2			pC
		R1
				R	2				1
									pC
			U								1										U						1			,
			R			p					R1				R2						R					p		1
			1																		1
											R R C
											1				2

откуда для оригинала iC тока конденсатора получим

i		U			t		f		t .
		R	exp
C								C
		1

Принимая во внимание очевидное соотношение i1 iC i2 ,

приходим к выводу, что второе слагаемое, действительно, является током второго резистора:

i		f		t		U					t
								1	exp				.
					R	R
	2		2
					1		2

Очевидно, что напряжение uC на конденсаторе, равное напряжению на резисторе R2 , при переходном процессе будет изменяться аналогично току i2 :

u		u		R i				UR	2				t
										1	exp					,
								R	R
	C		2		2	2
то есть кривая f2 t на рис. 6.9,								1	2
					б в измененном масштабе может рассматри-

ваться как кривая напряжения uC на конденсаторе.

6.4. Включение цепи RLC под постоянное напряжение

Формулировка задачи. В качестве более сложного примера расчета переходного процесса операторным методом рассмотрим включение цепи RLC (рис. 6.10) под постоянное напряжение U , полагая, что конденсатор перед включением цепи был разряжен. Начальными условиями в этом случае будут равенства нулю тока в цепи и напряжения на конденсаторе:

i 0 0 ,

uC 0 0 .

Рис. 6.9. Схемы включения смешанной емкостной цепи под постоянное напряжение

Z p R

I p

R

Подчеркнем, что предлагаемый пример представляет собой не только теоретический, но и большой практический интерес. В частности, он соответствует важной реальной задаче зарядки конденсатора от постоянного напряжения, когда даже при отсутствии специально включенных резистора и катушки приходится считаться с активным сопротивлением и индуктивностью соединительных проводов.

Рис. 6.10. Включение цепи RLC под постоянное напряжение

Ток переходного процесса. Нулевые начальные условия позволяют вос-

пользоваться в этой задаче законом Ома в операторной форме:

I p UZ pp ,

найти операторный ток по операторному сопротивлению цепи:

pC pC1

в виде

U p pL pC1

или, принимая во внимание, что изображением постоянного напряжения U является функция U/p, оригинал тока, соответствующий этому изображению, будем искать по теореме разложения, для чего сначала определим нули знаменателя, то есть корни уравнения:

p2 RL p LC1 0,

являющегося характеристическим уравнением для рассматриваемой цепи. Используя сокращенные обозначения

R

и

0

1

,

2L

LC

для двух неравных при 0 корней этого уравнения получим

p

R

R

2

1

2 2 .

1,2

2L

2L

LC

0

Тогда, ориентируясь на изображение тока как на отношения двух много-

членов

U

G p

I p

L

p2

R p

1

H p

LC

L

и производную знаменателя

R

2 p ,

H

p 2 p L

оригинал тока (действительный ток цепи) получим в виде

i t

G pk

exp pk t U

1

exp p1t U

1

exp p2t

H pk

L 2 p1

L 2 p2

U

exp p t

exp p

t

1

2

L

2

2

2

2

2

2

0

0

U

exp p1t exp p2t .

2L

2

02

Напряжение на конденсаторе. Для операторного напряжения на кон-

денсаторе при начальном условии uC 0 0 можно написать:

G p

UC p I p

1

U

1

.

pC

LC

2

R

1

H p

p p

p

L

LC

Знаменатель этой функции, наряду с полученными выше корнями p1,2 2 02

многочлена в знаменателе, взятого в скобках, будет иметь и третий корень: p3 0 .

Поскольку производная от знаменателя на этот раз представится в виде

H p 3p2 2 RL p LC1 3p2 4 p 02 ,

её частные значения будут равны

H p1 3 2 02 2 4 2 02 022 2 02 2 02 2 2 02 p1 .

H p2 3 2 02 2 4 2 02 02

2 2 02 2 02 2 2 02 p2 , H p3 02 LC1 ,

и согласно теореме разложения для напряжения на конденсаторе получим

uC t

G pk

exp pk t

U

1

exp p1t

LC 2 2 02 p1

H pk

U

1

exp p2t

U

1

.

LC 2 2 02 p2

LC

1

LC

Так как

p1 p2 2 02 2 02 02

1

,

LC

то, приводя первые два слагаемых к общему знаменателю, выражение для напряжения конденсатора удается несколько упростить:

u	C	t	U	p		exp p t p		exp p	t U .
			2 2 02		2	1	1	2

Характер переходного процесса определяется числовыми значениями корней и, как и в случае ранее разобранной задачи о разрядке конденсатора на цепь RL, может быть апериодическим (при вещественных корнях) или колебательным (при комплексных корнях). Остановимся на этих вариантах в отдельности, а также рассмотрим особый случай равенства корней p1 p2 , когда

применение теоремы разложения становится невозможным.

Апериодический переходный процесс в цепи RLC наступает при вещест-

венных корнях p1 и p2 , когда 0 , то есть R 2 L / C 2 .

Сравнивая выражение для тока переходного процесса в рассматриваемой задаче

	i t		U		exp p1t exp p2t
		2L	2	02

с выражением для тока, полученным ранее при анализе апериодического процесса разрядки конденсатора на цепь RL, нетрудно убедиться, что они отличаются друг от друга только знаком (показатели степени в этих выражениях одинаковы, то есть p1 1 и p2 2 . Это говорит о том, что характер зависимости

тока от времени в обеих задачах одинаков и кривая тока переходного процесса в настоящей задаче (рис. 6.11, а) будет представлять собой зеркальное изображение в оси абсцисс кривой i , построенной на рис. 5.21, в.

а)

б)

0

Рис. 6.11. Характер зависимостей переходного процесса

Кривая напряжения на конденсаторе в соответствии с полученным выше выражением

u	C	t	U	p		exp p t p		exp p	t U
			2 2 02		2	1	1	2

при вещественных отрицательных корнях p1 и p2 будет выглядеть, как показано на рис. 6.11, а. Возрастая монотонно от нуля, напряжение uC в дальнейшем асимптотически приближается к установившемуся значению, равному питающему напряжению U. При этом в момент tm , когда ток достигает максимального значения, скорость нарастания напряжения на конденсаторе также становится наибольшей (точка n перегиба кривой uC ).

Колебательный переходный процесс возникает при комплексных корнях

p1 и p2 , когда 0 , то есть R 2 L / C 2 . Представив в этом случае корни в виде

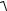p1,2 2 02 j 02 2 j ,

где

							02	2 ,
для тока в цепи можно записать:
i t	U		exp p t exp p		t		U	exp t exp j t exp j t .
	2L 2	02	1	2			j2 L
	Вспоминая формулу Эйлера
				sin exp j exp j					,
								2 j

выражающую синус через показательные функции с мнимым аргументом, предыдущее выражение нетрудно преобразовать к виду

i t UL exp t sin t .

Это выражение отличается от полученного ранее при анализе колебательного процесса разрядки конденсатора на индуктивную цепь лишь знаком и определяет собой ток, изменяющийся по затухающей синусоиде, как показано на рис. 6.11, б.

Напряжение на конденсаторе (выражение для него было получено ранее)

u	C	t	U	p		exp p t p		exp p	t U
			2 2 02		2	1	1	2

при комплексных корнях p1 и p2 также можно представить через тригонометрические функции. Для этого, раскрыв выражение в скобках

p2 exp p1t p1 exp p2t j exp j t j exp j t
			exp t exp j t exp j t j exp j t exp( j t)
и вспоминая ранее введенное обозначение							2 02		j , напряжение для uC
запишем в виде
u		t	U			exp j t exp j t		exp j t exp j t			U .
	C			exp t
						2 j			2
		Имея в виду формулы Эйлера
				sin exp j exp j , cos exp j exp j						,
						2 j			2

для напряжения на конденсаторе получим

uC t U exp t sin t cos t U

	0
U				sin t		cos t		U .
		exp t
			0		0

Нетрудно убедиться, что коэффициенты при синусе и косинусе при условии 0 можно представить как тригонометриче ские функции некоторого

угла :

	sin ;		cos ,
0
		0

что, пользуясь известной формулой тригонометрии

cos x y cos x cos y sin x sin y ,

позволяет напряжение на конденсаторе окончательно преобразовать к виду uC t U 0 exp t cos t U .

Таким образом, напряжение uC , возрастая в начале переходного процесса

от нуля (рис. 6.11, б), в дальнейшем претерпевает затухающие колебания, но не около нулевого значения, как это имело место для тока в цепи, а около установившегося значения U, к которому оно стремится при бесконечном течении времени.

Заслуживает особого внимания возникающий через полупериод от начала переходного процесса всплеск UC max напряжения на конденсаторе, превы-

шающий по величине установившееся напряжение U. Легко убедиться, что при малом затухании колебательного процесса, то есть при 0 R 0 , этот всплеск может достичь двойного установившегося значения напряжения на конденсаторе (UC max 2U ). Именно на это напряжение и приходится ориен-

тироваться при зарядке конденсатора через цепь с малым сопротивлением, чтобы не допустить пробоя его изоляции.

Граничные условия переходного процесса наступают при 0 . В этом случае оба корня p1 и p2 знаменателя в выражении для операторного тока оказываются одинаковыми:

p1,2 2 02

и применение теоремы разложения становится невозможным.

Однако в этом случае изображение тока легко преобразуется к более про-

стому виду:

I p U

1

U

1

U

1

U

1

,

R

1

L

p

2

L p2 2 p 02

L p2 2 p 2

L ( p )2

L p

LC

который позволяет найти оригинал непосредственно по табл. 6.1 (см. позицию

12).

Как было выяснено ранее, этому выражению тока в цепи соответствует апериодический процесс, качественно аналогичный изображенному на рис. 6.11, а.

6.5.Комбинированный метод расчёта переходных процессов

всложных цепях

Переходные процессы в цепях со взаимной индуктивностью. Рассмот-

рим переходный процесс в воздушном трансформаторе при U const . Уравнения после коммутации:

R i		L	d i1			M d i2			U ,
	1 1	1		d t				d t
					d i2			d i1
R2 i2		L2					M		0.
					d t			d t

Рис. 6.12. Физическая схема воздушного трансформатора Преобразуем уравнения по Лапласу:

				p p L I			p L i 0 p M I						p M i				0	U	,
R I						1						2				2		p
	1	1			1				1 1
R I			2		p p L I			2	p L i	2	0 p M I			1	p M i 0			0.
	2				2				2								1

Этой системе уравнений соответствует следующая операторная схема замещения (рис. 6.13).

Рис. 6.13. Операторная схема замещения воздушного трансформатора

Итак, взаимная индуктивность в схеме учитывается напряжением

p M Ix p M ix 0 , где ix и I x p — соответственно ток в «чужой» цепи и его

изображение. Знак напряжения определяется полярностью включения катушек. Отметим принципиально важное обстоятельство: учёт взаимоиндуктивности катушек не приводит к повышению порядка характеристического урав-

нения. В нашем случае порядок уравнения равен 2.

Комбинированный метод расчёта переходных процессов (определение свободных составляющих операторным методом). Пусть требуется рассчи-

тать следующую цепь (рис. 6.14).

Рис. 6.14. Физическая схема электрической цепи

Каждый из переходных токов электрической цепи состоит из суммы установившейся (принужденной) и свободной составляющих, например, ток

i2 t i2 уст i2св.

Принужденный (установившийся) режим можно определить отдельно. Нужно изобразить схему принужденного режима и любым методом рассчитать его, т. е. определить i1ПР,i2ПР,i3ПР .

Теперь для расчёта переходных токов остаётся определить лишь их свободные составляющие. Составим уравнения по законам Кирхгофа для свободных составляющих токов. Поскольку свободные токи вызваны энергией, запасенной в реактивных элементах цепи, то источники ЭДС (и токов) в схеме для свободного режима отсутствуют:

	i1CB		i2CB i3CB ,
	R1 i1CB R2i2CB L			d i	2CB		0,
		d i		d t		1
			2CB R3 i3CB					i3CB d t.
R2 i2CB L
						C
		dt

Перейдём к изображениям:

I1CB p I2CB p I3CB p ,

R1 I1CB p R2 I2CB p pL I2CB p i2CB 0 L 0,

6.16

R

2

I

2CB

p pL I

2CB

p L i

2CB

0 R I

3CB

p

1

I

3CB

p

3

pC

UC CB 0

0.

p

Системе (6.16) соответствует операторная схема замещения для свободных составляющих.

Значения свободных токов в индуктивности и напряжения на конденсаторе определяются как

Рис. 6.15. Физическая схема для свободных составляющих токов цепи

Рис. 6.16. Операторная схема замещения для свободных		со-
ставляющих токов цепи
iLCB 0 iL 0 iLYCT 0 ;	uC CB 0 uC 0 uCYCT 0 .

Решая уравнения (6.1), определим изображение исходного тока, а затем перейдём к оригиналу. Итоговое решение находим как сумму установившегося и свободного процессов:

i1 t i1YCT t i1CB t и т. д.

Можно сформулировать методику расчёта токов в электрической цепи при переходном процессе следующим образом:

1.Рассчитывается схема до коммутации. Цель – определение независимых начальных условий: iL t и uC t .

2.Рассчитывается установившийся режим. Цель – определение установившихся токов (напряжений) в цепи. Определение установившихся значений

токов в индуктивностях iL YCT и напряжений на ёмкостях uC YCT .

3. Определяются начальные значения свободных составляющих:

iLCB 0 iL 0 iLYCT 0 ; uC CB 0 uC 0 uCYCT 0 .

4. Составляется операторная схема замещения для свободного процесса. Это означает, что в схеме отсутствуют источники, соответствующие реальным источникам напряжения и тока, а присутствуют только источники, учитываю-

щие ненулевые значения свободных составляющих uC CB 0 и iL CB 0 .

Рис. 6.17. Операторные изображения свободных составляющих

5.Определяются изображения свободной составляющей искомой величины ICB p и оригинал iCB t .

6.Записывается общее решение:

i t iYCT t iCB t .

Отметим, что комбинированный метод проще, чем стандартный операторный метод, по той причине, что в изображение не входят источники напряжения, тока, и оно получается менее громоздким.

Пример. На рис. 6.18 приведена схема, в которой требуется определить ток i t после замыкания коммутатора.

Дано: E 10 В; R1 R2 = 100 Ом; L = 10 Гн; C = 10 мкФ.

Рис. 6.18. Расчётная схема

Решение

1. Определяем токи и напряжения на реактивных элементах в предшествующем режиме (рис. 6.19).

iL ПРЕД iL 0 0 ; uC ПРЕД E uC 0 10 В.

2. Установившийся режим после коммутации (рис. 6.20).

iL YCT i1YCT E / R1 0,1A iL YCT 0 ; uCYCT E 10 B uCYCT 0 .

Рис. 6.19. Схема предшествующего режима

Рис. 6.20. Схема установившегося режима

3. Расчёт:

iL CB 0 iL 0 iL YCT 0 0 0,1 0,1 А; uC CB 0 uC 0 uC YCT 0 10 10 0.

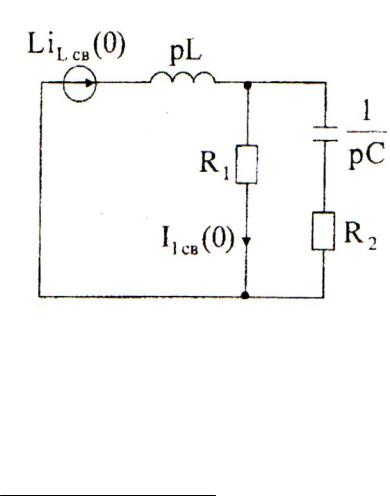
Рис. 6.21. Операторная схема для расчёта свободной составляющей тока Определение свободной составляющей тока в операторной форме:

I1CB

p LiL CB 0

R 1/ pC

p L R

p L R 1/ pC R 1/ pC R

0,1

pC R 1

0,1

10 3 p 1

2 LC R p2 p L C R2 R

2 10 3 p2 1,1 p 100

10 4 p 0,1

0,05 p 50

0,05 p 50

;

2 10 3

p2 1,1 p 100

p2

550 p 50 103

p 435 p 115

i

t 0,05 435 50 exp 435t 0,05 115 50 exp 115t

CB

435 115

115 435

0,08828exp 435t 0,1383exp 115t .

4.Итоговое решение:

i1 t iYCT iCB t 0,1_ 0,1383exp 115t 0,088exp 435t .

Тесты для самопроверки

1. Какое интегральное преобразование используется в операторном методе?

а. Интегральное преобразование Фурье; б. Интегральное преобразование Лапласа;

в. Используются оба преобразования, указанные в пунктах 1 и 2. 2. Справедливы ли законы Кирхгофа в операторной форме?

а. Нет; б. Да;

в. Справедлив только первый закон Кирхгофа;

	г. Справедлив только второй закон Кирхгофа.
3. Укажите правильный вариант законов коммутации.
а.	iL(–0) = iL(+0),	uC(–0) = uC(+0);	б. iL(–0) = uC (+0),	iL(+0)= uC(+0);
в.	iL(–0) ≠ iL(+0),	uC(–0) ≠ uC(+0);	г. iL(+0) = uC (+0),	iL(+0)= uC(–0).
4. Укажите правильный вариант			операторных сопротивлений резистора,
индуктивности и емкости.
	а. R, pL, pC;	б. R, 1/pL, pC;	в. pR, pL, pC ;	г. R, pL, 1/ pC;

5.В каких случаях в схему замещения вводят дополнительные источники?

а. При нулевых начальных условиях;

б. При начальных условиях, отличных от нулевых;

в. Во всех случаях;

г. Не достаточно данных для ответа.

6.Можно ли в операторном методе для расчета использовать метод контурных

токов и метод узловых потенциалов.

а. Нет; б. Да; в. Только метод контурных токов; г. Только метод узло-

вых потенциалов.

7. По какой формуле определяется дополнительная ЭДС в схеме замещения ем-

костного элемента при ненулевых начальных условиях?

а. EC = Ci(0); б. EC =R Ci(0); в; EC = Ci(0) /p г. EC = -uC(0) /p .

8. По какой формуле определяется дополнительная ЭДС в схеме замещения ин-

дуктивного элемента при ненулевых начальных условиях.

а. EL = Li(0); б. EL =- Li(0); в. EL = pLi(0); г. EL = Li(0)/p

9. Требуется ли вводить дополнительную ЭДС для резистивного элемента?

а. Нет; б. Да; в. Не достаточно данных для ответа.

10. Определите операторную ЭДС индуктивностиEL ( p) для цепи с парамет-

рами

U=10 B, R=5 Ом, L=0,2 Гн.

R

U	L	uL	R

iL

а. EL ( p) 0, 4 .

б. EL ( p) 2 .

в. EL ( p) 10p .

г. EL ( p) 5p .

11. Определите операторную ЭДС емкости EC ( p) для цепи с параметрами

U=10 B, R=5 Ом, С=10 мкФ.

R

а. EC

( p) 10

;

p

U

С

uC

R

б. E

( p) 10 ;

C

i

p

C

в. EC ( p) 20;

г. EC ( p) 2 .

12. Укажите операторное сопротивление z(p) для схемы.

а.

б.

в.

г.

R ( pL

1

)

pc

;

L

R pL

1

U

R

pc

С

R pL

1

;

pc

1

RpL

;

pc

pL R

R pL

1

.

pc

ГЛАВА 7. РАСЧЁТ ПЕРЕХОДНЫХ ПРОЦЕССОВ МЕТОДАМИ НАЛОЖЕНИЯ И СПЕКТРАЛЬНЫМ

7.1. Метод наложения

Интеграл Дюамеля. Расчет переходного процесса при включении линейной цепи на напряжение u t , являющееся любой функцией времени, может быть произведен методом наложения, если заменить кривую напряжения сту-

пенчатой кривой (рис. 7.1). Тогда можно считать, что в момент времени t 0

цепь включается на постоянное начальное напряжение u 0 , а затем на ряд смещенных на равные промежутки времени x постоянных напряжений u в

общем случае разной величины и имеющих положительный знак при возрастании напряжения и отрицательный при его убывании.

Рис. 7.1. Входное напряжение цепи

Ток или напряжение любой ветви при переходном процессе можно найти

из суммы токов, вызываемых отдельными постоянными составляющими напряжения. Для применения этого метода необходимо предварительно рассчи-

тать переходный ток или напряжение исследуемой ветви цепи по заданному постоянному входному напряжению U0 или току I0 и найти зависимую от

времени переходную функцию K t , связывающую искомую и заданную величины. Например, при включении цепи r, L на постоянное напряжение ток

U

0

r

i

1

exp

t

.

r

L

Следовательно, переходная функция

K t

i

1

r

1

exp

t .

U0

r

L

В данном случае она имеет размерность проводимости и называется переходной проводимостью

Y t	1				t
	r	1	exp				,

где L / r — постоянная времени этой цепи.

Для постоянного напряжения, включенного позже на время x , переход-

ная проводимость

Y t x	1				t x
	r	1	exp			.

Аналогичным образом определяется любая переходная функция K t . Например, напряжение на индуктивности при включении r, L на постоянное напряжение U0 и переходная функция соответственно равны

			r					r
	uL U0 exp			t	,	K t exp			t .
			L					L

В этом случае переходная функция безразмерна. Переходная функция, в принципе, сразу определяет выходную величину, так как дает численное значение (но не размерность) выходной величины, когда входная (U0 или I0 ) равна

единице.

Составляющая переходного тока от напряжения u 0 , включаемого в начальный момент, равна Y t u 0 , а от скачка напряжения u , включаемого в

момент x x , равняется Y t x x . В результате приближенное значение

искомого переходного тока будет

			x t			x u .
	i t Y t u 0 Y t x
			x 0
	Точное значение тока i t получится при переходе x в пределе к беско-
нечно малым промежуткам времени d x .
Тогда		u d u u x d x ,
где		d u t
	u x d t				t x
и ток
					t
	i t Y t u 0		Y t x u x d x .

0

Это выражение называется интегралом Дюамеля. При определении напряжения какой-либо ветви в интеграле Дюамеля вместо переходной проводимости должна стоять соответствующая переходная функция.

Далее в виде примера определен ток при включении цепи r, L на затухающее по показательному закону напряжение u t U exp t / T , где T — постоянная времени, характеризующая скорость затухания u t . Переходные проводимости для этого случая даны выше, а

x

d u x

U

x

u 0 U , u x U exp

,

exp

.

u x

d x

T

T

T

После подстановки этих величин в интеграл Дюамеля и интегрирования

определяется искомый ток:

i t

1

t

t

1

t x

U

x

1 exp

U

1 exp

exp

d x

r

r

T

T

0

t

U

t

U

t

exp

t

t

1

exp

T exp

T

exp

1

r

1

1

r

T

T

T

t

t

U exp

exp

T

.

r

1

T

В частном случае, когда T , получается неопределенность, которая по-

сле раскрытия дает

U

r

i

t exp

t

.

L

L

Во всех случаях переходный ток положителен и имеет максимум im , определяемый обычным образом. При T

im eUr .

Применение метода наложения удобно также в тех случаях, когда напря-

жение, на которое включается цепь, представляет собой кусочноаналитическую кривую, имеющую разрывы. При этом переходный ток определяется как сумма интегралов Дюамеля за время отдельных участков u t , при-

чем в их первых членах Y t u 0 напряжение u 0 равно разности приложен-

ных напряжений после и до разрыва, с которого начинается данный участок. Импульсный интеграл Дюамеля. Метод наложения может быть также

применен, если заданное входное напряжение u t представить в виде следующих друг за другом прямоугольных импульсов напряжения u x малой длительности x (рис. 7.2) с последующим наложением выходной величины, на-

пример тока цепи, от каждого импульса напряжения с учетом его величины и сдвига во времени.

Рис. 7.2. Вид входного напряжения цепи

Прямоугольный импульс (рис. 7.3) характеризуется интенсивностью

S U1 t , равной произведению амплитуды импульса U1 на его длительность

t . Импульс с интенсивностью S 1 называется единичным.

Рис. 7.3. Преобразование входного напряжения цепи

Один прямоугольный импульс может быть представлен алгебраической

суммой двух одинаковых скачков постоянного напряжения U1 и U1 , из ко-

торых второй возникает на время t		позже первого. Тогда ток i1 t от рассмат-
риваемого импульса напряжения в момент t определяется с помощью переход-
ной проводимости, которая для первого			скачка равна Y t , а для второго
Y t t	i1 t Y t U1 Y t			t U1 .
Если на цепь воздействует		единичный		импульс				напряжения, т. е.
U1 t 1, предыдущее выражение получает вид
i t U1	t Y t	Y t	t Y t Y t					t .
1	t					t
При переходе к пределу t d t единичный импульс превращается в так
называемую единичную импульсную функцию, а ток
i1 t lim		Y t Y t		t
			t		Y t		.

t d t

Таким образом, аналогично численному равенству переходной проводимости Y t току от единичного скачка напряжения при единичной импульсной функции напряжения ток равен производной от Y t . Поэтому Y t называется

импульсной переходной проводимостью.

Для установления связи между искомым током i t , заданным напряже-

нием произвольной формы, разбитым на элементарные импульсы u x , и им-

пульсной переходной проводимостью можно идти тем же путем, как и при выводе интеграла Дюамеля, но проще это сделать, интегрируя его по частям:

t

i t Y t u 0 Y t x u x d x

0

t

Y t u 0 Y 0 u t Y t u 0 Y t x u x d x .

0

Отсюда получается импульсный интеграл Дюамеля:

t

i t Y 0 u t Y t x u x d x .

0

r 1 T

В общем случае в импульсный интеграл Дюамеля вместо u x следует

подставить заданную входную величину, а взамен Y t x							- соответствующую
импульсную переходную функцию K
				t x .
Далее в виде примера решается та же задача - определение переход-
ного тока i t при включении цепи				r, L		на напряжение	u t U exp t / T .
Здесь
Y t	1			r				x
		1	exp		t ,	u x U exp			,
	r			L
								T

			по ее аргументу t x , или, что то
Y t x есть производная функции Y t x
же самое, ее производная по t :
	1			t x
		exp			,
Y t x	L

где L / r - постоянная времени цепи. Из-за наличия индуктивности Y 0 0 , ток

x

t

1

t x

x

i t 0 U exp

exp

U exp

d x

T

L

0

T

t

U

t t

1

1

U exp

1

t

exp

exp

xd x

exp

1

1

L

0

T

T

L

T

t

t

U exp

exp

T

.

Таким образом, получен тот же результат, что и при применении первой

формы интеграла Дюамеля, но вычисления в данном примере несколько упро-

стились.

Область применения метода наложения. Из изложенного видно, что

метод наложения позволяет найти выходную величину переходного процесса

по заданной или полученной путем аппроксимации аналитической зависимости входной величины от времени. При этом следует применять ту форму интеграла Дюамеля, для которой подынтегральное выражение упрощается. Очевидно, что метод наложения применим только в случае интегрируемых функций.

7.2. Спектральный метод

Прямое и обратное преобразования Фурье. В п. 7.1 для расчета пере-

ходных процессов при включении цепи на непериодическое напряжение было применено его разложение на скачкообразные, или импульсные, напряжения с последующим применением принципа наложения. Эту задачу также можно ре-

шить, если представить непериодическую функцию в виде суммы гармоник.

Так как каждая гармоника ряда Фурье может быть записана в комплексной форме:

vk Vkm sin k t k ImVkm exp jk t

(Vkm — комплексная амплитуда), весь ряд Фурье может быть также записан в комплексной форме:

k m

f t V0 Im Vkm exp j k t .

k 1

Коэффициенты этого ряда, т. е. комплексные амплитуды гармоник, могут

быть определены из из данных п. 1.2 выражений для Ak и Bk :

V

V

exp j

k

V

km

cos

k

jV

km

sin

k

km

km

A

jB

k

1

f t sin k t j cos k t d t

k

j

j

f t cos k t j sin k t d t

f t

exp j k t d t .

Комплексная

амплитуда

гармоники

k

периодической функции

f1 1t f t

с периодом T 2 / 1

j

j

T

2

Vkm

f1 1t exp j k 1t d 1t

1

f

t exp j k 1t d t .

T

2

Непериодическую функцию можно рассматривать как предельный случай периодической, у которой период Т стремится к бесконечности. Тогда разница в частоте между двумя соседними гармониками будет стремиться к d .

Так как частота основной (первой) гармоники 1

, она также стремится к

d . Частота k 1 гармоники k должна быть обозначена через . Тогда общее выражение комплексной амплитуды гармоники частоты получает вид

Vm j d f t exp j t d t j d F j .

Таким образом, воздействие на цепь непериодической функции f t может быть заменено суммарным воздействием бесконечно большого числа бесконечно малых гармоник, т. е. воздействием спектра Vm . Относительные значения амплитуд гармоник пропорционально комплексной функции частоты F j , имеющей вид интеграла Фурье:

F j f t exp j t d t

и называемой спектральной характеристикой, или спектральной плотностью, функции f t . Эта характеристика может быть записана в показательной форме:

F j F exp j ( ) .

Тогда F называется амплитудно-частотной, a — фазо-частотной характеристикой.

Преобразование f t в F j , т. е. прямое преобразование Фурье, возможно, если интеграл Фурье имеет конечное значение. Так как exp j t 1, для этого достаточно, чтобы интеграл

f t d t ,

чего, например, не будет, если f t — постоянная величина, или синусоидаль-

ная функция.

Первым этапом спектрального метода расчета переходных процессов является преобразование оригинала f t в его изображение F j . Если U j является спектральной характеристикой напряжения, спектральная характеристика тока I j может быть найдена из закона Ома по известному комплексному сопротивлению Z j или проводимости Y j цепи, в общем случае

являющимися также комплексными функциями частоты. Тогда

I j UZ jj Y j U j .

В общем случае при задании какой-либо функции с характеристикой F1 j , воздействующей на вход цепи, характеристика искомой функции выхода

F2 j K j F1 j ,

где K j - так называемая передаточная функция. При изменении частоты

передаточная функция изменяется и по величине, и по фазе. В отличие от аналогичной величины — переходной функции, которая характеризует переходный процесс при воздействии на цепь постоянного напряжения (см. п. 7.1), передаточная функция K j характеризует установившийся процесс при сину-

соидальном воздействии.

После определения спектральной характеристики, т. е. изображения искомой величины, должен быть найден оригинал. Для вывода формулы обратно-

го преобразования F j в f t

может быть также использован переход от

дискретного ряда к непрерывному.

Ряд Фурье в комплексной форме имеет вид

k m

1 t

f1 1 t V0 Im

Vkm exp j k

k 1

Учитывая, что мнимая часть любого комплексного числа F

ˆ

F

F

Im F

2 j

,

ˆ

сопряженный

комплекс),

после

переходов

T ,

k 1 и

( F —

V

V

j d

F j получают следующее

значение непериодической

km

m

функции:

1

j d

1

j d

f

t

F j exp j t

F j exp j t

2 j

2 j

0

0

1

F

j exp j t d

F j exp j t

d

2

0

0

.

1

F j exp j t d

2

Постоянная составляющая ( 0 ) учтена тем, что нижний предел исходных интегралов взят равным нулю.

Это обратное преобразование Фурье служит для получения искомой функции времени по ее спектральной характеристике.

Необходимо отметить, что отрицательная частота имеет лишь математический смысл. Она возникает в результате замены синусоид показательными функциями exp j t .

Пример применения спектрального метода. В качестве примера рас-

сматривается переходный процесс включения цепи r, L на прямоугольный импульс напряжения U продолжительностью 0 . После окончания импульса кон-

тур остается замкнутым.

Для упрощения удобно представить импульс существующим с момента времени 0,5 0 до 0,5 0 (рис. 7.4, а). Так как вне этого промежутка времени

f t 0 , интеграл Фурье вычисляется только для 0,5 0 t 0,5 0 :

	U j		0,5		0 U exp j t					U				exp j t						0,50,5		0
										j
			0,5 0																			0
						0					0
				exp j				exp	j												0
		2U				2					2					2U	sin			2				.
								2 j

Это и есть спектральная плотность, которая в данном случае вещественна и изображается вектором, совпадающим с осью вещественных чисел.

Следовательно, фаза спектральной плотности равна нулю, когда

	sin	0
дробь		2	положительна, и равна , когда эта дробь отрицательна. Ампли-
тудно-частотная характеристика, очевидно, равна
				0
			U 2U	sin 2		,

откуда U 0 U 0 . Амплитудно-частотная и фазочастотная характеристики и изображены на рис. 7.4, б.

Так как сопротивление цепи Z j r j L , спектральная характеристика тока

	I j	U j			2U		sin	0 .
		Z j			r j L
								2

Переходный ток находят с помощью обратного преобразования Фурье:

		1		1		2U exp j t		0
	i t		I j exp j t d				sin		d .
		2		2
						r j L		2

Рис. 7.4. Импульс входного напряжения

что требует вычисления интеграла сравнительно сложной функции. Решение этой же задачи методом наложения (включение цепи на напряжение U при t 0 и на U при t 0 ) значительно проще.

Если требуется найти напряжение uL t на индуктивности, то, так как

	j L
U L	r j L	U	,

передаточная K j и спектральная U L j функции получают вид

	K j	j L	,	U L j K j U j .
		r j L

Определение искомого напряжения

uL t	1		2 j LU exp j t	sin	0	d
	2
			r j L		2

также связано с вычислением интеграла.

Область применения спектрального метода. Как видно из изложенно-

го, непосредственное применение спектрального метода имеет следующие ограничения:

1)он может применяться только для абсолютно интегрируемых функций;

2)этот метод принципиально не учитывает начальных условий, поэтому он применим только для задач с нулевыми начальными условиями.

Некоторые искусственные приемы позволяют обойти эти ограничения, но при этом расчеты еще больше усложняются. Как было видно из рассмотренного примера, наиболее трудным этапом является обратное преобразование, связанное с интегрированием сложных функций. В ряде случаев интегралы не берутся

иприходится прибегать к приближенным расчетам. Очевидно также, что спектральный метод как разновидность метода наложения применим только для линейных цепей.

Ценность спектрального метода заключается в том, что расчет переходных процессов сводится к расчету установившихся режимов в цепях синусоидального тока и, следовательно, к возможности получения ответа без составления и решения дифференциальных уравнений. Задачи могут быть решены при помощи определенных из опыта или заданных аналитически или графически амплитудно-частотных характеристик входных напряжений и токов цепи и передаточных функций. Этот метод в чистом или приближенном виде широко применяется в теории автоматического регулирования и радиотехнике.

Тесты для самопроверки

1. Какое интегральное преобразование используется в частотном методе? а. Интегральное преобразование Фурье; б. Интегральное преобразование Лапласа;

в. Используются оба преобразования, указанные в пунктах а и б; г. Не достаточно данных для ответа.

2. Можно ли определить по этому выражению спектральные характеристики мгновенных значений тока и напряжения

F( j ) f (t)e j t dt.?

0

а. Нет; б. Да; в. Только тока: г. Только напряжения.

3. Можно ли утверждать, что преобразование Фурье является частным случаем преобразования Лапласа при p j ?

а. Нет; б. Да; в. Не достаточно данных для ответа.

4. Какие характеристик можно определить по известной спектральной характеристике?

а. Только амплитудно-частотную F( ); б. Только фазочастотную ( ); в. Вольт-амперную; г. Амплитудно-частотную F( ) и фазочастотную

( ).

5. Что является частотной характеристикой цепи?

а. Отношение спектральных характеристик входного тока к входному напряжению;

б. Отношение спектральной характеристики выходного напряжения U 2 ( j ) к спектральной характеристике входного напряжения U1 ( j ) ;

в. Отношение спектральной характеристики входного напряжения U1(j ) к спектральной характеристике выходного напряжения U2(j );

6. Чему соответствует амплитудно-частотная характеристика цепи?

а. Модулю частотной характеристики; б. Аргументу частотной характеристики; в. Комплексной передаточной функции; Реактивной проводимости цепи.

7.Чему соответствует фазочастотная характеристика цепи? а. Модулю частотной характеристики; б. Аргументу частотной характеристики; в. Комплексной передаточной функции; г. Реактивной проводимости цепи.

8.Можно ли использовать частотный метод для нелинейных цепей?

а. Нет; б. Да; в. Не достаточно данных для ответа 9. Расчет переходных процессов частотным методом выполняют для цепей с нулевыми начальными условиями?

а. Нет; б. Да; в. Не достаточно данных для ответа 10. Что является передаточной характеристикой цепи?

а Отношение спектральных характеристик входного тока к входному напряжению;

б. Отношение спектральной характеристики выходного напряжения U 2 ( j ) к спектральной характеристике входного напряжения U1 ( j ) ;