Способы задания логических функций

Логические функции могут быть заданы одним из пяти способов:

1. Словесным описанием;

2. Табличным способом;

3. Числовым способом;

4. Аналитическим выражением;

5. Картами Карно.

1. Пусть логическая функция задана словесным описанием:

функция трех переменных принимает значение 1, если любые две переменные или все три равны 1; во всех других случаях эта функция принимает значение 0.

2. Представим эту функцию табличным способом, т. е. в виде таблицы истинности (табл. 5):

Таблица 5
Номер набора j	Х2	X1	Х0	У
0	0	0	0	0
1	0	0	1	0
2	0	1	0	0
3	0	1	1	1
4	1	0	0	0
5	1	0	1	1
6	1	1	0	1
7	1	1	1	1

3. Числовой способ задания функции заключается в перечислении номеров наборов j, на которых функция У принимает значение 1 (j=3, 5, 6, 7) или значение 0 (j=0, 1, 2, 4).

4. Аналитическое выражение логической функции можно получить по таблице истинности.

Из таблицы истинности проведем анализ четырех наборов переменных, на которых функция у принимает значение 1. Чтобы на наборах 3, 5, 6, 7 было у= 1, единице должна быть равна каждая из соответствующих конъюнкций, в которых х, записывают в инверсной форме, если он в этом наборе равен нулю (иначе конъюнкция не будет равна единице):

набор J=3, (Х₂,Х₁,Х₀)=011, Х₂Х₁Х₀= У=1;

набор J=5, (Х₂,Х₁,Х₀)=101, Х₂Х₁Х₀= У=1;

набор J=6, (Х₂,Х₁,Х₀)=110, Х₂Х₁Х₀= У=1;

набор J=7, (Х₂,Х₁,Х₀)=111, Х₂Х₁Х₀= У=1.

Каждое произведение переменных является минтермом и искомую функцию можно представить как дизъюнкцию минтермов:

. (1.1)

Такая запись представляет собой СДНФ искомой логической функции.

Можно представить заданную функцию в другой форме, если провести анализ четырех наборов переменных, на которых функция у принимает значение 0. Чтобы на наборах 0, 1, 2, 4 имело место у=0, нулю должна равняться дизъюнкция переменных из этого набора; если в данном наборе переменная равна единице, то в дизъюнкцию должна входить ее инверсия.

набор J=0, (Х₂,Х₁,Х₀)=000, Х₂Х₁Х₀= У=0;

набор J=1, (Х₂,Х₁,Х₀)=001, Х₂Х₁Х₀= У=0;

набор J=2, (Х₂,Х₁,Х₀)=010, Х₂Х₁Х₀= У=0;

набор J=4, (Х₂,Х₁,Х₀)=100, Х₂Х₁Х₀= У=0.

Каждое произведение переменных является макстермом и искомую функцию можно представить как конъюнкцию макстермов:

. (1.2)

Такая запись представляет собой СКНФ искомой логической функции.

4. Минимизация логических функции.

Минимизацией называют процедуру упрощения выражения логической функции, с тем, чтобы она содержала минимальное количество членов при минимальном числе переменных. Чем проще логические выражения, описывающие функции, тем проще и дешевле реализующая их схема.

В некоторых простых случаях минимизацию можно осуществить непосредственно используя основные законы булевой алгебры. В качестве примера упростим выражение (1.1), используя закон склеивания:

(1.3)

Полученное выражение равносильно исходному, но значительно проще его.

Следует отметить, что такие элементарные приемы минимизации удается использовать не часто — при малом количестве членов функции и небольшом числе переменных. В других случаях применяются графические методы минимизации, облегчающие поиск склеивающихся членов. К ним относится метод минимизации с помощью карт Карно.

Карта Карно – это таблица, построенная так, что в ее соседние клетки попадают смежные наборы переменных функции — наборы, отличающиеся значением одной переменной: в один набор эта переменная входит в прямой форме, а в другой — в инверсной. Благодаря этому возникает наглядное представление о различных вариантах склеивания смежных наборов.

Карта Карно имеет столько клеток, сколько комбинаций (наборов) можно составить из прямых и инверсных значений n переменных по n членов в каждой –2ⁿ. Так, при n =2 карта содержит четыре клетки (рис. 1.5, а), при n=3 - восемь клеток (рис. 1.5, б), при n =4 — шестнадцать клеток (рис. 1.5, в) и при n=5 – тридцать две клетки (рис. 1.5, г).

К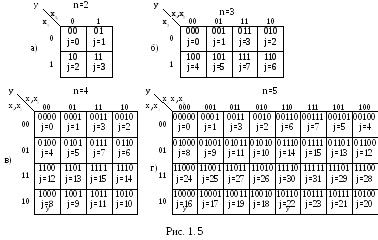аждые строка и столбец имеют строго определенную комбинацию значений переменных. Каждая клетка карты соответствует определенной комбинации значений переменных и могут быть обозначены номерами строк таблицы истинности –j.

Наборы переменных, на которых у= 1, т. е. минтермы функции, отмечаются в соответствующих клетках карты единицами. Наборы переменных, на которых у= 0, т. е. макстермы функции, отмечаются в соответствующих клетках карты нулями или их оставляют пустыми. Две стоящие в соседних клетках единицы — свидетельство того, что в составе СДНФ имеются наборы, отличающиеся значением одной переменной. Такие наборы склеиваются (объединяются в контуры). Аналогично, два стоящих в соседних клетках нуля также могут объединяться в контуры.

Минимизация функции заключается в объединении клеток карты с единицами (или нулями) контурами. Объединение каждой пары минтермов (макстермов) контуром уменьшает число входящих в них переменных на единицу.

Общие правила склеивания членов, занесенных в карту Карно, следующие:

1) охватывать контуром можно только соседние клетки;

2) контур должен быть только прямоугольным или квадратным и возможно большей площади;

3) количество клеток в контуре должно быть равно 2ⁱ, т. е. 2, 4, 8, 16 клеток;

4) контуры могут частично накладываться друг на друга;

5) крайние клетки строки, а также крайние клетки столбца карты считаются смежными; их можно таковыми представить, если мысленно свернуть карту в горизонтальный или вертикальный цилиндр;

6) количество охватывающих контуров должно быть минимальным.

Функция, минимизированная по единицам с помощью карты Карно, состоит из суммы простых конъюнкций. Каждая из них получается в результате склеивания членов, которым соответствует охваченные контуром единицы. В такую конъюнкцию войдут только те переменные, значения которых в пределах контура не меняются.

Порядок минимизации логической функции следующий:

1) построить карту Карно требуемого размера;

2) внести в карту единицы, соответствующие отдельным минтермам СДНФ функции;

3) охватить клетки карты возможно меньшим числом контуров. Чем больше клеток охвачено контуром, тем проще будет искомое выражение.

4) составить выражение для каждого контура;

5) записать минимизированное выражение функции.

Существует жёсткая однозначная связь между таблицей истинности, аналитическим выражением для функции и картой Карно.

Пусть логическая функция задана таблицей истинности (табл.5) или в СДНФ (1.1):

.

Непосредственно из таблицы истинности в клетки карты Карно (рис. 1.6) заносятся соответствующие значения функции у. Или в карту Карно можно занести только единичные значения для всех минтермов СДНФ функции.

В результате объединения клеток карты с единичными значениями получены три контура (черного цвета) по две клетки в каждом. Составив выражения для каждого контура, получим общую аналитическую запись функции:

(1.4)

Такая форма функции называется минимальной дизъюнктивной нормальной формой (МДНФ).

При объединении клеток карты с нулевыми значениями также получены три контура (голубого цвета) по две клетки в каждом. Составив выражения для каждого такого контура, получим общую аналитическую запись функции:

(1.5)

Полученная форма функции называется минимальной конъюнктивной нормальной формой (МКНФ).

Минимизация с помощью карт Карно не приводит к однозначной форме и для получения наиболее простой формы необходимо рассматривать всевозможные варианты склеивания.

При числе аргументов, большем пяти, используют обычно другие методы минимизации — применение карт Карно становится трудоемким.

Встречается необходимость минимизировать функцию, значения которой при некоторых комбинациях переменных не определены. Такой случай может иметь место, если значение функции при этих комбинациях безразлично или если определенные комбинации переменных невозможны по условиям задачи. На таких избыточных (запрещенных, факультативных) комбинациях можно придать функции любое значение — 0 или 1.

Пусть, например, функция представлена в виде карты Карно, изображенной на рис. 1.7. Здесь в клетках J=0 и J=1 функция у не определена и отмечена звездочкой (*). При объединении контурами единичных значений функции целесообразно клетке J=1 придать значение «1», а J=0 – значение «0». Тогда можно объединить в один контур 4 клетки. В результате аналитическая запись функции в форме МДНФ будет иметь следующий вид:

Рациональное доопределение функции может оказаться весьма эффективным для ее минимизации и, следовательно, для упрощения устройства, реализованного в соответствии с ней.