Posobie_MathCAD_v2

a1 6	a2 7	a3 0	a4 1
f(y) a1 a2 y a3 y2			a4 y3
z 2	x root (f(z) z)		x 3		f x			2.463 10 5
	1		1		1

z 0.5 z 3

					f(z)											f x
x2 root				z x			z			x		1								6.078 10 4
					1					2						2
					f(z)																	f x3
x	root		z x				z x				z		x		2								4
3													3										1.904 10
					1		2
		f(y)			10
					0
					10
							2						0					2

Рис. 1.15. Поиск корня полинома с понижением порядка

21

Глава 2. Численные методы линейной алгебры

Задачи линейной алгебры, успешно решаемые с помощью инструментов MаthCAD, можно условно разделить на следующие группы:

простейшие матричные операции (транспонирование, сложение, умножение на константу, перемножение матриц), которые сводятся к определенным арифметическим действиям над элементами матриц;

вычисление определителей матриц, нахождение обратных матриц;

решение систем линейных алгебраических уравнений (СЛАУ);

вычисление собственных значений и собственных векторов.

2.1. Матрицы и простейшие операции над ними

Вещественной матрицей размерности m n назовем таблицу из m строк и n столбцов, составленную из вещественных чисел:

x		x		x
	11	12		1n
x21		x22		x2n
X						{x }j 1,...,n .		(2.1)
						ij	i 1,...,m
		xm2
xm1				xmn
Пусть	A {a } j 1,...,n		,	B {b } j 1,...,n			– матрицы одинаковой
		ij i 1,...,m			ij	i 1,...,m

размерности. Для них можно определить операцию сложения:

C A B,	C {c	}j 1,...,n	,	c		a b ,		i 1, ...,m, j 1, ...,n ,
	ij	i 1,...,m		ij		ij	ij
умножения на числовую константу:
C A,	C {c }j 1,...,n ,			c	a ,		i 1, ...,m, j 1, ...,n .
	ij	i 1,...,m		ij		ij

Операцию умножения матриц можно определить для матриц

A {a	} j 1,...,n	, B {b } j 1,...,l , тогда
ij	i 1,...,m		ij i 1,...,n
				n
	C A B,		j 1,...,l	cij aik bkj .	(2.2)
			C {cij }i 1,...,m ,

k 1

22

Транспонирование - это операция, переводящая матрицу размера m n в матрицу размера n m. При этом строки исходной матрицы становятся столбцами транспонированной и наоборот. Транспонированную матрицу обычно обозначают A . Элементы транспортированной матрицы A связаны с элементами исходной матрицы A простым соотношением: a ij = aji.

Можно показать, что для матричных операций справедливо:

A + B = B + A

(A + B) + C = A + (B + C)

(A B) C = A (B C)

существование нулевой матрицы O: A + O = A

существование обратной по отношению к операции сложения матрицы –A, такой, что A + ( –A ) = O

существование		единичной матрицы I, A I = I A = A,
1	0 ...	0
I 0	1 ...	0
... ... ...		...
0	0 ...	1

A B B A (нет коммутативности операции умножения) Нормой матрицы A называется скалярная величина, удовлетворяющая условиям:

1) A 0 , и если A 0, то A - нулевая матрица

2) A A вещественного

3) A B A B для любых матриц A, B.

Вкакой-то степени норму A можно образно представлять как величину, характеризующую все элементы матрицы. В качестве нормы матрицы используют различные величины, например:

n

A max aij . Возможны и другие определения нормы

j i 1

[Ошибка! Источник ссылки не найден.1].

23

2.2. Определитель, ранг, обратная матрица

Рассмотрим несколько важных операций линейной алгебры, которые также реализованы в MathCAD в виде стандартных функций. Однако их применение требует гораздо большего внимания пользователя, чем операции, описанные в предыдущем параграфе.

Определителем (детерминантом) квадратной матрицы A порядка n называется многочлен порядка n, в котором каждое слагаемое содержит по одному элементу из каждой строки и по одному элементу из каждого столбца матрицы, причем члены ряда суммируются с учетом индексов элементов, входящих в сомножитель. Суммирование идет по всем возможным перестановкам порядка n, поэтому число слагаемых в ряде равно n!.

Определители первого, второго и третьего порядков вычисляются по простым формулам:

1

a11

2

a11

a22

a21 a12

a .

(2.3)

3

a

a

22

a

a

a

23

a

a

21

a

11

33

12

31

32

13

a31

a22

a13

a21

a12

a33

a11

a23

a32

Определитель порядка n вычисляется по формуле

n

( 1)N ( 1 , 2 ,..., n ) a 11 a 2 2 ... a nn ,

(2.4)

1 , 2 ,..., n

где 1,2 ,...,n -

перестановки

чисел

от 1

до n,

N ( 1, 2 ,..., n ) - число инверсий в перестановке.

Понятие определителя играет важную роль в вычислении ранга матрицы и обратной матрицы. Рангом матрицы называется наибольшее натуральное число k, для которого существует отличный от нуля определитель k-ого порядка подматрицы, составленной из любого пересечения k строк и k столбцов исходной матрицы. Если ранг квадратной матрицы A порядка n сов-

падает с ее порядком, т.е. n 0 то матрица называется невырожденной, и для нее можно определить так называемую об-

24

Рис. 2.1. Панель инструментов «Матрица»

ратную матрицу A-1, обладающую следующим свойством: A A 1 A 1 A I , где I – единичная матрица.

2.3. Операции с матрицами в MathCAD

Описанные выше операции реализованы в MathCAD в виде операторов, запись которых максимально приближена к математическим выражениям. При этом для матричных операций зачастую используются те же знаки математических операций, что и для скаляров, однако вычисления проводятся по приведенным выше формулам.

Заметим, что векторы являются частным случаем матриц размерности N 1 (вектор-столбец). Кроме стандартных матричных операций к векторам можно применять ряд специфических операций (модуль вектора, скалярное и векторное произведение и др.). Для того чтобы аналогичные действия выполнить с вектор - строкой, т.е. матрицей размерности 1 N, ее нужно сначала транспонировать.

Для работы с матрицами и векторами предназначена панель инструментов Matrix (Матрица), показанная на рис. 2.1. В таблице 2.1. приведен список операций и функций с матрицами и векторами, а на рис. 2.2 и 2.3. – некоторые примеры их использования.

Таблица 2.1. Операции с матрицами и векторами

Название	Вызов/обозначение	Горячие
операции	в MathCAD	клавиши
Создание матриц	Меню: Insert – Matrix	<Ctrl>+<M>
	Панель инструментов:
Обращение к	Панель инструментов:	< [ >
элементу матри-
цы
Выделение	Панель инструментов:	<Ctrl>+<6>
столбца

25

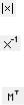
Создание еди-	Identity(N), N - размерность					-
ничной матрицы	матрицы
Создание матрицы	Diag(V), V – вектор главной					-
из вектора	диагонали
Создание матриц	Matrix(M,N,f),					-
на основе функции	M, N	–	размерность		матрицы,
	f (i,j) – функция, задающая
	элемент матрицы
Размерность	rows(A)		– число строк A			-
матрицы A /	cols(A) -число столбцов A
вектора v	length(v)			– число	элементов
	вектора
	last(v) - индекс последнего
	элемента вектора
Выделение под-	Submatrix(A,ir,jr,ic,jc) -					-
матрицы из мат-	часть матрицы между строками
рицы A	ir,jr и столбцами ic,jc
Слияние матриц	augment(A,B,C,...) - новая					-
	матрица формируется слиянием
	матриц		аргументов		слева –
	направо;
	stack(A,B,C,...) - новая мат-
	рица	формируется			слиянием
	матриц аргументов cверху -
	вниз
Ранг матрицы	rank(A)					-
Определитель	Панель инструментов:					<Shift>+<\
матрицы						>
Обратная матрица	Панель инструментов:
Умножение мат-	A*B
риц A, B
Транспонирование	Панель инструментов:					<Ctrl>+<1>
матрицы
Норма матрицы A	norm1(A),			norm2(A),		-
	norme(A), normi(A)

26

а

б		в

г

Рис. 2.2. Фрагменты рабочего листа MathCAD, представляющие создание матрицы (а), сложение матриц (б), произведение матриц (в), нахождение определителя и обратной матрицы (г)

Рис. 2.3. Фрагмент рабочего листа MathCAD, представляющий умножение матриц несоответствующих размерностей

27

2.4. Системы линейных алгебраических уравнений

Пусть задана система линейных алгебраических уравнений (СЛАУ) размерности m, которую можно записать в скалярном:

a11 x1 a12

x2 ... a1m xm f1

x1 a22

x2 ... a2m xm f2

a21

(2.5)

...

a

m1

x

a

m2

x

2

... a

mm

x

m

f

m

1

векторном:

a11

a12

a1m

f1

a21

x

a22

x

...

a2m

x

f2

(2.5 )

2

m

...

1

...

...

...

am1

am2

amm

fm

или матричном виде:

(2.5 )

Ax

f ,

a11

a12

...

a1m

f1

x1

f2

x2

где

A

a21

a22

...

a2m

,

, f

...

x

...

.

fm 1

xm 1

am2

...

f

m

x

m

am1

amm

Здесь A – матрица системы,

f

– вектор правых частей,

x

– век-

тор неизвестных. Назовем расширенной матрицей системы матрицу A , дополненную столбцом вектора правых частей:

	a11	...	a1m	f1
A	a21	...	a2m	f2		.
				...
		...	amm
	am1			fm

Система имеет решение, если det A 0. По определению решения, подставив вектор x в СЛАУ, получим m тождественных уравнений.

Эффективность способов решения системы (2.5) во многом зависит от структуры и свойств матрицы A: размерности, обу-

28

словленности, симметричности, заполненности (т.е. соотношения между числом ненулевых и нулевых элементов) и др.

Все методы решения СЛАУ можно разбить на два класса: прямые (точные) и итерационные (приближенные).

Прямые методы позволяют получить решение за конечное число арифметических операций. Если операции реализуются точно, то и решение будет точным (поэтому класс прямых методов еще называют точными методами). В итерационных методах решением является предел некоторой бесконечной последовательности единообразных действий.

2.5. Точные методы решения СЛАУ

При небольшой размерности системы m можно использовать формулы Крамера, которые позволяют находить неизвестные в виде дробей, знаменателем которых является определитель матрицы системы, а числителем – определители матриц Ai, полученных из A заменой столбца коэффициентов при вычисляемом неизвестном столбцом вектора правых частей:

xi detdet AAi (i = 1, 2, …, m).

Размерность системы (т.е. число m) является главным фактором, из-за которого формулы Крамера не могут быть использованы для численного решения СЛАУ большого порядка. При непосредственном раскрытии определителей решение системы с m неизвестными требует порядка m!m арифметических операций. Таким образом, для решения системы, например, из m = 100 уравнений потребуется совершить 10158 операций, что не под силу даже самым мощным современным ЭВМ.

Для решения небольших систем используют метод обратной

матрицы. Если det	A 0, то существует обратная матрица
A–1. По определению	обратной матрицы: A A–1 = A–1 A = I, где I –

единичная матрица. Если обратная матрица известна, то, умножая на нее СЛАУ слева, получим:

A 1 Ax	A 1 f ,	I x	A 1 f ,	x	A 1 f .

29

Следовательно, решение СЛАУ свелось к умножению известной обратной матрицы на вектор правых частей. Таким образом, задача решения СЛАУ и задача нахождения обратной матрицы связаны между собой, поэтому часто решение СЛАУ называют задачей обращения матрицы. Проблемы применения этого метода те же, что и при использовании метода Крамера: нахождение обратной матрицы – трудоемкая операция.

Наиболее популярным точным способом решения линейных систем вида (2.5) является метод Гаусса, или последовательного исключения неизвестных. Метод состоит из двух этапов: прямого и обратного. На первом этапе исходная система с помощью эквивалентных преобразований сводится к системе с треугольной матрицей, на втором этапе решается система с треугольной матрицей. Эквивалентными преобразованиями будут следующие преобразования расширенной матрицы А :

перестановка строк;

умножение строк на ненулевую константу;

сложение строк.

Используя эти преобразования, перепишем исходную систему так, чтобы один из коэффициентов столбца был равен 1, а все коэффициенты, стоящие ниже, были равны 0.

Пусть в исходной системе уравнений

a(0)	x	a(0)	x		... a(0)	x		f (0)
11	1	12		2	1m		m	1
a21(0)	x1 a22(0)		x2		... a2(0)m xm f2(0)
...
a(0)	x a(0)		x	2	... a(0)	x	m	f (0)
m1	1	m2			mm			m

первый элемент a11(0) 0 . Назовем его ведущим элементом пер-

вой строки. Поделим все элементы этой строки на a11(0) и исклю-

чим x1 из всех последующих строк, начиная со второй, путем вычитания первой (преобразованной), умноженной на коэффи-

циент при x1 в соответствующей строке. Получим

30