Posobie_MathCAD_v2

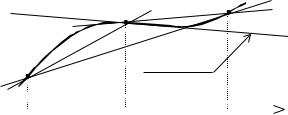
'	xi				fi 1 fi
f
					h	,		(5.1)
'	xi				fi fi 1
f
					h	,		(5.2)
f '	x			fi 1 fi 1			.	(5.3)
	i				2h

Геометрически вычисление производной по трем этим формулам эквивалентно замене касательной в точке B прямыми BС, AB и AC соответственно и поиску тангенса угла наклона этих прямых вместо тангенса угла наклона касательной (рис. 5.1).

								fi+1
					fi-1
									C
						B
	fi-1							касательная
		A
	xi-1				xi			xi+1

Рис. 5.1. Геометрическая интерпретация разностного дифференцирования

Изучим вопрос о порядке точности (аппроксимации) этих формул. Разложим f(x) в ряд Тейлора в окрестности точки xi.

f

f

hf

h2

f

h3

f ..., f

f

hf

h2

f

h3

f ....

i 1

i

i 1

i

i

2

i

6

i

i

2

i

6

i

Подставив эти разложения в (5.1), получаем

f

hf

h2

f

h3

f ... f

2

i

i

h

h

'

xi

i

2

i

6

i

fi

fi

fi ...

f

h

2

6

Здесь fi – первая производная, которую необходимо найти, а

h

f

h2

f .. – погрешность, с которой вычисляется производ-

2

i

6

i

ная. Видим, что первый член погрешности имеет порядок h, значит, при измельчении шага сетки погрешность будет умень-

81

шаться пропорционально h 1. Поэтому говорят, что формула имеет первый порядок точности. Нетрудно показать, что формула (5.2) также имеет первый порядок аппроксимации.

Покажем, что формула центральной разности имеет второй порядок точности. Подставим в (5.3) разложения для fi+1 и fi–1

f

hf

h2

f

h3

f ...

f hf

h2

f

h3

f ...

2

f '

x

i

i

2

i

6

i

i

2

i

6

i

i

f

h

f ...

i

2h

i

6

i

Погрешность вычисления производной пропорциональна h2, значит формула (5.3) имеет второй порядок аппроксимации.

Основываясь на понятии конечных разностей, можно получить формулы для аппроксимации производных высших порядков. Покажем это на примере формулы центральной разности для аппроксимации второй производной.

f '' x		fi fi		fi 1 fi fi fi 1		fi 1 2 fi fi 1 .
i		h2		h2		h2

Можно доказать, что эта формула имеет второй порядок точности (доказать самостоятельно).

Наконец, третьим способом получения формул численного дифференцирования является метод неопределенных коэффициентов. Представим приближенно в точке х = х0 k–ю производную таблично заданной функции в виде линейной комбинации ее значений в узлах

N
f k x0 Ci f xi .	(5.4)
i 1

где Ci – числовые коэффициенты, которые выберем из условия, чтобы эта формула была точна для многочлена максимально высокой степени. Иными словами потребуем, чтобы для функ-

m

ции P x a j x j приближенное выражение (5.4) было точным.

j 0

Для этого необходимо и достаточно, чтобы для любой степени

коэффициенты		при	aj	были	равны.	Поскольку
k	j j 1 ... j k 1 x j k ,			получаем	линейную систему
x j

уравнений относительно Ci:

82

N		j j 1 ... j k 1 x j k ,	j 0, 1,..., m .
C x j
i	i	0
i 1

Если m = N–1, то число уравнений равно числу неизвестных. Можно показать, что определитель такой системы не обращается в нуль. Очевидно, что m k, N k+1. При этом точность вычисления производной имеет порядок O(hm+1–k), хотя при определенном положении узлов (обычно это симметричное положение относительно точки xi) порядок многочлена, а следовательно, и точность можно повысить на единицу.

Пример 5.1. Задана функция f x sin x , x 0, 1 . Вычис-

лить значение производной на правой границе (в точке x = 1) c первым и со вторым порядком точности (h = 0,1).

Решение. Для вычисления производной составим таблицу значений функции

	i	N		N–1	N–2
	x	1		0.9	0.8
	f	0.841		0.783	0.717
Точное значение производной				f xN cos xN 0.540 .

Находим производную по формуле «разность назад»:

	f xN	fN fN 1		0.841 0.783	0.581 .
		h		0.1

Как было показано выше, формула имеет первый порядок точности. Для вычисления производной со вторым порядком воспользуемся методом неопределенных коэффициентов. Обозначим x на правой границе через xN. Требуется построить метод второго порядка, поэтому необходимо использовать три точки

xN , xN–1, xN–2, (xN–2 = xN – 2h, xN–1 = xN – h), тогда f ' xN C1 f xN 2 C2 f xN 1 C3 f xN .

Степень полинома будет m = N – 1

P(x) = a0 +a1x + a2x2 , P (xN) =a1+ 2a2xN

Подставляем P(x) в выражение для

f ' xN

f ' x

N

C

a a x

N 2

a x2

1

0

1

2 N 2

C

a a x

N 1

a x2

C

a a x

N

a x2

.

2 0

1

2 N 1

3

0 1

2 N

83

Собираем коэффициенты при a0 ,a1, a2 и, учитывая, что эти коэффициенты должны быть равны в выражении для P’(xN) и

f ' xN , получаем СЛАУ.

C C C 0,			2h C h C 1,		4h2 C h2	C 0 .
1	2	3	1	2	1	2

Отсюда C1 21h ;C2 4 21h ;C3 3 21h ; тогда

	f xN	3 fN 4 fN 1 fN 2		3 0.841 4 0.783 0.717	0.542 .
		2h		2 0.1

Видно, что формула второго порядка гораздо точнее формулы первого порядка.

С помощью MathCAD можно вычислять производные скалярных функций любого количества аргументов, от 0-го до 5-го порядка включительно. И функции, и аргументы могут быть как действительными, так и комплексными. Невозможно дифференцирование функций только вблизи точек их сингулярности.

Вычислительный процессор MathCAD обеспечивает превосходную точность численного дифференцирования. При этом символьный процессор позволяет вычислять производные громоздких функций, поскольку, в отличие от всех других операций, символьное дифференцирование выполняется успешно для подавляющего большинства аналитически заданных функций.

Первая производная

Для того чтобы продифференцировать функцию f(x) в некоторой точке:

1.Определяем точку x, в которой будет вычислена производная, например, x:=1.

2.Вводим оператор дифференцирования нажатием кнопки Derivative (Производная) на панели Calculus (Вычисления) или вводим с клавиатуры вопросительный знак <?>.

3.В появившихся местозаполнителях вводим функцию, зависящую от аргумента x, т.е. f(x), и имя самого аргумента x.

4.Вводим оператор численного <=> или < > символьного вывода для получения ответа.

84

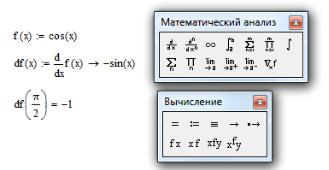
Пример 5.2. На листинге ниже приведен пример численного и символьного дифференцирования:

Для численного дифференцирования MathCAD применяет довольно сложный алгоритм, вычисляющий производную с колоссальной точностью до 7-8 знака после запятой. Этот алгоритм (метод Риддера) описан во встроенной справочной системе MathCAD, доступной через меню Help (Справка). Погрешность дифференцирования не зависит от констант TOL или CTOL, в противоположность большинству остальных численных методов, а определяется непосредственно алгоритмом.

Производные высших порядков

MathCAD позволяет численно определять производные высших порядков от 0-го до 5-го включительно. Чтобы вычислить производную функции f(x) N-го порядка в точке x, нужно проделать те же самые действия, что и при взятии первой производной, за тем исключением, что вместо оператора производной необходимо применить оператор N-й производной (Nth Derivative). Этот оператор вводится с той же панели Calculus (Вычисления), либо с клавиатуры <Ctrl> + <?>, и содержит еще два местозаполнителя, в которые следует поместить число N. «Производная» при N = 0 по определению равна самой функции, при N =1 получается обычная первая производная. Важно перед оператором дифференцирования не забывать присваивать аргументу функции значение, для которого будет вычисляться производная.

85

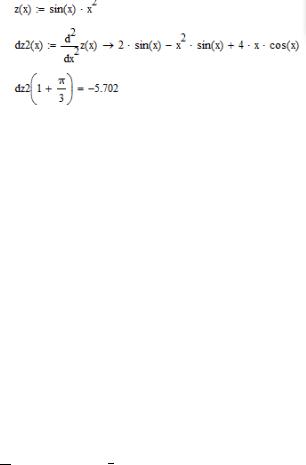
Чтобы вычислить производную порядка выше 5-го, следует последовательно применить несколько раз оператор N-й производной подобно тому, как вводятся операторы кратного интегрирования. Однако для символьных вычислений этого не требуется — символьный процессор умеет считать производные порядка выше 5-го.

Пример 5.3. Рассмотрим образец численного и символьного вычисления второй производной:

Расчет производных высших порядков производится тем же вычислительным методом Риддера, что и расчет первых производных. Причем для первой производной этот метод обеспечивает точность до 7-8 значащих разрядов числа, а при повышении порядка производной на каждую единицу точность падает примерно на один разряд.

Частные производные

С помощью символьного и численного процессоров MathCAD можно вычислять производные функций любого количества и по разным аргументам, т.е. частные производные. Чтобы вычислить частную производную, необходимо ввести оператор производной с панели Calculus (Вычисления) и в соответствующем местозаполнителе напечатать имя переменной, по которой должно быть осуществлено дифференцирование.

Пример 5.4. Символьное и численное вычисление частных производных в пакете MathCAD выглядит следующим образом:

f (x y) x2 y cos(x) y

x

f (x y) 2 x2y yx sin(x) y

86

			f (x y) 2 x2y		ln(x) cos(x)
	y
	x 1			y 0.1

y

f (x y) 0.54

y

f (x y) cos(1)

Как показано в примере, в первой строке определена функция двух переменных, а в двух следующих строках символьным образом вычислены ее частные производные по обеим переменным x и y соответственно. Чтобы определить частную производную численным методом, необходимо предварительно задать значения всех аргументов. При этом частные производные высших порядков рассчитываются точно так же, как и обычные производные высших порядков.

Также имеется возможность выбора формы записи частной производной, причем вид записи не влияет на вычисления, а служит лишь более привычной формой представления расчетов. Для того чтобы изменить вид оператора дифференцирования на представление частной производной, следует:

1.Вызвать контекстное меню из области оператора дифференцирования нажатием правой кнопки мыши.

2.Выбрать в контекстном меню верхний пункт View Derivative As (Показывать производную как).

3. В появившемся подменю выбрать пункт Partial Derivative (Частная производная).

Чтобы вернуть вид производной, принятый по умолчанию, выберите в подменю пункт Default (По умолчанию) либо, для представления в обычном виде - Derivative (Производная).

5.2. Численное интегрирование

Интегрирование функций является составной частью многих научных и технических задач. Поскольку аналитическое интегрирование не всегда возможно, используют различные методы численного интегрирования.

Математическая постановка задачи: необходимо найти значение определенного интеграла

87

b

I f x dx ,

a

где a, b – конечны, f(x) – непрерывна на [а, b]. Из математического анализа хорошо известна формула Ньютона–Лейбница для нахождения определенного интеграла c помощью первообразных. Однако первообразную можно найти не для всех функций, для некоторых элементарных функций первообразной вообще не существует. Поэтому строятся формулы приближенного интегрирования, которые называются квадратурными фор-

мулами.

При решении практических задач часто бывает, что интеграл неудобно или невозможно взять аналитически: он может не выражаться в элементарных функциях, подынтегральная функция может быть задана в виде таблицы и пр. В таких случаях применяют методы численного интегрирования.

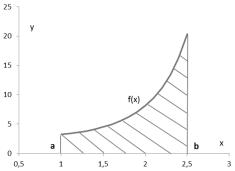
Известно, что определенный интеграл численно равен значению площади фигуры, ограниченной подынтегральной функцией, осью х, прямыми x=a и x=b (рис. 5.2). Общий подход к вычислению интеграла численными методами сводится к нахождению этой площади. Чаще всего интервал [а, b] разбивают на множество меньших интервалов. Находят приблизительно площади каждой части и потом сумму всех площадей.

Рис. 5.2. К объяснению геометрического смысла определенного интеграла

88

Хорошо известно, что для функций, допускающих на промежутке [a, b] конечное число точек разрыва первого рода, такое значение существует единственно и может быть формально получено по определению:

n	i xi xi 1 ,
I lim f		(5.5)
n i 1
где xi — произвольная	упорядоченная система точек	отрезка

[a, b], а i — произвольная точка элементарного промежутка

[xi–1, xi].

Простейшие квадратурные формулы выводятся непосредственно из определения интеграла, т.е. из представления (5.5). Зафиксировав некоторое n 1, будем иметь

n	xi xi 1 .
I f i		(5.6)

i 1

Это приближенное равенство назовем общей формулой прямоугольников. Геометрически площадь криволинейной трапеции приближенно заменяется площадью ступенчатой фигуры, составленной из прямоугольников, основаниями которым служит [xi–1, xi], высотами - ординаты f i .

Рассмотрим ряд наиболее употребительных квадратурных формул. Условимся в дальнейшем пользоваться равномерным разбиением отрезка [a, b] на n частей точками xi с шагом

h	b a	, полагая x0 = a, xi = xi–1 + h, xn				= b.	При таком разбие-
	n
нии формула (5.6) приобретает вид
			n
		I h f i ,		i [xi–1, xi].				(5.7)
			i 1
Теперь дело за фиксированием точек						f i на элементарных
отрезках[xi–1, xi]. Рассмотрим три случая.
1) Положим			i = xi–1.	Тогда	из		(5.7)	получаем
	n		n 1
I h f xi 1			h f xi . Эта формула называется формулой
	i 1		i 0

левых прямоугольников. Ее геометрическая интерпретация приведена на рис. 5.3.

89

a

b

x

Рис. 5.3. Геометрическая интерпретация формулы

левых прямоугольников

2) Пусть i = xi. Тогда имеем

n

I h f xi .

i 1

Это формула правых прямоугольников.

3) Фиксируем

1

x

x

.

В результате получим квадра-

i

i

i 1

2

турную формулу средних прямоугольников:

n 1

h

n

h

I h f xi

h f xi

.

i 0

2

i 1

2

Покажем, что эта формула имеет второй порядок точности. Рассмотрим сначала вычисление интеграла на отрезке [-h/2, h/2],

h2

f x dx hf0 ,

h2

где f0 = f(0). Пусть

x
F x f x dx,	F 1 2 F h 2 ;
0

h2

f x dx F h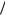2 F h2 .

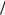h2

Разлагая в ряд Тейлора с остаточным членом в форме Лагранжа, имеем

F		h	f			h2	f '		h3		f ''		,
1 2	2			0	8		0	48

90