ЛАБ_ПРАК_MathCad

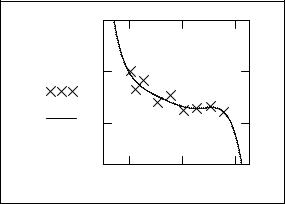
max(y)+1 2

y

1

P(z)

0

min(y)−1

0	2	4
min(x)−1	x,z	max(x)+1	.

2. Функцию аппроксимации можно построить с помощью встроенных возможностей MathCad. Но если все выше указанные вычисления мы можем проводить для не отсортированной выборки, то встроенные функции MathCad требуют, чтобы выборка была отсортирована по x.

После того, как выборка отсортирована, можно построить вектор базисных функций:

		cos(x)
		x2
F(x) :=		ex
		ln(x + 1)
		sin(x)	.

Далее ищем коэффициенты пробной функции с помощью встроенной функции пользователя linfit

A := linfit( x , y , F ) ,

где x, y – элементы выборки; F – вектор базисных функций.

Теперь можно построить аппроксимацию g: 51

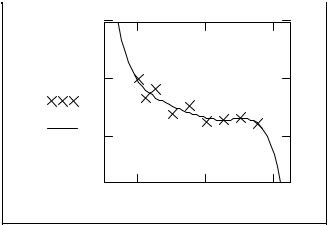
g(t) := F(t) A.

Для графического представления g(z) необходимо задать интервал изменения переменной z и шаг z:

z:= −1 ,−0.9..5.2.

Врезультате получим, что график имеет вид:

max(y)+1 2

y	1
g(z)
	0

min(y)−1

0	2	4
min(x)−1	x,z	max(x)+1	.

3. Сравним полученные результаты. Для этого вычислим относительную разницу между аппроксимациями полученными в пункте 1 и в пункте 2:

f(x) :=		P(x) − g(x)
			P(x)		.

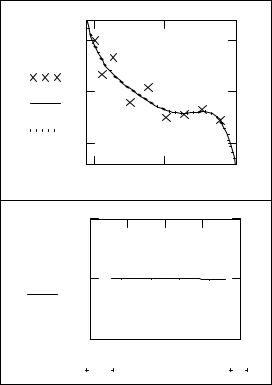
На первом графике представлены точки выборки и кривые аппроксимации из пункта 1 и пункта 2, а на втором – относительная разница f(x).

52

1.2

	1
y
P(z)	0.5
g(z)
	0
− 0.2	0	2	4
	− 0.2	x,z	4
0.2	0.2

f(z) 100 0

− 0.2		0.2
				2		0	2		4	6
			− 0.9				z			5.2		.

ЛАБОРАТОРНАЯ РАБОТА № 5 «Методы решения дифференциальных уравнений»

Цель работы: Познакомить читателя со встроенными возможностями пакета MathCad для решения дифференциальных уравнений (ДУ).

53

Рекомендуемая литература: [1-4, 6, 8-10].

Задание:

1.По заданной правой части ДУ первого порядка с разделяющимися переменными построить решение при помощи встроенных функций MathCad.

2.Построить разностную схему для ДУ из пункта 1.

3.Сравнить полученные в пунктах 1 и 2 решения.

4.Найти общее решение линейного неоднородного ДУ первого порядка.

5.Сделать проверку найденного в пункте 4 решения.

6.Найти решение неоднородного ДУ второго порядка с заданными начальными условиями.

Таблица № 5.1: Варианты лабораторной работы № 5 «Методы решения дифференциальных уравнений».

№	ДУ с разделяющи-	Неоднородное ДУ
	мися	первого порядка
	переменными
1	2	3
1	y'= y (x2 +1)	y'= 2 y − x
	y(0)=0.5	y(0)=1
	x [0; π]
1	2	3
2	y'= (ln( y) +1) sin(x)	x2 y + y2 − 2xy y'= 0
	y(0)=3	y(0)=1
	x [0; π]
3	y'= y cos(x)	y'=	y	−	x
	y(0)=0.2		x	3
	x [0; π]	y(0)=1

54

4

y'= ex sin( y)

y'−

3y

= x

y(0)=1.5

x

x [0; π]

y(0)=1

5

y'= e−y sin(x)

y'+

2 y

e−x2

y(0)=1.5

=

x

x

x [0; π]

y(0)=1

6

y'= e−y sin 2 (x)

y' cos(x) − y sin(x) = sin(2x)

y(0)=0.5

y(0)=1

x [0; π]

7

y' = y cos(x)

y' x + y = −x2 y

y(0)=0.45

y(0)=1

x [0; π]

8

y'= x e y

y'−xy = −e−x2

y(0)=0

y(0)=1

x [0; 1]

9

y'= cos( y) sin(x)

1

1

y(0)=0.25

x y' cos

= y cos

− x

x

x

x [0; π]

y(0)=1

10

y'= x +1 e y

x2 y'= x2 + xy

y(0)=-1

y(0)=1

x [0; 1]

1

2

3

11

y'= e−y cos(x)

x y'+y = ln(x) +1

y(0)=1.5

y(0)=1

x [0; π]

12

y'= cos( y) x2 +1

x2 y'+yx3 =1

y(0)=-1

y(0)=1

55

x [0; 1]

13

y'= cos( y)

x

y' sin(x) − y cos(x) =1

y(0)=0.35

y(π/2)=0

x [0; π]

14

y'=

1

sin(x)

y'−y sin(x) = e−cos( x) sin(2x)

y

y(π/2)=3

y(0)=-2

x [0; 1]

15

y'=

y sin(x)

y'+

2y

= −x

2

y(0)=0.15

x

x [0; π]

y(3)=1

16

y'= sin( y)

x2

+1

y'+y =

e−x

y(0)=-1.5

1+ x2

x [0; 1]

y(2)=0

17

y'= y

2

x

(1 + x2 ) y'−2xy = (1+ x2 )2

sin

y(-2)=5

2

y(0)=0.45

x [0; π]

18

y'=

1

cos(x)

x y'−2y = x3 cos(x)

y

y(π)=1

y(0)=-1

x [0; 1]

1

2

3

19

y'= sin( y) x2

y' x ln(x) − y = 3x3 ln2 (x)

y(0)=-0.5

y(e)=0

x [0; π]

20

y'= ln(y)

x2

+1

y'+2xy = xe−x2

y(0)=1.5

y(0)=4

56

x [0; 1]

21

y'= y ex

y'cos(x) − 2 y sin(x) = 2

y(0)=2.5

y(0)=3

x [0; π/2e]

22

y'=

1

ln(x +1)

y'−

3y

= x3e x

x

y

y(0)=1

y(1)=e

x [0; 1]

23

y'= y ex

x y'−3y = x4ex

y(0)=1.5

y(1)=e

x [0; π]

24

y'= e y

x2

+1

y'cos(x) + y sin(x) =1

y(0)=-1.5

y(0)=2

x [0; 1]

25

y'=

y

2

+1 sin(x)

y'+

y

sin(x)

=

y(0)=0.5

x

x

y(π/2)=1

x [0; π]

26

y'=

1

ex

y'−

y

= −2 ln(x)

y

x

y(0)=-3

y(1)=1

x [0; 1]

1

2

3

27

y'= y 2 у−2 x

1

x y'+2 y =

y(0)=1

x

x [0; π]

y(3)=1

28

y'= y 2

x2

+1

y'−y cos(x) = −cos(x)

y(0)=-5

y(0)=3

57

	x [0; 1]
29	y'= x2 ln(y) + x2	y'+2xy = e−x2 sin(x)
	y(0)=1	y(0)=1
	x [0; π]
30	1	x2 y'+xy +1 = 0
	y'= y x	y(1)=2
	y(0)=2
	x [0; 1]

Таблица № 5.2: Варианты лабораторной работы № 5 «Методы решения дифференциальных уравнений».

№	Неоднородное ДУ
вар.	второго порядка
1	2
1	y''−5y'+6 y = 2 cos(x)
	y(0)=3
	y’(0)=1/2
2	y''−2y'+5y = x2 +1
	y(0)=-3
	y’(0)=-1/5
1	2
3	y''−4y'+4y = −x2 +3x
	y(0)=3
	y’(0)=4/3
4	y''+2 y'+10 y = −sin(2x)
	y(0)=0

58

	y’(0)=3/4
5	y''−4y'+3y = e5x
	y(0)=3
	y’(0)=9
6	y''+4 y = sin(2x) +1
	y(0)=1/4
	y’(0)=0
7	y''+y'= e−x
	y(0)=1
	y’(0)=1
8	y''−6 y'+9 y = 9x2 −12x + 2
	y(0)=1
	y’(0)=3
9	y''+9y = 36e3x
	y(0)=0
	y’(0)=0
10	y''+2 y'−8y = 3sin(x)
	y(0)=-1
	y’(0)=-3/2
11	y''+6y'+13y = 8e−x
	y(0)=2/3
	y’(0)=2
1	2
12	y''−4y'+8y = 8x2 + 4
	y(0)=2
	y’(0)=3
13	y''+y'−5y = 50 cos(x)
	y(0)=3

59

	y’(0)=5
14	y''+2y'+5y =13e2x
	y(0)=1
	y’(0)=4
15	y''−4 y'+5y =10x
	y(0)=10
	y’(0)=6
16	y''−4y'+4y = 3x − x2
	y(0)=3
	y’(0)=4/3
17	y''−6y'+9y = 4ex
	y(0)=3
	y’(0)=8
18	y''−4 y'+4 y = −169 sin(3x)
	y(0)=-12
	y’(0)=16
19	y''+2 y'−8y =16x + 4
	y(0)=2
	y’(0)=6
20	y''−4y'+5y = 5x2 − 4
	y(0)=2/25
	y’(0)=3/5
1	2
21	y''−2y'+y = e2 x
	y(0)=3
	y’(0)=1
22	y''+3y'+2 y = sin(2x) + 2 cos(2x)
	y(0)=1

60