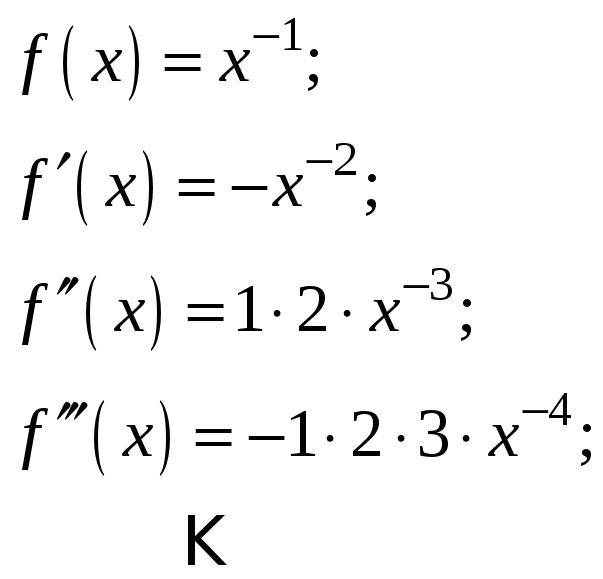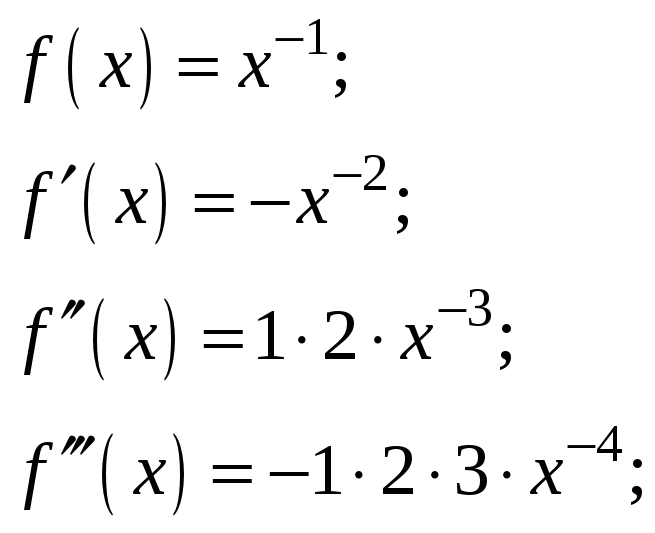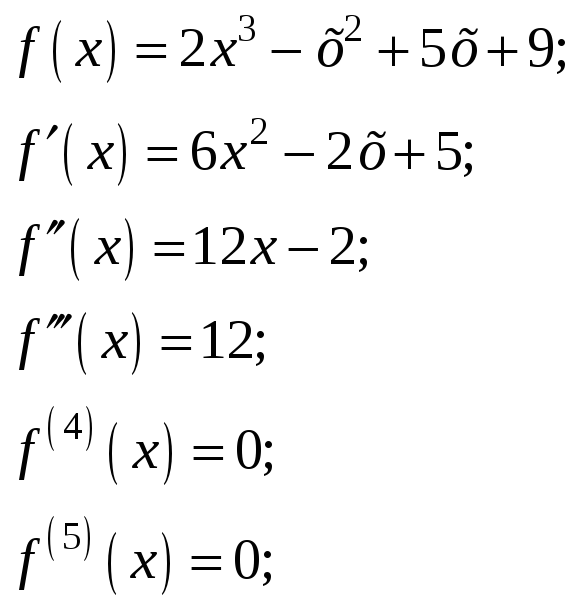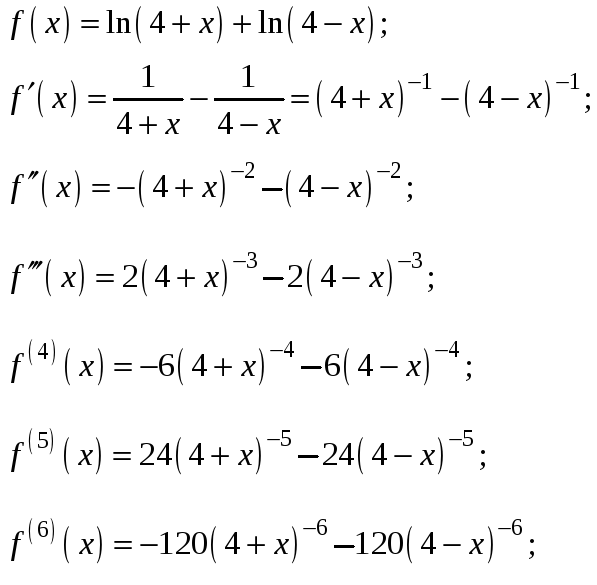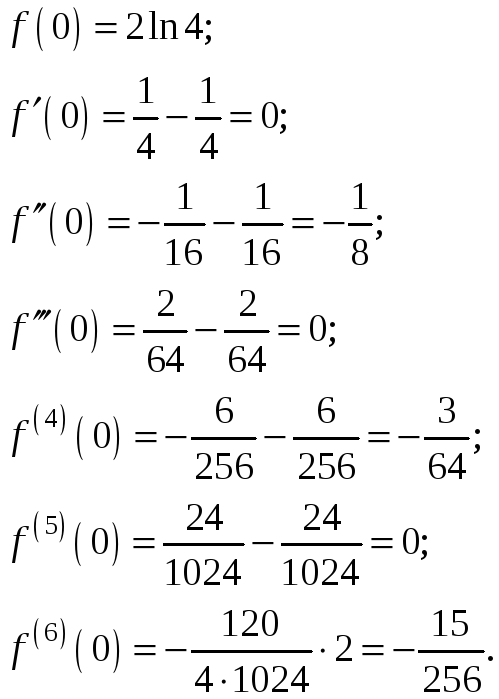мат.анализ_23пс / ОКИШЕВ МатАн ТПС / СЕМЕСТР3 группа 22т / Справочник ФРЯ студ / Справочник задачи / Справочник задачи ТМ

3. ПРИМЕРЫ РАЗЛОЖЕНИЙ В РЯД ТЕЙЛОРА С ПОМОЩЬЮ

ДИФФЕРЕНЦИРОВАНИЯ ИСХОДНОЙ ФУНКЦИИ

В первой задаче покажем как разложение функции f(x) в ряд Тейлора, так и упрощенную аппроксимацию f(x) многочленом Тейлора, содержащим четыре члена. В остальных задачах будем получать только аппроксимации вида при .

З а д а ч а 1 а. Разложить функцию в ряд Тейлора в окрестности точки .

Решение. Удобно проводить нахождение производных и вычисление их значений в точке параллельно, оформляя вычисления в виде двух столбиков. Функцию f(x) представим в более удобном для дифференцирования виде: . Имеем:

Так как главной задачей является получение общей формулы , то сомножители в левом столбике преднамеренно не перемножались, а степени двойки в знаменателях правого столбика преднамеренно не вычислялись. Это облегчает «угадывание» общих формул:

В формуле, полученной для , запись означает чередование знака, но в формуле для за счет подстановки все производные получаются со знаком минус. Этот общий минус выносим за знак суммирования. Составляем ряд Тейлора для функции f(x) в точке :

.

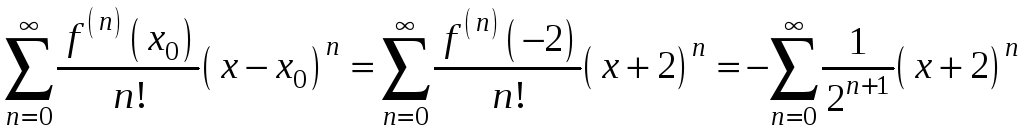Находим радиус и интервал сходимости полученного степенного ряда. Для этого воспользуемся формулой Даламбера для радиуса сходимости, предложенной в методическом издании. Выписываем два последовательных коэффициента ряда Тейлора: . Тогда по формуле Даламбера получаем:

.

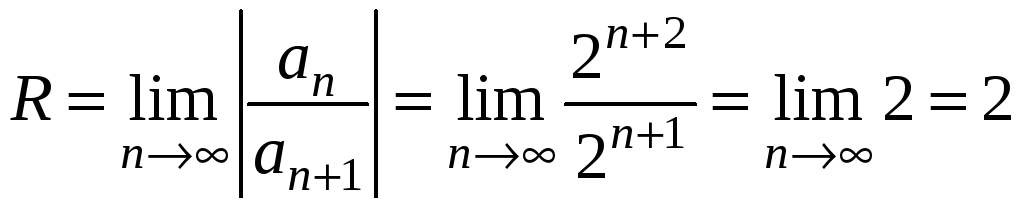Интервал сходимости ряда имеет вид: . В рассматриваемом случае , , поэтому или (в другой форме записи множества) .

В области D ряд Тейлора, составленный по функции , сходится абсолютно, но сходится ли он к породившей его функции? Да, сходится, потому что функция f(x) элементарная и во всех точках D при . Задача решена. Разложение получено.

Ответ: 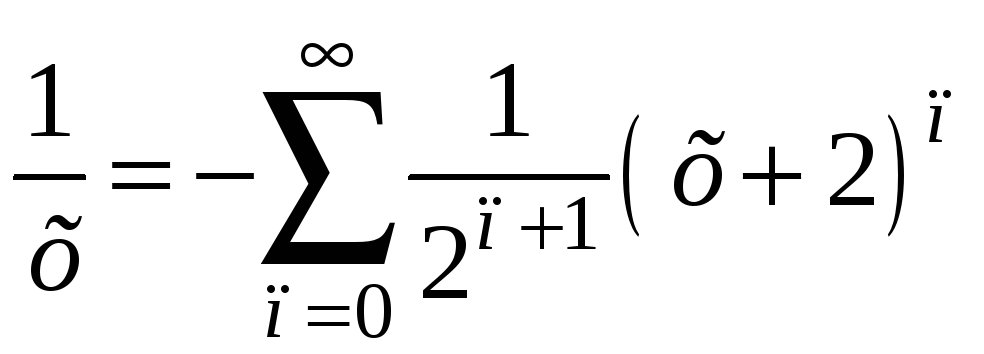при .

Теперь решим для той же самой функции задачу из типового расчета: найдем аппроксимацию функции в окрестности точки .

З а д а ч а 1 б. Найти четыре первых не равных нулю члена разложения функции в ряд Тейлора в окрестности точки .

Решение. Находим, как и в первом варианте решения, значения производных . Для построения аппроксимации необходимо «набрать» четыре ненулевых производных. Имеем:

Первые четыре производных f(x) в точке оказались отличны от нуля, и процесс получения числовых данных завершен. К сожалению, во многих других задачах часть производных зануляется и приходится вычислять большее количество производных.

Выписываем для функции f(x) аппроксимацию вида (16), пользуясь разложением в ряд Тейлора:

.

Полученная аппроксимация функции многочленом Тейлора третьей степени справедлива в малой окрестности точки радиуса . Величина зависит от требуемой точности аппроксимации и может быть найдена с помощью анализа остаточного члена формулы Тейлора. При решении задач типового расчета мы этот анализ проводить не будем, поэтому в ответе конкретная величина не указывается.

Ответ: при .

З а д а ч а 2. Найти четыре первых ненулевых члена разложения функции в ряд Тейлора в окрестности точки . Указать область, в которой применима полученная аппроксимация функции f(x).

Решение. Для применения формулы ряда Тейлора найдем несколько первых производных функции f(x):

Оказывается, что производные функции f(x), начиная с четвертого порядка, зануляются, и поэтому общая формула коэффициента ряда Тейлора имеет вид: 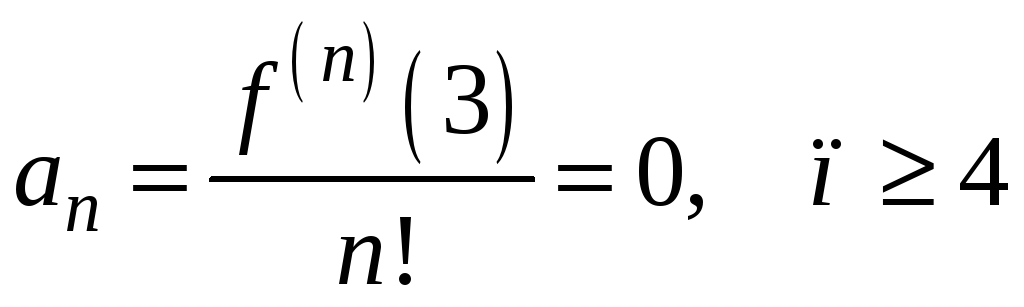. Вместо бесконечного ряда получаем многочлен третьей степени по степеням :

.

Все члены ряда Тейлора, начиная с п = 4, пропали из-за зануления . По сути дела, имеем новую форму записи исходного многочлена f(x). Если раскрыть скобки и привести подобные в , то вновь получим выражение . Поэтому равенство справедливо для всех R и является точным.

Ответ: при R.

Иногда для упрощения дифференцирования функции f(x) полезно преобразовать ее исходную формулу. Рассмотрим следующий пример.

З а д а ч а 3. Найти четыре первых ненулевых члена разложения функции в ряд Маклорена ().

Решение. Преобразуем функцию f(x), воспользовавшись свойством – логарифм произведения равен сумме логарифмов:

. Далее получаем четыре первых ненулевых производных :

Так как производные нечетного порядка в точке зануляются, пришлось проводить вычисления до шестой производной включительно. Само разложение в ряд Маклорена функции является неполным степенным рядом по четным степеням х, что соответствует свойству четности этой функции. Требуемая аппроксимация из четырех первых ненулевых членов ряда Маклорена имеет вид:

.

Ответ: при .

4. ПРИМЕРЫ РАЗЛОЖЕНИЙ ФУНКЦИЙ В РЯД ТЕЙЛОРА

КОМБИНИРОВАНИЕМ ИЗВЕСТНЫХ РЯДОВ

З а д а ч а 4 (простейшая).

Разложить функцию в ряд Маклорена, применяя таблицу известных разложений (алгоритм А2). Выписать общий вид ряда и пять его первых членов.

Решение. Функция f(x) состоит из двух компонент-слагаемых и . Функция является многочленом и уже «разложена» в ряд Маклорена, в котором все коэффициенты, кроме одного, нулевые: . Функцию раскладываем в ряд Маклорена, применяя табличное разложение для (см. прил. 1) и линейную замену независимой переменной у = 3х: ; .

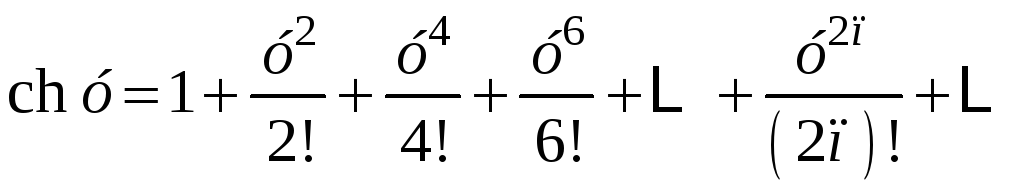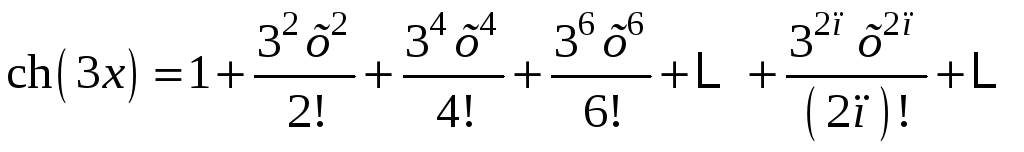Далее, , поэтому производим почленное (по одинаковым степеням х) сложение рядов Маклорена для и . При этом два первых члена ряда выписываем отдельно, так как во втором члене общая формула нарушается за счет прибавления . Для членов ряда с п = 2 сохраняется общая формула членов разложения . Имеем:

.

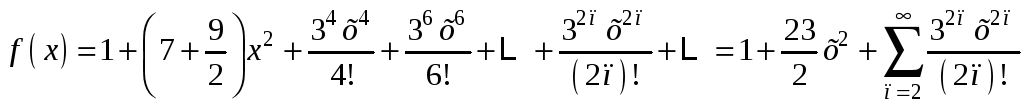Области сходимости для и R, поэтому область сходимости ряда для функции f(x) R, а полученное разложение верно для всех R в силу элементарности функции f(x). Пять первых членов ряда выпишем в ответе.

Ответ: При R верно разложение:

З а д а ч а 5. Разложить функцию 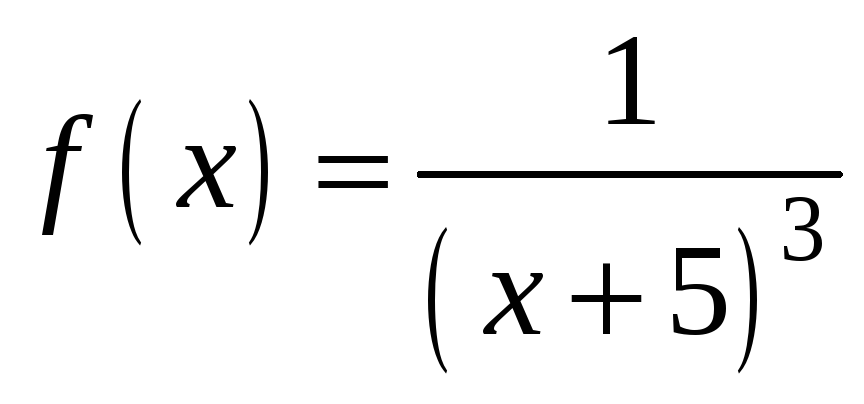в ряд Тейлора с помощью преобразования табличного ряда Маклорена. Применить замену переменной. Выполнить разложения справа и слева от точки разрыва функции f(x). Обосновать интервалы, в которых справедливы найденные разложения.

Решение. Точкой разрыва функции f(x) является . Для разложения f(x) применим биномиальный ряд для функции при . Замена переменной определится положением точки относительно точки разрыва . В общем случае расстояние от точки разрыва до центра разложения равно радиусу сходимости получаемого ряда, т. е.

. (4)

Будем применять только простейшие замены переменной, дающие R = 1.

Разложение функции f(x) справа от ее точки разрыва. Преобразуем выражение f(x):

.

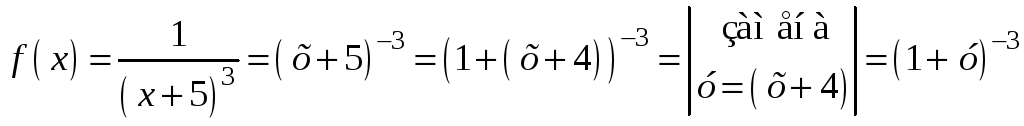Функцию раскладываем в ряд Маклорена с помощью биномиального разложения:

.

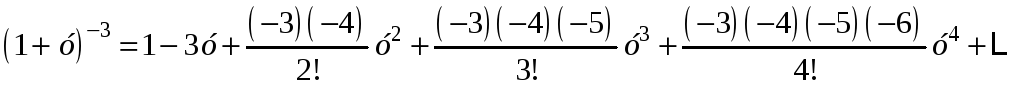Домножим числители и знаменатели дробей на 2 с целью получения в числителях факториалов и выведем общую формулу ряда:

.

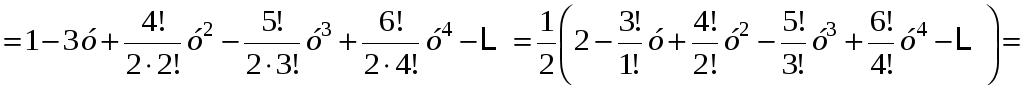
Полученное разложение и аналогичные ему биномиальные разложения можно также найти в приложении. Теперь вернемся к переменной х, получаем:

.

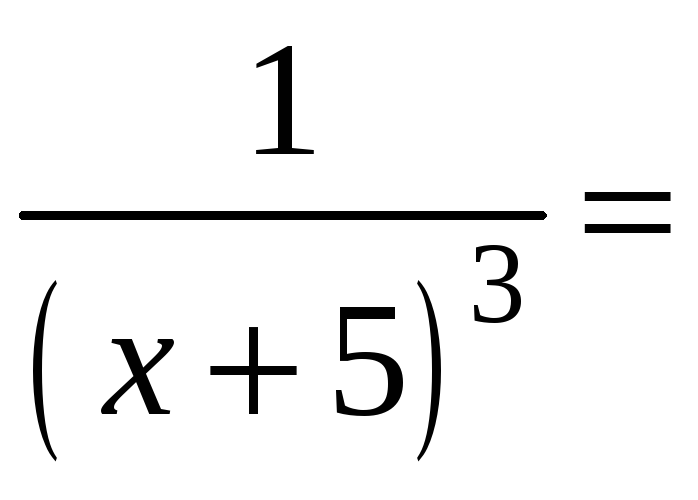
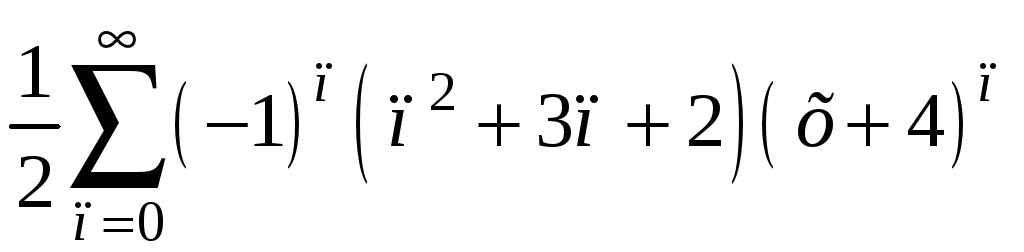Биномиальное разложение верно при , т. е. при , откуда . Как и предполагалось, разложение функции f(x) получилось справа от точки , а радиус сходимости R = 1.

Разложение функции f(x) слева от ее точки разрыва. Преобразуем выражение f(x):

.

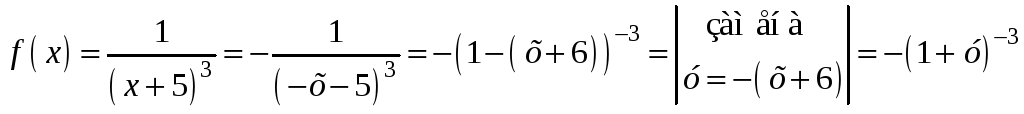Вновь получили биномиальное разложение, но раскладывается в ряд

функция , поэтому

.

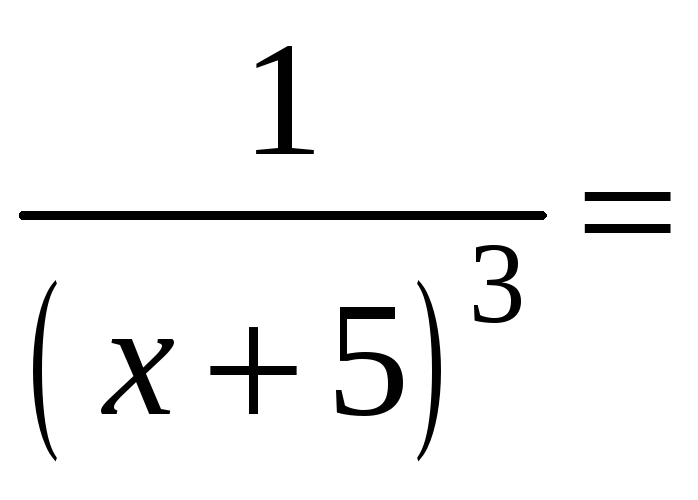
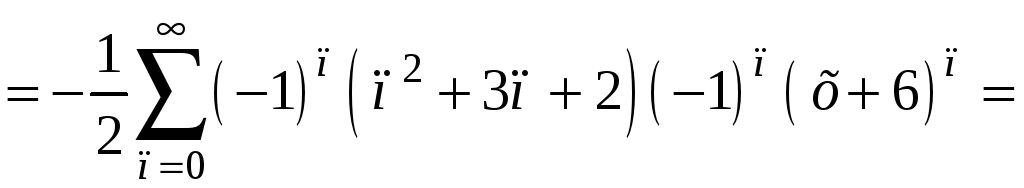
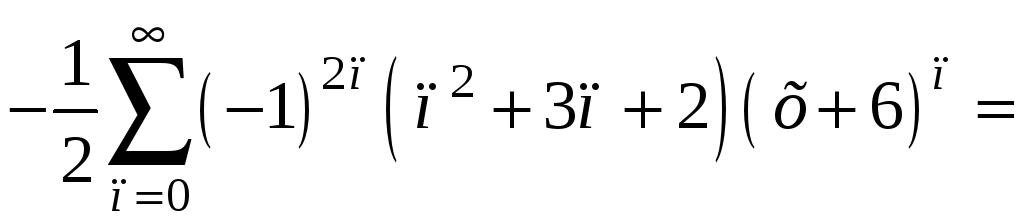
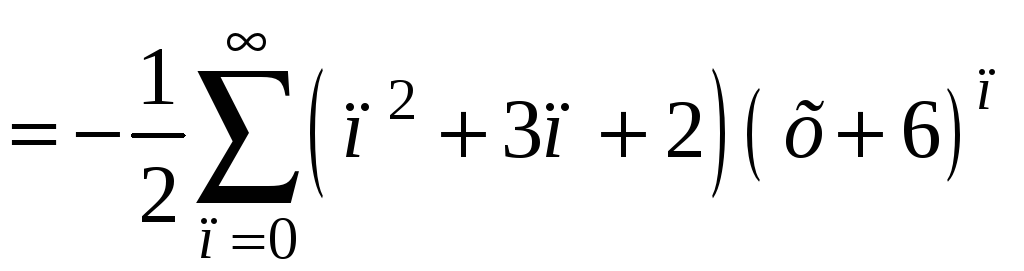Биномиальное разложение верно при , откуда получаем: и . Теперь имеем разложение f(x) слева от точки разрыва и R = 1.

Ответ: Справа от точки разрыва –

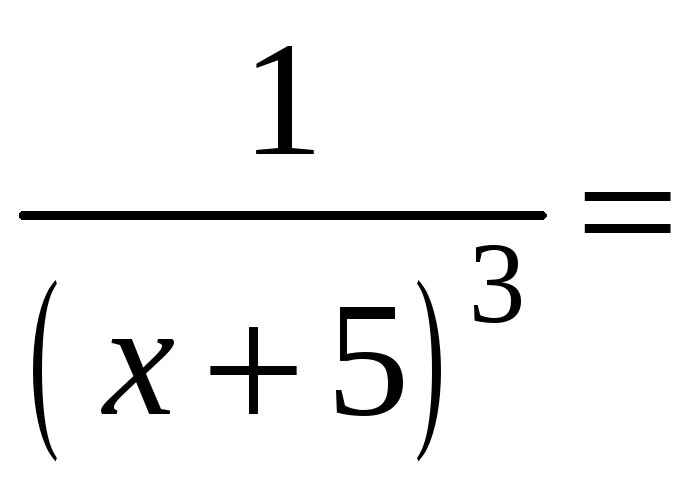
при ;

слева от точки разрыва –

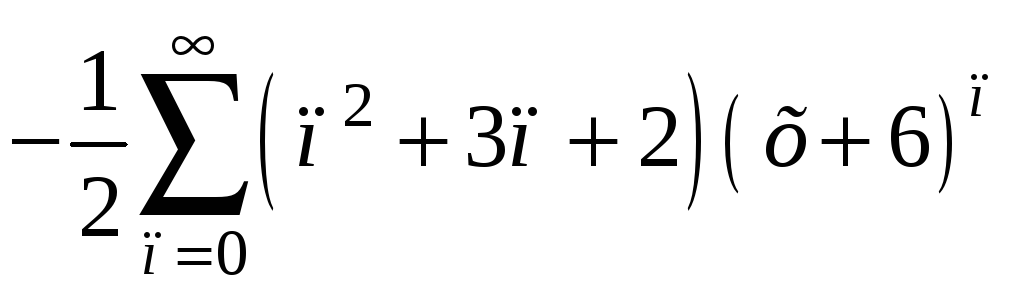при .

З а д а ч а 6. Разложить функцию в ряд Тейлора с помощью преобразования табличного ряда Маклорена. Применить замену переменной. Обосновать интервал, в котором верно найденное разложение.

Решение. Функция определена при x > 3, а сама точка является точкой разрыва второго рода. Очевидно, что функцию f(x) можно разложить в степенной ряд только справа от точки разрыва .

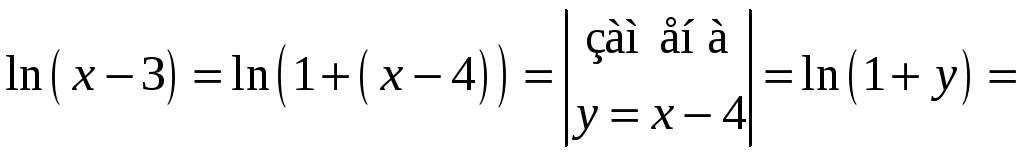
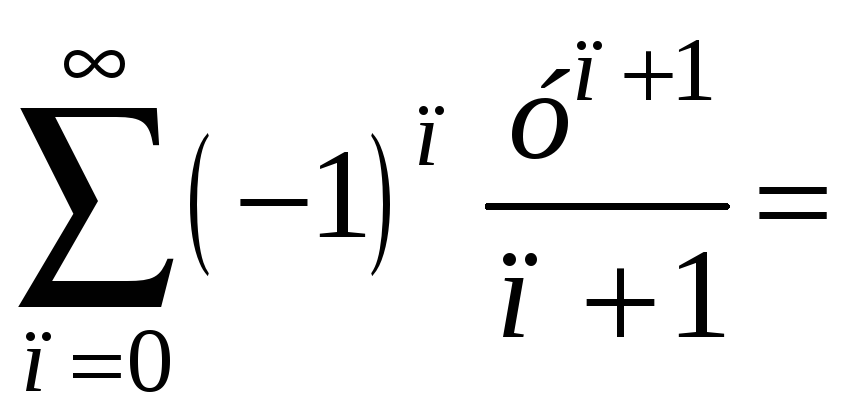
Применяем табличное разложение для и замену переменной, получаем: 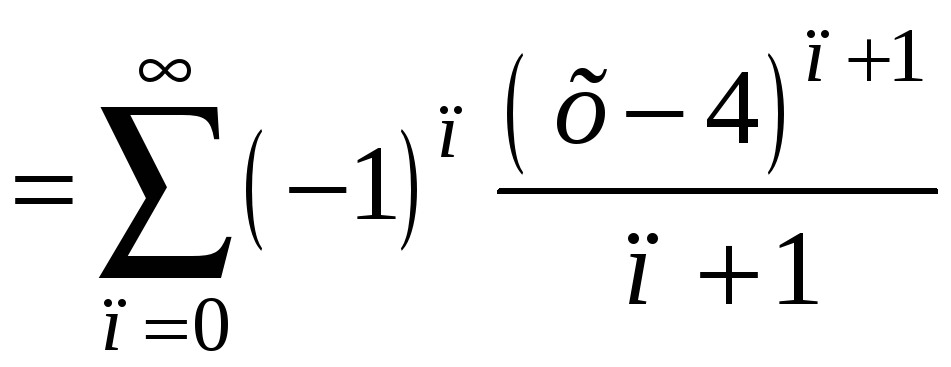. Разложение функции справедливо при . Переходя к переменной х, имеем: или , т. е. получили разложение f(x) справа от точки разрыва и R = 1.

Ответ: 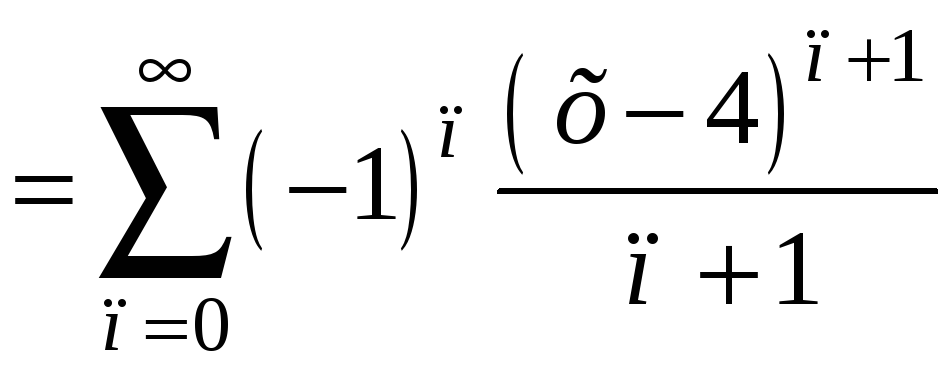при .

З а д а ч а 7. Разложить функцию в ряд Маклорена с помощью комбинирования табличных рядов. Обосновать область, в которой справедливо найденное разложение.

Решение. Функцию f(x) можно представить как произведение двух синусов и попытаться применить операцию умножения двух степенных рядов:

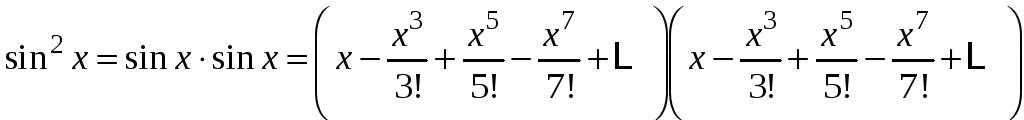, но при перемножении двух рядов получаются столь громоздкие усложняющиеся выражения для коэффициентов ряда, что вывести общую формулу практически невозможно. Удобнее применить формулу понижения степени синуса:

.

Получили выражение f(x) в виде комбинации трех функций: , где ; ; . Первые две функции – это константы, поэтому они являются рядами Маклорена с бесконечными радиусами сходимости . Разложение получается из табличного ряда для заменой у = 2х. После этого выполним действия над степенными рядами (вычитание и умножение) и получим:

.

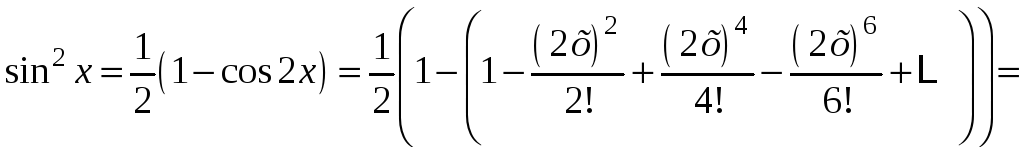
Общая формула (общий член) ряда получается сравнением степеней х и двойки с факториалом и номером члена ряда п.

Ряд для косинуса так же, как и ряды для констант, имеет бесконечный радиус сходимости , поэтому полученное разложение для функции справедливо в области RRR = R.

Ответ: 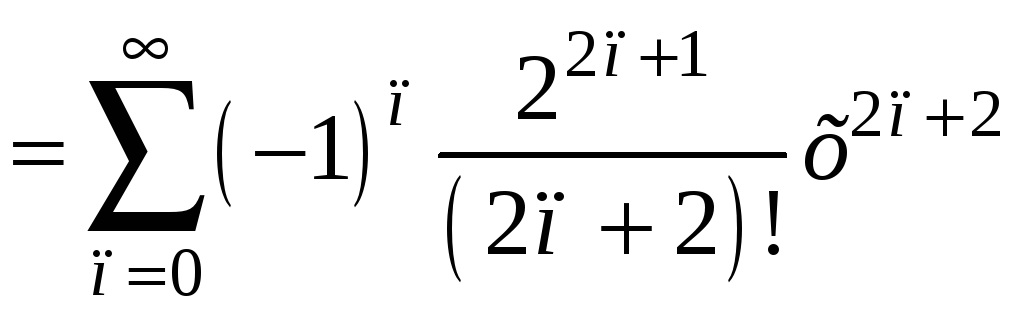при R.

З а д а ч а 8. Разложить функцию 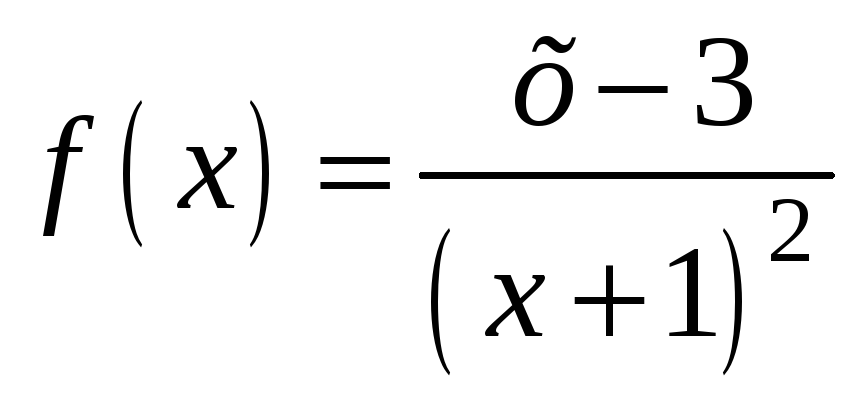в ряд Маклорена с помощью алгоритма А2. Найти область, в которой справедливо полученное разложение.

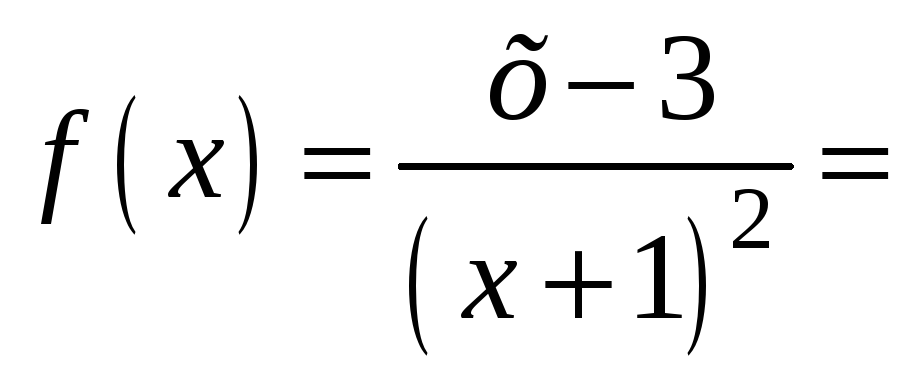
Решение. Представим f(x) как комбинацию функций: . Функция является многочленом, и ее разложение в ряд Маклорена имеет вид: ; R.

Функция раскладывается в биномиальный ряд ():

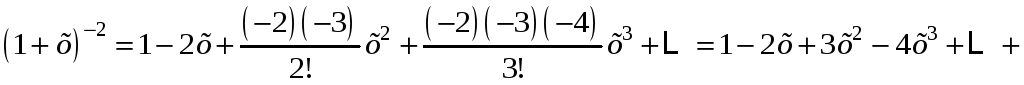
; . Затем выполняется умножение степенных рядов функций и , причем во втором разложении следует «запасти» побольше слагаемых, чтобы не возникло проблем при выводе общего члена ряда для функции f(x).

Две получаемых при умножении бесконечных суммы располагаются одна под другой по одинаковым степеням х и затем складываются «столбиком»:

.

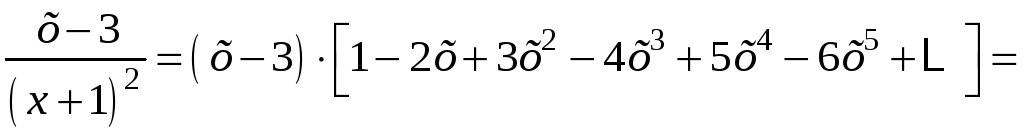
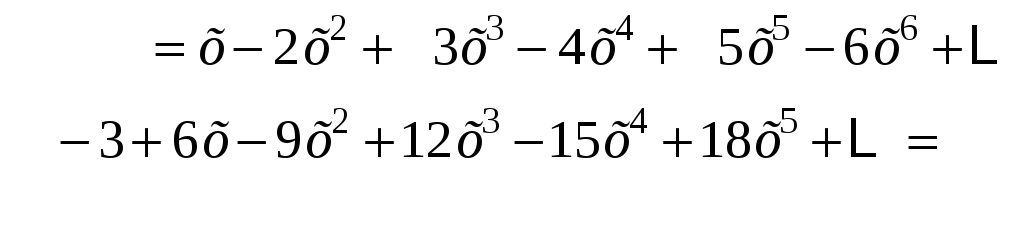
Как видим, коэффициенты полученного ряда имеют чередующийся знак, их модули отличаются между собой на 4, а первый модуль . В результате общая формула коэффициента ряда имеет вид: . Получено разложение функции f(x) в ряд Маклорена: 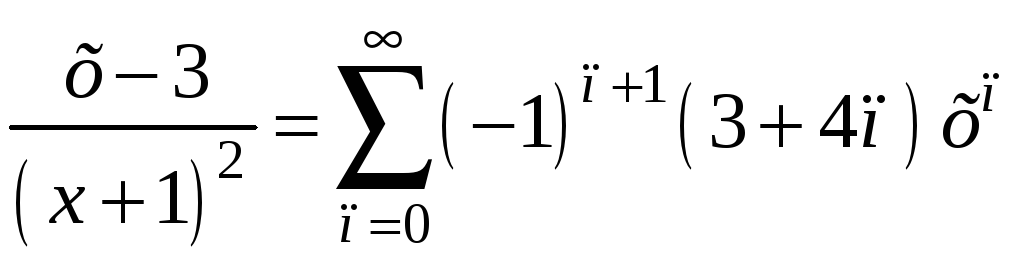. Это разложение справедливо в области R.

Ответ: при .

21