Задача распределения ресурсов

Если финансы, оборудование, сырье и даже людей полагать ресурсами, то значительное число задач в экономике можно рассматривать как задачи распределения ресурсов. Достаточно часто математической моделью таких задач является задача линейного программирования.

Рассмотрим следующий пример.

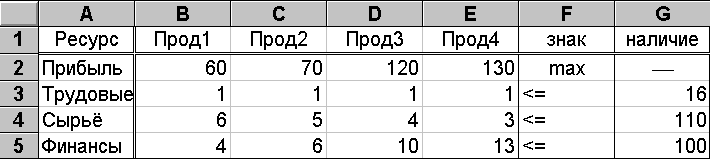Требуется определить, в каком количестве надо выпускать продукцию четырех типов Прод1, Прод2, ПродЗ, Прод4, для изготовления которой требуются ресурсы трех видов: трудовые, сырье, финансы. Количество ресурса каждого вида, необходимое для выпуска единицы продукции данного типа, называется нормой расхода. Нормы расхода, а также прибыль, получаемая от реализации единицы каждого типа продукции, приведены на рис. 6. Там же приведено наличие располагаемого ресурса.

Рис. 6.

Составим математическую модель, для чего введем следующие обозначения:

— количество выпускаемой продукцииj-го типа,;

— количество располагаемого ресурса i-roвида,;

— норма расходаi-ro ресурса для выпуска единицы продукцииj-го типа;

— прибыль, получаемая от реализации единицы продукцииj-го типа.

Теперь приступим к составлению модели.

Как видно из рис. 6, для выпуска единицы Прод1 требуется 6 единиц сырья, значит, для выпуска всей продукции Прод1 требуется 61 единиц сырья, где x_i— количество выпускаемой продукции Прод1. С учетом того, что для других видов продукции зависимости аналогичны, ограничение по сырью будет иметь вид:

6х₁+5х₂+4х₃+3х₄< 110.

В этом ограничении левая часть равна величине потребного ресурса, а правая показывает количествоимеющегосяресурса.

Аналогично можно составить ограничения для остальных ре­сурсов и написать зависимость для целевой функции. Тогда математическая модель задачи будет иметь вид:

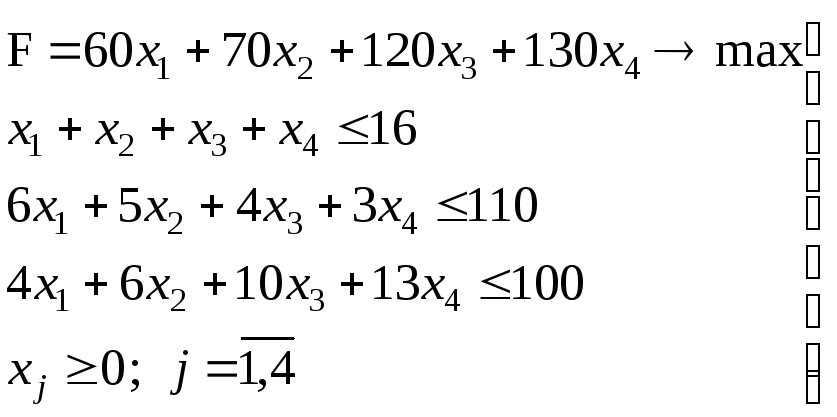(8)

Задачу, имеющую 4 переменных, представить на плоскости, как мы уже знаем, невозможно, поэтому познакомимся с аналитическим методом решения таких задач.

Основные положения симплекс-метода

Для решения рассматриваемой задачи вернемся к теории.

Идея аналитического решения таких задач заключается, как мы уже говорили, в последовательном переборе вершин, в одной из которых и находится оптимальное решение.

Для аналитического решения задач линейного программирования разработан специальный алгоритм направленного перебора вершин. Этот алгоритм обеспечивает переход от одной вершины к другой в таком направлении, при котором значение целевой функции от вершины к вершине улучшается.

В геометрии есть такое понятие "симплекс". Симплексом тела в k-мерном пространстве называют совокупность k+lего вершин. Так, для плоскости приk= 2 симплексом будут три вершины треугольника, приk= 3— четыре вершины четырехгранника и т. д. С учетом этого понятия аналитический метод решения задачи линейного программирования называютсимплекс-методом.Вычисления, обеспечивающие определение значения целевой функции и переменных в одной вершине, называются итерацией.

Аналитическое решение задачи линейного программирования — дело весьма сложное, поэтому подробно описывать его не будем, а изложим лишь те его основные идеи, которые реализованы в Excel.

Решение задачи с помощью симплекс-метода будем рассматривать на примере задачи, математическая модель которой имеет вид (8).

По сравнению с системой (8) в системе (9) введены дополнительные переменные y_iи выполнен переход от системы неравенств к системе уравнений. Следует подчеркнуть, что с точки зрения содержания величинау; равна величине неиспользованного ресурса.

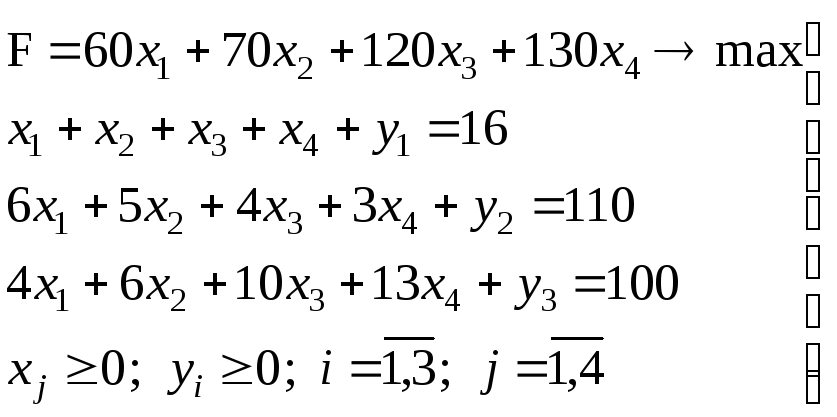(9)

Систему (3.1.9) перепишем в следующем виде:

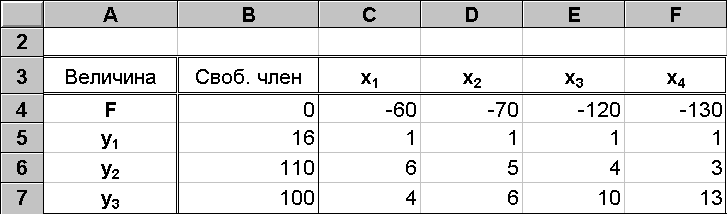
(10)

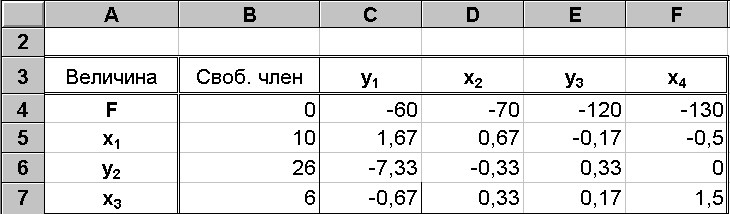
Систему (10) можно представить в виде таблицы, приведенной на рис. 7.

Рис. 7

Таблица (рис. 7) называется симплекс-таблицей и является основной формой решения задачи линейного программирования. В этой таблице все переменные делятся на свободные и базисные. Свободныепеременные находятся в ячейках C3:F3, базисные— в ячейках А5:А7. Если переменная свободная, то ее значение равно нулю. На рис. 7 все основные переменные свободные, следовательно,

x₁ = x₂ = x₃ = x₄ = 0.

Значения базисных переменных приведены в ячейках В5:В7, следовательно,

y₁=16;у₂= 110;у₃= 100.

Действительно, если x₁=x₂=х₃=x₄= 0, т.е. продукция не выпускается, то величинаунеиспользованного ресурса будет равна всему имеющемуся ресурсу, и прибыль при этом, естественно, будет равна0(В4 = 0).

Как мы знаем, решения бывают допустимыми и оптимальны­ми. Каждое решение имеет свой признак. Приведем (без дока­зательства, достаточно сложного) эти очень важные признаки, которые нам потребуются в дальнейшем.

Признак 1

Признак 1 определяет, является ли полученное решение допустимым.Согласно этому признаку решение является допустимым,если в столбце свободных членовВ5:В7 (целевая функция не рассматривается)все величины неотрицательные.

Признак 2

Признак 2 определяет наличие оптимального решения, при этом возможны 2 варианта:

• Признак 2а

Целевая функция имеет минимальноезначение в том случае, когда все элементы в строке целевой функции C4:F4 (свободный член не рассматривается) будутотрицательными.Следовательно, на рис. 7 приведено решение при минимизации целевой функции. Действительно, если ничего не выпускать, то

x₁=x₂= х₃=x₄=0,

и при этом прибыль будет F = В4 = 0.

• Признак 2б

Целевая функция имеет максимальноезначение в том случае, когда все элементы в строке целевой функции C4:F4 будутположительными.

Поскольку таблица на рис. 7 не удовлетворяет признаку максимизации целевой функции, что нам требуется найти в решаемой задаче, то приступим к ее решению с помощью симплекс-метода.

Как мы говорили, поиск оптимального решения заключается в переборе вершин ОДР. При этом переход от одной вершины к другой производится по достаточно сложному алгоритму симплекс-метода, который заключается в обмене переменных. Каждый переход от одной вершины к другой, который, как мы знаем, называется итерацией, состоит в том, что одна базисная переменная приравнивается к нулю, т. е. переходит в свободную, а одна свободная переменная переводится в базисную. На каждой итерации проверяют удовлетворение признаков допустимого и оптимального решений. Такая процедура продолжается до тех пор, пока не будут удовлетворены оба признака. Применительно к нашей задаче последняя симплекс-таблица, полученная после второй итерации, будет иметь вид, приведенный на рис. 8.

Рис. 8

Из этой таблицы видно, что в столбце свободных членов все элементы положительные, тогда по признаку 1 решение является допустимым.В строке целевой функции все элементы также положительные. Следовательно, согласнопризнаку 2б решение является оптимальнымв смысле максимизации целевой функции. В этом случае оптимальным решением будут величины:

,(которые являются базисными);

(так как они свободные);

целевая функция F=1320.

Таков результат решения задачи. Но это еще не все. Симплекс-таблица является мощным средством для выполнения анализа.

Посмотрим, что еще можно узнать из симплекс-таблицы. На рис. 8 видно, что свободные переменные y₁=у₃= 0, а базисная переменная y₂= 26. Это значит, что в оптимальном плане величины неиспользованных трудовых и финансовых ресурсов равны нулю. Следовательно, эти ресурсы используются полностью. Вместе с тем, величина неиспользованных ресурсов для сырьяу₂= 26, значит, имеются излишки сырья. Вот какие выводы можно сделать с помощью симплекс-таблицы.

И это тоже, оказывается, еще не все. Но об этом чуть позже.