8. Цепи с распределенными параметрами

8.1. Задача анализа цепей с распределёнными параметрами. Дифференциальное уравнение длинной линии

Цепями с распределенными параметрами называются идеализированные электрические цепи, процессы в которых описываются дифференциальными уравнениями в частных производных. Токи и напряжения в одномерной цепи с распределенными параметрами являются функциями двух переменных - времени tи координатыx.

Исторически сложилось так, что первыми в качестве одномерных цепей с распределенными параметрами стали представлять так называемые длинные цепи, т.е. линии передачи энергии от источника к нагрузке, длина которых значительно превышает длину волны передаваемых электромагнитных колебаний. Поэтому одномерные цепи с распределенными параметрами часто называют длинными линиями или линиями.

Рассматривая электромагнитные процессы, происходящие в электрических линиях, при помощи которых электрическая энергия или сигналы передаются на расстояние, необходимо иметь в виду, что магнитное и электрическое поля распределены по всей длине линии и превращение электромагнитной энергии в тепло также происходит по всей длине линии.

Если мысленно выделить какой-либо конечный участок этой линии, то токи на концах этого участка окажутся неодинаковыми вследствие наличия токов смещения, обусловленных емкостью между токоведущими проводниками, и токов утечки через изоляцию. Только при бесконечном уменьшении участков линии токи на концах их можно считать равными друг другу.

Магнитный поток, который сцепляется с контуром тока, образуемым токоведущими проводниками, определяет индуктивность цепи.

Емкость между проводами, а также емкости этих проводов по отношению к земле (или соответственно к корпусу машины, самолета, корабля и т. д.) и другим соседним проводам определяют емкость цепи.

Тепловые потери в проводах с учетом поверхностного эффекта и эффекта близости обусловливают продольное активное сопротивление цепи

Наконец, несовершенство изоляция (проводимость изоляции и диэлектрические потери, возникающие в ней определяет поперечную активную проводимость цепи.

В качестве цепи с распределенными параметрами ниже рассматриваетсяоднородная двухпроводная линия, т. е. такая линия, индуктивность, емкость, активное сопротивление и проводимость которой равномерно распределены вдоль всей длины линии. Эти электрические параметры, отнесенные к единице длины линии, называютсяпервичными параметрамилинии; они обозначаются через L₀, С₀,R₀иG₀. Первичные параметры линии зависят от её конструкции и частоты.

В зависимости от того, какие процессы в исследуемой реальной цепи имеют преобладающий характер, а также от степени идеализации, эквивалентная схема элементарного участка цепи может не содержать тех или иных из показанных на рис. 8.1 элементов. В соответствии с этим цепи с распределенными параметрами подразделяют на цепи без потерь (LC-линии), резистивно-емкостные (RC- линии), резистивно-индуктивные (RL- линии) и резистивные (RG- линии). Наиболее интересны процессы в линиях без потерь и в линиях общего вида с малыми потерями, которые используются в основном для моделирования реальных линий передачи и колебательных систем сверхвысоких частот. С развитием микроэлектроники возрос интерес к исследованию процессов вRC-линиях, которые используют в качестве моделей различных пассивных элементов интегральных микросхем (пленочных и диффузионных резисторов, конденсаторов, соединительных проводников и перемычек), а также к исследованию резистивных линий, которые применяют для моделирования контактов к различным микроэлектронным элементам.

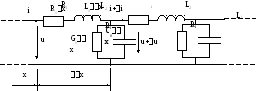
Рис. 8.1. Элементарный участок цепи с равномерно распределёнными параметрами

Напряжение и ток в линии являются функциями двух независимых переменных: пространственной координаты х, определяющей место наблюдения, и времениt,определяющего момент наблюдения. Здесь предполагается, что направление координатной осихсовпадает с направлением оси линии.

Нашей задачей является нахождение пространственно-временного распределения тока в линии i(x, t) и напряжения между проводамии (х, t).Выберем положительное направление тока в линии слева направо (рис. 8.1)и условимся называть «началом» линии левый конец, а «концом» линии —правый конец. Расстояние до произвольной точки линии от начала обозначим черезх,а от конца —черезy.

Выделим элементарный участок линии длиной x,находящийся на расстояниихот начала. Пользуясь первичными параметрамиr,g, LиС,отнесенными к единице длины, приближённо представим рассматриваемый участок в виде последовательно включённых сопротивленияR₀xи индуктивностиL₀xи параллельно включённых активной проводимостиG₀xи ёмкостиC₀x. Обозначим:

и —напряжение между верхним и нижним проводами в точкех,

u+u —приращение напряжения на участкеx,

i —ток в точкех,

i+I —приращение тока на участкеx.

Уравнения для приращений напряжений и тока на элементе длиныxзапишутся следующим образом:

(8.1)

Ввиду наличия двух независимых переменных (x иt) уравнения записываются в частных производных.

По мере стремления xк нулю степень точности этих уравнений повышается.

Итак, линия рассматривается как цепная схема с бесконечно большим числом звеньев, электрические параметры которых бесконечно малы.

Разделив обе части уравнений (8.1)наxи перейдя к пределуx= 0,получаем дифференциальные уравнения

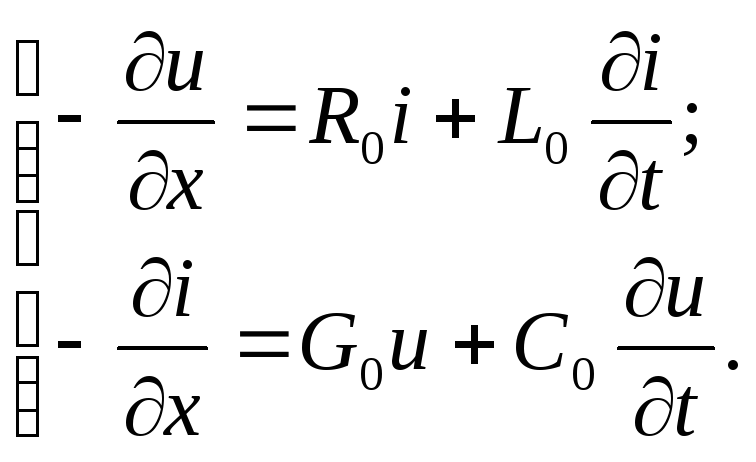(8.2)

Эти уравнения известны в литературе под названием телеграфных уравнений.

Если за начало отсчета принять конец линии, т. е. ввести координату y,то уравнения примут вид:

(8.3)

Уравнения (8.2)или (8.3)могут быть решены однозначно при использовании начальных и граничных условий.Начальными условиямибудут значения напряжения и тока в начале или конце линии в момент времени, принятый за нуль.Граничные условияопределяются связями между напряжением и током в начале или конце линии, зависящими от заданного режима работы линии.

Решение указанных выше уравнений дает функциональные зависимости напряжения и тока в линии от переменных х(илиy)иt.

Для решения дифференциальных уравнений линии воспользуемся операторным методом, который позволяет перейти от решения дифференциальных уравнений в частных производных для мгновенных значений токов i = i(x, t)и напряженийu = u(x, t)линии к решению обыкновенных дифференциальных уравнений, составленных относительно операторных изображений соответствующих токов и напряжений.

Применив преобразование Лапласа к уравнениям (8.2), получаем

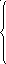
(8.4)

где функции u(x, 0), i(x, 0)описывают распределение напряжения и тока вдоль линии приt = 0, т.е. определяют начальные условия задачи. В связи с тем что в уравнениях (8.4) содержатся производные неизвестных функцийU(x, p) иI(x, 0)только по одной переменной, частные производные этих функций поxзаменены обыкновенными (полными) производными.

При нулевых начальных условиях уравнения (8.4) принимают вид

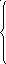
(8.5)

где Z₁(p) = R₀ + pL₀,Y₁(p) = G₀+ pC₀- операторные погонное сопротивление и погонная проводимость линии.

Уравнения (8.5) путем исключения переменных могут быть сведены к одному дифференциальному уравнению, составленному относительно тока или напряжения

(8.6)

- (8.7)

операторный коэффициент распространения.

Таким образом, распределение операторных изображений токов и напряжений в однородной цепи с распределенными параметрами определяется решениями линейного дифференциального уравнения второго порядка с постоянными коэффициентами, общее решение которого имеет вид

U(x, p) = A₁(p)e^{- (p) x} + A₂(p)e^{ (p) x}, (8.8)

где A₁(p), A₂(p) - постоянные интегрирования, определяемые граничными условиями задачи, т.е. значениями неизвестных функцийU(x, p)иI(x, p) в начале (x = 0) или в конце (x = l) линии. Подставляя (8.8) в уравнение (8.5), находим выражение для операторного изображения тока линии

I(x, p) = A₁(p)e^{- (p) x}/Z_B(p) - A₂(p)e^{ (p)x}/Z_B(p). (8.9)

Величина Z_B(p)называется операторным волновым сопротивлениемлинии.

(8.10)

Определяя значения постоянных интегрирования, соответствующие тем или иным граничным условиям, и подставляя их в выражения (8.8), (8.9), можно получить операторные изображения тока и напряжения в любом сечении линии при произвольном внешнем воздействии, а также найти любые частотные и временные характеристики исследуемой цепи.