Лекция 6 Геометрические и аффинные преобразования на плоскости.

Методы преобразования, рассматриваемые ниже, являются основным инструментом манипулирования элементами изображений. Понимание принципов изменения и преобразования элементов изображений в значительной мере увеличивают наши возможности при создании изображений средствами машинной графики и адекватное восприятие результатов преобразования.

Соотношения между точками трехмерного евклидового пространства и их координатами, может быть задано либо радиус – вектором

=, гдеe_x, e_y, e_zединичные вектора осей,

либо матрицам вида или.

Геометрические преобразования, проводимые в компьютерной графике как на плоскости, так и в пространстве, возможно проводить в двух вариантах.

Первый подход заключается в том, что рассматривается преобразование одного множество точек в другое, но при этом система координат, в которой определены оба эти множества, остается неизменной, а сам объект преобразуется относительно начала координат до получения желаемого результата.

Другой вариант подхода заключается в преобразовании систем координат. Этот случай обычно полезен, когда желательно собрать вместе много объектов, каждый из которых описан в своей собственной (локальной, пользовательской) системе координат, и выразить координаты всех объектов в одной глобальной (“мировой”) системе координат.¹Переход от одной прямоугольной КС к другой в общем случае описывается следующими соотношениями:

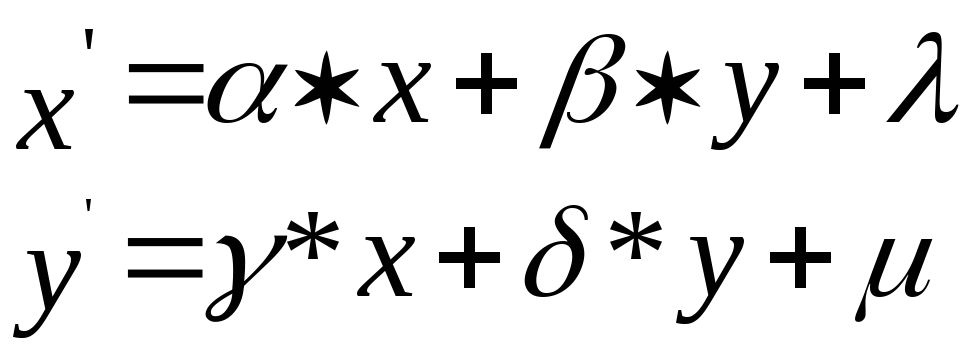, гдеa,b,c,dпроизвольные числа, связанные между собой соотношением:

.

Необходимо отметить, что оба варианта проведения преобразований эквивалентны. Здесь будем рассматривать вариант геометрических преобразований, когда система координат остается неизменной, а точка М(x, y) под действием какого - либо преобразования перемещается в точкуM`(x`, y`), определённой в той же системе координат.

Определим аффинные преобразованиякак преобразования, которые сохраняют прямолинейность прямых линий, параллельность параллельных прямых и деление отрезков в заданных отношениях. В аффинных преобразованиях на плоскости особую роль играют несколько важных случаев, имеющих хорошо прослеживаемые геометрические характеристики. Все изменения над отдельными подмножествами точек изображения и изображением в целом выполняются с помощью четырех базовых операций: перемещения, масштабирования, отражения и поворота, которые лежат в основе многих графических приложений.

Рассмотрим некоторое произвольное графическое изображение, которое описывается множеством из Nточек. Это множество может быть дополнено подмножеством пар точек, которые должны быть соединены прямыми линиями. Каждаяi-я точка представляется на плоскости вектором положения с помощью ее двух координатx_i и y_{i ,} которые можно рассматривать как элементы матрицыA, описывающей изображение, размеромN * 2.

Предположим, что известно другое графическое изображение в той же координатной системе XY, описываемое матрицейB, размеромN * 2. Введем матрицу преобразованияT такую, что

A * T = B, для выполнения подобного преобразования, матрицаTдолжна иметь размерность 2 х 2. Здесь необходимо отметить, что в общем случае, произведение матрицАи Тне коммутативно.T– матрица преобразования, которая позволяет выполнять различные геометрические преобразования над множествами точек, определенных на координатной плоскостиXY. Матричное произведениеA*T- основа математических преобразований, используемых в двухмерной графике:

• вращение, относительно начала координат;

• масштабирование;

• зеркальное (симметричное) отображение;

• перемещение.

О

Рис. 3.25 Поворот точки относительно начала координат

тносительно, последнего преобразования – перемещение, необходимо отметить следующее: - одновременно переместить все точки с помощью матрицыT, в виде определенном выше нельзя, поскольку, например, точка (0,0) после умножении на матрицу T любого вида останется неизменной и в матрицеB.

Рассмотрим кратко механизм этих преобразований. В качестве математической основы преобразований используется механизм алгебры матриц.