
3. На множестве целых чисел z, так же как и на множестве n0 целых неотрицательных чисел, определим бинарное отношение «меньше».
Определение 9. Говорят, что целое число х меньше целого числа у (пишут х < у), если существует такое натуральное число k, что выполняется равенство х + k = у. В символах математической логики определение 9 имеет вид:
(x
< y)
 ($
k
($
k
 N)(x
+ k
= y).
N)(x
+ k
= y).
Если число х меньше числа у, то говорят, что у больше х и пишут у > х. Запись х £ у означает, что х меньше или равняется y (x не больше у), а запись х ³ у, в свою очередь, означает, что х больше или равняется у (х не меньше у).
Теорема
6.
Для любых х,
у
 Z
имеет
место
точно одно
из трех
соотношений: х
<
у;
х = у ; у <
х.
Z
имеет
место
точно одно
из трех
соотношений: х
<
у;
х = у ; у <
х.
Доказательство. Рассмотрим разность х – у. Согласно теореме 4 и определению 6, она может быть числом отрицательным, равным нулю или положительным. Если разность х – у есть число отрицательное, то число – (х – у) = у – х = k является положительным, а значит, по определению 5 разности, х + k = у, то есть х < у.
Если х – у = 0, то очевидно, что х = у.
Если
же х
– у –
положительное число, то можем записать,
что
х
–
у
=
k
,
k
 N.
Но тогда,
по определению
разности, х
= у +
k,
или
х
>
у.
Теорема
доказана.
N.
Но тогда,
по определению
разности, х
= у +
k,
или
х
>
у.
Теорема
доказана.
Как и на множестве целых неотрицательных чисел N0, отношение «меньше» на множестве Z является отношением строгого линейного порядка, а значит, Z – линейно упорядоченное множество.
Кроме того, множество Z бесконечное, так как содержит бесконечное подмножество N0. Легко показать, что Z – дискретное множество, в нем выполнен принцип наибольшего (наименьшего) числа и свойство Архимеда.
Всеми
указанными свойствами обладает и
множество N0
целых неотрицательных
чисел. Однако, в отличие от множества
N0,
множество Z,
не
содержит наименьшего числа. Действительно,
для всякого х
 Z
существует
число х
– 1
Z
существует
число х
– 1
 Z,
которое
будет меньше, чем х.
Z,
которое
будет меньше, чем х.
Итак, множество Z целых чисел обладает следующими свойствами: оно бесконечное, линейно упорядоченное, дискретное, в нем нет наибольшего и наименьшего чисел.
Как уже отмечалось, множество целых чисел Z образует группу относительно операции сложения. Кроме того, по свойствам 3, 4 и 5 операций сложения и умножения, множество Z является коммутативным и ассоциативным кольцом с единицей. Однако множество Z не является полем, поскольку не выполняется условие существования обратного элемента.
Для геометрической интерпретации целых чисел возьмем произвольную прямую l и точку О на ней. Точка О делит прямую на два луча, один из которых назовем положительным (правым), а другой – отрицательным (левым). Выберем произвольный отрезок е и будем считать его единичным отрезком, или единицей длины. От точки О на положительном луче (вправо) отложим отрезок ОА = пе, являющийся суммой п единичных отрезков. Точке А на прямой поставим в соответствие натуральное число п (рис. 1).
А/ О А

– n 0 e n x
Рис. 1
Откладывая
отрезок ОА1
= пе (п
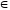 N)
от
точки О
на
отрицательном луче (влево), найдем на
прямой l
точку А',
которой
поставим
в соответствие отрицательное число –п.
Точке
О
поставим
в соответствие
число нуль.
N)
от
точки О
на
отрицательном луче (влево), найдем на
прямой l
точку А',
которой
поставим
в соответствие отрицательное число –п.
Точке
О
поставим
в соответствие
число нуль.
Таким образом,
каждому целому числу х
ставится в соответствие точка М
прямой l,
отстоящая от точки О
на
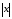 единиц и расположенная на правом луче,
если х
– положительное, и на левом – если х
– отрицательное число.
единиц и расположенная на правом луче,
если х
– положительное, и на левом – если х
– отрицательное число.
Число х, соответствующее точке М, называется координатой этой точки. Тот факт, что точка М имеет координату х, будем записывать в виде М(х).
Изображение целых чисел с помощью точек прямой позволяет задавать не только длины отрезков, но и указывать их направление. Следовательно, геометрически целое число – это направленный отрезок, лежащий на прямой l и выходящий из точки О.

–4 –3 –2 –1 0 1 2 3 4 x
Рис. 2
Вышеуказанные свойства множества целых чисел иллюстрируются на числовой прямой (см. рис. 2).
