
- •Введение.
- •1. Формулировка транспортной задачи.
- •2. Математическая модель транспортной задачи.
- •3. Необходимое и достаточное условия разрешимости транспортной задачи.
- •4. Свойство системы ограничений транспортной задачи.
- •5. Опорное решение транспортной задачи.
- •Метод вычеркивания
- •6. Методы построения начального опорного решения. Метод северо-западного угла.
- •Метод минимальной стоимости.
- •7. Переход от одного опорного решения к другому.
- •Означенный цикл.
- •8. Распределительный метод.
- •9. Метод потенциалов.
- •10. Особенности решения транспортных задач с неправильным балансом.
- •11. Алгоритм решения транспортной задачи методом потенциалов.
- •12. Транспортная задача с ограничениями на пропускную способность.
- •13. Транспортная задача по критерию времени.
- •14. Применение транспортной задачи для решения экономических задач.
- •Постановка транспортной задачи на эвм.
- •Задать начальные значения элементам
- •Найти строку с наибольшим числом
- •Найти наименьший эле-
3. Необходимое и достаточное условия разрешимости транспортной задачи.

Теорема1. Для того чтобы транспортная задача линейного программирования имела решение, необходимо и достаточно, чтобы суммарные запасы поставщиков равнялись суммарным запросам потребителей:
![]() ,
т.е. задача должна быть с правильным
балансом.
,
т.е. задача должна быть с правильным
балансом.
Доказательство.
Необходимость.
Пусть задача
имеет допустимое решение
![]()
![]() ,i=1,2,,…,m,
j=1,2,…,n .
Докажем, что
,i=1,2,,…,m,
j=1,2,…,n .
Докажем, что
![]() .
Подставим
.
Подставим![]() в уравнения системы ограничений
(2), (3), получим
в уравнения системы ограничений
(2), (3), получим![]() ,i=1,2,,…,m,
,i=1,2,,…,m,
![]() ,j=1,2,…,n
. Просуммируем первую и вторую группы
тождеств по отдельности:
,j=1,2,…,n
. Просуммируем первую и вторую группы
тождеств по отдельности:
![]()
![]() и
и![]()
![]() .
Отсюда следует, что задача имеет
правильный баланс
.
Отсюда следует, что задача имеет
правильный баланс![]() .
.
Достаточность.
Пусть задача
имеет правильный баланс
![]() =М.
Докажем, что в этом случае задача имеет
оптимальное решение. Сначала убедимся
в том, что область допустимых решений
задачи – непустое множество. Проверим,
что
=М.
Докажем, что в этом случае задача имеет
оптимальное решение. Сначала убедимся
в том, что область допустимых решений
задачи – непустое множество. Проверим,
что![]() =
=![]() ,i=1,2,,…,m,
j=1,2,…,n
является допустимым решением. Подставим
,i=1,2,,…,m,
j=1,2,…,n
является допустимым решением. Подставим
![]() в левые части уравнений системы
ограничений (2), (3), получим
в левые части уравнений системы
ограничений (2), (3), получим![]()
![]() =
=![]()
![]() =
=![]() М=
М=![]() ,i=1,2,,…,m;
,i=1,2,,…,m;
![]()
![]() =
=![]()
![]() =
=![]() М=
М=![]() ,j=1,2,…,n,
т.е. уравнения обращаются в тождества.
Очевидно, что
,j=1,2,…,n,
т.е. уравнения обращаются в тождества.
Очевидно, что
![]() удовлетворяет и условиям неотрицательности.
удовлетворяет и условиям неотрицательности.
Далее
покажем, что существует оптимальное
решение. Учитывая, что стоимости перевозок
единиц груза ограничены сверху и снизу
![]()
![]() ,где
С иD
– конечные постоянные, можно записать
,где
С иD
– конечные постоянные, можно записать
![]()
![]()
 Следовательно,
целевая функция ограничена на множестве
допустимых решений и, как всякая
непрерывная функция, достигает своего
наименьшего (а также и наибольшего)
значения. Теорема доказана полностью.
Следовательно,
целевая функция ограничена на множестве
допустимых решений и, как всякая
непрерывная функция, достигает своего
наименьшего (а также и наибольшего)
значения. Теорема доказана полностью.
4. Свойство системы ограничений транспортной задачи.
Т еорема2.
Ранг системы – условий транспортной
задачи равен N=m+n-1.
еорема2.
Ранг системы – условий транспортной
задачи равен N=m+n-1.
Доказательство.
Как известно
из линейной алгебры, для нахождения
базиса системы векторов
![]() необходимо составить однородную систему
уравнений
необходимо составить однородную систему
уравнений
![]() .
.
 Эту систему с
помощью преобразований Жордана приводят
к равносильной разрешенной; в базис
включают векторы, соответствующие
разрешенным неизвестным. Ранг системы
векторов равен числу векторов, входящих
в базис, т.е. числу разрешенных неизвестных
этой системы.
Эту систему с
помощью преобразований Жордана приводят
к равносильной разрешенной; в базис
включают векторы, соответствующие
разрешенным неизвестным. Ранг системы
векторов равен числу векторов, входящих
в базис, т.е. числу разрешенных неизвестных
этой системы.
Системе векторов – условий транспортной задачи Aij , i=1,2,,…,m, j=1,2,…,n соответствует однородная система уравнений
![]() ,
,
где
![]() =(0,0,…,0)т
– нулевой
вектор (транспонированный).
=(0,0,…,0)т
– нулевой
вектор (транспонированный).
Запишем матрицу этой системы (она является также матрицей системы ограничений транспортной задачи):
![]()

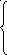


![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Если
к последней строке (уравнению) прибавить
(n-1)
строку (уравнение), начиная с (m+1)-й,
и вычесть первые m
строк, то получится строка, состоящая
из нулей. Это значит, что число разрешенных
неизвестных в этой системе и ранг r
системы векторв-условий не могут быть
равны числу m+n
уравнений. Следовательно, r![]() m+n-1.
m+n-1.
Покажем,
что найдутся N=m+n-1
линейно независимых векторов-условий.
Из векторов-условий задачи выберем
следующие:
![]() - и убедимся, что они линейно независимы.
Для этого составим систему уравнений
- и убедимся, что они линейно независимы.
Для этого составим систему уравнений![]()
![]() .
Матрица этой системы имеет следующий
вид:
.
Матрица этой системы имеет следующий
вид:
![]()
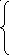
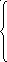






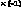

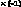


![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() +
+
 С помощью
элементарных преобразований можно
привести ее к единичной. Для этого строки
с (m+1)-й
до (m+n-1)-й
умножим на (-1) и прибавим к первой строке,
тогда в ней останется только одна
единица, остальные элементы будут
нулевыми. После этого первые m
строк умножим на (-1) и прибавим к последней
строке. В результате в матрице останутся
единицы только по диагонали, а последняя
строка будет состоять из нулей.
Следовательно, система уравнений имеет
единственное нулевое решение
С помощью
элементарных преобразований можно
привести ее к единичной. Для этого строки
с (m+1)-й
до (m+n-1)-й
умножим на (-1) и прибавим к первой строке,
тогда в ней останется только одна
единица, остальные элементы будут
нулевыми. После этого первые m
строк умножим на (-1) и прибавим к последней
строке. В результате в матрице останутся
единицы только по диагонали, а последняя
строка будет состоять из нулей.
Следовательно, система уравнений имеет
единственное нулевое решение
![]() ,
а система векторов линейно независима.
Теорема доказана.
,
а система векторов линейно независима.
Теорема доказана.
