Лабораторная работа №3

Применение численных методов для решения простейших задач теплообмена

Цель работы: изучить метод Ньютона для решения нелинейных уравнений и использовать его при решении задачи радиационного теплообмена.

1. Теоретические положения

1.1. Постановка задачи

Пусть требуется рассчитать температуру нагревателя электрической печи сопротивления.

Считаем заданными:

• температуру поверхности нагреваемого металла ;

• степень черноты поверхности нагреваемого металла

• полезную удельную мощность нагревателя ;

• зависимость степени черноты нагревателя от температуры (в интервале 1000-2000 К).

Для решения данной задачи запишем уравнение теплового баланса нагревателя:

, (4.1)

где - плотность потока результирующего излучения на его поверхности.

Выразим через неизвестную температуру , рассматривая поверхности нагревателя и металла как бесконечные параллельные плоскости:

, (4.2)

где - постоянная Стефана - Больцмана.

Подставив выражение (3.2) в уравнение теплового баланса (3.1), получим:

. (4.3)

Зависимость (3.3) представляет собой нелинейное уравнение относительно искомой температуры . Для решения поставленной задачи рассмотрим применение метода Ньютона (метода касательных).

1. Метод Ньютона (метод касательных)

Данный метод предназначен для решения нелинейных уравнений вида: , (4.4)

где функция определена и непрерывна на конечном или бесконечном интервале 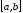. Всякое число , обращающее функцию в нуль, называется корнем уравнения . Пусть корень  уравнения  отделен на отрезке [a, b], причем  и  непрерывны и сохраняют определенные знаки при . Если на некотором произвольном шаге n найдено приближенное значение корня , то можно уточнить это значение по методу Ньютона. Положим

, (4.5)

где  - малая величина.

Применяя формулу Тейлора, получим:

.

Следовательно,

Внеся эту поправку в формулу (3.1), найдем следующее (по порядку) приближение корня:

, (4.6)

Геометрически метод Ньютона эквивалентен замене дуги кривой  касательной, проведенной в некоторой точке кривой (рис. ). Положим для определенности, что  при  и . Выберем, , для которого . Проведем касательную к кривой  в точке B₀ с координатами . В качестве первого приближения  корня возьмем абсциссу точки пересечения касательной с осью Ox.

 

Рисунок

Рис. Геометрическая интерпретация метода Ньютона

Через точку снова проведем касательную, абсцисса точки пересечения которой даст второе приближение корня и т.д. Формулу для уточнения корня можно получить из треугольника , образованного касательной, проведенной в точке B₀, осью абсцисс и перпендикуляром, восстановленным из точки . Тогда . Так как угол  образован касательной и осью абсцисс, его тангенс численно равен величине производной, вычисленной в точке, соответствующей абсциссе точки касания, т.е. и 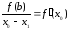. Тогда справедливо, что

(4.7)

или для любого шага n

. (4.8)

В качестве начальной точки  можно принять либо один из концов отрезка [a, b], либо точку внутри этого интервала. В первом случае рекомендуется выбирать ту границу, где выполняется условие

т.е. функция и ее вторая производная в точке  должны быть одного знака.

При использовании метода Ньютона исходное уравнение необходимо привести к виду:

. (4.9)

Тогда в левой части уравнения (4.3) окажется функция:

(4.10)

где - приведенная степень черноты рассматриваемой системы.

Значение уравнения (4.10) при текущем значении называют невязкой уравнения (4.9). На каждом шаге итераций последующему приближению искомой величины соответствует точка пересечения с остью абсцисс касательной к кривой в точке предыдущего приближения. С учетом того, что тангенс угла наклона касательной численно равен производной от невязки исследуемой функции: , получим следующее выражение для :

, (4.11)

т. е. последующее приближение может быть найдено по формуле:

. (4.12)

В общем случае итерационная формула для метода Ньютона имеет вид:

. (4.13)

В процессе расчета по этой формуле значения искомой температуры нагревателя быстро приближаются к решению исходного уравнения, при этом значения невязок стремятся к нулю. Рассмотрим особенности применения метода Ньютона для решения рассматриваемой задачи теплообмена. Отметим, что рассчитывать производную можно достаточно приближено, т. к. ее величина определяет лишь значение очередного приближения, не влияя на окончательный результат расчета. Пренебрегая зависимостью при дифференцировании невязки, получим выражение для приближенного значения производной:

(4.14)

и итерационная формула примет вид:

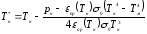. (4.15)

Решение поставленной задачи реализовано в вычислительной среде MathCAD. Расчет по формуле (3.15) приводит к значению искомой величины: 1544,3. Программа, реализующая алгоритм метода Ньютона в системе MathCAD, представлена ниже.

Программа

1. Задаем исходные данные:

Температура поверхности металла:

Степень черноты поверхности нагреваемого металла:

Полезная удельная мощность нагревателя:

Зависимость степени черноты нагревателя от температуры

Отделяем корни уравнения:

2. Определяем неподвижную точку:

_{3. Вычисляем значения итерационной последовательности с использованием рекуррентной формулы метода касательных:}

4. Создаем функцию, реализующую метод касательных

5. Проверяем полученные результаты