Нахождение определителя матрицы по схеме Гаусса Теория метода и алгоритм решения

Пусть

A= (1)

и ∆=detA (2)

Рассмотрим линейную систему Ax=0 (3)

При решении системы (3) по методу Гаусса мы заменяли матрицу А треугольной матрицей В, состоящей из элементов отмеченных строк

B=

В результате получалась эквивалентная система Bx=0 (4)

Элементы матрицы В последовательно получались из элементов матрицы А и дальнейших вспомогательных матриц , ,… ,, с помощью следующих элементарных преобразований:

1. Деления на «ведущие» элементы , , … ,, которые предполагались отличными от нуля

2. Вычитания из строк матрицы А и промежуточных матриц 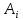( i=1,2, … , n-1 ) чисел, пропорциональных элементам соответствующих ведущих строк. При первой операции определитель матрицы также делится на соответствующий «ведущий» элемент, при второй— определитель матрицы остается неизменным. Поэтому

det B = 1 =

Следовательно,

∆ ==(5)

т. е. определитель равен произведению «ведущих» элементов для соответствующей схемы Гаусса. Отсюда заключаем, что приведенная схема единственного деления , в предыдущем методе, может быть использована для вычисления определителей, причем столбец свободных членов тогда становится излишним.

Заметим, что если для какого-нибудь шага элемент или близок к нулю (что влечет за собой уменьшение точности вычислений), то следует соответствующим образом изменить порядок строк и столбцов матрицы.

Постановка задачи

Найти приближенно определитель матрицы А с точностью до 0,0001 по схеме Гаусса.

Решение

Для удобства поместим вычисления в таблицу

step	а1	а2	а3	а4
1	-1	0,13	-2	-0,14
2	0,75	0,18	-0,21	-0,77
3	0,28	-0,17	0,39	0,48
4	1	3,14	-0,21	-1
1'	1	-0,13	2	0,14
2'	0	0,2775	-1,71	-0,875
3'	0	-0,1336	-0,17	0,4408
4'	0	3,27	-2,21	-1,14
2''		1	-6,16216	-3,15315
3''		0	-0,99326	0,019539
4''		0	17,94027	9,170811
3'''			1	-0,01967
4'''			0	9,523718
∆=	2,625032

Метод итераций (метод последовательных приближений) Теория метода и алгоритм решения

Пусть дана система n линейных уравнений с n неизвестными:

(1),

или в матричном виде: А · х = В (2), где:

А=(),.

, .

Предполагая, что диагональные элементы 0,разрешим первое уравнение системы (1) относительно, второе – относительнои т.д. Получим:

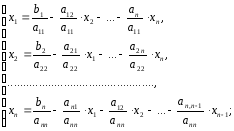(2),

или: (3),

где:

Система (3) называется системой, приведенной к нормальному виду.

Введя обозначения:

, ,

запишем систему (3) в матричной форме: , или:

(4).

Решим систему (4) методом последовательных приближений. За нулевое приближение примем столбец свободных членов:

.

Подставляя в (4) получим:

,

затем: и т.д.

(5).

Итерации прерываются при выполнении условия:

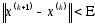, где

- норма вектора, -max .

Теорема (условие сходимости итерационного процесса).

Если сумма модулей элементов строк или сумма модулей элементов столбцов меньше единицы, то процесс итераций для данной системы сходится к единственному решению, независимо от выбора начального приближения, т.е.:

при ,

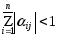или: при.

На практике поступают следующим образом. Из заданной системы А · х = В выделяют уравнения с коэффициентами, модули которых больше или равны сумме модулей остальных коэффициентов уравнения. Каждое выделенное уравнение выписывают в такую строку новой системы, чтобы наибольший по модулю коэффициент оказался диагональным.

Из оставшихся использованных уравнений системы составляют между собой линейные комбинации с таким расчетом, чтобы был соблюден указанный выше принцип комплектования новой системы и все свободные строки оказались заполненными. При этом каждое использованное ранее уравнение должно попасть хотя бы в одну линейную комбинацию, являющуюся уравнением новой системы.

В итоге получаем преобразованную линейную систему, эквивалентную исходной и удовлетворяющей условию сходимости итерационного процесса.