Дискретная математика / Курсовая работа по дискретной математике
.docСодержание.
|
1 |
Оптимальный по порядку метод синтеза схем из Ф. Э. ( метод Шеннона). |
2 |
|
2 |
Расчет курсовой работы |
3 |
|
3 |
Чертеж схемы БИПа |
19 |
|
4 |
Список литература |
10 |
Метод каскадов.
Метод каскадов позволяет минимизировать трудоемкость синтеза логической схемы за счет снижения размерности синтезируемой функции и за счет использования специального структурного модуля – модуля исключения переменной.
В основе метода лежит теорема Шеннона.
Оптимальный по порядку метод синтеза схем из Ф. Э. ( метод Шеннона).
Полученная оценка
показывает, что наилучшие из элементарных
методов синтеза отличаются по порядку
от нижней оценки в n раз.
Это означает, что дальнейшее
совершенствование методов синтеза
может привести к уменьшению верхней
оценки для функции Шеннона по порядку
не более чем в n раз по
сравнению с
.
В действительности оказалось, что
существует такой метод синтеза, который
приводит к верхней оценке для функции
Шеннона, по порядку совпадения с нижней
оценкой. Этот метод был создан К. Шенноном
для контактных схем. Этот метод для
реализации булевых функций схемами из
Ф. Э.
Пусть
- множество булевых функций
.
Определение. Многополюсник из Ф.
Э., имеющий n входов и s
выходов, называется универсальным для
данного множества функции, если для
каждого
в многополюснике найдется выход
такой, что на нем реализуется функция
.
Лемма 4. Для любого n
можно построить универсальный
многополюсник Un
для множества всех булевых функций от
n переменных
,
и
.
Доказательство. Построение
многополюсника
будем
осуществлять индуктивным способом.
Базис индукции
.
В качестве
возьмем многополюсник, изображенный
на рисунке. Имеем
.
Индуктивный переход. Предположим,
что построен универсальный многополюсник
для множества всех булевых функций,
зависящих от переменных
.
Рассмотрим разложение
.
Множество всех булевых функций, зависящих
от переменных
,
разобьем на три непересекающихся класса.
I.
.
Этот класс содержит одну функцию
.
II. Ровно одна из функций f’ или f’’ тождественно равны 0. В этом классе содержатся функции f вида
или
,
т.е.
функций.
-
Все остальные функции, т.е. функции f, у которых
.
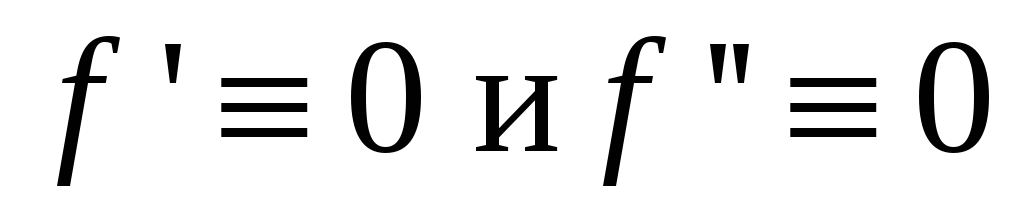В этом классе имеется
функций.
На рисунке 2 изображен многополюсник Un. Здесь выходы многополюсника Un-1 занумерованы числами
,
причем считается, что на выходе 1
реализуется константа 0.
Выходы многополюсника Un
разбиты на три класса в соответствии с
разбиением множества всех булевых
функций, зависящих от переменных
.
Данный многополюсник содержит:
а) подсхему Un-1 и вне нее еще
б) один инвертор,
в)
конъюнкторов,
г)
дизъюнкторов.
Таким образом,
.
Лемма доказана.
Теорема Шеннона: Любая, отличная от тождественного нуля логическая функция f(x1,..,xn) представима в виде
Функции
и
получается
подстановкой в f(x1,..,xn)
вместо переменной
значение
1 и 0 соответственно. Размерность этих
функций на 1 меньше исходной. Функции
и
называют остаточными функциями при
разложении f(x1,..,xn)
по переменной
единичной и нулевой, соответственно. В
дальнейшем, эти функции для краткости
будут называться, как
и
,
соответственно.
В общем виде теорема Шеннона формулируется следующим образом:
по все наборам
.
Это означает, что при разложении функции по k – переменным получаем 2k остаточных функций, каждая из которых зависит от n-k переменных.
Следствие из теоремы Шеннона: Предельное разложение функции по n-переменным является совершенная дизъюнктивная нормальная форма (СовДНФ).
Действительно, разложение Шеннона будет представлена дизъюнкцией конституент, каждая из которых конъюнктивно связана с остаточной функцией – константой. Функция константа принимает, имеет значение1, если соответствующая ей конституента является единичной, и 0 – в противном случае.
Для краткости разложение Шеннона по
одной переменной представляется как
.
Если предположить, что имеется
конструктивный блок, реализующий это
представление (блок исключения переменной
– БИП), его внутреннею структура в
классическом базисе должна иметь
следующий вид:
Расчет курсовой работы.
Задание к курсовой работе по дискретной математике «метод каскадов».
Базис Шеффера.
Решение задачи.
1. Определяем, какую переменную следует исключить первой
Значения производной вычислим по таблице
|
|
|
|||
|
|
00 |
01 |
10 |
11 |
|
00 |
0 |
0 |
1 |
1 |
|
01 |
1 |
1 |
1 |
0 |
|
10 |
0 |
0 |
0 |
0 |
|
11 |
0 |
0 |
0 |
0 |
Таким образом вес производной
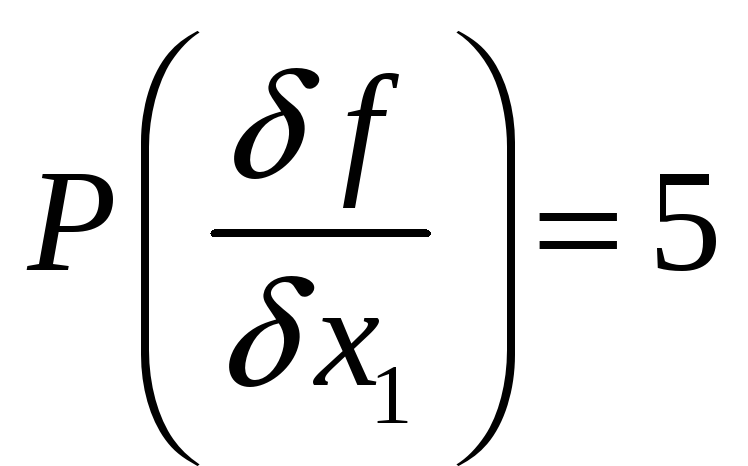
Значение производной вычислим по таблице
|
|
|
|||
|
|
00 |
01 |
10 |
11 |
|
00 |
1 |
0 |
0 |
0 |
|
01 |
0 |
0 |
1 |
0 |
|
10 |
1 |
0 |
1 |
1 |
|
11 |
1 |
1 |
0 |
0 |
Таким образом вес производной
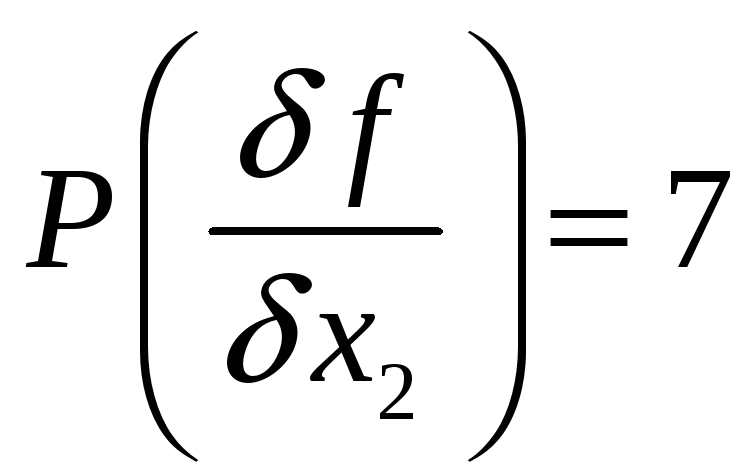
Значение производной вычислим по таблице
|
|
|
|||
|
|
00 |
01 |
10 |
11 |
|
00 |
1 |
1 |
1 |
0 |
|
01 |
0 |
1 |
0 |
0 |
|
10 |
1 |
0 |
1 |
1 |
|
11 |
0 |
1 |
0 |
0 |
Таким образом вес производной
Значения производной вычислим по таблице
|
|
|
|||
|
|
00 |
01 |
10 |
11 |
|
00 |
0 |
0 |
0 |
1 |
|
01 |
1 |
0 |
1 |
1 |
|
10 |
1 |
1 |
0 |
0 |
|
11 |
1 |
0 |
1 |
1 |
Таким образом веем производной
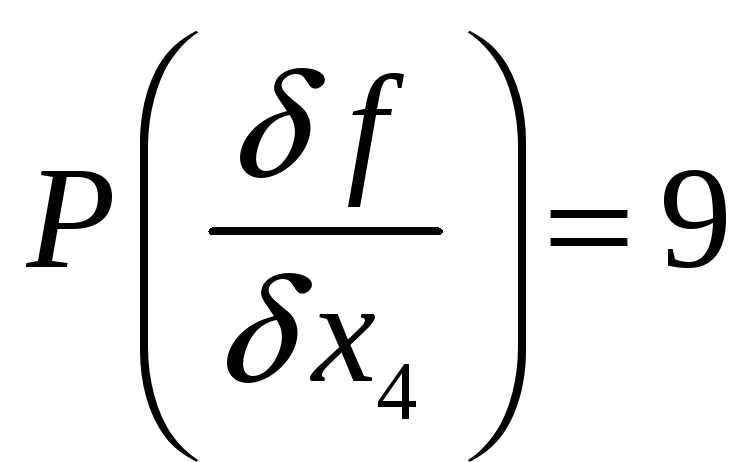
Значение производной вычисляем по таблице
|
|
|
|||
|
|
00 |
01 |
10 |
11 |
|
00 |
0 |
0 |
0 |
1 |
|
01 |
1 |
0 |
0 |
0 |
|
10 |
0 |
0 |
0 |
0 |
|
11 |
1 |
0 |
0 |
0 |
Таким образом вес производной
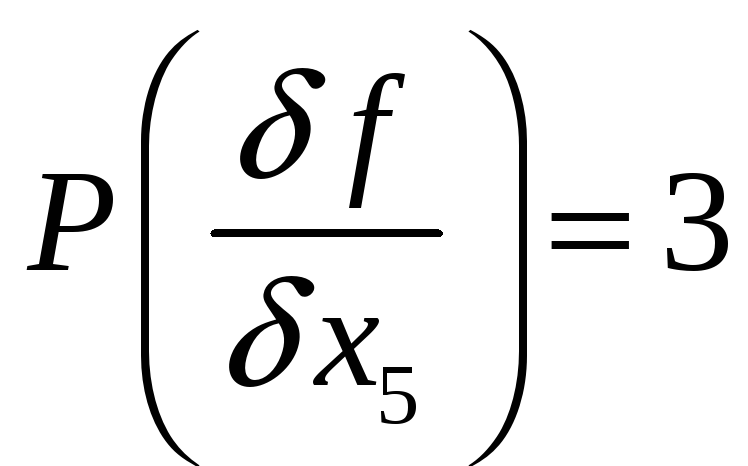
Как следует из проведенных расчетов производных, первой следует исключить переменную x4.
Нулевая остаточная функция
зависит от четырех переменных. Для
этого необходимо выделить переменную,
которая должна быть исключена первой.
Так же необходимо выделить переменную,
которая будет исключена первой в
единичной остаточной функции
.
Для этого необходимо вычислить веса
производных по
нулевая остаточная функция.
единичная остаточная функция.
Вычислим значение производной по таблице от нулевой остаточной функции
|
|
|
|||
|
|
00 |
01 |
10 |
11 |
|
0 |
0 |
0 |
0 |
0 |
|
1 |
0 |
0 |
0 |
0 |
Таким образом вес производной
Вычислим значение производной по таблице от нулевой остаточной функции
|
|
|
|||
|
|
00 |
01 |
10 |
11 |
|
0 |
1 |
0 |
1 |
0 |
|
1 |
0 |
0 |
1 |
1 |
Таким образом вес производной
Вычислим значение производной по таблице от нулевой остаточной функции
|
|
|
|||
|
|
00 |
01 |
10 |
11 |
|
0 |
1 |
0 |
1 |
0 |
|
1 |
1 |
1 |
0 |
1 |
Таким образом вес производной
Вычислим значение производной по таблице от нулевой остаточной функции
|
|
|
|||
|
|
00 |
01 |
10 |
11 |
|
0 |
0 |
0 |
1 |
0 |
|
1 |
0 |
0 |
1 |
0 |
Таким образом вес производной
Как следует из проведенных расчетов производных нулевой остаточной функции, первой следует исключить переменную x2.
Теперь остаточная функция зависит от двух переменных и для завершения схемы в заданном базис необходимо синтезировать остаточные функции в заданном базисе и показать структуру БИПа в заданном базисе.
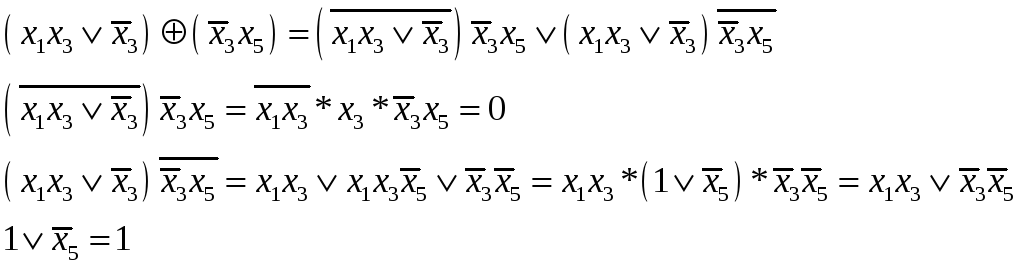
Вычислим значение производной по таблице от нулевой остаточной функции
|
|
|
|||
|
|
00 |
01 |
10 |
11 |
|
0 |
1 |
1 |
1 |
0 |
|
1 |
0 |
0 |
0 |
0 |
Таким образом вес производной
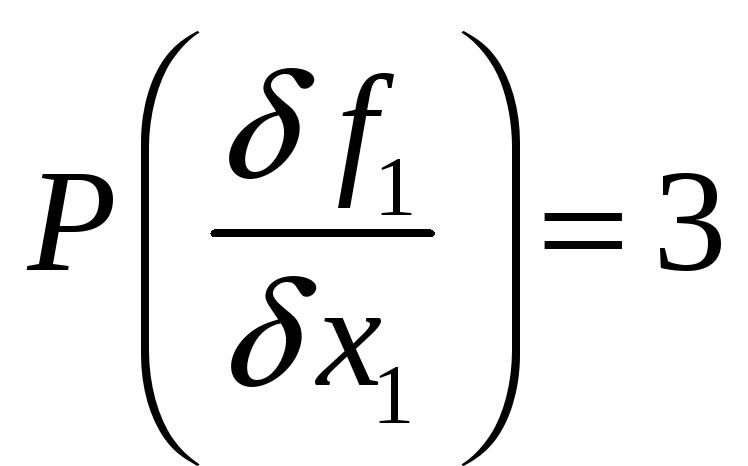
Вычислим значение производной по таблице от нулевой остаточной функции
|
|
|
|||
|
|
00 |
01 |
10 |
11 |
|
0 |
0 |
0 |
1 |
1 |
|
1 |
1 |
1 |
0 |
0 |
Таким образом вес производной
Вычислим значение производной по таблице от нулевой остаточной функции
|
|
|
|||
|
|
00 |
01 |
10 |
11 |
|
0 |
1 |
0 |
1 |
0 |
|
1 |
0 |
0 |
1 |
0 |
Таким образом вес производной
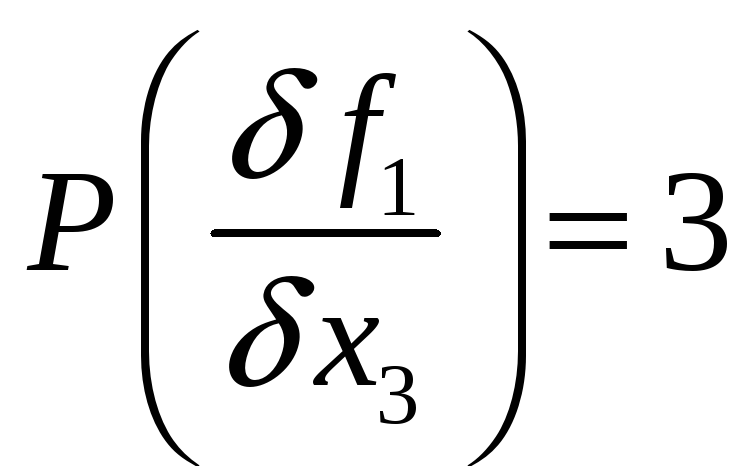
Вычислим значение производной по таблице от нулевой остаточной функции
|
|
|
|||
|
|
00 |
01 |
10 |
11 |
|
0 |
0 |
1 |
0 |
0 |
|
1 |
0 |
0 |
0 |
0 |
Таким образом вес производной
Как следует из проведенных расчетов производных единичной остаточной функции, первой следует исключить переменную x2.
(
)
остаточная функция от единичной
остаточной функции и зависит от трех
переменных. Для этого нужно выделить
переменную, которая будет исключена
первой из f10.
Так же необходимо выделить переменную,
которая будет исключена из остаточной
функции (f11). Для
этого необходимо найти веса производной
от
.
Вычислим значения производной от функции f10
Таким образом вес производной
Вычислим значения производной от функции f10
Таким образом вес производной
Таким образом вес производной
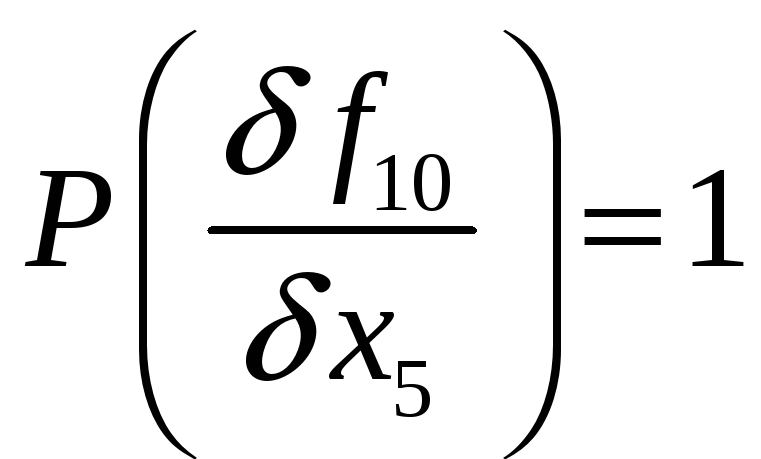
Как следует из проведенных расчетов производных, первой следует исключить либо переменную х1 или х3. Для построения схемы принимаем «волевое» решение об исключении переменной х1.
Теперь остаточные функции зависят не более чем от двух переменных и для завершения схемы в заданном базис необходимо синтезировать остаточные функции в базисе и показать структуру БИПа в заданном базисе.
Вычислим значение производной от функции f11
Таким образом вес производной
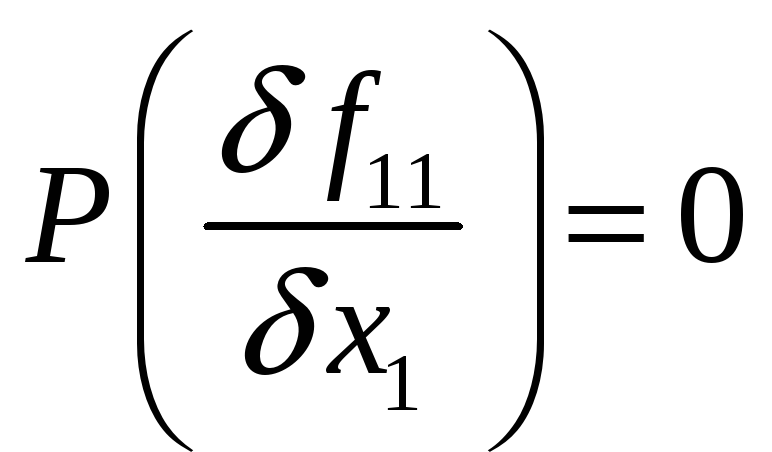
Вычислим значение производной от функции f11
Таким образом вес производной
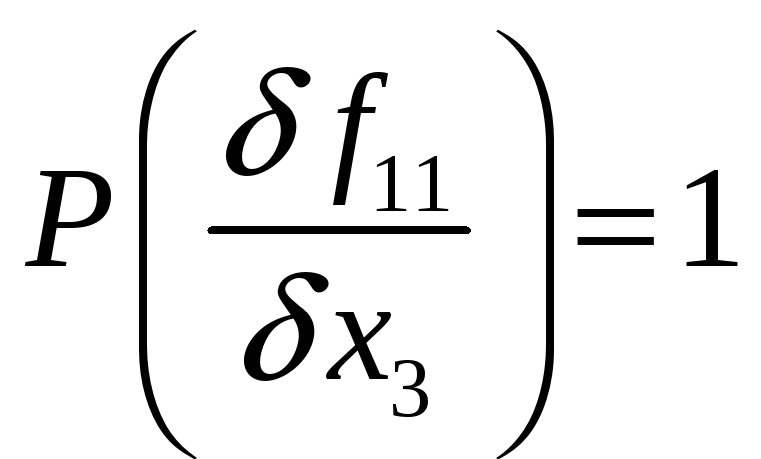
Вычислим значение производной от функции f11
Таким образом вес производной
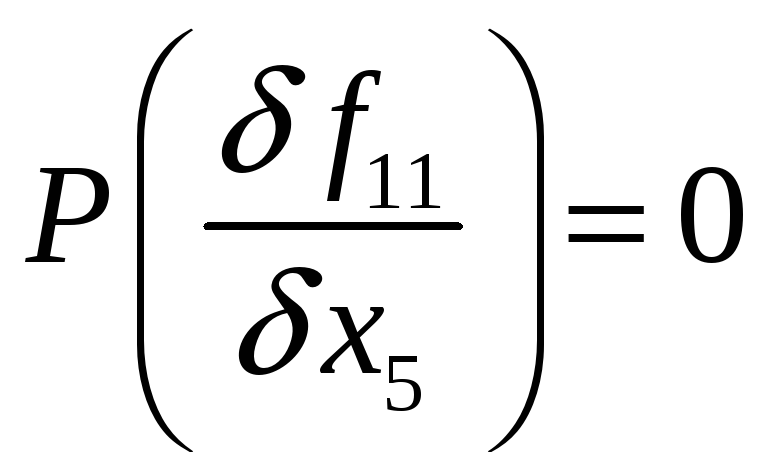
Как следует из проведенных расчетов производных, первой следует исключить либо переменную х3.
Теперь остаточные функции зависят не более чем от двух переменных и для завершения схемы в заданном базис необходимо синтезировать остаточные функции в базисе и показать структуру БИПа в заданном базисе.
